2020-2021学年安徽省安庆市潜山县九年级(上)期末数学试卷(Word版含解析)
文档属性
| 名称 | 2020-2021学年安徽省安庆市潜山县九年级(上)期末数学试卷(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览

文档简介
2020-2021学年安徽省安庆市潜山县九年级第一学期期末数学试卷
一、选择题(共10小题,每题4分,共40分).
1.已知=,则的值为( )
A.
B.
C.1
D.
2.在△ABC中,∠C=90°,tanA=2,则cosA的值为( )
A.
B.
C.
D.2
3.如图,⊙O是△ABC的外接圆,已知∠OAB=25°,则∠ACB的大小为( )
A.55°
B.65°
C.50°
D.60°
4.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
A.
B.
C.
D.
5.在函数y=﹣x2+bx+c中,y与x的部分对应值如表,则m、n的大小关系为( )
x
……
﹣1
1
3
4
……
y
……
﹣6
m
n
﹣6
……
A.m>n
B.m<n
C.m=n
D.无法确定
6.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A.
B.
C.
D.
7.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A.
B.
C.
D.
8.已知直线y=kx(k>0,k是常数)与双曲线y=交于点A(x1,y1),B(x2,y2)两点,则2x1y2﹣x2y1的值为( )
A.5
B.0
C.﹣5
D.﹣10
9.如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线x=﹣1,有三个结论,其中正确的个数是( )
①ab>0;
②a+b+c>0;
③当x<﹣2时,y<0.
A.0个
B.1个
C.2个
D.3个
10.为庆祝国庆,某公司要在如图所示的五角星中(图中所有线段的长度均相等,且∠A=∠B=∠C=∠D=∠E=36°),从顶点A开始,沿边每隔25厘米装一盏闪光灯,如果F、J两点间的距离等于(﹣1)米,则需要安装闪光灯的盏数是( )(参考数据:sin18°=)
A.70
B.80
C.79
D.71
二、填空题(本大题共4小题,每小题5分,满分20分。请把你的答案填写在Ⅱ卷对应题号下的横线上。)
11.如图,已知点A在反比例函数y=(k是常数,x<0)的图象上,过点A作AB⊥y轴于B,若△AOB的面积为1,则k的值是
.
12.△ABC中,AB=9cm,AC=40cm,BC=41cm,则△ABC的外接圆半径长是
.
13.如图,AB是⊙O的直径,点C在⊙O上,AB=8,∠CAB=20°,D是弧BC的中点,P是直径AB上的一动点,则PC+PD的最小值为
.
14.对于两个不相等的实数a、b,我们规定符号min{a,b}表示a、b中的较小值,如:min{1,2}=1,按照这个规定,方程min{x,﹣x}=的解为
.
三、解答题(本大题共9小题,共90分)解答应写明文字说明和运算步骤.
15.计算:sin245°+cos30°sin30°﹣tan60°.
16.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使=,并写出点A2的坐标.
17.如图,在锐角三角形OAB中,点C,D分别在边OA,OB上,OG⊥AB于点G,OH⊥CD于点H,∠COH=∠GOB.
(1)求证:△ODC∽△OAB;
(2)若OD=3,OA=7,求的值.
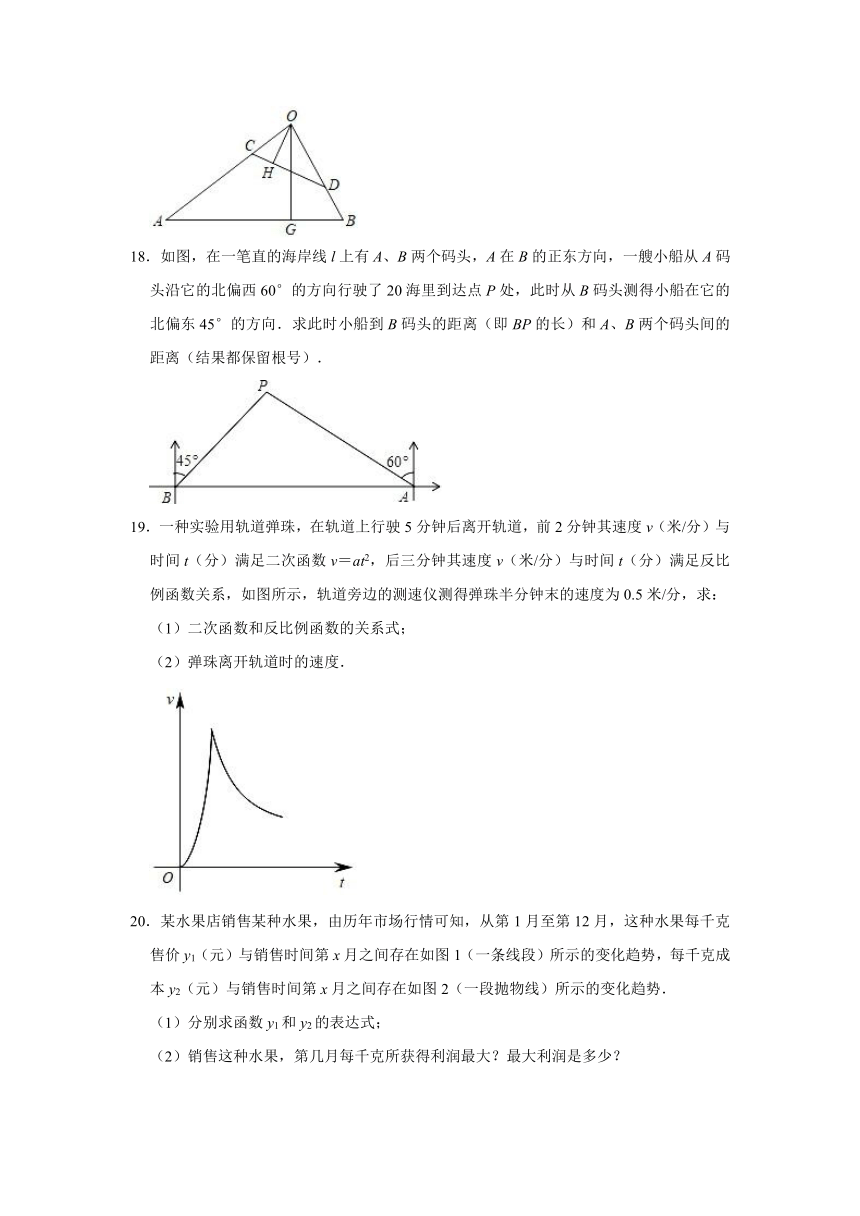
18.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
19.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图所示,轨道旁边的测速仪测得弹珠半分钟末的速度为0.5米/分,求:
(1)二次函数和反比例函数的关系式;
(2)弹珠离开轨道时的速度.
20.某水果店销售某种水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)所示的变化趋势,每千克成本y2(元)与销售时间第x月之间存在如图2(一段抛物线)所示的变化趋势.
(1)分别求函数y1和y2的表达式;
(2)销售这种水果,第几月每千克所获得利润最大?最大利润是多少?
21.如图,AB是⊙O的直径,C、G是⊙O上两点,且=,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若=,求∠E的度数;
(3)在(2)的条件下,若CD=cm,求⊙O的直径AB的长.
22.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,点D在边BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式.
23.如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,﹣),且与x轴交于A、B两点(点A在点B的右侧),与y轴交于C点,点C的坐标为(0,﹣4),P是抛物线上的一个动点,且横坐标为m.
(1)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求点P的横坐标m的取值范围;
(3)当m<0时,过点P作y轴的垂线PQ,垂足为Q.问:是否存在点P,使∠QPO=∠BCO?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题(共10小题,每题4分,共40分).
1.已知=,则的值为( )
A.
B.
C.1
D.
【分析】根据已知条件求出a=2b,再代入求出答案即可.
解:∵=,
∴a=2b,
∴
=
=
=,
故选:D.
2.在△ABC中,∠C=90°,tanA=2,则cosA的值为( )
A.
B.
C.
D.2
【分析】根据锐角三角函数的定义和勾股定理求解即可.
解:在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA=2=,不妨设b=k,则a=2k,由勾股定理得,c==k,
所以cosA===,
故选:A.
3.如图,⊙O是△ABC的外接圆,已知∠OAB=25°,则∠ACB的大小为( )
A.55°
B.65°
C.50°
D.60°
【分析】由OA=OB,可求得∠OBA=∠OAB=25°,继而求得∠AOB的度数,然后由圆周角定理,求得答案.
解:∵OA=OB,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∴∠ACB=∠AOB=65°.
故选:B.
4.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
A.
B.
C.
D.
【分析】根据题意得出△ADE∽△ABC,进而利用已知得出对应边的比值.
解:∵DE∥BC,
∴△ADE∽△ABC,
∵BD=2AD,
∴===,
则=,
∴A,C,D选项错误,B选项正确,
故选:B.
5.在函数y=﹣x2+bx+c中,y与x的部分对应值如表,则m、n的大小关系为( )
x
……
﹣1
1
3
4
……
y
……
﹣6
m
n
﹣6
……
A.m>n
B.m<n
C.m=n
D.无法确定
【分析】首先确定抛物线的对称轴,然后根据抛物线的对称性求解.
解:∵抛物线经过点(﹣1,﹣6)和(4,﹣6),
∴抛物线的对称轴为=,
∴点(1,m)到对称轴的距离小于点(3,n)到对称轴的距离,
∵a=﹣1<0,
∴抛物线开口向下,
∴m>n,
故选:A.
6.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A.
B.
C.
D.
【分析】本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.
解:∵函数y=的图象经过二、四象限,∴k<0,
∴抛物线开口向下,对称轴x=﹣=<0,
即对称轴在y轴的左边.
故选:D.
7.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A.
B.
C.
D.
【分析】由图可得∠ACB=135°,AC=,BC=2,然后分别求得A,B,C,D中各三角形的最大角,继而求得答案.
解:如图:∠ACB=135°,AC=,BC=2,
A、最大角=135°,对应两边分别为:1,,
∵:1=2:,
∴此图与△ABC相似;
B、∵最大角<135°,
∴与△ABC不相似;
C、∵最大角<135°,
∴与△ABC不相似;
D、∵最大角<135°,
∴与△ABC不相似.
故选:A.
8.已知直线y=kx(k>0,k是常数)与双曲线y=交于点A(x1,y1),B(x2,y2)两点,则2x1y2﹣x2y1的值为( )
A.5
B.0
C.﹣5
D.﹣10
【分析】由于正比例函数和反比例函数图象都是以原点为中心的中心对称图形,因此它们的交点A、B关于原点成中心对称,则有x2=﹣x1,y2=﹣y1.由A(x1,y1)在双曲线y=上可得x1?y1=5,然后把x2=﹣x1,y2=﹣y1代入2x1y2﹣x2y1的就可解决问题.
解:∵直线y=kx(k>0)与双曲线y=都是以原点为中心的中心对称图形,
∴它们的交点A、B关于原点成中心对称,
∴x2=﹣x1,y2=﹣y1.
∵A(x1,y1)在双曲线y=上,
∴x1?y1=5,
∴2x1y2﹣x2y1=2x1?(﹣y1)﹣(﹣x1)?y1=﹣x1?y1=﹣5.
故选:C.
9.如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线x=﹣1,有三个结论,其中正确的个数是( )
①ab>0;
②a+b+c>0;
③当x<﹣2时,y<0.
A.0个
B.1个
C.2个
D.3个
【分析】由抛物线的开口向上,对称轴在y轴左侧,判断a,b与0的关系,得到ab>0,即可判断①;由x=1时,得到y=a+b+c>0,即可判断②;根据对称轴和抛物线与x轴的一个交点,得到另一个交点,然后根据图象即可判断③.
解:①∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴的左侧,
∴b>0
∴ab>0,故①正确;
②∵观察图象知;当x=1时y=a+b+c>0,
故②正确;
③∵抛物线的对称轴为x=﹣1,与x轴交于(0,0),
∴另一个交点为(﹣2,0),
∴当x<﹣2时,y>0,故③错误;
故选:C.
10.为庆祝国庆,某公司要在如图所示的五角星中(图中所有线段的长度均相等,且∠A=∠B=∠C=∠D=∠E=36°),从顶点A开始,沿边每隔25厘米装一盏闪光灯,如果F、J两点间的距离等于(﹣1)米,则需要安装闪光灯的盏数是( )(参考数据:sin18°=)
A.70
B.80
C.79
D.71
【分析】本题需要求出五角星的边长,即求出AF的长.由于五角星是由正五边形各边的延长线相交所得,可得∠A的度数.在等腰△FJ中,根据BC的长和∠ABC的度数,可求出AB的长.即可求出五角星的周长,由此可求出需安装闪光灯的数量.
解:如图:连接FJ,作AM⊥FJ于点M,
∵∠FAJ=∠B=∠C=∠D=∠E=36°,
∴∠FAM=18°,FM=FJ=,
∵sin18°=,
∴=AF,
∴AF=2(米),
∴AF+AJ+JE+EI+ID+DH+HC+CG+BG+BF=2000cm,
则需安装闪光灯:2000÷25=80(盏).
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分。请把你的答案填写在Ⅱ卷对应题号下的横线上。)
11.如图,已知点A在反比例函数y=(k是常数,x<0)的图象上,过点A作AB⊥y轴于B,若△AOB的面积为1,则k的值是 ﹣2 .
【分析】根据△AOB的面积确定k的绝对值为2,再由点A所在象限确定k为﹣2.
解:设点A的坐标为(x,y),且xy=k.
∵点A在第二象限,
∴x<0,y>0.
AB=﹣x,OB=y.
∴S△AOB=AB×OB
=.
∴xy=k=﹣2.
故答案为:﹣2.
12.△ABC中,AB=9cm,AC=40cm,BC=41cm,则△ABC的外接圆半径长是 20.5cm .
【分析】由在△ABC中,AB=9cm,AC=40cm,BC=41cm,可判定△ABC是直角三角形,然后由直角三角形的斜边即是它的外接圆的直径,求得答案.
解:在△ABC中,AB=9cm,AC=40cm,BC=41cm,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,且AB是斜边,
∴△ABC的外接圆半径长为:AB=20.5cm.
故答案为:20.5cm.
13.如图,AB是⊙O的直径,点C在⊙O上,AB=8,∠CAB=20°,D是弧BC的中点,P是直径AB上的一动点,则PC+PD的最小值为 4 .
【分析】作D点关于AB的对称点E,如图,利用对称的性质得到PE=PD,=,再根据两点之间线段最短判断PC+PD的值最小,接着根据圆周角定理得到∠BOC=40°,∠BOE=20°,然后通过证明△COE为等边三角形得到CE的长即可.
解:作D点关于AB的对称点E,连接CE交AB于P,如图,
∵点D与点E关于AB对称,
∴PE=PD,=,
∴PC+PD=PC+PE=CE,
∴此时点P点即为PC+PD的值最小的点,最小值为CE的长度,
∵∠BOC=2∠CAB=2×20°=40°,
而D为弧BC的中点,
∴∠BOE=∠BOC=20°,
∴∠COE=40°+20°=60°,
∴△COE为等边三角形,
∴CE=OC=AB=4,
∴PC+PD的最小值为4.
故答案为:4.
14.对于两个不相等的实数a、b,我们规定符号min{a,b}表示a、b中的较小值,如:min{1,2}=1,按照这个规定,方程min{x,﹣x}=的解为 1﹣ .
【分析】分类讨论x与﹣x的大小,分别求出方程的解,检验即可.
解:当x>﹣x,即x>0时,方程变形得:﹣x=,
整理得:x2+2x+1=0,即(x+1)2=0,
解得:x1=x2=﹣1,不符合题意,舍去;
当x<﹣x,即x<0时,方程变形得:x=,
方程整理得:x2﹣2x=1,即(x﹣1)2=2,
解得:x1=1+(不符合题意,舍去),x2=1﹣,
经检验x=1﹣是分式方程的解,
综上,方程的解为x=1﹣.
三、解答题(本大题共9小题,共90分)解答应写明文字说明和运算步骤.
15.计算:sin245°+cos30°sin30°﹣tan60°.
【分析】直接利用特殊角的三角函数值以及二次根式的性质计算得出答案.
解:原式=×()2+×﹣
=×+﹣
=﹣.
16.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使=,并写出点A2的坐标.
【分析】(1)利用关于x轴对称的点的坐标特征,写出A1、B1、C1的坐标,然后描点即可得到△A
1B1C1;
(2)把A、B、C的横纵坐标后乘以﹣2得到出A2、B2、C2的坐标,然后描点即可得到△A
2B2C2.
解:(1)如图,△A
1B1C1为所作,A1(1,﹣3);
(2)如图,△A2B2C2为所作,A2(﹣2,﹣6).
17.如图,在锐角三角形OAB中,点C,D分别在边OA,OB上,OG⊥AB于点G,OH⊥CD于点H,∠COH=∠GOB.
(1)求证:△ODC∽△OAB;
(2)若OD=3,OA=7,求的值.
【分析】(1)根据垂线的性质得到∠OHC=∠OGB=90°,结合题意∠COH=∠GOB,从而推出△OHC∽OGB,根据相似三角形的性质得到∠OCH=∠B,结合图形中的公共角∠DOC=∠AOB,利用相似三角形的判定定理证明即可;
(2)根据(1)中的结论△ODC∽△OAB,从而利用根据相似三角形的性质进行求解即可.
【解答】(1)证明:∵OG⊥AB于点G,OH⊥CD于点H,
∴∠OHC=∠OGB=90°,
又∠COH=∠GOB,
∴△OHC∽OGB,
∴∠OCH=∠B,
∵∠DOC=∠AOB,
∴△ODC∽△OAB;
(2)由(1)得△ODC∽△OAB,
∴=,
又OD=3,OA=7,
∴=.
18.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
【分析】过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、BP.
解:如图:
过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20海里,
∴PM=AP=10海里,AM=cos30°AP=10海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10)海里,
∴BP==10海里,
即小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里.
19.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图所示,轨道旁边的测速仪测得弹珠半分钟末的速度为0.5米/分,求:
(1)二次函数和反比例函数的关系式;
(2)弹珠离开轨道时的速度.
【分析】(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=5代入(1)中反比例函数的解析式即可.
解:(1)v=at2的图象经过点(,),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=(2<t≤5);
(2)由图象知,弹珠在第5分钟末离开轨道,速度为=3.2(米/分).
20.某水果店销售某种水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)所示的变化趋势,每千克成本y2(元)与销售时间第x月之间存在如图2(一段抛物线)所示的变化趋势.
(1)分别求函数y1和y2的表达式;
(2)销售这种水果,第几月每千克所获得利润最大?最大利润是多少?
【分析】(1)设y1=kx+b(k≠0),y2=a(x﹣5)2+8,用待定系数法求解即可;
(2)设第x月每千克所获得的利润为w(元),由题意得w关于x的二次函数,根据二次函数的性质可得答案.
解:(1)由题意设y1=kx+b(k≠0),y2=a(x﹣5)2+8,
将(6,10),(9,9)代入y1=kx+b,得:
,
解得,
∴y1=﹣x+12;
将(11,14)代入y2=a(x﹣5)2+8,得:
14=a(11﹣5)2+8,
解得a=,
∴y2=(x﹣5)2+8,
函数y1和y2的表达式分别为y1=﹣x+12,y2=(x﹣5)2+8;
(2)设第x月每千克所获得的利润为w(元),由题意得:
w=﹣x+12﹣[(x﹣5)2+8]
=﹣(x﹣4)2+2.5,
∴当x=4时,w有最大值,w最大=2.5.
∴销售这种水果,第4个月每千克所获得利润最大,最大利润是2.5元.
21.如图,AB是⊙O的直径,C、G是⊙O上两点,且=,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若=,求∠E的度数;
(3)在(2)的条件下,若CD=cm,求⊙O的直径AB的长.
【分析】(1)要证明CD是⊙O的切线,连接OC,只要证明∠OCE=90°即可,根据题目中的条件,可以证明OC∥BD,再根据CD⊥BG于点D,从而可以证明结论成立;
(2)由(1)知,OC∥BD,则△COF∽△BDF,即可得出==,进而得出==,继而得到EO=2OB=2OC,即可得解;
(3)由(2)知∠E=30°,可得∠EBD=60°,∠CBD=30°,继而得出BC=2CD=2cm,BD==3cm,再根据=,即可求出OC,进而求出AB.
【解答】(1)证明:连接OC,
∵OC=OB,=,
∴∠OCB=∠OBC,∠OBC=∠CBD,
∴∠CBD=∠OCB,
∴OC∥BD,
∴∠ECO=∠EDB,
∵CD⊥BG于点D,
∴∠EDB=90°,
∴∠ECO=90°,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)解:由(1)知,OC∥BD,
∴△COF∽△BDF,
∴=,
∵=,
∴=,
∴==,
∴EO=2OB=2OC,
∵∠CEO=90°,
∴∠E=30°;
(3)解:由(2)知,∠E=30°,
∴∠EBD=60°,
∴∠CBD=30°,
∵∠BDE=90°,CD=cm,
∴BC=2CD=2cm,
∴BD==3cm,
由(2)知,=,
∴OC=2cm,
∴AB=4(cm),
答:⊙O的直径AB的长是4cm.
22.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,点D在边BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式.
【分析】(1)由ED=EB得到∠B=∠DEB,再根据等角的余角相等得到∠A=∠FEG,加上公共角∠G,则可判断△EFG∽△AEG;
(2)过E点作EH⊥AC于H,如图,先证明△AEF∽△ACB得到==,再利用△EFG∽△AEG得到===,则EG=2x,GA=4x,AF=3x,在Rt△AEF中利用勾股定理可求出EF=x,AE=x,接着利用面积法求出EH=x,然后根据三角形面积公式得到y关于x的函数解析式.
【解答】(1)证明:∵ED=EB,
∴∠B=∠DEB,
∵∠ACB=90°,
∴∠A+∠B=90°,
∵EF⊥AB,
∴∠FBE=90°,
∴∠DEB+∠FEG=90°,
∴∠A=∠FEG,
∵∠EGF=∠AGE,
∴△EFG∽△AEG;
(2)解:过E点作EH⊥AC于H,如图,
∵∠AEF=∠ACB,∠EAF=∠CAB,
∴△AEF∽△ACB,
∴=,
∴===,
∵△EFG∽△AEG,
∴===,
∵FG=x,
∴EG=2x,GA=4x,
∴AF=3x,
在Rt△AEF中,∵EF2+AE2=AF2,
∴EF2+4EF2=(3x)2,解得EF=x,
∴AE=x,
∵EH?AF=EF?AE,
∴EH==x,
∴△EFG的面积=?FG?EH=?x?x=x2,
即y关于x的函数解析式为y=x2.
23.如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,﹣),且与x轴交于A、B两点(点A在点B的右侧),与y轴交于C点,点C的坐标为(0,﹣4),P是抛物线上的一个动点,且横坐标为m.
(1)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求点P的横坐标m的取值范围;
(3)当m<0时,过点P作y轴的垂线PQ,垂足为Q.问:是否存在点P,使∠QPO=∠BCO?若存在,请求出点P的坐标;若不存在,请说明理由.
【分析】(1)根据顶点D的坐标为(1,﹣),可设抛物线表达式为:y=a(x﹣1)2﹣,将C(0,﹣4)代入,即可得抛物线表达式为:y=x2﹣x﹣4;
(2)若∠PAO=45°,过P作PG⊥x轴于G,①可证明△AOC是等腰直角三角形,故∠CAO=45°,若动点P满足∠PAO不大于45°,则m≤0,②△PAG是等腰直角三角形,可得m2﹣m﹣4=4﹣m,解得m=4(舍去)或m=﹣4,若动点P满足∠PAO不大于45°,则m≥﹣4;故可得答案:﹣4≤m≤0;
(3)①当P在第二象限,由∠QPO=∠BCO,∠PQO=∠BOC,得△PQO∽△COB,故=,即=,可得P(,);
②当P在第三象限,同理可得P(,).
解:(1)根据题意设抛物线表达式为:y=a(x﹣1)2﹣,
将C(0,﹣4)代入得:a﹣=﹣4,
∴a=,
∴抛物线表达式为:y=(x﹣1)2﹣=x2﹣x﹣4;
(2)若∠PAO=45°,过P作PG⊥x轴于G,如图:
①在y=x2﹣x﹣4中,令y=0,得x2﹣x﹣4=0,
解得x=﹣2或x=4,
∴A(4,0),B(﹣2,0),
在y=x2﹣x﹣4中,令x=0,得y=4,
∴C(0,4),
∴OA=OC,
∴△AOC是等腰直角三角形,
∴∠CAO=45°,
若动点P满足∠PAO不大于45°,则m≤0,
②∵∠PAO=45°,
∴△PAG是等腰直角三角形,
∴PG=AG,
而P(m,m2﹣m﹣4),
∴m2﹣m﹣4=4﹣m,
解得m=4(舍去)或m=﹣4,
∴若动点P满足∠PAO不大于45°,则m≥﹣4;
由①②可得:﹣4≤m≤0;
(3)存在,理由如下:
①当P在第二象限,如图:
∵∠QPO=∠BCO,∠PQO=∠BOC,
∴△PQO∽△COB,
∴=,
∵B(﹣2,0),C(0,4),P(m,m2﹣m﹣4),
∴=,
解得m=(舍去)或m=,
∴P(,);
②当P在第三象限,如图:
同①可得△POQ∽△CBO,
∴=,即=,
解得m=(舍去)或m=,
∴P(,),
综上所述,当∠QPO=∠BCO时,P的坐标为:(,)或(,).
一、选择题(共10小题,每题4分,共40分).
1.已知=,则的值为( )
A.
B.
C.1
D.
2.在△ABC中,∠C=90°,tanA=2,则cosA的值为( )
A.
B.
C.
D.2
3.如图,⊙O是△ABC的外接圆,已知∠OAB=25°,则∠ACB的大小为( )
A.55°
B.65°
C.50°
D.60°
4.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
A.
B.
C.
D.
5.在函数y=﹣x2+bx+c中,y与x的部分对应值如表,则m、n的大小关系为( )
x
……
﹣1
1
3
4
……
y
……
﹣6
m
n
﹣6
……
A.m>n
B.m<n
C.m=n
D.无法确定
6.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A.
B.
C.
D.
7.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A.
B.
C.
D.
8.已知直线y=kx(k>0,k是常数)与双曲线y=交于点A(x1,y1),B(x2,y2)两点,则2x1y2﹣x2y1的值为( )
A.5
B.0
C.﹣5
D.﹣10
9.如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线x=﹣1,有三个结论,其中正确的个数是( )
①ab>0;
②a+b+c>0;
③当x<﹣2时,y<0.
A.0个
B.1个
C.2个
D.3个
10.为庆祝国庆,某公司要在如图所示的五角星中(图中所有线段的长度均相等,且∠A=∠B=∠C=∠D=∠E=36°),从顶点A开始,沿边每隔25厘米装一盏闪光灯,如果F、J两点间的距离等于(﹣1)米,则需要安装闪光灯的盏数是( )(参考数据:sin18°=)
A.70
B.80
C.79
D.71
二、填空题(本大题共4小题,每小题5分,满分20分。请把你的答案填写在Ⅱ卷对应题号下的横线上。)
11.如图,已知点A在反比例函数y=(k是常数,x<0)的图象上,过点A作AB⊥y轴于B,若△AOB的面积为1,则k的值是
.
12.△ABC中,AB=9cm,AC=40cm,BC=41cm,则△ABC的外接圆半径长是
.
13.如图,AB是⊙O的直径,点C在⊙O上,AB=8,∠CAB=20°,D是弧BC的中点,P是直径AB上的一动点,则PC+PD的最小值为
.
14.对于两个不相等的实数a、b,我们规定符号min{a,b}表示a、b中的较小值,如:min{1,2}=1,按照这个规定,方程min{x,﹣x}=的解为
.
三、解答题(本大题共9小题,共90分)解答应写明文字说明和运算步骤.
15.计算:sin245°+cos30°sin30°﹣tan60°.
16.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使=,并写出点A2的坐标.
17.如图,在锐角三角形OAB中,点C,D分别在边OA,OB上,OG⊥AB于点G,OH⊥CD于点H,∠COH=∠GOB.
(1)求证:△ODC∽△OAB;
(2)若OD=3,OA=7,求的值.
18.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
19.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图所示,轨道旁边的测速仪测得弹珠半分钟末的速度为0.5米/分,求:
(1)二次函数和反比例函数的关系式;
(2)弹珠离开轨道时的速度.
20.某水果店销售某种水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)所示的变化趋势,每千克成本y2(元)与销售时间第x月之间存在如图2(一段抛物线)所示的变化趋势.
(1)分别求函数y1和y2的表达式;
(2)销售这种水果,第几月每千克所获得利润最大?最大利润是多少?
21.如图,AB是⊙O的直径,C、G是⊙O上两点,且=,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若=,求∠E的度数;
(3)在(2)的条件下,若CD=cm,求⊙O的直径AB的长.
22.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,点D在边BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式.
23.如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,﹣),且与x轴交于A、B两点(点A在点B的右侧),与y轴交于C点,点C的坐标为(0,﹣4),P是抛物线上的一个动点,且横坐标为m.
(1)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求点P的横坐标m的取值范围;
(3)当m<0时,过点P作y轴的垂线PQ,垂足为Q.问:是否存在点P,使∠QPO=∠BCO?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题(共10小题,每题4分,共40分).
1.已知=,则的值为( )
A.
B.
C.1
D.
【分析】根据已知条件求出a=2b,再代入求出答案即可.
解:∵=,
∴a=2b,
∴
=
=
=,
故选:D.
2.在△ABC中,∠C=90°,tanA=2,则cosA的值为( )
A.
B.
C.
D.2
【分析】根据锐角三角函数的定义和勾股定理求解即可.
解:在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,
由于tanA=2=,不妨设b=k,则a=2k,由勾股定理得,c==k,
所以cosA===,
故选:A.
3.如图,⊙O是△ABC的外接圆,已知∠OAB=25°,则∠ACB的大小为( )
A.55°
B.65°
C.50°
D.60°
【分析】由OA=OB,可求得∠OBA=∠OAB=25°,继而求得∠AOB的度数,然后由圆周角定理,求得答案.
解:∵OA=OB,
∴∠OBA=∠OAB=25°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=130°,
∴∠ACB=∠AOB=65°.
故选:B.
4.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
A.
B.
C.
D.
【分析】根据题意得出△ADE∽△ABC,进而利用已知得出对应边的比值.
解:∵DE∥BC,
∴△ADE∽△ABC,
∵BD=2AD,
∴===,
则=,
∴A,C,D选项错误,B选项正确,
故选:B.
5.在函数y=﹣x2+bx+c中,y与x的部分对应值如表,则m、n的大小关系为( )
x
……
﹣1
1
3
4
……
y
……
﹣6
m
n
﹣6
……
A.m>n
B.m<n
C.m=n
D.无法确定
【分析】首先确定抛物线的对称轴,然后根据抛物线的对称性求解.
解:∵抛物线经过点(﹣1,﹣6)和(4,﹣6),
∴抛物线的对称轴为=,
∴点(1,m)到对称轴的距离小于点(3,n)到对称轴的距离,
∵a=﹣1<0,
∴抛物线开口向下,
∴m>n,
故选:A.
6.已知反比例函数y=的图象如图所示,则二次函数y=2kx2﹣x+k2的图象大致为( )
A.
B.
C.
D.
【分析】本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.
解:∵函数y=的图象经过二、四象限,∴k<0,
∴抛物线开口向下,对称轴x=﹣=<0,
即对称轴在y轴的左边.
故选:D.
7.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A.
B.
C.
D.
【分析】由图可得∠ACB=135°,AC=,BC=2,然后分别求得A,B,C,D中各三角形的最大角,继而求得答案.
解:如图:∠ACB=135°,AC=,BC=2,
A、最大角=135°,对应两边分别为:1,,
∵:1=2:,
∴此图与△ABC相似;
B、∵最大角<135°,
∴与△ABC不相似;
C、∵最大角<135°,
∴与△ABC不相似;
D、∵最大角<135°,
∴与△ABC不相似.
故选:A.
8.已知直线y=kx(k>0,k是常数)与双曲线y=交于点A(x1,y1),B(x2,y2)两点,则2x1y2﹣x2y1的值为( )
A.5
B.0
C.﹣5
D.﹣10
【分析】由于正比例函数和反比例函数图象都是以原点为中心的中心对称图形,因此它们的交点A、B关于原点成中心对称,则有x2=﹣x1,y2=﹣y1.由A(x1,y1)在双曲线y=上可得x1?y1=5,然后把x2=﹣x1,y2=﹣y1代入2x1y2﹣x2y1的就可解决问题.
解:∵直线y=kx(k>0)与双曲线y=都是以原点为中心的中心对称图形,
∴它们的交点A、B关于原点成中心对称,
∴x2=﹣x1,y2=﹣y1.
∵A(x1,y1)在双曲线y=上,
∴x1?y1=5,
∴2x1y2﹣x2y1=2x1?(﹣y1)﹣(﹣x1)?y1=﹣x1?y1=﹣5.
故选:C.
9.如图,已知经过原点的抛物线y=ax2+bx+c的对称轴是直线x=﹣1,有三个结论,其中正确的个数是( )
①ab>0;
②a+b+c>0;
③当x<﹣2时,y<0.
A.0个
B.1个
C.2个
D.3个
【分析】由抛物线的开口向上,对称轴在y轴左侧,判断a,b与0的关系,得到ab>0,即可判断①;由x=1时,得到y=a+b+c>0,即可判断②;根据对称轴和抛物线与x轴的一个交点,得到另一个交点,然后根据图象即可判断③.
解:①∵抛物线的开口向上,
∴a>0,
∵对称轴在y轴的左侧,
∴b>0
∴ab>0,故①正确;
②∵观察图象知;当x=1时y=a+b+c>0,
故②正确;
③∵抛物线的对称轴为x=﹣1,与x轴交于(0,0),
∴另一个交点为(﹣2,0),
∴当x<﹣2时,y>0,故③错误;
故选:C.
10.为庆祝国庆,某公司要在如图所示的五角星中(图中所有线段的长度均相等,且∠A=∠B=∠C=∠D=∠E=36°),从顶点A开始,沿边每隔25厘米装一盏闪光灯,如果F、J两点间的距离等于(﹣1)米,则需要安装闪光灯的盏数是( )(参考数据:sin18°=)
A.70
B.80
C.79
D.71
【分析】本题需要求出五角星的边长,即求出AF的长.由于五角星是由正五边形各边的延长线相交所得,可得∠A的度数.在等腰△FJ中,根据BC的长和∠ABC的度数,可求出AB的长.即可求出五角星的周长,由此可求出需安装闪光灯的数量.
解:如图:连接FJ,作AM⊥FJ于点M,
∵∠FAJ=∠B=∠C=∠D=∠E=36°,
∴∠FAM=18°,FM=FJ=,
∵sin18°=,
∴=AF,
∴AF=2(米),
∴AF+AJ+JE+EI+ID+DH+HC+CG+BG+BF=2000cm,
则需安装闪光灯:2000÷25=80(盏).
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分。请把你的答案填写在Ⅱ卷对应题号下的横线上。)
11.如图,已知点A在反比例函数y=(k是常数,x<0)的图象上,过点A作AB⊥y轴于B,若△AOB的面积为1,则k的值是 ﹣2 .
【分析】根据△AOB的面积确定k的绝对值为2,再由点A所在象限确定k为﹣2.
解:设点A的坐标为(x,y),且xy=k.
∵点A在第二象限,
∴x<0,y>0.
AB=﹣x,OB=y.
∴S△AOB=AB×OB
=.
∴xy=k=﹣2.
故答案为:﹣2.
12.△ABC中,AB=9cm,AC=40cm,BC=41cm,则△ABC的外接圆半径长是 20.5cm .
【分析】由在△ABC中,AB=9cm,AC=40cm,BC=41cm,可判定△ABC是直角三角形,然后由直角三角形的斜边即是它的外接圆的直径,求得答案.
解:在△ABC中,AB=9cm,AC=40cm,BC=41cm,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,且AB是斜边,
∴△ABC的外接圆半径长为:AB=20.5cm.
故答案为:20.5cm.
13.如图,AB是⊙O的直径,点C在⊙O上,AB=8,∠CAB=20°,D是弧BC的中点,P是直径AB上的一动点,则PC+PD的最小值为 4 .
【分析】作D点关于AB的对称点E,如图,利用对称的性质得到PE=PD,=,再根据两点之间线段最短判断PC+PD的值最小,接着根据圆周角定理得到∠BOC=40°,∠BOE=20°,然后通过证明△COE为等边三角形得到CE的长即可.
解:作D点关于AB的对称点E,连接CE交AB于P,如图,
∵点D与点E关于AB对称,
∴PE=PD,=,
∴PC+PD=PC+PE=CE,
∴此时点P点即为PC+PD的值最小的点,最小值为CE的长度,
∵∠BOC=2∠CAB=2×20°=40°,
而D为弧BC的中点,
∴∠BOE=∠BOC=20°,
∴∠COE=40°+20°=60°,
∴△COE为等边三角形,
∴CE=OC=AB=4,
∴PC+PD的最小值为4.
故答案为:4.
14.对于两个不相等的实数a、b,我们规定符号min{a,b}表示a、b中的较小值,如:min{1,2}=1,按照这个规定,方程min{x,﹣x}=的解为 1﹣ .
【分析】分类讨论x与﹣x的大小,分别求出方程的解,检验即可.
解:当x>﹣x,即x>0时,方程变形得:﹣x=,
整理得:x2+2x+1=0,即(x+1)2=0,
解得:x1=x2=﹣1,不符合题意,舍去;
当x<﹣x,即x<0时,方程变形得:x=,
方程整理得:x2﹣2x=1,即(x﹣1)2=2,
解得:x1=1+(不符合题意,舍去),x2=1﹣,
经检验x=1﹣是分式方程的解,
综上,方程的解为x=1﹣.
三、解答题(本大题共9小题,共90分)解答应写明文字说明和运算步骤.
15.计算:sin245°+cos30°sin30°﹣tan60°.
【分析】直接利用特殊角的三角函数值以及二次根式的性质计算得出答案.
解:原式=×()2+×﹣
=×+﹣
=﹣.
16.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使=,并写出点A2的坐标.
【分析】(1)利用关于x轴对称的点的坐标特征,写出A1、B1、C1的坐标,然后描点即可得到△A
1B1C1;
(2)把A、B、C的横纵坐标后乘以﹣2得到出A2、B2、C2的坐标,然后描点即可得到△A
2B2C2.
解:(1)如图,△A
1B1C1为所作,A1(1,﹣3);
(2)如图,△A2B2C2为所作,A2(﹣2,﹣6).
17.如图,在锐角三角形OAB中,点C,D分别在边OA,OB上,OG⊥AB于点G,OH⊥CD于点H,∠COH=∠GOB.
(1)求证:△ODC∽△OAB;
(2)若OD=3,OA=7,求的值.
【分析】(1)根据垂线的性质得到∠OHC=∠OGB=90°,结合题意∠COH=∠GOB,从而推出△OHC∽OGB,根据相似三角形的性质得到∠OCH=∠B,结合图形中的公共角∠DOC=∠AOB,利用相似三角形的判定定理证明即可;
(2)根据(1)中的结论△ODC∽△OAB,从而利用根据相似三角形的性质进行求解即可.
【解答】(1)证明:∵OG⊥AB于点G,OH⊥CD于点H,
∴∠OHC=∠OGB=90°,
又∠COH=∠GOB,
∴△OHC∽OGB,
∴∠OCH=∠B,
∵∠DOC=∠AOB,
∴△ODC∽△OAB;
(2)由(1)得△ODC∽△OAB,
∴=,
又OD=3,OA=7,
∴=.
18.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
【分析】过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、BP.
解:如图:
过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=20海里,
∴PM=AP=10海里,AM=cos30°AP=10海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10)海里,
∴BP==10海里,
即小船到B码头的距离是10海里,A、B两个码头间的距离是(10+10)海里.
19.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图所示,轨道旁边的测速仪测得弹珠半分钟末的速度为0.5米/分,求:
(1)二次函数和反比例函数的关系式;
(2)弹珠离开轨道时的速度.
【分析】(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=5代入(1)中反比例函数的解析式即可.
解:(1)v=at2的图象经过点(,),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=(2<t≤5);
(2)由图象知,弹珠在第5分钟末离开轨道,速度为=3.2(米/分).
20.某水果店销售某种水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)所示的变化趋势,每千克成本y2(元)与销售时间第x月之间存在如图2(一段抛物线)所示的变化趋势.
(1)分别求函数y1和y2的表达式;
(2)销售这种水果,第几月每千克所获得利润最大?最大利润是多少?
【分析】(1)设y1=kx+b(k≠0),y2=a(x﹣5)2+8,用待定系数法求解即可;
(2)设第x月每千克所获得的利润为w(元),由题意得w关于x的二次函数,根据二次函数的性质可得答案.
解:(1)由题意设y1=kx+b(k≠0),y2=a(x﹣5)2+8,
将(6,10),(9,9)代入y1=kx+b,得:
,
解得,
∴y1=﹣x+12;
将(11,14)代入y2=a(x﹣5)2+8,得:
14=a(11﹣5)2+8,
解得a=,
∴y2=(x﹣5)2+8,
函数y1和y2的表达式分别为y1=﹣x+12,y2=(x﹣5)2+8;
(2)设第x月每千克所获得的利润为w(元),由题意得:
w=﹣x+12﹣[(x﹣5)2+8]
=﹣(x﹣4)2+2.5,
∴当x=4时,w有最大值,w最大=2.5.
∴销售这种水果,第4个月每千克所获得利润最大,最大利润是2.5元.
21.如图,AB是⊙O的直径,C、G是⊙O上两点,且=,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若=,求∠E的度数;
(3)在(2)的条件下,若CD=cm,求⊙O的直径AB的长.
【分析】(1)要证明CD是⊙O的切线,连接OC,只要证明∠OCE=90°即可,根据题目中的条件,可以证明OC∥BD,再根据CD⊥BG于点D,从而可以证明结论成立;
(2)由(1)知,OC∥BD,则△COF∽△BDF,即可得出==,进而得出==,继而得到EO=2OB=2OC,即可得解;
(3)由(2)知∠E=30°,可得∠EBD=60°,∠CBD=30°,继而得出BC=2CD=2cm,BD==3cm,再根据=,即可求出OC,进而求出AB.
【解答】(1)证明:连接OC,
∵OC=OB,=,
∴∠OCB=∠OBC,∠OBC=∠CBD,
∴∠CBD=∠OCB,
∴OC∥BD,
∴∠ECO=∠EDB,
∵CD⊥BG于点D,
∴∠EDB=90°,
∴∠ECO=90°,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)解:由(1)知,OC∥BD,
∴△COF∽△BDF,
∴=,
∵=,
∴=,
∴==,
∴EO=2OB=2OC,
∵∠CEO=90°,
∴∠E=30°;
(3)解:由(2)知,∠E=30°,
∴∠EBD=60°,
∴∠CBD=30°,
∵∠BDE=90°,CD=cm,
∴BC=2CD=2cm,
∴BD==3cm,
由(2)知,=,
∴OC=2cm,
∴AB=4(cm),
答:⊙O的直径AB的长是4cm.
22.如图,在△ABC中,∠ACB=90°,BC=2,AC=4,点D在边BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式.
【分析】(1)由ED=EB得到∠B=∠DEB,再根据等角的余角相等得到∠A=∠FEG,加上公共角∠G,则可判断△EFG∽△AEG;
(2)过E点作EH⊥AC于H,如图,先证明△AEF∽△ACB得到==,再利用△EFG∽△AEG得到===,则EG=2x,GA=4x,AF=3x,在Rt△AEF中利用勾股定理可求出EF=x,AE=x,接着利用面积法求出EH=x,然后根据三角形面积公式得到y关于x的函数解析式.
【解答】(1)证明:∵ED=EB,
∴∠B=∠DEB,
∵∠ACB=90°,
∴∠A+∠B=90°,
∵EF⊥AB,
∴∠FBE=90°,
∴∠DEB+∠FEG=90°,
∴∠A=∠FEG,
∵∠EGF=∠AGE,
∴△EFG∽△AEG;
(2)解:过E点作EH⊥AC于H,如图,
∵∠AEF=∠ACB,∠EAF=∠CAB,
∴△AEF∽△ACB,
∴=,
∴===,
∵△EFG∽△AEG,
∴===,
∵FG=x,
∴EG=2x,GA=4x,
∴AF=3x,
在Rt△AEF中,∵EF2+AE2=AF2,
∴EF2+4EF2=(3x)2,解得EF=x,
∴AE=x,
∵EH?AF=EF?AE,
∴EH==x,
∴△EFG的面积=?FG?EH=?x?x=x2,
即y关于x的函数解析式为y=x2.
23.如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,﹣),且与x轴交于A、B两点(点A在点B的右侧),与y轴交于C点,点C的坐标为(0,﹣4),P是抛物线上的一个动点,且横坐标为m.
(1)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求点P的横坐标m的取值范围;
(3)当m<0时,过点P作y轴的垂线PQ,垂足为Q.问:是否存在点P,使∠QPO=∠BCO?若存在,请求出点P的坐标;若不存在,请说明理由.
【分析】(1)根据顶点D的坐标为(1,﹣),可设抛物线表达式为:y=a(x﹣1)2﹣,将C(0,﹣4)代入,即可得抛物线表达式为:y=x2﹣x﹣4;
(2)若∠PAO=45°,过P作PG⊥x轴于G,①可证明△AOC是等腰直角三角形,故∠CAO=45°,若动点P满足∠PAO不大于45°,则m≤0,②△PAG是等腰直角三角形,可得m2﹣m﹣4=4﹣m,解得m=4(舍去)或m=﹣4,若动点P满足∠PAO不大于45°,则m≥﹣4;故可得答案:﹣4≤m≤0;
(3)①当P在第二象限,由∠QPO=∠BCO,∠PQO=∠BOC,得△PQO∽△COB,故=,即=,可得P(,);
②当P在第三象限,同理可得P(,).
解:(1)根据题意设抛物线表达式为:y=a(x﹣1)2﹣,
将C(0,﹣4)代入得:a﹣=﹣4,
∴a=,
∴抛物线表达式为:y=(x﹣1)2﹣=x2﹣x﹣4;
(2)若∠PAO=45°,过P作PG⊥x轴于G,如图:
①在y=x2﹣x﹣4中,令y=0,得x2﹣x﹣4=0,
解得x=﹣2或x=4,
∴A(4,0),B(﹣2,0),
在y=x2﹣x﹣4中,令x=0,得y=4,
∴C(0,4),
∴OA=OC,
∴△AOC是等腰直角三角形,
∴∠CAO=45°,
若动点P满足∠PAO不大于45°,则m≤0,
②∵∠PAO=45°,
∴△PAG是等腰直角三角形,
∴PG=AG,
而P(m,m2﹣m﹣4),
∴m2﹣m﹣4=4﹣m,
解得m=4(舍去)或m=﹣4,
∴若动点P满足∠PAO不大于45°,则m≥﹣4;
由①②可得:﹣4≤m≤0;
(3)存在,理由如下:
①当P在第二象限,如图:
∵∠QPO=∠BCO,∠PQO=∠BOC,
∴△PQO∽△COB,
∴=,
∵B(﹣2,0),C(0,4),P(m,m2﹣m﹣4),
∴=,
解得m=(舍去)或m=,
∴P(,);
②当P在第三象限,如图:
同①可得△POQ∽△CBO,
∴=,即=,
解得m=(舍去)或m=,
∴P(,),
综上所述,当∠QPO=∠BCO时,P的坐标为:(,)或(,).
同课章节目录
