七年级数学多边形及其内角和
图片预览








文档简介
(共55张PPT)
温故而知新
在△ABC中,
(1)∠C = 90 ,∠B=30 , 则 ∠A = ;
(2)∠A = 100 ,∠B=∠C , 则 ∠B = ;
(3)若△ABC中的三个内角度数之比为2:3:4,
则相应外角之比为 .
(4)三角形的三个内角中,最多有 个锐角,最
多有 个直角,最多有 个钝角.
§7.3.1多边形
观察下列图案
由这图形你抽象出什么几何图形?
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
长方形
生活中的平面图形
由这图形你抽象出什么几何图形?
由这图形你抽象出什么几何图形?
四边形
生活中的平面图形
六边形
生活中的平面图形
由这图形你抽象出什么几何图形?
八边形
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
长方形
六边形
四边形
八边形
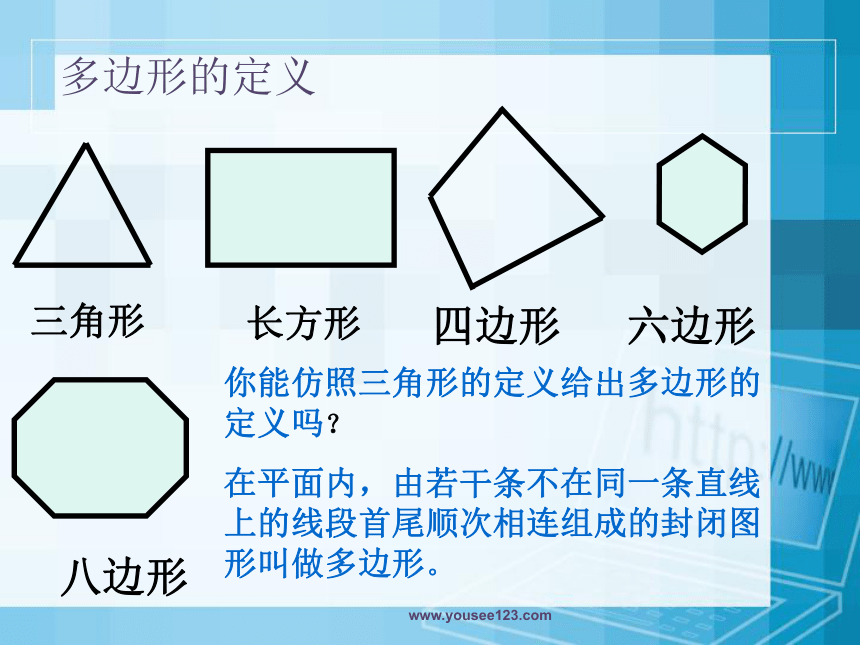
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
多边形的定义
你能仿照三角形的定义给出多边形的定义吗?
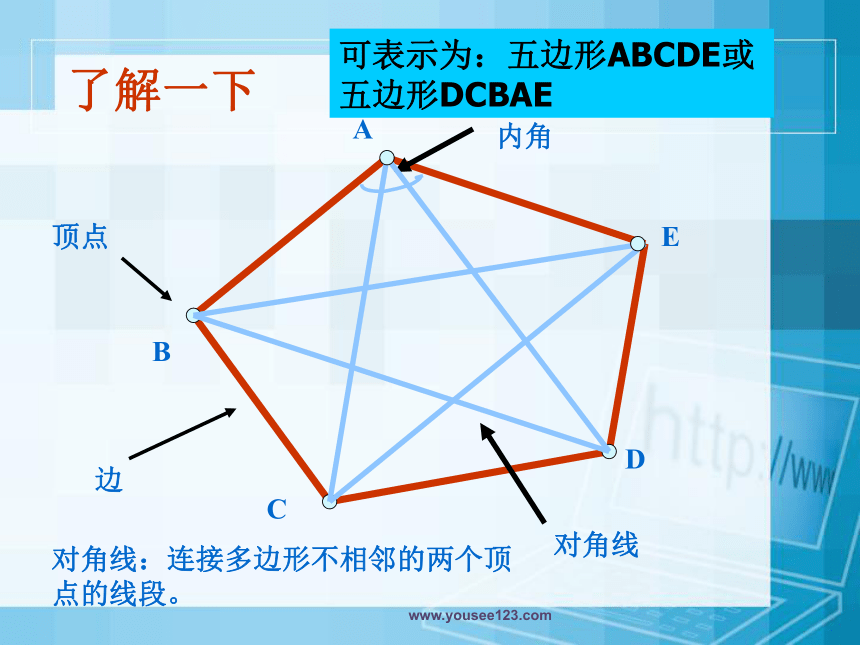
了解一下
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
A
B
C
D
1
2
3
4
5
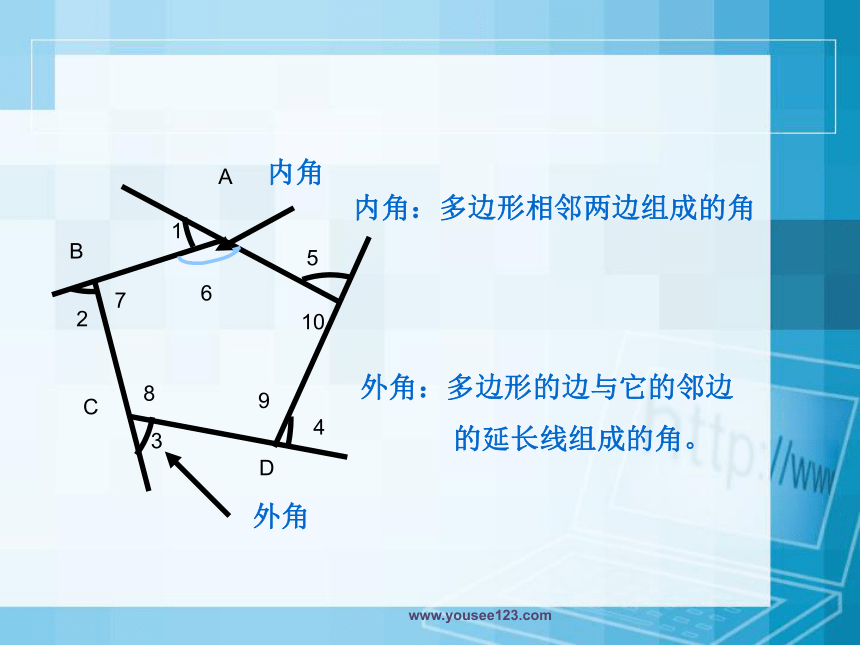
内角:多边形相邻两边组成的角
外角:多边形的边与它的邻边
的延长线组成的角。
内角
外角
6
7
8
9
10
比一比
你能说出这两幅图形的异同点吗?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个四边形都在这条直线的同一侧,那么这个多边形就是凸多边形。本节我们只讨论凸多边形。
想一想:
观察下面多边形,它们的边,角有什么特点?
在平面内,内角都相等,边也都相等的多边形叫做正多边形
7.3.2 多边形的内角和
1、在平面内,_____________________叫做多边形。
2、在多边形中连接_________________的线段叫做多边形的对角线。
3、三角形的内角和是_____度.
4、你能够利用三角形的内角和求四边形的内角和吗?试试看?
A
B
C
D
思路:多边形问题转化为三角形问题来解决.
四边形的内角和为3600
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点的线段
1800
问题,新知
长方形的内角和是多少?为什么?
如果是任意四边形呢?
B
A
D
C
(1)四边形ABCD的内角 和是多少?
(2)你是怎样求的?
(1)从顶点A可以画几条对角线?分别是哪几条?
(2)这样五边形被分成了几个三角形?
(3)五边形的内角和是多少度?
A
B
D
C
E
你来探索六边形的内角和,你一定行!
A
B
C
D
E
F
被分得三角形个数
六边形的内角和
4
4×180°
这种探索方法你掌握了吗?请完成下表
多边形的边数 3 4 5 6 7 … n
分成的三角形个数 1 2 …
多边形的内角和 180° 180° ×2 180° ×3 …
3
4
5
n-2
180°
×5
(n-2) ×180
180° ×4
想一想:从表中你能发现什么?
n边形的内角和等于(n-2).180°
想一想
An A5
A1 A4
A2 A3
An A5
A1 A4
A2 A3
P
P
(1)
(2)
你还有其他的方法将多边形分割成三角形吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 °
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
例2:一个正多边形的一个内角为150°,
你知道它是几边形吗?
解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。
另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正 多边形的边数等于
360°÷30°=12。
例题、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+( y -2)·180=1440
x : y=1 : 3
解之得 x =3
y =9
答:它们的边数分别是3和9。
牛刀小试:
(1)八边形的内角和等于 。
(2)已知一个多边形的内角和等于2340°,
它的边数是 。
(3)小明在计算多边形的内角和时求得的
度数是1000°,他的答案正确吗?为
什么?
1080°
15
(4)已知四边形4个内角的度数比是1︰2︰3︰4,
那么这个四边形中最大角的度数是 。
(5)一个五边形的三个内角是直角,另两个内角
都是n°,则n= 。
(6)六角螺母的面是六边形,它的内角都相等,则
这个六边形的每个内角是 。
(7)在四边形ABCD中,∠A与∠C互补,那么∠B
与∠D有什么关系呢?为什么?
144°
135°
120°
问题
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
探索
(1)什么是三角形的外角?外角有什么性质?
(2)类似地,在多边形中找出外角
多边形的一边与另一边的延长线的夹角,叫做多边形的外角。
做一做
(1)如图,求△ABC的三个外角的和。
三角形的三个外角之和为3600
(2)四边形的外角和等于多少度?
(3)五边形的外角和怎么求?n边形呢?
猜想与说理:
n边形的外角和是多少度呢
答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
例3:一个多边形的内角和等
于它的外角和的3倍,它
是几边形?
解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
例3:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
(1)一个多边形的每一个外角都是600,这个多边形是几边形?它的内角和等于多少度
(2)有没有这样的多边形,它的内角和是外角和的3倍?
(3)一个多边形的每一个外角都相等,且每一个内角都比外角大900,求这个多边形的边数和每个内角的度数。
7、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
6、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
5、四边形的四个内角的比是8:6:3:7,求它的四个内角,
4、一个多边形的内角和是外角和的4倍,这是几边形
三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
C
C
3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
A
D
5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;
360
(1)、(2)、(4)
7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。
65°
60°
A
B
C
D
1
2
E
8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
把一个五边形切取一个角,将得到几边形?此时多边形的内角与外角有什么变化?
探究活动:
A
B
C
D
如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。
E
E
100 °
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
G
180 °
G
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
1
2
3
4
5
180 °
巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
(4)求∠A+∠B+∠C+∠D+∠E+∠F的度数。
温故而知新
在△ABC中,
(1)∠C = 90 ,∠B=30 , 则 ∠A = ;
(2)∠A = 100 ,∠B=∠C , 则 ∠B = ;
(3)若△ABC中的三个内角度数之比为2:3:4,
则相应外角之比为 .
(4)三角形的三个内角中,最多有 个锐角,最
多有 个直角,最多有 个钝角.
§7.3.1多边形
观察下列图案
由这图形你抽象出什么几何图形?
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
长方形
生活中的平面图形
由这图形你抽象出什么几何图形?
由这图形你抽象出什么几何图形?
四边形
生活中的平面图形
六边形
生活中的平面图形
由这图形你抽象出什么几何图形?
八边形
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
长方形
六边形
四边形
八边形
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
多边形的定义
你能仿照三角形的定义给出多边形的定义吗?
了解一下
顶点
内角
边
对角线
对角线:连接多边形不相邻的两个顶点的线段。
可表示为:五边形ABCDE或五边形DCBAE
A
B
C
D
E
A
B
C
D
1
2
3
4
5
内角:多边形相邻两边组成的角
外角:多边形的边与它的邻边
的延长线组成的角。
内角
外角
6
7
8
9
10
比一比
你能说出这两幅图形的异同点吗?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个四边形都在这条直线的同一侧,那么这个多边形就是凸多边形。本节我们只讨论凸多边形。
想一想:
观察下面多边形,它们的边,角有什么特点?
在平面内,内角都相等,边也都相等的多边形叫做正多边形
7.3.2 多边形的内角和
1、在平面内,_____________________叫做多边形。
2、在多边形中连接_________________的线段叫做多边形的对角线。
3、三角形的内角和是_____度.
4、你能够利用三角形的内角和求四边形的内角和吗?试试看?
A
B
C
D
思路:多边形问题转化为三角形问题来解决.
四边形的内角和为3600
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点的线段
1800
问题,新知
长方形的内角和是多少?为什么?
如果是任意四边形呢?
B
A
D
C
(1)四边形ABCD的内角 和是多少?
(2)你是怎样求的?
(1)从顶点A可以画几条对角线?分别是哪几条?
(2)这样五边形被分成了几个三角形?
(3)五边形的内角和是多少度?
A
B
D
C
E
你来探索六边形的内角和,你一定行!
A
B
C
D
E
F
被分得三角形个数
六边形的内角和
4
4×180°
这种探索方法你掌握了吗?请完成下表
多边形的边数 3 4 5 6 7 … n
分成的三角形个数 1 2 …
多边形的内角和 180° 180° ×2 180° ×3 …
3
4
5
n-2
180°
×5
(n-2) ×180
180° ×4
想一想:从表中你能发现什么?
n边形的内角和等于(n-2).180°
想一想
An A5
A1 A4
A2 A3
An A5
A1 A4
A2 A3
P
P
(1)
(2)
你还有其他的方法将多边形分割成三角形吗?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
多了什么?如何处理?
多了什么?如何处理?
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °= (n-2)×180 °
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
例2:一个正多边形的一个内角为150°,
你知道它是几边形吗?
解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。
另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正 多边形的边数等于
360°÷30°=12。
例题、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+( y -2)·180=1440
x : y=1 : 3
解之得 x =3
y =9
答:它们的边数分别是3和9。
牛刀小试:
(1)八边形的内角和等于 。
(2)已知一个多边形的内角和等于2340°,
它的边数是 。
(3)小明在计算多边形的内角和时求得的
度数是1000°,他的答案正确吗?为
什么?
1080°
15
(4)已知四边形4个内角的度数比是1︰2︰3︰4,
那么这个四边形中最大角的度数是 。
(5)一个五边形的三个内角是直角,另两个内角
都是n°,则n= 。
(6)六角螺母的面是六边形,它的内角都相等,则
这个六边形的每个内角是 。
(7)在四边形ABCD中,∠A与∠C互补,那么∠B
与∠D有什么关系呢?为什么?
144°
135°
120°
问题
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
A
B
C
D
E
1
2
3
4
5
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
探索
(1)什么是三角形的外角?外角有什么性质?
(2)类似地,在多边形中找出外角
多边形的一边与另一边的延长线的夹角,叫做多边形的外角。
做一做
(1)如图,求△ABC的三个外角的和。
三角形的三个外角之和为3600
(2)四边形的外角和等于多少度?
(3)五边形的外角和怎么求?n边形呢?
猜想与说理:
n边形的外角和是多少度呢
答:都是360°.因为多边形的外角与它相邻的内角是邻补角,所以n边形的外角和加内角和等于n·180°,内角和为(n-2)·180°,因此,外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
例3:一个多边形的内角和等
于它的外角和的3倍,它
是几边形?
解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
例3:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
(1)一个多边形的每一个外角都是600,这个多边形是几边形?它的内角和等于多少度
(2)有没有这样的多边形,它的内角和是外角和的3倍?
(3)一个多边形的每一个外角都相等,且每一个内角都比外角大900,求这个多边形的边数和每个内角的度数。
7、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
6、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,
5、四边形的四个内角的比是8:6:3:7,求它的四个内角,
4、一个多边形的内角和是外角和的4倍,这是几边形
三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
C
C
3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
A
D
5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;
360
(1)、(2)、(4)
7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。
65°
60°
A
B
C
D
1
2
E
8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,
2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
把一个五边形切取一个角,将得到几边形?此时多边形的内角与外角有什么变化?
探究活动:
A
B
C
D
如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。
E
E
100 °
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
G
180 °
G
探究活动:
A
B
C
D
如图, ∠A+∠B+∠C+∠E+∠F= 。
E
F
1
2
3
4
5
180 °
巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。
A
G
F
E
D
C
B
7×180O-2×360O=540O
(4)求∠A+∠B+∠C+∠D+∠E+∠F的度数。
