七年级数学轴对称图形复习
图片预览









文档简介
(共45张PPT)
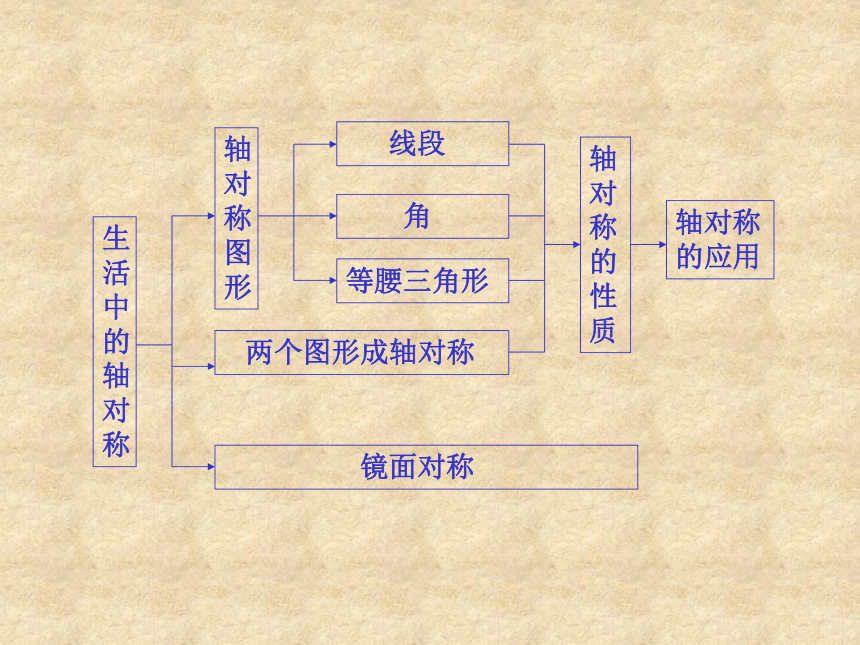
第一章生活中的轴对称
复习
20世纪著名数学家赫尔曼·外 尔所说的,“对称是一种思想,人们毕生追求,并创造次序、美丽和完善……”
生活中的轴对称
轴对称的性质
轴对称图形
两个图形成轴对称
镜面对称
线段
角
等腰三角形
轴对称的应用
本章知识回顾
轴对称图形:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,则称这个图形是轴对称图形。
成轴对称:如果两个图形沿一条直线对折后,它们能完全重合,则称这两个图形成轴对称
对称轴:这一条直线叫对称轴
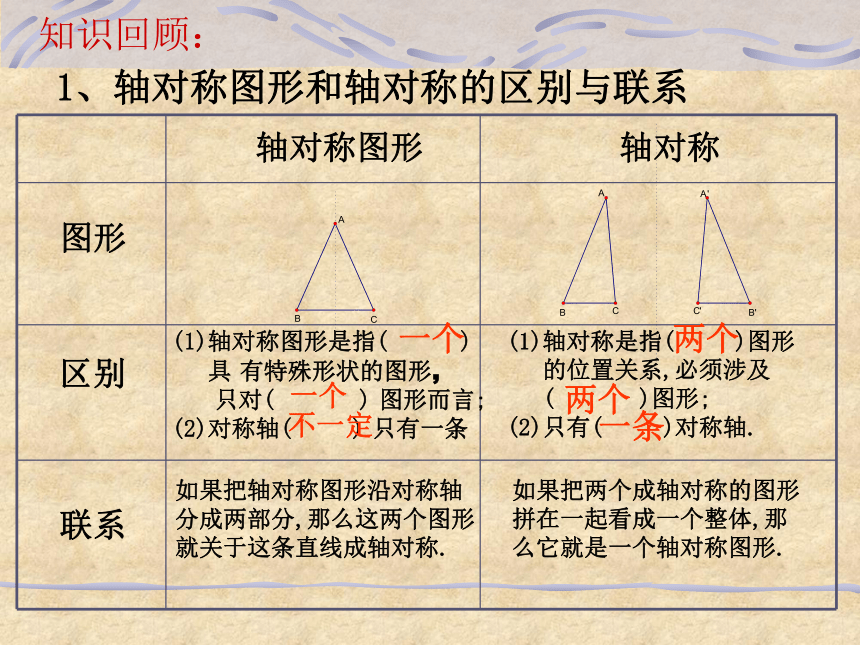
1、轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
(1)轴对称图形是指( )
具 有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.
如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
知识回顾:
角平分线性质
角平分线所在的直线是角的对称轴
角平分线上的点到这个角的两边距离相等
线段垂直平分线性质
线段的垂直平分线是线段的一条对称轴
线段垂直平分线上的点到这条线段的两端距离相等
等腰三角形
等腰三角形是轴对称图形
它的对称轴是底边上的中线、底边上的高、顶角的角平分线所在的直线。并且三线合一。
等边对等角、等角对等边
等边三角形是特殊的等腰三角形。
轴对称的性质
对应点所连的线段被对称轴垂直平分
对应线段相等,对应角相等
我们一起来做个游戏。游戏规则:将走道抽象成一条直线,将每位同学抽象成一个点,现在以这条直线为对称轴,老师报一个同学的学号也就是确定一个点(报到学号的同学立刻起立),请表示其对称点的这位同学也立刻起立,并回答:“我叫某某某,我是某某某的对称点。”
放松一下:
1、国旗是一个国家的象征,观察下面的国旗,是轴对称图形的是( )
A.加拿大、韩国、乌拉圭 B.加拿大、瑞典、澳大利亚
C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士
加拿大 韩国 澳大利亚 乌拉圭 瑞典 瑞士
C
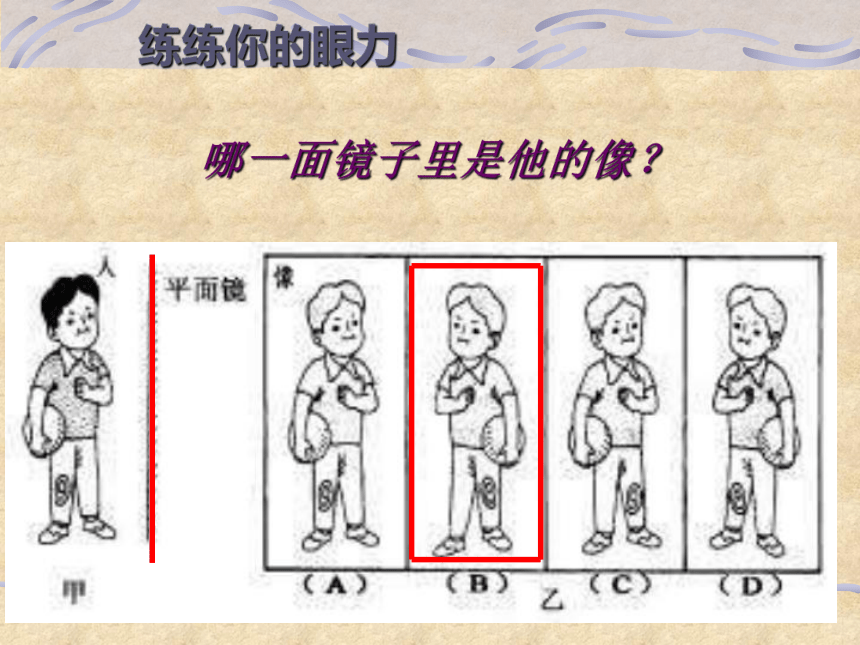
哪一面镜子里是他的像?
练练你的眼力
3、△ABC与△DEF关于直线L成轴对称,则∠C是多少度?
L
1、 一个角的角平分线就是这个角的对称轴.( )
判断
×
2、 直线BD是长方形ABCD的对称轴.( )
×
4 、如图,在△ABC中,∠ABC的角平分线交AC于P,一个同学马上就得到PA=PC,你觉得对吗
CP
=
1.90
厘米
AP
=
2.10
厘米
P
C
B
A
E
F
当BA=BC时,有PA=PC
2、轴对称图形的对应线段相等,对应角相等。
3、如果一个图形是轴对称图形,那么连结对称点的线段与对称轴关系 。
对称轴垂直平分连结对称点的线段
4、线段的垂直平分线的点到 的 距离相等。
这条线段两端点
5、一个角的角平分线上的点到 的距离相等。
这个角的两边
3、“有一个等腰三角形的两条边长分别是4cm和8cm,则当腰长为4cm时,这个等腰三角形的周长为16cm;当腰长为8cm时,这个等腰三角形的周长为20cm。”这个说法正确吗?为什么?
耐心做一做:
1、等腰三角形的对称轴最多有 条,最少有 条,圆的对称轴有 条,它的对称轴是 。
2、以下是部分常用的交通标志图,仔细观察哪些是轴对称图形?
(1) (2) (3) (4) (5) (6)
3、如图,画出所示图形关于直线l的对称图形。
A
l
l
A
B
C
l
l
(1) (2)
3
1
B
答:轴对称图形是: (1)(2)(3)(5)(6)。
无数
直径所在的直线
4、如图,是齐新新同学照镜子时看到的
对面墙上钟表指针的情况,你能告诉
他当时的时间大约是几点几分吗? 、
5、如图:在△ABC中,DE是AC的垂直平分线,AC=5厘米,△ABD的周长等于13厘米,则△ABC的周长是 。
A
B
D
E
C
6、如图:在△ABC中,∠ C=900,AD平分∠ BAC,DE⊥AB交AB于E,BC=30,BD:CD=3:2,则DE= 。
A
B
C
D
18厘米
E
12
7、研究下列数字,找出它们的规律,并加以猜想:
121=112,12321=1112,…..,123…9…321=( )2
111111111
答:当时的时间大约是四点十分。
1、如图, (1)等腰△ABC中,AB=AC,
顶角∠A=100°,那么底角
∠B= , ∠C= 。
B
A
C
(2)△ABC中,AB=AC,
∠B=72°,那么∠A= 。
(3)等腰△ABC中有一个角为50°,那么另外两个角分别是多少?
36°
40°
40°
2、如图,在△ABC中,AB=AC时,
(1)∵AD⊥BC
∴∠ ____= ∠_____;____=____
(2) ∵AD是中线
∴____⊥____; ∠_____= ∠_____
(3) ∵ AD是角平分线
∵____ ⊥____;_____=____
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
答:相等。
∵ AO平分∠BAC
∴ ∠EAO= ∠DAO
∵ OE⊥AB,OD⊥AC
∴ ∠AEO= ∠ADO
∴由
∠AEO= ∠ADO
∠EAO= ∠DAO
AO=AO
得⊿ AEO≌⊿ ADO(AAS)
∴OE=OD
试
一
试
下面用我们学过的知识证明发现:
如图,已知AO平分∠BAC,OE⊥AC,OD⊥AB 。则OE=OD吗?请说明理由。
A
B
C
E
D
O
如图,已知AD是BC的中垂线,所能得到的结论是:
你能根据现有条件,推得∠ABD=∠ACD
如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
MN是AB的垂直平分线,EF是BC垂直平分线。PA与PC是否相等,为什么?
M
E
P
A
B
C
F
N
如图,P、Q是△ABC边上的两点,BP=PQ=QC=AP=AQ,
求∠BAC的度数。
P
A
B
C
Q
1、① 如图, AB//CD,∠ACD的角平分线交AB与E,想一想△ACE是什么三角形.
② 如图, ∠ABC、∠ACB的平分线相 交于F,过F作DE//BC交AB于D,交AC于E,若AB=9cm, AC=8cm,则△ADE的周长是多少
F
E
D
C
B
A
AC=AE+EC=AE+EF
AB=AD+DB=AD+DF
某开发区新建了两片住宅区:A区、B区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短
A小区
B 小区
煤气主管道
)
)
)
A
如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN,请你用折纸的方法找出P点并说明理由。
B
C
M
N
·
·
如图,古罗马有一位将军,他每天都要从驻地A 出发,到河边饮马,再到河岸同侧的军营B 巡视。他经常想因该怎样走才能使路程最短,但他百思不得其解。
2、某居民小区搞绿化,要在一块长方形空地上建花坛,现征集设计方案,要设计的图案由圆和正方形组成( 圆与正方形的个数不限),并且使整个长方形场地成轴对称 ,请在下边长方形中画出你的设计方案.
例3 几年前,老李承包了一个正方形的鱼塘,当时为了更好地管理鱼塘和住宿方便,老李在鱼塘四个角落处各盖了一间小屋(如图),现在他决定将现有鱼塘扩大1倍,而四角的小屋不拆,请你帮他设计一种方案,满足他的要求?
拓展题:动手折一折
将图中的三角形纸片沿虚线折叠,图中由粗实线围成的图形面积与三角形面积之比为2:3,已知图中三个阴影的三角形面积之和为1,试确定重叠部分的面积。
解:设重叠部分的面积为x, 则粗实线围成的图形面积为1+ x ,三角形面积为1+ 2 x 。
由题意得,1+x=2\3(1+2x)
解得 x=1
答:重叠部分的面积为1。
例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动, A1 与A2 间的距离改变吗?
A
L1
L2
A1
A2
B
C
解:如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动, A1与A2 间的距离改变吗?
A
L1
L2
A1
A2
B
C
解: (1)如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
(2)答:不论A 在L1,L2间的哪个位置,A1与A2 间的距离都不会改变吗。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
(1)当汽车行驶到什么位置时距村庄M最近?行驶到什么位置时距村庄N最近?
答:如图 ,当汽车行驶到P1时,距村庄M最近,
当汽车行驶到P2时,距村庄N最近。
A
B
M
N
P1
P2
根据:直线外一点与直线上各点连结的所有线段中,
垂线段最短。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
(2)当汽车行驶到什么位置时,与村庄M、N的距离相等?
答:如图 ,当汽车行驶到P3时,与村庄M、N的距离相等。
A
B
M
N
P3
根据:线段的垂直平分线上的点到这条线段两个端点的距离相等。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
(3)当汽车行驶到什么位置时,到村庄M、N的距离之和最短?
答:如图 ,当汽车行驶到P4时,到村庄M、N的距离之和最短。
A
B
M
N
P4
根据:两点之间线段最短。
又问:若村庄M,N在公路AB的同侧,则又如何解决此题?
N1
P5
M
N
A
B
答:若村庄M,N在公路AB的同侧时,当汽车行驶到P5时,到村庄M、N的距离之和最短。
,
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
答:如图 ,当汽车行驶到P 时,到村庄M、N的距离之差最大。
(4)是否存在一点P,使汽车行驶到该点时,汽车到村庄M、N的距离之差最大?如果存在,请指出该点的位置;如果不存在,请说明理由。
B
M
N
A
N1
P
1.再次感受对称美,再次认识轴对称及其性质;
2.运用轴对称的性质解决一些实际问题。
第一章生活中的轴对称
复习
20世纪著名数学家赫尔曼·外 尔所说的,“对称是一种思想,人们毕生追求,并创造次序、美丽和完善……”
生活中的轴对称
轴对称的性质
轴对称图形
两个图形成轴对称
镜面对称
线段
角
等腰三角形
轴对称的应用
本章知识回顾
轴对称图形:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,则称这个图形是轴对称图形。
成轴对称:如果两个图形沿一条直线对折后,它们能完全重合,则称这两个图形成轴对称
对称轴:这一条直线叫对称轴
1、轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
(1)轴对称图形是指( )
具 有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.
如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.
如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
知识回顾:
角平分线性质
角平分线所在的直线是角的对称轴
角平分线上的点到这个角的两边距离相等
线段垂直平分线性质
线段的垂直平分线是线段的一条对称轴
线段垂直平分线上的点到这条线段的两端距离相等
等腰三角形
等腰三角形是轴对称图形
它的对称轴是底边上的中线、底边上的高、顶角的角平分线所在的直线。并且三线合一。
等边对等角、等角对等边
等边三角形是特殊的等腰三角形。
轴对称的性质
对应点所连的线段被对称轴垂直平分
对应线段相等,对应角相等
我们一起来做个游戏。游戏规则:将走道抽象成一条直线,将每位同学抽象成一个点,现在以这条直线为对称轴,老师报一个同学的学号也就是确定一个点(报到学号的同学立刻起立),请表示其对称点的这位同学也立刻起立,并回答:“我叫某某某,我是某某某的对称点。”
放松一下:
1、国旗是一个国家的象征,观察下面的国旗,是轴对称图形的是( )
A.加拿大、韩国、乌拉圭 B.加拿大、瑞典、澳大利亚
C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士
加拿大 韩国 澳大利亚 乌拉圭 瑞典 瑞士
C
哪一面镜子里是他的像?
练练你的眼力
3、△ABC与△DEF关于直线L成轴对称,则∠C是多少度?
L
1、 一个角的角平分线就是这个角的对称轴.( )
判断
×
2、 直线BD是长方形ABCD的对称轴.( )
×
4 、如图,在△ABC中,∠ABC的角平分线交AC于P,一个同学马上就得到PA=PC,你觉得对吗
CP
=
1.90
厘米
AP
=
2.10
厘米
P
C
B
A
E
F
当BA=BC时,有PA=PC
2、轴对称图形的对应线段相等,对应角相等。
3、如果一个图形是轴对称图形,那么连结对称点的线段与对称轴关系 。
对称轴垂直平分连结对称点的线段
4、线段的垂直平分线的点到 的 距离相等。
这条线段两端点
5、一个角的角平分线上的点到 的距离相等。
这个角的两边
3、“有一个等腰三角形的两条边长分别是4cm和8cm,则当腰长为4cm时,这个等腰三角形的周长为16cm;当腰长为8cm时,这个等腰三角形的周长为20cm。”这个说法正确吗?为什么?
耐心做一做:
1、等腰三角形的对称轴最多有 条,最少有 条,圆的对称轴有 条,它的对称轴是 。
2、以下是部分常用的交通标志图,仔细观察哪些是轴对称图形?
(1) (2) (3) (4) (5) (6)
3、如图,画出所示图形关于直线l的对称图形。
A
l
l
A
B
C
l
l
(1) (2)
3
1
B
答:轴对称图形是: (1)(2)(3)(5)(6)。
无数
直径所在的直线
4、如图,是齐新新同学照镜子时看到的
对面墙上钟表指针的情况,你能告诉
他当时的时间大约是几点几分吗? 、
5、如图:在△ABC中,DE是AC的垂直平分线,AC=5厘米,△ABD的周长等于13厘米,则△ABC的周长是 。
A
B
D
E
C
6、如图:在△ABC中,∠ C=900,AD平分∠ BAC,DE⊥AB交AB于E,BC=30,BD:CD=3:2,则DE= 。
A
B
C
D
18厘米
E
12
7、研究下列数字,找出它们的规律,并加以猜想:
121=112,12321=1112,…..,123…9…321=( )2
111111111
答:当时的时间大约是四点十分。
1、如图, (1)等腰△ABC中,AB=AC,
顶角∠A=100°,那么底角
∠B= , ∠C= 。
B
A
C
(2)△ABC中,AB=AC,
∠B=72°,那么∠A= 。
(3)等腰△ABC中有一个角为50°,那么另外两个角分别是多少?
36°
40°
40°
2、如图,在△ABC中,AB=AC时,
(1)∵AD⊥BC
∴∠ ____= ∠_____;____=____
(2) ∵AD是中线
∴____⊥____; ∠_____= ∠_____
(3) ∵ AD是角平分线
∵____ ⊥____;_____=____
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
答:相等。
∵ AO平分∠BAC
∴ ∠EAO= ∠DAO
∵ OE⊥AB,OD⊥AC
∴ ∠AEO= ∠ADO
∴由
∠AEO= ∠ADO
∠EAO= ∠DAO
AO=AO
得⊿ AEO≌⊿ ADO(AAS)
∴OE=OD
试
一
试
下面用我们学过的知识证明发现:
如图,已知AO平分∠BAC,OE⊥AC,OD⊥AB 。则OE=OD吗?请说明理由。
A
B
C
E
D
O
如图,已知AD是BC的中垂线,所能得到的结论是:
你能根据现有条件,推得∠ABD=∠ACD
如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
MN是AB的垂直平分线,EF是BC垂直平分线。PA与PC是否相等,为什么?
M
E
P
A
B
C
F
N
如图,P、Q是△ABC边上的两点,BP=PQ=QC=AP=AQ,
求∠BAC的度数。
P
A
B
C
Q
1、① 如图, AB//CD,∠ACD的角平分线交AB与E,想一想△ACE是什么三角形.
② 如图, ∠ABC、∠ACB的平分线相 交于F,过F作DE//BC交AB于D,交AC于E,若AB=9cm, AC=8cm,则△ADE的周长是多少
F
E
D
C
B
A
AC=AE+EC=AE+EF
AB=AD+DB=AD+DF
某开发区新建了两片住宅区:A区、B区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短
A小区
B 小区
煤气主管道
)
)
)
A
如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN,请你用折纸的方法找出P点并说明理由。
B
C
M
N
·
·
如图,古罗马有一位将军,他每天都要从驻地A 出发,到河边饮马,再到河岸同侧的军营B 巡视。他经常想因该怎样走才能使路程最短,但他百思不得其解。
2、某居民小区搞绿化,要在一块长方形空地上建花坛,现征集设计方案,要设计的图案由圆和正方形组成( 圆与正方形的个数不限),并且使整个长方形场地成轴对称 ,请在下边长方形中画出你的设计方案.
例3 几年前,老李承包了一个正方形的鱼塘,当时为了更好地管理鱼塘和住宿方便,老李在鱼塘四个角落处各盖了一间小屋(如图),现在他决定将现有鱼塘扩大1倍,而四角的小屋不拆,请你帮他设计一种方案,满足他的要求?
拓展题:动手折一折
将图中的三角形纸片沿虚线折叠,图中由粗实线围成的图形面积与三角形面积之比为2:3,已知图中三个阴影的三角形面积之和为1,试确定重叠部分的面积。
解:设重叠部分的面积为x, 则粗实线围成的图形面积为1+ x ,三角形面积为1+ 2 x 。
由题意得,1+x=2\3(1+2x)
解得 x=1
答:重叠部分的面积为1。
例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动, A1 与A2 间的距离改变吗?
A
L1
L2
A1
A2
B
C
解:如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
例1 如图:设L1,L2是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A1,A在镜L2中的像为A2,当L1,L2间的距离为18厘米。
(1)试求A1与A2间的距离;
(2)若小球在L1,L2间运动, A1与A2 间的距离改变吗?
A
L1
L2
A1
A2
B
C
解: (1)如图,∵ A 与 A1关于L1对称, A 与 A2关于L2对称
∴ A1 B=AB, A2 C=AC
∴A1A2=2BC=36厘米
答:A1与A2间的距离为36厘米。
(2)答:不论A 在L1,L2间的哪个位置,A1与A2 间的距离都不会改变吗。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
(1)当汽车行驶到什么位置时距村庄M最近?行驶到什么位置时距村庄N最近?
答:如图 ,当汽车行驶到P1时,距村庄M最近,
当汽车行驶到P2时,距村庄N最近。
A
B
M
N
P1
P2
根据:直线外一点与直线上各点连结的所有线段中,
垂线段最短。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
(2)当汽车行驶到什么位置时,与村庄M、N的距离相等?
答:如图 ,当汽车行驶到P3时,与村庄M、N的距离相等。
A
B
M
N
P3
根据:线段的垂直平分线上的点到这条线段两个端点的距离相等。
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
(3)当汽车行驶到什么位置时,到村庄M、N的距离之和最短?
答:如图 ,当汽车行驶到P4时,到村庄M、N的距离之和最短。
A
B
M
N
P4
根据:两点之间线段最短。
又问:若村庄M,N在公路AB的同侧,则又如何解决此题?
N1
P5
M
N
A
B
答:若村庄M,N在公路AB的同侧时,当汽车行驶到P5时,到村庄M、N的距离之和最短。
,
例2 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,
答:如图 ,当汽车行驶到P 时,到村庄M、N的距离之差最大。
(4)是否存在一点P,使汽车行驶到该点时,汽车到村庄M、N的距离之差最大?如果存在,请指出该点的位置;如果不存在,请说明理由。
B
M
N
A
N1
P
1.再次感受对称美,再次认识轴对称及其性质;
2.运用轴对称的性质解决一些实际问题。
