贵州省黔西南州同源高中2020-2021学年高二下学期期末考试数学(理)试题 (Word版含答案解析)
文档属性
| 名称 | 贵州省黔西南州同源高中2020-2021学年高二下学期期末考试数学(理)试题 (Word版含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 614.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 13:00:21 | ||
图片预览




文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
同源中学2020-2021学年度第二学期高二(理科)数学期末考试卷
第I卷(选择题)
一、单选题
1.已知集合,,则(
)
A.
B.
C.
D.
2.已知为虚数单位,则的共轭复数为(
)
A.
B.
C.
D.
3.若等差数列的前项和为,且,则的值为(
)
A.
B.
C.
D.
4.已知一个几何体的三视图及其大小如图,这个几何体的体积(
)
A.
B.
C.
D.
5.已知扇形面积为,半径是1,则扇形的圆心角是(
)
A.
B.
C.
D.
6.计算的值为
A.
B.
C.
D.
7.已知,,,则,,的大小是(
)
A.
B.
C.
D.
8.在中,角A,B,C所对的边分别为a,b,c,且,则角B的大小是(
)
A.45°
B.60°
C.90°
D.135°
9.执行右图所示的程序框图,则输出的值为(
)
A.
B.
C.
D.
10.已知某随机变量服从正态分布N(1,32),则P()为(
)(附:若随机变量服从正态分布N(,),则,)
A.87.22%
B.13.59%
C.27.18%
D.81.85%
11.2020年3月,中共中央国务院印发了《关于全面加强新时代大中小学劳动教育的意见》,提出“把劳动教育纳入人才培养全过程,贯通大中小学各学段,贯穿家庭?学校?社会各方面,与德育?智育?体育?美育相融合,紧密结合经济社会发展变化和学生生活实际,积极探索具有中国特色的劳动教育模式”.贵州省某学校结合自身实际,推出了《职业认知》《家政课程》《田地教育》《手工制作》《种植技术》五门劳动课程,要求学生从中任选两门进行学习,经考核合格后方能获得相应学分.已知甲?乙两人都选了《职业认知》,则另外一门课程不相同的概率为(
)
A.
B.
C.
D.
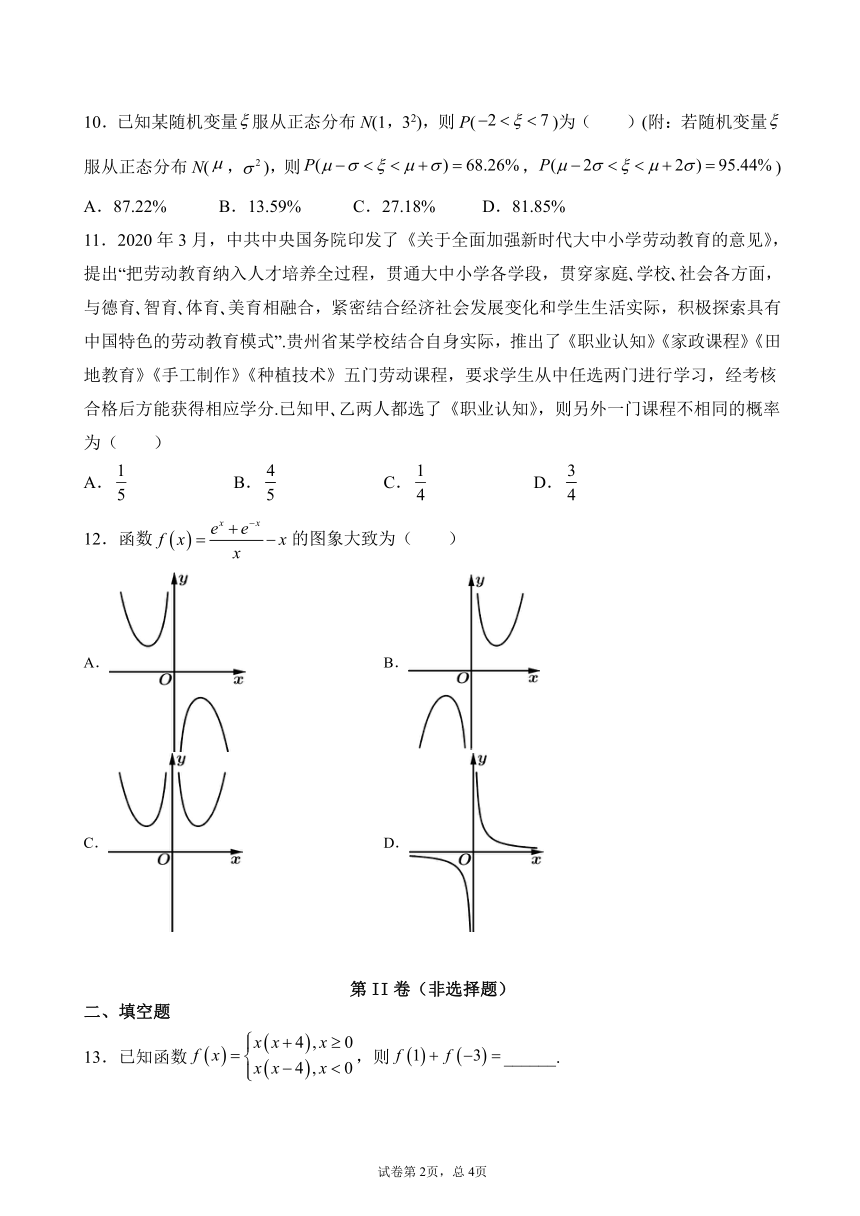
12.函数的图象大致为(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
13.已知函数,则______.
14.设,满足约束条件,则的最大值为________.
15.若的二项展开式中第5项为常数项,则______.
16.有下列五个命题:①函数的图像一定过定点;
②已知,且,则;
③
函数的定义域是,则函数的定义域为;
④已知且,则实数.
其中正确命题的序号是__________.(写出所有正确命题的序号)
三、解答题
17.记等差数列的前项和为,设,且成等比数列.
求
(1)
a1和d.
(2)求数列的前项和.
18.2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史
无接触史
总计
有武汉旅行史
27
无武汉旅行史
18
总计
27
54
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:
0.15
0.10
0.05
0.025
0.010
2.072
2.706
3.841
5.024
6.635
19.如图所示,平面ABCD,四边形AEFB为矩形,,,.
(1)求证:平面ADE;
(2)求平面CDF与平面AEFB所成锐二面角的余弦值.
20.已知椭圆:的左右焦点分别为和,为椭圆上的动点,的最小值为1,且的最大值为3.
(1)求椭圆的方程;
(2)若经过且倾斜角为45°的直线与椭圆交于、两点,求弦长.
21.已知函数
(1)求函数的单调区间;
(2)求函数的最小值
22.在直角坐标系中,直线l的参数方程是(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l和曲线C交于两点,点,求的值.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.B
【分析】
集合是确定的,需要计算集合,集合中的元素为,而函数的自变量是中的元素,将中的元素依次代入可以得到集合,根据集合的交集运算可得结果.
【详解】
∵,,
∴,
∴.
故选:B.
2.C
【分析】
利用复数的除法化简复数,利用共轭复数的定义可得结果.
【详解】
因为,因此,的共轭复数为.
故选:C.
3.B
【分析】
利用等差数列的前项和公式可求得的值.
【详解】
由等差数列的基本性质得,因此,.
故选:B.
【点睛】
本题考查等差数列求和,考查计算能力,属于基础题.
4.B
【分析】
根据三视图,还原出直观图,根据椎体和柱体的体积公式,即可得答案.
【详解】
由三视图可得,该几何体为一个底面半径为2,高为3的圆锥与一个底面半径为2,高为3的圆柱的组合体,
所以.
故选:B
5.C
【分析】
根据扇形面积公式即可求出.
【详解】
设扇形的圆心角为,
则,即,解得.
故选:C.
6.B
【分析】
将所求积分还原为,求解得到结果.
【详解】
本题正确选项:
【点睛】
本题考查积分的求解,属于基础题.
7.A
【分析】
利用中间量和比较可得答案.
【详解】
,,,
所以.
故选:A
【点睛】
关键点点睛:利用中间量和比较是解题关键.
8.A
【分析】
由利用余弦定理可得,结合的范围,即可得的值.
【详解】
中,,
可得:,
由余弦定理可得:
,
,
,
故选:A.
9.C
【分析】
按照程序框图运行程序即可求解.
【详解】
解:由程序框图可知:
第一次进入循环:,,
第二次进入循环:,,
第三次进入循环:,,
第四次进入循环:,,
此时,,终止循环,输出.
故选:C.
10.D
【分析】
由P(),结合所给条件,即可得解.
【详解】
因为p(-2<ξ<4)
,
p(-5<ξ<7)=
,
所以p(-2<ξ<7)=68.26%+(95.44%-68.26%)=81.85%,
故选:D.
11.D
【分析】
确定基本事件总数和满足题意的基本事件个数,由古典概型概率公式可得结果.
【详解】
由题意知:基本事件总数,
其中甲乙两人都选了《职业认知》,另外一门课程不相同所包含的基本事件个数,
甲?乙两人都选了《职业认知》,另外一门课程不相同的概率为:.
故选:D.
12.B
【分析】
利用奇偶性可排除C;令,利用导数可求得在上恒成立,由此可得在上恒成立,可排除A;利用洛必达法则知,可排除D,由此得到选项.
【详解】
由题意知:定义域为,
,
为奇函数,图象关于原点对称,可排除C;
令,则,,
当时,;当时,;
在上单调递减,在上单调递增,
,在上单调递增,
,
当时,,可排除A;
,,
由洛必达法则可知:,可排除D.
故选:B.
【点睛】
思路点睛:函数图象的辨识可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的特征点,排除不合要求的图象.
13.26
【分析】
代入分段函数,分别求值.
【详解】
,,
则.
故答案为:
14.
【分析】
作出可行域,平移目标函数找到取最大值的点,代入可求最大值.
【详解】
作出不等式组表示的可行域,如图,
设,由图可知,当直线经过点时,取到最大值,联立可得,代入可得取得最大值.
【点睛】
本题主要考查线性规划求解最值,作出可行域先确定最值点是求解关键,侧重考查直观想象,逻辑推理的核心素养.
15.6
【分析】
写出的展开式的通项,然后由题意可得当时的指数为0,从而解出.
【详解】
的展开式的通项为
因为展开式中第5项为常数项,所以,解得
故答案为:6
【点睛】
本题考查的是二项式定理,准确的写出通项是解题的关键,属于基础题.
16.①②④
【分析】
①根据函数的图像一定过定点可以直接判断;
②根据求出,然后计算即可判断;
③求抽象函数的定义域;
④指数与对数的互化,再结合对数的运算即可判断.
【详解】
①因为函数的图像一定过定点,
所以令,即,此时,
所以函数的图像一定过定点,故①正确;
②已知,且,即,
整理,而,故②正确;
③函数的定义域是,所以,即,
则函数的定义域为,故③错误;
④已知,则,
又,则,即,
所以,则实数,故④正确.
故答案为:①②④
17.(1),,或,,(2)或
【分析】
(1)由成等比数列,可得,结合,列出关于的方程组,可求出a1和d.
(2)直接利用等差数列的前项和公式求解即可
【详解】
解:(1)设等差数列的公差为,
因为成等比数列,所以,
即,
因为,所以,即,
所以,,解得或,
当时,,当时,,
所以,,或,,
(2)当,时,,
当,时,
【点睛】
此题考查了等差数列的通项公式和前项和公式,考查计算能力,属于基础题
18.(1)列联表见解析;(2)能
【分析】
(1)根据表格可得有武汉旅行史且有接触史的有9人,有武汉旅行史且无接触史的有18人,可以完成表格;
(2)根据列联表计算卡方,根据参考数据可以得出结论.
【详解】
(1)请将该列联表填写完整:
有接触史
无接触史
总计
有武汉旅行史
9
18
27
无武汉旅行史
18
9
27
总计
27
27
54
(2)根据列联表中的数据,由于
.
因此,在犯错误的概率不超过0.025的前提下,认为有武汉旅行史与有确诊病例接触史有关系.
【点睛】
本题主要考查独立性检验,题目较为简单,独立性检验根据公式计算卡方是求解的关键,侧重考查数据处理的核心素养.
19.(1)见解析(2)
【分析】
(1)根据,,从而证明平面平面ADE,从而平面ADE。(2)以A为坐标原点,建立空间直角坐标系,写出点的空间坐标,根据向量法求解即可。
【详解】
(1)∵四边形ABEF为矩形
又平面ADE,AE平面ADE
平面ADE
又,
同理可得:平面ADE
又,BF,BC
平面BCF
∴平面平面ADE
又CF平面BCF
平面ADE
(2)如图,以A为坐标原点,建立空间直角坐标系,则
,,
,,
设是平面CDF的一个法向量,则
即
令,解得
又是平面AEFB的一个法向量,
∴平面CDF与平面AEFB所成锐二面角的余弦值为.
【点睛】
此题考查立体几何线面平行证明和二面角求法,线面平行可先证面面平行得到,属于简单题目。
20.(1);(2)
【分析】
(1)由题可得,,即可求出,得出椭圆方程;
(2)求出直线方程,代入椭圆,写出韦达定理,利用弦长公式即可求出.
【详解】
(1)由题可知,当在左顶点时,取最小,取最大,
即,,解得,,
椭圆的方程为;
(2)可知直线斜率为1,且,
所以直线方程为,
设,
将直线方程代入椭圆方程可得,
,
.
21.(1)单调减区间是(-∞,,0),单调增区间是(0,+∞);(2)最小值1.
【分析】
(1)直接利用导数求函数的单调区间;
(2)由(1)可得ex≥x+1,当且仅当x=0时,等号成立,
把转化为,直接求出最小值1,并判断出g(x)取得最小值时条件存在.
【详解】
解∶(1)的定义域为R,
,
当x<0时,有,当x>0时,有;
所以函数f(x)的单调减区间是(-∞,,0),单调增区间是(0,+∞).
(2)由(1)可得f(x)min=f(0)=0,有ex≥x+1,当且仅当x=0时,等号成立,
所以,
当且仅当lnx+x=0时,等号成立.
设h(x)=lnx+x(x>0),
所以h(x)在(0,+∞)上是增函数,.
而,h(1)=1>0,
由零点存在性定理,存在唯一,使得h(x0)=0,
所以当x=x0时,函数g(x)取得最小值1.
【点睛】
导数的应用主要有:
(1)利用导函数几何意义求切线方程;
(2)利用导数研究原函数的单调性,求极值(最值);
(3)利用导数求参数的取值范围.
22.(1):,:;(2).
【分析】
(1)直接利用转换关系,在参数方程?极坐标方程和直角坐标方程之间进行转换;
(2)联立方程,利用韦达定理求出结果.
【详解】
(1)直线l的参数方程是(t为参数),转换为普通方程为.
曲线C的极坐标方程为,根据,转换为直角坐标方程为;
(2)把直线l的参数方程是(t为参数),代入,
得到,
所以,
所以.
答案第1页,总2页
答案第1页,总2页
同源中学2020-2021学年度第二学期高二(理科)数学期末考试卷
第I卷(选择题)
一、单选题
1.已知集合,,则(
)
A.
B.
C.
D.
2.已知为虚数单位,则的共轭复数为(
)
A.
B.
C.
D.
3.若等差数列的前项和为,且,则的值为(
)
A.
B.
C.
D.
4.已知一个几何体的三视图及其大小如图,这个几何体的体积(
)
A.
B.
C.
D.
5.已知扇形面积为,半径是1,则扇形的圆心角是(
)
A.
B.
C.
D.
6.计算的值为
A.
B.
C.
D.
7.已知,,,则,,的大小是(
)
A.
B.
C.
D.
8.在中,角A,B,C所对的边分别为a,b,c,且,则角B的大小是(
)
A.45°
B.60°
C.90°
D.135°
9.执行右图所示的程序框图,则输出的值为(
)
A.
B.
C.
D.
10.已知某随机变量服从正态分布N(1,32),则P()为(
)(附:若随机变量服从正态分布N(,),则,)
A.87.22%
B.13.59%
C.27.18%
D.81.85%
11.2020年3月,中共中央国务院印发了《关于全面加强新时代大中小学劳动教育的意见》,提出“把劳动教育纳入人才培养全过程,贯通大中小学各学段,贯穿家庭?学校?社会各方面,与德育?智育?体育?美育相融合,紧密结合经济社会发展变化和学生生活实际,积极探索具有中国特色的劳动教育模式”.贵州省某学校结合自身实际,推出了《职业认知》《家政课程》《田地教育》《手工制作》《种植技术》五门劳动课程,要求学生从中任选两门进行学习,经考核合格后方能获得相应学分.已知甲?乙两人都选了《职业认知》,则另外一门课程不相同的概率为(
)
A.
B.
C.
D.
12.函数的图象大致为(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题
13.已知函数,则______.
14.设,满足约束条件,则的最大值为________.
15.若的二项展开式中第5项为常数项,则______.
16.有下列五个命题:①函数的图像一定过定点;
②已知,且,则;
③
函数的定义域是,则函数的定义域为;
④已知且,则实数.
其中正确命题的序号是__________.(写出所有正确命题的序号)
三、解答题
17.记等差数列的前项和为,设,且成等比数列.
求
(1)
a1和d.
(2)求数列的前项和.
18.2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史
无接触史
总计
有武汉旅行史
27
无武汉旅行史
18
总计
27
54
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:
0.15
0.10
0.05
0.025
0.010
2.072
2.706
3.841
5.024
6.635
19.如图所示,平面ABCD,四边形AEFB为矩形,,,.
(1)求证:平面ADE;
(2)求平面CDF与平面AEFB所成锐二面角的余弦值.
20.已知椭圆:的左右焦点分别为和,为椭圆上的动点,的最小值为1,且的最大值为3.
(1)求椭圆的方程;
(2)若经过且倾斜角为45°的直线与椭圆交于、两点,求弦长.
21.已知函数
(1)求函数的单调区间;
(2)求函数的最小值
22.在直角坐标系中,直线l的参数方程是(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l和曲线C交于两点,点,求的值.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.B
【分析】
集合是确定的,需要计算集合,集合中的元素为,而函数的自变量是中的元素,将中的元素依次代入可以得到集合,根据集合的交集运算可得结果.
【详解】
∵,,
∴,
∴.
故选:B.
2.C
【分析】
利用复数的除法化简复数,利用共轭复数的定义可得结果.
【详解】
因为,因此,的共轭复数为.
故选:C.
3.B
【分析】
利用等差数列的前项和公式可求得的值.
【详解】
由等差数列的基本性质得,因此,.
故选:B.
【点睛】
本题考查等差数列求和,考查计算能力,属于基础题.
4.B
【分析】
根据三视图,还原出直观图,根据椎体和柱体的体积公式,即可得答案.
【详解】
由三视图可得,该几何体为一个底面半径为2,高为3的圆锥与一个底面半径为2,高为3的圆柱的组合体,
所以.
故选:B
5.C
【分析】
根据扇形面积公式即可求出.
【详解】
设扇形的圆心角为,
则,即,解得.
故选:C.
6.B
【分析】
将所求积分还原为,求解得到结果.
【详解】
本题正确选项:
【点睛】
本题考查积分的求解,属于基础题.
7.A
【分析】
利用中间量和比较可得答案.
【详解】
,,,
所以.
故选:A
【点睛】
关键点点睛:利用中间量和比较是解题关键.
8.A
【分析】
由利用余弦定理可得,结合的范围,即可得的值.
【详解】
中,,
可得:,
由余弦定理可得:
,
,
,
故选:A.
9.C
【分析】
按照程序框图运行程序即可求解.
【详解】
解:由程序框图可知:
第一次进入循环:,,
第二次进入循环:,,
第三次进入循环:,,
第四次进入循环:,,
此时,,终止循环,输出.
故选:C.
10.D
【分析】
由P(),结合所给条件,即可得解.
【详解】
因为p(-2<ξ<4)
,
p(-5<ξ<7)=
,
所以p(-2<ξ<7)=68.26%+(95.44%-68.26%)=81.85%,
故选:D.
11.D
【分析】
确定基本事件总数和满足题意的基本事件个数,由古典概型概率公式可得结果.
【详解】
由题意知:基本事件总数,
其中甲乙两人都选了《职业认知》,另外一门课程不相同所包含的基本事件个数,
甲?乙两人都选了《职业认知》,另外一门课程不相同的概率为:.
故选:D.
12.B
【分析】
利用奇偶性可排除C;令,利用导数可求得在上恒成立,由此可得在上恒成立,可排除A;利用洛必达法则知,可排除D,由此得到选项.
【详解】
由题意知:定义域为,
,
为奇函数,图象关于原点对称,可排除C;
令,则,,
当时,;当时,;
在上单调递减,在上单调递增,
,在上单调递增,
,
当时,,可排除A;
,,
由洛必达法则可知:,可排除D.
故选:B.
【点睛】
思路点睛:函数图象的辨识可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的特征点,排除不合要求的图象.
13.26
【分析】
代入分段函数,分别求值.
【详解】
,,
则.
故答案为:
14.
【分析】
作出可行域,平移目标函数找到取最大值的点,代入可求最大值.
【详解】
作出不等式组表示的可行域,如图,
设,由图可知,当直线经过点时,取到最大值,联立可得,代入可得取得最大值.
【点睛】
本题主要考查线性规划求解最值,作出可行域先确定最值点是求解关键,侧重考查直观想象,逻辑推理的核心素养.
15.6
【分析】
写出的展开式的通项,然后由题意可得当时的指数为0,从而解出.
【详解】
的展开式的通项为
因为展开式中第5项为常数项,所以,解得
故答案为:6
【点睛】
本题考查的是二项式定理,准确的写出通项是解题的关键,属于基础题.
16.①②④
【分析】
①根据函数的图像一定过定点可以直接判断;
②根据求出,然后计算即可判断;
③求抽象函数的定义域;
④指数与对数的互化,再结合对数的运算即可判断.
【详解】
①因为函数的图像一定过定点,
所以令,即,此时,
所以函数的图像一定过定点,故①正确;
②已知,且,即,
整理,而,故②正确;
③函数的定义域是,所以,即,
则函数的定义域为,故③错误;
④已知,则,
又,则,即,
所以,则实数,故④正确.
故答案为:①②④
17.(1),,或,,(2)或
【分析】
(1)由成等比数列,可得,结合,列出关于的方程组,可求出a1和d.
(2)直接利用等差数列的前项和公式求解即可
【详解】
解:(1)设等差数列的公差为,
因为成等比数列,所以,
即,
因为,所以,即,
所以,,解得或,
当时,,当时,,
所以,,或,,
(2)当,时,,
当,时,
【点睛】
此题考查了等差数列的通项公式和前项和公式,考查计算能力,属于基础题
18.(1)列联表见解析;(2)能
【分析】
(1)根据表格可得有武汉旅行史且有接触史的有9人,有武汉旅行史且无接触史的有18人,可以完成表格;
(2)根据列联表计算卡方,根据参考数据可以得出结论.
【详解】
(1)请将该列联表填写完整:
有接触史
无接触史
总计
有武汉旅行史
9
18
27
无武汉旅行史
18
9
27
总计
27
27
54
(2)根据列联表中的数据,由于
.
因此,在犯错误的概率不超过0.025的前提下,认为有武汉旅行史与有确诊病例接触史有关系.
【点睛】
本题主要考查独立性检验,题目较为简单,独立性检验根据公式计算卡方是求解的关键,侧重考查数据处理的核心素养.
19.(1)见解析(2)
【分析】
(1)根据,,从而证明平面平面ADE,从而平面ADE。(2)以A为坐标原点,建立空间直角坐标系,写出点的空间坐标,根据向量法求解即可。
【详解】
(1)∵四边形ABEF为矩形
又平面ADE,AE平面ADE
平面ADE
又,
同理可得:平面ADE
又,BF,BC
平面BCF
∴平面平面ADE
又CF平面BCF
平面ADE
(2)如图,以A为坐标原点,建立空间直角坐标系,则
,,
,,
设是平面CDF的一个法向量,则
即
令,解得
又是平面AEFB的一个法向量,
∴平面CDF与平面AEFB所成锐二面角的余弦值为.
【点睛】
此题考查立体几何线面平行证明和二面角求法,线面平行可先证面面平行得到,属于简单题目。
20.(1);(2)
【分析】
(1)由题可得,,即可求出,得出椭圆方程;
(2)求出直线方程,代入椭圆,写出韦达定理,利用弦长公式即可求出.
【详解】
(1)由题可知,当在左顶点时,取最小,取最大,
即,,解得,,
椭圆的方程为;
(2)可知直线斜率为1,且,
所以直线方程为,
设,
将直线方程代入椭圆方程可得,
,
.
21.(1)单调减区间是(-∞,,0),单调增区间是(0,+∞);(2)最小值1.
【分析】
(1)直接利用导数求函数的单调区间;
(2)由(1)可得ex≥x+1,当且仅当x=0时,等号成立,
把转化为,直接求出最小值1,并判断出g(x)取得最小值时条件存在.
【详解】
解∶(1)的定义域为R,
,
当x<0时,有,当x>0时,有;
所以函数f(x)的单调减区间是(-∞,,0),单调增区间是(0,+∞).
(2)由(1)可得f(x)min=f(0)=0,有ex≥x+1,当且仅当x=0时,等号成立,
所以,
当且仅当lnx+x=0时,等号成立.
设h(x)=lnx+x(x>0),
所以h(x)在(0,+∞)上是增函数,.
而,h(1)=1>0,
由零点存在性定理,存在唯一,使得h(x0)=0,
所以当x=x0时,函数g(x)取得最小值1.
【点睛】
导数的应用主要有:
(1)利用导函数几何意义求切线方程;
(2)利用导数研究原函数的单调性,求极值(最值);
(3)利用导数求参数的取值范围.
22.(1):,:;(2).
【分析】
(1)直接利用转换关系,在参数方程?极坐标方程和直角坐标方程之间进行转换;
(2)联立方程,利用韦达定理求出结果.
【详解】
(1)直线l的参数方程是(t为参数),转换为普通方程为.
曲线C的极坐标方程为,根据,转换为直角坐标方程为;
(2)把直线l的参数方程是(t为参数),代入,
得到,
所以,
所以.
答案第1页,总2页
答案第1页,总2页
同课章节目录
