25.1 概率(两课时)
图片预览

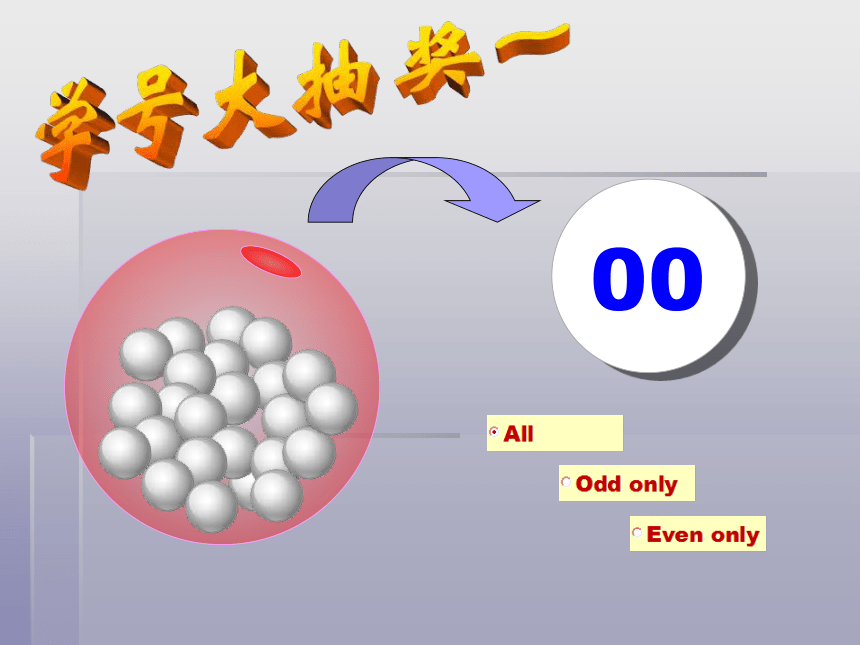





文档简介
(共37张PPT)
降水概率90%
第25章 概率初步
25.1 概率
第一课时
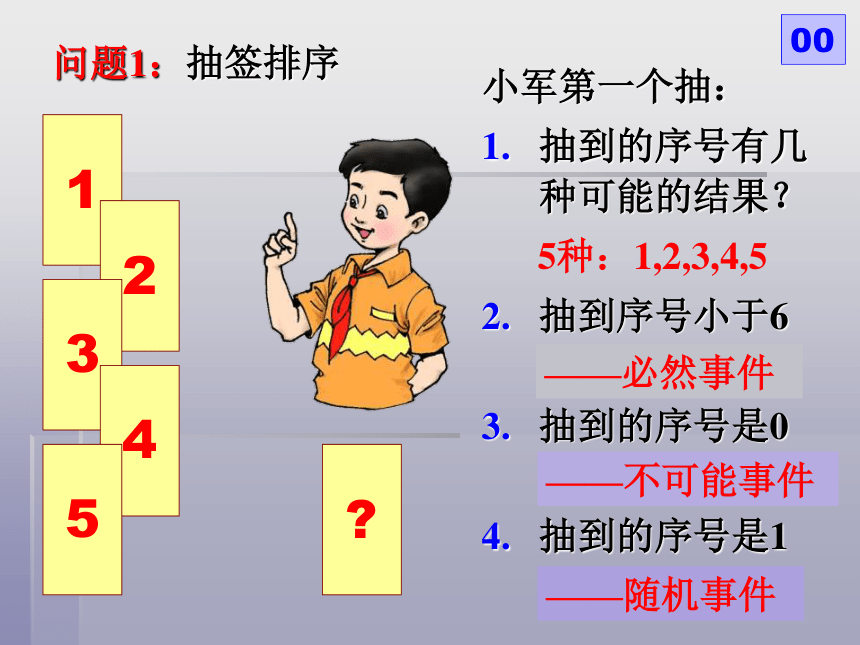
问题1:抽签排序
小军第一个抽:
抽到的序号有几种可能的结果?
5种:1,2,3,4,5
抽到序号小于6吗?
抽到的序号是0吗?
抽到的序号是1吗?
1
2
3
4
5
——必然事件
——不可能事件
——随机事件
1、随机事件
在一定条件下,可能发生也可能不发生的事件,称为随机事件。
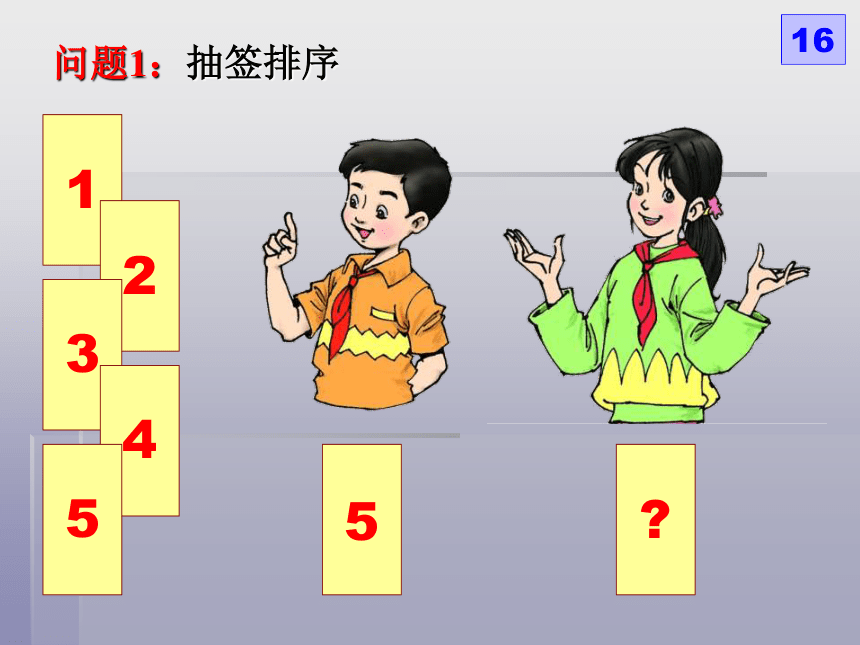
问题1:抽签排序
小军第一个抽:
抽到的序号有几种可能的结果?
5种:1,2,3,4,5
抽到序号小于6吗?
抽到的序号是0吗?
抽到的序号是1吗?
1
2
3
4
5
——必然事件
——不可能事件
——随机事件
问题1:抽签排序
1
2
3
4
5
练习1:下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件?说明理由。
篮球运动员在罚球线上投篮一次,未投中;
掷一次六面体骰子,向上的一面是6点;
度量三角形的内角和,结果是360°;
放学回家路上在每一个路口都遇上绿灯;
在标准大气压下,沸水的温度是100℃;
今晚打开电视发现在播广告;
将豆油滴在水中,豆油浮在水面上;
问题2:袋中摸球
袋子中有4个彩球和2个白球,这些球的形状、大小、质地完全相同。在看不到球的条件下,随机地从袋子中摸出一个球。
这个球是彩色还是白色?
摸出彩球和摸出白球的可能性一样大吗?
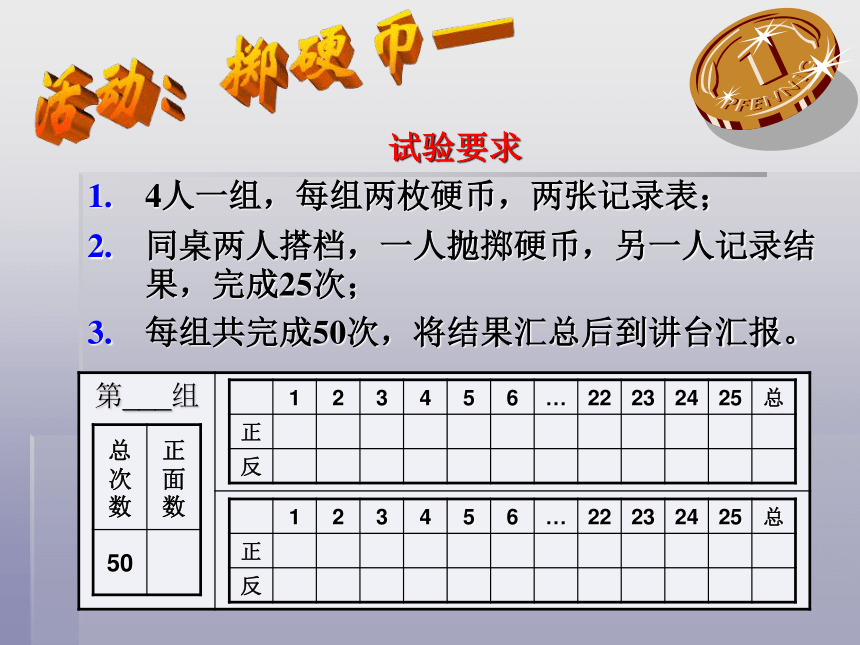
试验要求
4人一组,每组两枚硬币,两张记录表;
同桌两人搭档,一人抛掷硬币,另一人记录结果,完成25次;
每组共完成50次,将结果汇总后到讲台汇报。
第___组
总次数 正面数
50
1 2 3 4 5 6 … 22 23 24 25 总
正
反
1 2 3 4 5 6 … 22 23 24 25 总
正
反
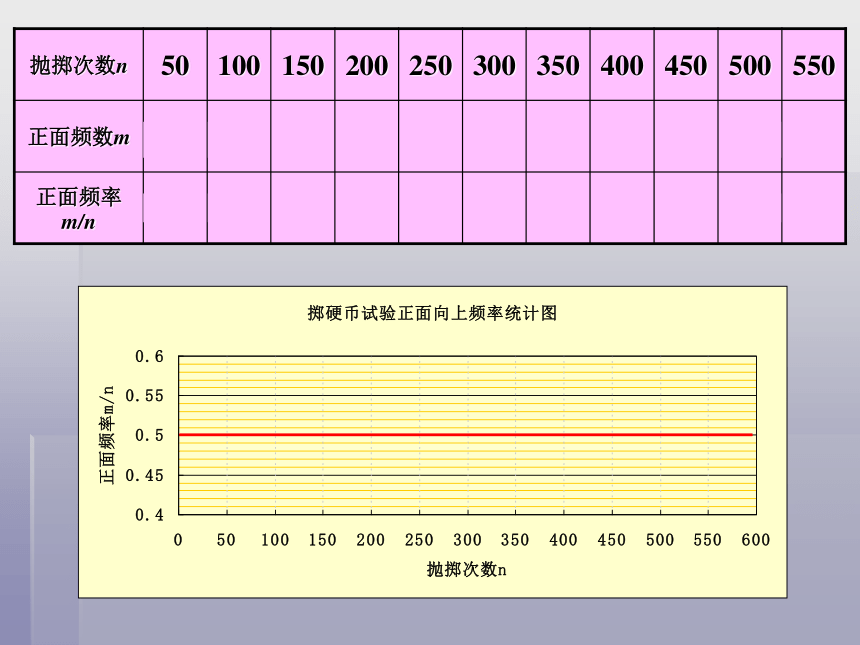
抛掷次数n 50 100 150 200 250 300 350 400 450 500 550
正面频数m
正面频率m/n
小组 1 2 3 4 5 6 7 8 9 10 11
总数 50 50 50 50 50 50 50 50 50 50 50
正面频数
抛掷次数n 50 100 150 200 250 300 350 400 450 500 550
正面频数m
正面频率m/n
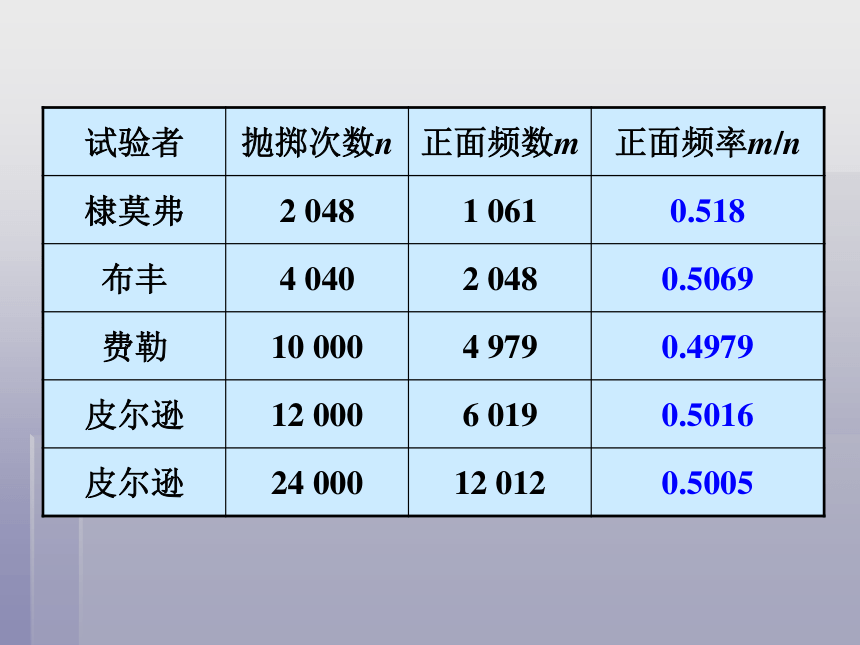
试验者 抛掷次数n 正面频数m 正面频率m/n
棣莫弗 2 048
布丰 4 040
费勒 10 000
皮尔逊 12 000
皮尔逊 24 000
1 061 0.518
2 048 0.5069
4 979 0.4979
6 019 0.5016
12 012 0.5005
观察试验结果, 随着抛掷次数的增加,“正面向上”的频率有怎样的规律?
抛掷次数n 正面频率m/n
2048 0.518
4040 0.5069
10000 0.4979
12000 0.5016
24000 0.5005
在大量重复抛掷硬币的试验中,“正面向上”发生的频率稳定在常数0.5附近,
那么就说抛掷硬币时“正面向上”的概率为0.5。
记为:P (正面向上) = 0.5.
2、概率的意义
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记为P(A)。
在大量重复试验中,如果事件A发生的频率 会稳定在某个常数 p 附近,那么这个常数 p 就叫做事件A的概率。
记为:P(A)=p.
2、概率的意义
由概率的意义可以知道:
0≤P(A)≤1
当A为必然事件时,P(A) =1
当A为不可能事件时, P(A) =0
试验者 抛掷次数n 正面频数m 正面频率m/n 正面向上
的概率
棣莫弗 2 048 1 061 0.518
布丰 4 040 2 048 0.5069
费勒 10 000 4 979 0.4979
皮尔逊 12 000 6 019 0.5016
皮尔逊 24 000 12 012 0.5005
P(正面向上) =0.5
30 000
练习2:在抛掷硬币的试验中,对于结论
P (正面向上)=0.5,判断以下解释是否正确:
对于每一次试验,有一半的可能是正面向上。
抛2次则必有1次是正面向上。
抛掷50次,如果大部分情况是正面向上的,则继续抛掷时反面向上的概率更大。
抛掷10次有可能都是反面向上。
如果连续抛掷了425次都是正面向上, 则对于第426次抛掷, P (正面向上) =P(反面向上)
√
×
×
√
√
练习3:某射击运动员在同一条件下的射击成绩记录如下:
计算表中相应的“射中9环以上”的频率(精确到0.01);
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1)?
射击次数 20 40 100 200 400 1000
射中9环以上次数 15 33 78 158 321 801
射中9环以上频率
从这堂课中你都学到了什么?
随机事件;
概率的意义;
频率与概率的关系。
小结:
Jocob Bernoulli
Jocob Bernoulli
无限地连续进行试验,我们终能正确地计算任何事物的概率,并从偶然现象之中看到事物的秩序。
——[瑞士]雅各布·伯努力
阅读思考: 生死签
相传古代有一小国,世代沿袭着一条奇特的法规:凡是死囚都要在临刑前当众抽一次“生死签”,即在两张纸条上分别写着“生”和“死”,抽到“死”签的立即斩首,抽到“生”签则当众释放。有一次,国王决定处死一个敢于“犯上”的大臣,于是勾结法官将两张纸条都写上“死”字……
如果你是这名囚臣,事先预料到了国王的阴谋,你会怎么做?
请用本课学习的知识来解读这则故事。
作业
试验探究:
小刚做掷硬币的游戏,得到结论:“掷两枚均匀的硬币,会出现三种情况:两正,一正一反,两反。所以出现一正一反的概率是1/3”。他的判断对吗?
先通过试验探索结论,再想想这是为什么?
作业
思索探讨: 彩票中的幸运号码
对于博彩,有这样两类观点:
一些人统计了每一期的中奖号码,认为中奖频率高的号码中奖的概率也高,因此倾向于选购这类高频号码;
还有一些人同样统计了每一期的中奖号码,但是他们知道,每个号码被抽中的概率是一样的,所以认为中奖次数少的号码更容易中奖,因此他们倾向于购买这类低频号码。
对于这两类互相矛盾的观点,你怎样看?
作业
第25章 概率初步
25.1 概率
第二课时
请看下面的几个试验:
试验1:从分别标有1,2,3,4,5,其它部分完全相同的5张卡片中随机的抽取一张。
结果有几种可能?
抽到1的概率有多大?
请看下面的几个试验:
试验2:掷一枚质地均匀的正方体骰子。
结果有几种可能?
向上的一面是6点的概率有多大?
请看下面的几个试验:
试验3:从一副扑克牌(54张)中随机抽出一张。
结果有几种可能?
抽到红桃2的概率有多大?
上面的试验有什么共同点?
归纳:可以发现以上试验都有两个共同特点:
1.每一次试验中,可能出现的结果只有有限个
2.每一次试验中,各种结果出现的可能性相等
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率:
古典概型
例1:掷一个质地均匀的正方体骰子,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5.
解:掷一个质地均匀的正方体骰子时,向上的一面的点数可能为_________,共__种,这些点数出现的可能性 _____。
(1)P(点数为2)=
(2)P(点数为奇数)=
(3)P(点数大于2且小于5)=
1,2,3,4,5,6
6
相等
1/6
3/6=1/2
2/6=1/3
例2:如图是一个转盘,转盘分成7个相同的扇形,颜色分为红、绿、黄三种颜色。指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形)。求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。
(1)摸出的球可能为什么颜色?
(2)每种情况出现的可能性相等吗?
(3)两者的概率分别为多少?
练习1:袋子中装有5个红球3个绿球,这些球除了颜色外都相同。从袋子中随机地摸出一个球,回答下列问题:
(1)抽到黑桃A;
(2)抽到红心;
(3)抽到10;
(4)抽到黑色牌。
练习2:从一副去掉大小王的扑克牌中任意抽出一张,求下列事件的概率:
(1)出现“5”的概率是多少?
(2)出现“6”的概率是多少?
(3)出现奇数的概率是多少?
练习3:(P132,习题25.1,4题)
一个质地均匀的小正方体,六个面分别标有数字“1”“1”“2”“4”“5”“5”。掷骰子后,观察朝上一面的数字。
练习4:(P132,习题25.1,5题)
如图是一个可以自由转动的没涂颜色的转盘,被分成12个相同的扇形。请你在转盘的适当地方涂上红、蓝两种颜色,使得转动的转盘自由停止时,指针指向红、蓝两色的概率分别为1/3,1/6.
思考题:三张卡片的骗局:
正
反
123
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率:
小结:
降水概率90%
第25章 概率初步
25.1 概率
第一课时
问题1:抽签排序
小军第一个抽:
抽到的序号有几种可能的结果?
5种:1,2,3,4,5
抽到序号小于6吗?
抽到的序号是0吗?
抽到的序号是1吗?
1
2
3
4
5
——必然事件
——不可能事件
——随机事件
1、随机事件
在一定条件下,可能发生也可能不发生的事件,称为随机事件。
问题1:抽签排序
小军第一个抽:
抽到的序号有几种可能的结果?
5种:1,2,3,4,5
抽到序号小于6吗?
抽到的序号是0吗?
抽到的序号是1吗?
1
2
3
4
5
——必然事件
——不可能事件
——随机事件
问题1:抽签排序
1
2
3
4
5
练习1:下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件?说明理由。
篮球运动员在罚球线上投篮一次,未投中;
掷一次六面体骰子,向上的一面是6点;
度量三角形的内角和,结果是360°;
放学回家路上在每一个路口都遇上绿灯;
在标准大气压下,沸水的温度是100℃;
今晚打开电视发现在播广告;
将豆油滴在水中,豆油浮在水面上;
问题2:袋中摸球
袋子中有4个彩球和2个白球,这些球的形状、大小、质地完全相同。在看不到球的条件下,随机地从袋子中摸出一个球。
这个球是彩色还是白色?
摸出彩球和摸出白球的可能性一样大吗?
试验要求
4人一组,每组两枚硬币,两张记录表;
同桌两人搭档,一人抛掷硬币,另一人记录结果,完成25次;
每组共完成50次,将结果汇总后到讲台汇报。
第___组
总次数 正面数
50
1 2 3 4 5 6 … 22 23 24 25 总
正
反
1 2 3 4 5 6 … 22 23 24 25 总
正
反
抛掷次数n 50 100 150 200 250 300 350 400 450 500 550
正面频数m
正面频率m/n
小组 1 2 3 4 5 6 7 8 9 10 11
总数 50 50 50 50 50 50 50 50 50 50 50
正面频数
抛掷次数n 50 100 150 200 250 300 350 400 450 500 550
正面频数m
正面频率m/n
试验者 抛掷次数n 正面频数m 正面频率m/n
棣莫弗 2 048
布丰 4 040
费勒 10 000
皮尔逊 12 000
皮尔逊 24 000
1 061 0.518
2 048 0.5069
4 979 0.4979
6 019 0.5016
12 012 0.5005
观察试验结果, 随着抛掷次数的增加,“正面向上”的频率有怎样的规律?
抛掷次数n 正面频率m/n
2048 0.518
4040 0.5069
10000 0.4979
12000 0.5016
24000 0.5005
在大量重复抛掷硬币的试验中,“正面向上”发生的频率稳定在常数0.5附近,
那么就说抛掷硬币时“正面向上”的概率为0.5。
记为:P (正面向上) = 0.5.
2、概率的意义
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记为P(A)。
在大量重复试验中,如果事件A发生的频率 会稳定在某个常数 p 附近,那么这个常数 p 就叫做事件A的概率。
记为:P(A)=p.
2、概率的意义
由概率的意义可以知道:
0≤P(A)≤1
当A为必然事件时,P(A) =1
当A为不可能事件时, P(A) =0
试验者 抛掷次数n 正面频数m 正面频率m/n 正面向上
的概率
棣莫弗 2 048 1 061 0.518
布丰 4 040 2 048 0.5069
费勒 10 000 4 979 0.4979
皮尔逊 12 000 6 019 0.5016
皮尔逊 24 000 12 012 0.5005
P(正面向上) =0.5
30 000
练习2:在抛掷硬币的试验中,对于结论
P (正面向上)=0.5,判断以下解释是否正确:
对于每一次试验,有一半的可能是正面向上。
抛2次则必有1次是正面向上。
抛掷50次,如果大部分情况是正面向上的,则继续抛掷时反面向上的概率更大。
抛掷10次有可能都是反面向上。
如果连续抛掷了425次都是正面向上, 则对于第426次抛掷, P (正面向上) =P(反面向上)
√
×
×
√
√
练习3:某射击运动员在同一条件下的射击成绩记录如下:
计算表中相应的“射中9环以上”的频率(精确到0.01);
根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1)?
射击次数 20 40 100 200 400 1000
射中9环以上次数 15 33 78 158 321 801
射中9环以上频率
从这堂课中你都学到了什么?
随机事件;
概率的意义;
频率与概率的关系。
小结:
Jocob Bernoulli
Jocob Bernoulli
无限地连续进行试验,我们终能正确地计算任何事物的概率,并从偶然现象之中看到事物的秩序。
——[瑞士]雅各布·伯努力
阅读思考: 生死签
相传古代有一小国,世代沿袭着一条奇特的法规:凡是死囚都要在临刑前当众抽一次“生死签”,即在两张纸条上分别写着“生”和“死”,抽到“死”签的立即斩首,抽到“生”签则当众释放。有一次,国王决定处死一个敢于“犯上”的大臣,于是勾结法官将两张纸条都写上“死”字……
如果你是这名囚臣,事先预料到了国王的阴谋,你会怎么做?
请用本课学习的知识来解读这则故事。
作业
试验探究:
小刚做掷硬币的游戏,得到结论:“掷两枚均匀的硬币,会出现三种情况:两正,一正一反,两反。所以出现一正一反的概率是1/3”。他的判断对吗?
先通过试验探索结论,再想想这是为什么?
作业
思索探讨: 彩票中的幸运号码
对于博彩,有这样两类观点:
一些人统计了每一期的中奖号码,认为中奖频率高的号码中奖的概率也高,因此倾向于选购这类高频号码;
还有一些人同样统计了每一期的中奖号码,但是他们知道,每个号码被抽中的概率是一样的,所以认为中奖次数少的号码更容易中奖,因此他们倾向于购买这类低频号码。
对于这两类互相矛盾的观点,你怎样看?
作业
第25章 概率初步
25.1 概率
第二课时
请看下面的几个试验:
试验1:从分别标有1,2,3,4,5,其它部分完全相同的5张卡片中随机的抽取一张。
结果有几种可能?
抽到1的概率有多大?
请看下面的几个试验:
试验2:掷一枚质地均匀的正方体骰子。
结果有几种可能?
向上的一面是6点的概率有多大?
请看下面的几个试验:
试验3:从一副扑克牌(54张)中随机抽出一张。
结果有几种可能?
抽到红桃2的概率有多大?
上面的试验有什么共同点?
归纳:可以发现以上试验都有两个共同特点:
1.每一次试验中,可能出现的结果只有有限个
2.每一次试验中,各种结果出现的可能性相等
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率:
古典概型
例1:掷一个质地均匀的正方体骰子,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5.
解:掷一个质地均匀的正方体骰子时,向上的一面的点数可能为_________,共__种,这些点数出现的可能性 _____。
(1)P(点数为2)=
(2)P(点数为奇数)=
(3)P(点数大于2且小于5)=
1,2,3,4,5,6
6
相等
1/6
3/6=1/2
2/6=1/3
例2:如图是一个转盘,转盘分成7个相同的扇形,颜色分为红、绿、黄三种颜色。指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形)。求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。
(1)摸出的球可能为什么颜色?
(2)每种情况出现的可能性相等吗?
(3)两者的概率分别为多少?
练习1:袋子中装有5个红球3个绿球,这些球除了颜色外都相同。从袋子中随机地摸出一个球,回答下列问题:
(1)抽到黑桃A;
(2)抽到红心;
(3)抽到10;
(4)抽到黑色牌。
练习2:从一副去掉大小王的扑克牌中任意抽出一张,求下列事件的概率:
(1)出现“5”的概率是多少?
(2)出现“6”的概率是多少?
(3)出现奇数的概率是多少?
练习3:(P132,习题25.1,4题)
一个质地均匀的小正方体,六个面分别标有数字“1”“1”“2”“4”“5”“5”。掷骰子后,观察朝上一面的数字。
练习4:(P132,习题25.1,5题)
如图是一个可以自由转动的没涂颜色的转盘,被分成12个相同的扇形。请你在转盘的适当地方涂上红、蓝两种颜色,使得转动的转盘自由停止时,指针指向红、蓝两色的概率分别为1/3,1/6.
思考题:三张卡片的骗局:
正
反
123
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率:
小结:
同课章节目录
