2021-2022学年鲁教版五四制七年级上册数学第二章 轴对称 基础夯实_单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教版五四制七年级上册数学第二章 轴对称 基础夯实_单元测试卷(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 521.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 17:32:41 | ||
图片预览




文档简介
第二章
轴对称
基础夯实—2021-2022学年鲁教版七年级上册数学单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.
1.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是(
)
A.
B.
C.
D.
2.如图与关于直线l对称,若,,则(
)
A.80°
B.65°
C.45°
D.35°
3.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图,一把直尺压住射线OB,另一把直尺压住射线OA,并且与第一把直尺交于点P,小明说:“射线OP就是的平分线.”他这样做的依据是(
)
A.角的内部到角的两边距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
4.如图,在由边长均为1的小正方形组成的网格上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,画法最多有(
)
A.1种
B.2种
C.3种
D.4种
5.如图,已知,点P在边OA上,,点M,N在边OB上,,若,则(
)
A.3
B.4
C.5
D.6
6.如图,在中,,的平分线交BC于点D,于点E.若,,则的面积为(
)
A.2.5
B.5
C.10
D.20
7.如图,和关于直线l对称,下列结论:
①;
②;
③直线l垂直平分线段;
④直线BC和的交点不一定在直线l上.
其中正确的有(
)
A.4个
B.3个
C.2个
D.1个
8.如图,在中,AC的垂直平分线分别交AC,BC于E,D两点,若,的周长为18,则的周长为(
)
A.12
B.14
C.16
D.18
9.如图,点A在直线MN上,点B在直线MN上方,点P为直线MN上一动点,当为等腰三角形时,则满足条件的点P的个数为(
)
A.1
B.3
C.4
D.5
10.如图,AD,CE分别是的中线和角平分线.若,,则的度数是(
)
A.20°
B.35°
C.40°
D.70°
二、填空题:本题共5小题,每小题5分,共25分.
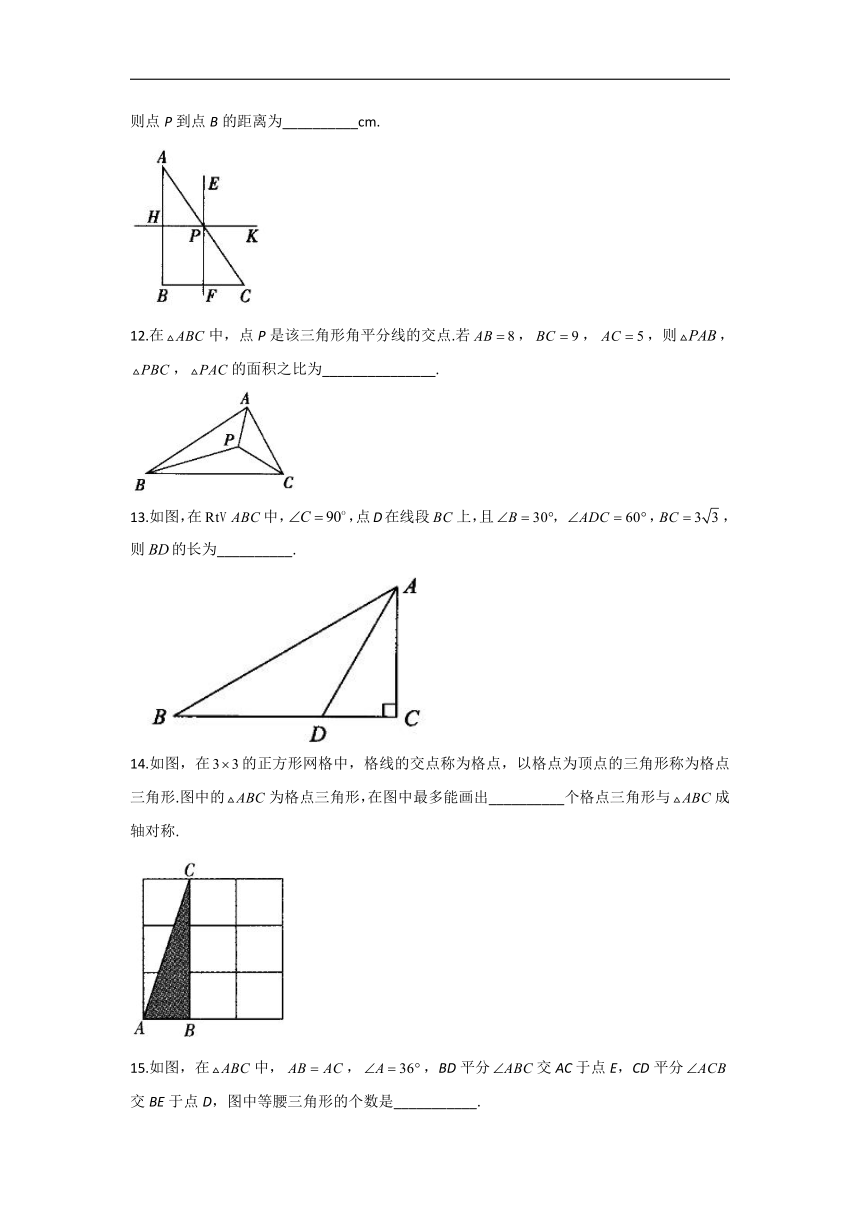
11.如图,线段AB的垂直平分线与BC的垂直平分线的交点P恰好在AC上,且cm,则点P到点B的距离为__________cm.
12.在中,点P是该三角形角平分线的交点.若,,,则,,的面积之比为_______________.
13.如图,在中,,点D在线段上,且,,则的长为__________.
14.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的为格点三角形,在图中最多能画出__________个格点三角形与成轴对称.
15.如图,在中,,,BD平分交AC于点E,CD平分交BE于点D,图中等腰三角形的个数是___________.
三、解答题:本题共2小题,第一小题10分,第二小题15分,共25分.
16.某班围棋兴趣小组的同学们在一次活动时用25粒围棋摆成了如图(1)所示的图案.甲、乙两人发现了该图案具有以下性质:
甲:这是一个轴对称图形,且有4条对称轴.
乙:这是一个轴对称图形,且每条对称轴都经过5粒棋子.
(1)请在图(2)中去掉4粒棋子,使所得图形仅保留甲所发现的性质.
(2)请在图(3)中去掉4粒棋子,使所得图形仅保留乙所发现的性质.
(3)在图(4)中,请去掉若干(大于0且小于10)粒棋子,使所得图形仍具有甲、乙两人所发现的所有性质.(在图中用“×”表示去掉的棋子)
17.如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
答案以及解析
1.答案:D
解析:A选项,是轴对称图形,故此选项不符合题意;B选项,是轴对称图形,故此选项不符合题意;C选项,是轴对称图形,故此选项不符合题意;D选项,不是轴对称图形,故此选项符合题意.故选D.
2.答案:D
解析:与关于直线l对称,,,.故选D.
3.答案:A
解析:如图所示,过两把直尺的交点P作,,两把长方形直尺完全相同,,又,,OP平分,依据是角的内部到角的两边距离相等的点在角的平分线上,故选A.
4.答案:D
解析:如图,共有4种画法.故选D.
5.答案:C
解析:如图,过点P作于点D.在中,,,,.,,,,.故选C.
6.答案:B
解析:在中,,的平分线交BC于点D,,,,,的面积为,故选B.
7.答案:B
解析:和关于直线l对称,,故①正确;,即,故②正确;直线l一定垂直平分线段,故③正确;根据对应线段或其延长线的交点在对称轴上可知④错误.综上所述,正确的结论有3个.故选B.
8.答案:A
解析:在中,AC的垂直平分线交AC于E,交BC于D,,.的周长是18,,,,的周长为12.故选A.
9.答案:C
解析:如图所示,分三种情况:①时,点P在AB的垂直平分线上,满足条件的点P有1个;②时,满足条件的点P有2个;③时,满足条件的点P有1个.综上所述,满足条件的点P有4个,故洗C.
10.答案:B
解析:先根据等腰三角形的性质及三角形内角和定理求出,,再利用角平分线的定义即可得出的度数.AD是的中线,,,,.CE是的角平分线,.故选B.
11.答案:5
解析:连接BP,利用线段垂直平分线的性质可得到,根据cm即可得出cm.
12.答案:
解析:根据角平分线的性质定理,得点P到的三边距离相等,从而得知,,的面积之比为.
13.答案:
解析:
在中,,,.
14.答案:6
解析:如图,最多能画出6个格点三角形与成轴对称.故答案为6.
15.答案:5
解析:,,是等腰三角形,.BD平分交AC于点E;.,是等腰三角形.,是等腰三角形.,是等腰三角形.,是等腰三角形,共有5个等腰三角形.
16.答案:(1)如图(1)所示.
(2)如图(2)所示.
(3)如图(3)所示.
17.答案:证明:(1),,
AM平分,DM平分,
,
,
,即.
(2)如图,过M作,垂足为点N,
,,
,,
AM平分,DM平分,
,,
,即M为BC的中点.
轴对称
基础夯实—2021-2022学年鲁教版七年级上册数学单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.
1.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是(
)
A.
B.
C.
D.
2.如图与关于直线l对称,若,,则(
)
A.80°
B.65°
C.45°
D.35°
3.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图,一把直尺压住射线OB,另一把直尺压住射线OA,并且与第一把直尺交于点P,小明说:“射线OP就是的平分线.”他这样做的依据是(
)
A.角的内部到角的两边距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
4.如图,在由边长均为1的小正方形组成的网格上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,画法最多有(
)
A.1种
B.2种
C.3种
D.4种
5.如图,已知,点P在边OA上,,点M,N在边OB上,,若,则(
)
A.3
B.4
C.5
D.6
6.如图,在中,,的平分线交BC于点D,于点E.若,,则的面积为(
)
A.2.5
B.5
C.10
D.20
7.如图,和关于直线l对称,下列结论:
①;
②;
③直线l垂直平分线段;
④直线BC和的交点不一定在直线l上.
其中正确的有(
)
A.4个
B.3个
C.2个
D.1个
8.如图,在中,AC的垂直平分线分别交AC,BC于E,D两点,若,的周长为18,则的周长为(
)
A.12
B.14
C.16
D.18
9.如图,点A在直线MN上,点B在直线MN上方,点P为直线MN上一动点,当为等腰三角形时,则满足条件的点P的个数为(
)
A.1
B.3
C.4
D.5
10.如图,AD,CE分别是的中线和角平分线.若,,则的度数是(
)
A.20°
B.35°
C.40°
D.70°
二、填空题:本题共5小题,每小题5分,共25分.
11.如图,线段AB的垂直平分线与BC的垂直平分线的交点P恰好在AC上,且cm,则点P到点B的距离为__________cm.
12.在中,点P是该三角形角平分线的交点.若,,,则,,的面积之比为_______________.
13.如图,在中,,点D在线段上,且,,则的长为__________.
14.如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的为格点三角形,在图中最多能画出__________个格点三角形与成轴对称.
15.如图,在中,,,BD平分交AC于点E,CD平分交BE于点D,图中等腰三角形的个数是___________.
三、解答题:本题共2小题,第一小题10分,第二小题15分,共25分.
16.某班围棋兴趣小组的同学们在一次活动时用25粒围棋摆成了如图(1)所示的图案.甲、乙两人发现了该图案具有以下性质:
甲:这是一个轴对称图形,且有4条对称轴.
乙:这是一个轴对称图形,且每条对称轴都经过5粒棋子.
(1)请在图(2)中去掉4粒棋子,使所得图形仅保留甲所发现的性质.
(2)请在图(3)中去掉4粒棋子,使所得图形仅保留乙所发现的性质.
(3)在图(4)中,请去掉若干(大于0且小于10)粒棋子,使所得图形仍具有甲、乙两人所发现的所有性质.(在图中用“×”表示去掉的棋子)
17.如图,四边形ABCD中,,,M为BC边上一点,且AM平分,DM平分.
求证:(1);
(2)M为BC的中点.
答案以及解析
1.答案:D
解析:A选项,是轴对称图形,故此选项不符合题意;B选项,是轴对称图形,故此选项不符合题意;C选项,是轴对称图形,故此选项不符合题意;D选项,不是轴对称图形,故此选项符合题意.故选D.
2.答案:D
解析:与关于直线l对称,,,.故选D.
3.答案:A
解析:如图所示,过两把直尺的交点P作,,两把长方形直尺完全相同,,又,,OP平分,依据是角的内部到角的两边距离相等的点在角的平分线上,故选A.
4.答案:D
解析:如图,共有4种画法.故选D.
5.答案:C
解析:如图,过点P作于点D.在中,,,,.,,,,.故选C.
6.答案:B
解析:在中,,的平分线交BC于点D,,,,,的面积为,故选B.
7.答案:B
解析:和关于直线l对称,,故①正确;,即,故②正确;直线l一定垂直平分线段,故③正确;根据对应线段或其延长线的交点在对称轴上可知④错误.综上所述,正确的结论有3个.故选B.
8.答案:A
解析:在中,AC的垂直平分线交AC于E,交BC于D,,.的周长是18,,,,的周长为12.故选A.
9.答案:C
解析:如图所示,分三种情况:①时,点P在AB的垂直平分线上,满足条件的点P有1个;②时,满足条件的点P有2个;③时,满足条件的点P有1个.综上所述,满足条件的点P有4个,故洗C.
10.答案:B
解析:先根据等腰三角形的性质及三角形内角和定理求出,,再利用角平分线的定义即可得出的度数.AD是的中线,,,,.CE是的角平分线,.故选B.
11.答案:5
解析:连接BP,利用线段垂直平分线的性质可得到,根据cm即可得出cm.
12.答案:
解析:根据角平分线的性质定理,得点P到的三边距离相等,从而得知,,的面积之比为.
13.答案:
解析:
在中,,,.
14.答案:6
解析:如图,最多能画出6个格点三角形与成轴对称.故答案为6.
15.答案:5
解析:,,是等腰三角形,.BD平分交AC于点E;.,是等腰三角形.,是等腰三角形.,是等腰三角形.,是等腰三角形,共有5个等腰三角形.
16.答案:(1)如图(1)所示.
(2)如图(2)所示.
(3)如图(3)所示.
17.答案:证明:(1),,
AM平分,DM平分,
,
,
,即.
(2)如图,过M作,垂足为点N,
,,
,,
AM平分,DM平分,
,,
,即M为BC的中点.
