2021—2022学年人教版八年级数学上册13.4 课题学习 最短路径问题 教学课件(共17张PPT)
文档属性
| 名称 | 2021—2022学年人教版八年级数学上册13.4 课题学习 最短路径问题 教学课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 18:16:54 | ||
图片预览





文档简介
(共17张PPT)
最短路径问题
学校:
教师:
最短路径问题:
是生活中的实际问题,在解决修路、铺管道等问题的时候可以起到节约人力、物力、财力的作用,这就需要把实际问题转化为数学问题来解决。
今天我们就通过几个实际问题学习如何设计最短路径。
相传,古希腊亚历山大里亚城有一位久负盛名的学者,名叫海伦。有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:
如图,从点A
地出发,到一条笔直的河边L饮马,然后到B
地,到河边的什么地方饮马,可使所走的路径最短?
精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题,这个问题后来被称为“将军饮马问题”。
A
B
l
导:
1.如图,连接A、B两点的所有连线中,哪条最短?
为什么?
A
B
①
②
③
②最短,因为两点之间,线段最短
2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?为什么?
P
l
A
B
C
D
PC最短,因为垂线段最短
知识回顾:
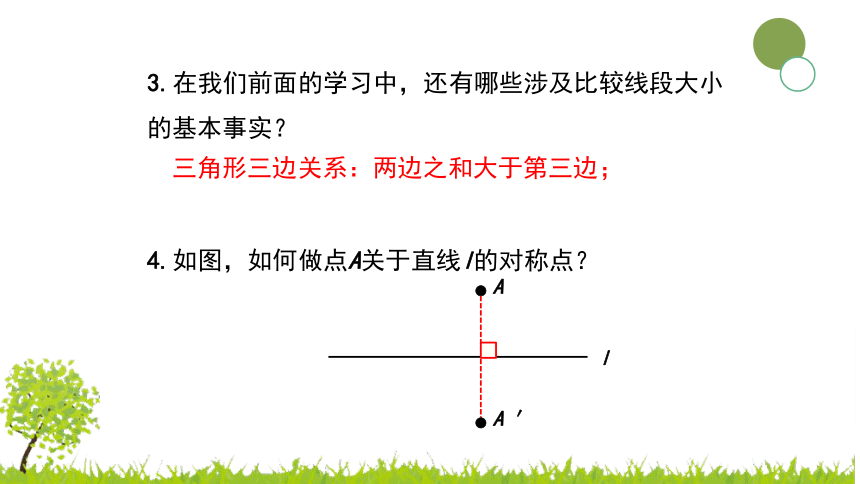
3.在我们前面的学习中,还有哪些涉及比较线段大小
的基本事实?
三角形三边关系:两边之和大于第三边;
4.如图,如何做点A关于直线l的对称点?
A
l
A
′
C
抽象成
A
B
l
数学问题
实际问题
A
B
l
作图:在直线l上求作一点C,使AC+BC最短问题.
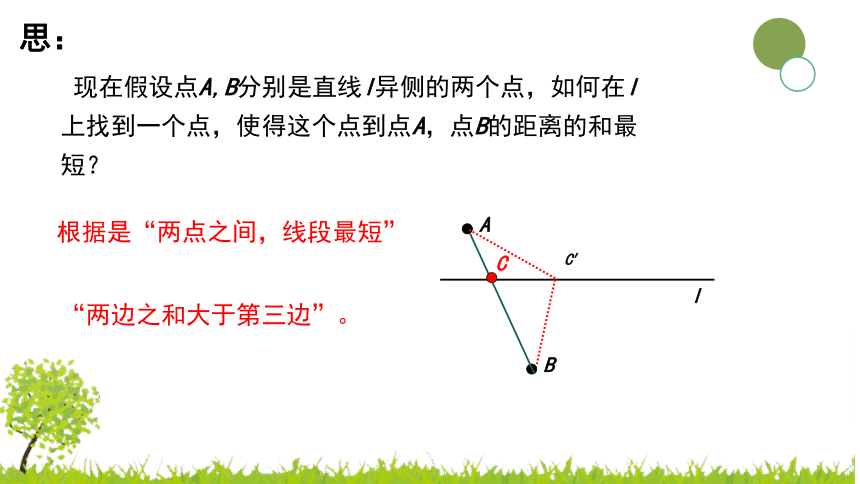
现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离的和最短?
A
l
B
C
根据是“两点之间,线段最短”
C′
思:
“两边之和大于第三边”。
问题
如果点A,B分别是直线l同侧的两个点,又应该如何解决?
思:1.如何把“同侧”转换“异侧”?
A
B
l
利用轴对称,作出点B关于直线l的对称点B′.
C
B
′
2.满足直线l
上的任意一点C,使CB
与CB′的长度相等?
3.在直线l上求作一点C,使AC+BC最短问题.
A
B
l
C′
C
B
′
议:你能用所学的知识证明AC
+BC最短吗?
证明:由轴对称的性质知,
BC
=B′C,BC′=B′C′.
∴ AC
+BC=
AC
+B′C
=
AB′,
∴
AC′+BC′=
AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴ AC
+BC<AC′+BC′.
即 AC
+BC
最短.
作法:
(1)作点B
关于直线l
的对称点B′;
(2)连接AB′,与直线l
相交于点C.
则点C
即为所求.
A
B
l
B
′
C
1.将“同侧”问题转换“异侧”问题;
2.利用的轴对称的性质将相等线段进行转换;
3.将求线段长的和转化为求某一线段的长。
方法总结:此类求线段和的最小值问题,找准对称点是关键,
变式1:
如图:M、N为
ABC边AB、AC上的两点,在BC上求作一点P,使
PMN的周长最小。
A
B
C
M
N
如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
F
A
O
B
D
·
·
C
E
G
H
变式2:
作法:
1.作点C关于直线
OA
的
对称点点F,
2.
作点D关于直线
OB
的对称点点E,
3.连接EF分别交直线OA.OB于点G.H,
则CG+GH+DH最短
限时练:
1.如图.P为
AOB内一点,P1,
P2分别是P关于OA,OB的对称点,交OA于点M,交OB于点N,若
P1
P2
=8cm.则
PMN的周长是(
).
O
A
B
P2
P1
P
M
N
A.7cm
B.5cm
C.8cm
D.10cm
2.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上一个动点,当
ABC的周长最小时,则求此时点C的坐标.
y
A
B
C
O
x
B
′
评:
这节课我们学习了哪些知识,运用了哪些数学思想?还存在哪些疑问?
本节课结束
同学们再见
最短路径问题
学校:
教师:
最短路径问题:
是生活中的实际问题,在解决修路、铺管道等问题的时候可以起到节约人力、物力、财力的作用,这就需要把实际问题转化为数学问题来解决。
今天我们就通过几个实际问题学习如何设计最短路径。
相传,古希腊亚历山大里亚城有一位久负盛名的学者,名叫海伦。有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:
如图,从点A
地出发,到一条笔直的河边L饮马,然后到B
地,到河边的什么地方饮马,可使所走的路径最短?
精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题,这个问题后来被称为“将军饮马问题”。
A
B
l
导:
1.如图,连接A、B两点的所有连线中,哪条最短?
为什么?
A
B
①
②
③
②最短,因为两点之间,线段最短
2.如图,点P是直线l外一点,点P与该直线l上各点连接的所有线段中,哪条最短?为什么?
P
l
A
B
C
D
PC最短,因为垂线段最短
知识回顾:
3.在我们前面的学习中,还有哪些涉及比较线段大小
的基本事实?
三角形三边关系:两边之和大于第三边;
4.如图,如何做点A关于直线l的对称点?
A
l
A
′
C
抽象成
A
B
l
数学问题
实际问题
A
B
l
作图:在直线l上求作一点C,使AC+BC最短问题.
现在假设点A,B分别是直线l异侧的两个点,如何在l上找到一个点,使得这个点到点A,点B的距离的和最短?
A
l
B
C
根据是“两点之间,线段最短”
C′
思:
“两边之和大于第三边”。
问题
如果点A,B分别是直线l同侧的两个点,又应该如何解决?
思:1.如何把“同侧”转换“异侧”?
A
B
l
利用轴对称,作出点B关于直线l的对称点B′.
C
B
′
2.满足直线l
上的任意一点C,使CB
与CB′的长度相等?
3.在直线l上求作一点C,使AC+BC最短问题.
A
B
l
C′
C
B
′
议:你能用所学的知识证明AC
+BC最短吗?
证明:由轴对称的性质知,
BC
=B′C,BC′=B′C′.
∴ AC
+BC=
AC
+B′C
=
AB′,
∴
AC′+BC′=
AC′+B′C′.
在△AB′C′中,
AB′<AC′+B′C′,
∴ AC
+BC<AC′+BC′.
即 AC
+BC
最短.
作法:
(1)作点B
关于直线l
的对称点B′;
(2)连接AB′,与直线l
相交于点C.
则点C
即为所求.
A
B
l
B
′
C
1.将“同侧”问题转换“异侧”问题;
2.利用的轴对称的性质将相等线段进行转换;
3.将求线段长的和转化为求某一线段的长。
方法总结:此类求线段和的最小值问题,找准对称点是关键,
变式1:
如图:M、N为
ABC边AB、AC上的两点,在BC上求作一点P,使
PMN的周长最小。
A
B
C
M
N
如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
F
A
O
B
D
·
·
C
E
G
H
变式2:
作法:
1.作点C关于直线
OA
的
对称点点F,
2.
作点D关于直线
OB
的对称点点E,
3.连接EF分别交直线OA.OB于点G.H,
则CG+GH+DH最短
限时练:
1.如图.P为
AOB内一点,P1,
P2分别是P关于OA,OB的对称点,交OA于点M,交OB于点N,若
P1
P2
=8cm.则
PMN的周长是(
).
O
A
B
P2
P1
P
M
N
A.7cm
B.5cm
C.8cm
D.10cm
2.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上一个动点,当
ABC的周长最小时,则求此时点C的坐标.
y
A
B
C
O
x
B
′
评:
这节课我们学习了哪些知识,运用了哪些数学思想?还存在哪些疑问?
本节课结束
同学们再见
