2021-2022学年苏科版数学九年级上册 2.4 圆周角(1)课件(共37张PPT)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级上册 2.4 圆周角(1)课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览






文档简介
(共37张PPT)
2.4
圆
周
角
老板
小陆,视频看了么
看了看了,好酷炫啊
我们现在接到任务,要为棕榈岛造一座桥
好的老板,我研究一下
已知:两灯塔与船的夹角是30°,棕榈岛可近似看成一个圆,半径是3千米,在两灯塔底部间修筑一桥梁,为方便准备材料,你能估算桥长吗?
情况说明
b
c
o
a
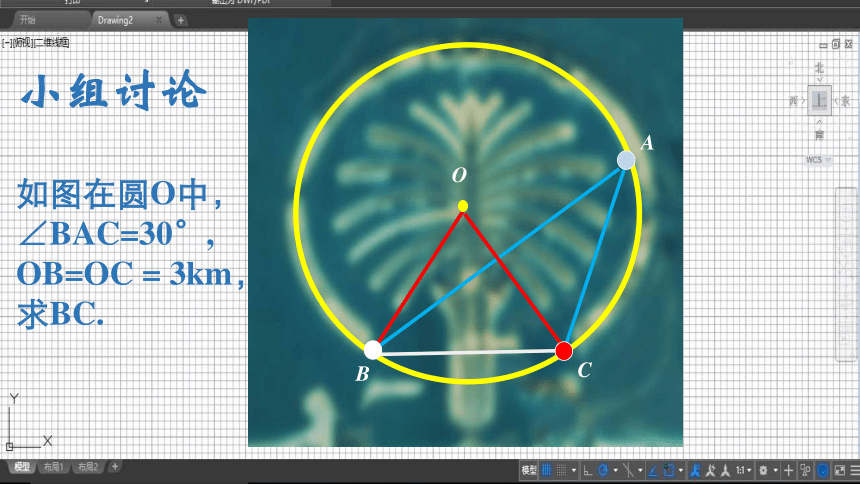
如图在圆O中,∠BAC=30°,
OB=OC
=
3km,求BC.
小组讨论
技术支持:
点与圆的位置关系
圆心角的概念
圆心角、弦、弧之间的相等关系
1
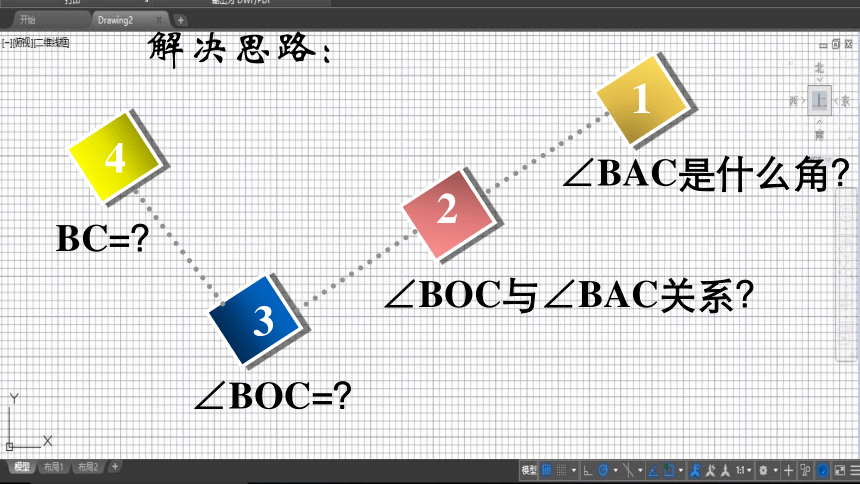
∠BAC是什么角?
解决思路:
2
3
4
∠BOC与∠BAC关系?
∠BOC=?
BC=?
b
c
d
e
o
a
b
c
d
a
o
e
圆周角的定义
o
b
c
a
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
⑴顶点在圆上
⑵角的两边和圆相交
特征:
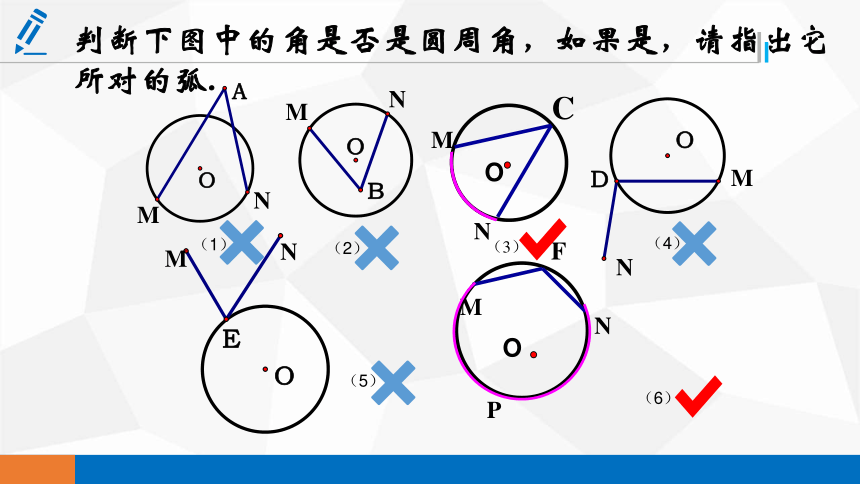
判断下图中的角是否是圆周角,如果是,请指出它所对的弧.
(1)
(2)
(3)
(4)
(5)
(6)
o
c
o
f
M
N
M
M
M
M
N
N
N
N
N
M
P
解决思路:
1
∠BAC是什么角?
2
3
4
∠BOC与∠BAC关系?
∠BOC=?
BC=?
∠BAC是圆周角
o
b
c
2.观察所画的圆周角,发现什么?
1.在⊙o中画出弧bc所对的圆心角和圆周角,你能
画出多少个符合条件的圆心角和圆周角?
探
索
圆心o与∠bac的位置关系
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
a
o
b
c
已知:⊙O中,
所对的圆周角是∠BAC,
圆心角是∠BOC.
求证:∠BAC=
∠BOC.
∵
OA=OC
∴
∠OCA=∠A
证明:
∵
∠BOC是△AOC的外角
∴
∠BOC=∠A+∠OCA=2∠A
即∠BAC=
∠BOC.
圆心o在∠bac的一边上
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
√
圆心O与∠BAC的位置关系
o
a
b
c
圆心o在∠bac的内部
d
o
a
b
d
o
a
c
d
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
√
圆心O与∠BAC的位置关系
√
c
a
b
o
d
c
a
o
d
a
b
o
d
c
a
b
o
d
圆心o在∠bac的外部
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
√
√
√
圆心o与∠bac的位置关系
o
a
b
c
d
p
q
若两条弧相等,则它们所对的圆心角有什么关系?所对的圆周角呢?
探
索
圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等.
圆周角定理:
o
b
c
a
d
e
解决思路:
1
2
3
4
∠BOC与∠BAC关系?
∠BOC=?
BC=?
∠BAC是圆周角
∠BOC=2∠BAC
已知:两灯塔与船的夹角是30°,棕榈岛可近似看成一个圆,半径是3千米,在两灯塔底部间修筑一桥梁,为方便准备材料,你能估算桥长吗?
解决思路:
1
2
3
4
∠BOC=?
BC=?
∠BAC是圆周角
∠BOC=2∠BAC
∠BOC=60°
BC=3
CCTV:哇,太棒啦,我要立刻报道!
BBC:确实厉害,一百个赞!
CNN:牛!但是我有个疑问。。。
b
c
d
a
o
e
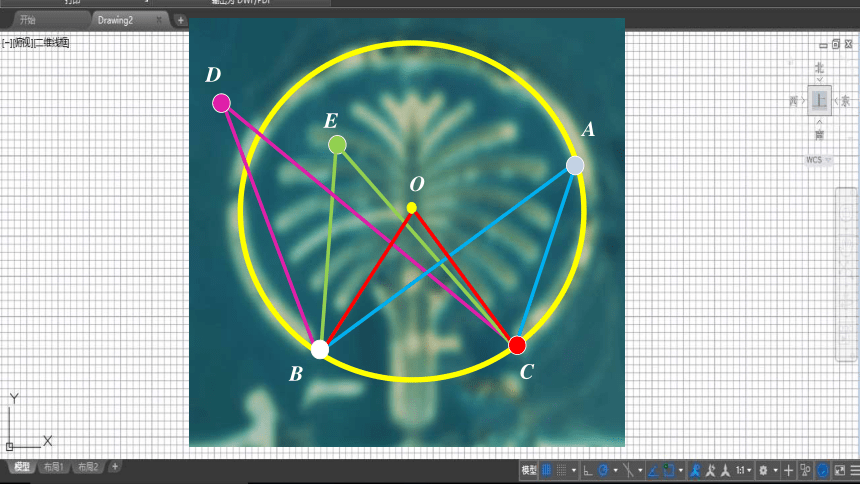
如图,∠D、∠E与∠A有怎样的大小关系?
老板老板,问题解决了
老板
非常好,你让小组成员赶紧打开PAD,又有新问题出现!
1.如图,○O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是(
)
A.
43°
B.
35°
C.
34°
D.44°
当堂反馈:
2.如图,在○O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为(
)
A.
30°
B.
35°
C.
34°
D.44°
3.如图,○O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为(
)
A
.
2
B.
1
C.
D.4
4.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是(
)度.
A
.
72
B.
108
C.
88
D.144
5.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为________.
老板,问题又解决了
老板
你组织大家总结下,这次技术上有哪些新的进展?
1组:过程中用到了分类讨论,从特殊到一般的思想
2组:同弧或等弧所对的圆周角相等
3组:学到一类新的角:圆周角
5组:还用到了转化、化归的思想
4组:圆周角的度数等于它所对弧上的圆心角度数的一半
如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE//AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECO为平行四边形
(2)连接CO,求证:CO平分∠BCE
拓展延伸:
2.4
圆
周
角
老板
小陆,视频看了么
看了看了,好酷炫啊
我们现在接到任务,要为棕榈岛造一座桥
好的老板,我研究一下
已知:两灯塔与船的夹角是30°,棕榈岛可近似看成一个圆,半径是3千米,在两灯塔底部间修筑一桥梁,为方便准备材料,你能估算桥长吗?
情况说明
b
c
o
a
如图在圆O中,∠BAC=30°,
OB=OC
=
3km,求BC.
小组讨论
技术支持:
点与圆的位置关系
圆心角的概念
圆心角、弦、弧之间的相等关系
1
∠BAC是什么角?
解决思路:
2
3
4
∠BOC与∠BAC关系?
∠BOC=?
BC=?
b
c
d
e
o
a
b
c
d
a
o
e
圆周角的定义
o
b
c
a
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
⑴顶点在圆上
⑵角的两边和圆相交
特征:
判断下图中的角是否是圆周角,如果是,请指出它所对的弧.
(1)
(2)
(3)
(4)
(5)
(6)
o
c
o
f
M
N
M
M
M
M
N
N
N
N
N
M
P
解决思路:
1
∠BAC是什么角?
2
3
4
∠BOC与∠BAC关系?
∠BOC=?
BC=?
∠BAC是圆周角
o
b
c
2.观察所画的圆周角,发现什么?
1.在⊙o中画出弧bc所对的圆心角和圆周角,你能
画出多少个符合条件的圆心角和圆周角?
探
索
圆心o与∠bac的位置关系
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
a
o
b
c
已知:⊙O中,
所对的圆周角是∠BAC,
圆心角是∠BOC.
求证:∠BAC=
∠BOC.
∵
OA=OC
∴
∠OCA=∠A
证明:
∵
∠BOC是△AOC的外角
∴
∠BOC=∠A+∠OCA=2∠A
即∠BAC=
∠BOC.
圆心o在∠bac的一边上
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
√
圆心O与∠BAC的位置关系
o
a
b
c
圆心o在∠bac的内部
d
o
a
b
d
o
a
c
d
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
√
圆心O与∠BAC的位置关系
√
c
a
b
o
d
c
a
o
d
a
b
o
d
c
a
b
o
d
圆心o在∠bac的外部
圆心o在∠bac的一边上
圆心o在∠bac的内部
圆心o在∠bac的外部
(1)
(2)
(3)
o
a
b
c
a
o
b
c
c
a
b
o
√
√
√
圆心o与∠bac的位置关系
o
a
b
c
d
p
q
若两条弧相等,则它们所对的圆心角有什么关系?所对的圆周角呢?
探
索
圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等.
圆周角定理:
o
b
c
a
d
e
解决思路:
1
2
3
4
∠BOC与∠BAC关系?
∠BOC=?
BC=?
∠BAC是圆周角
∠BOC=2∠BAC
已知:两灯塔与船的夹角是30°,棕榈岛可近似看成一个圆,半径是3千米,在两灯塔底部间修筑一桥梁,为方便准备材料,你能估算桥长吗?
解决思路:
1
2
3
4
∠BOC=?
BC=?
∠BAC是圆周角
∠BOC=2∠BAC
∠BOC=60°
BC=3
CCTV:哇,太棒啦,我要立刻报道!
BBC:确实厉害,一百个赞!
CNN:牛!但是我有个疑问。。。
b
c
d
a
o
e
如图,∠D、∠E与∠A有怎样的大小关系?
老板老板,问题解决了
老板
非常好,你让小组成员赶紧打开PAD,又有新问题出现!
1.如图,○O中,弦AB、CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是(
)
A.
43°
B.
35°
C.
34°
D.44°
当堂反馈:
2.如图,在○O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为(
)
A.
30°
B.
35°
C.
34°
D.44°
3.如图,○O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为(
)
A
.
2
B.
1
C.
D.4
4.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是(
)度.
A
.
72
B.
108
C.
88
D.144
5.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为________.
老板,问题又解决了
老板
你组织大家总结下,这次技术上有哪些新的进展?
1组:过程中用到了分类讨论,从特殊到一般的思想
2组:同弧或等弧所对的圆周角相等
3组:学到一类新的角:圆周角
5组:还用到了转化、化归的思想
4组:圆周角的度数等于它所对弧上的圆心角度数的一半
如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE//AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECO为平行四边形
(2)连接CO,求证:CO平分∠BCE
拓展延伸:
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
