沪教版(五四学制)六上4.1圆的周长 课件(40张)
文档属性
| 名称 | 沪教版(五四学制)六上4.1圆的周长 课件(40张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
教学目标
1.
理解圆周率的意义,推导出圆周长的计算公式,并能正确地进行简单计算。
2.
使同学们经历圆的周长的推导过程,培养同学们的观察、比较、分析、综合及动手操作能力。
3.
领会事物之间是联系和发展的辨证唯物主义观念;结合圆周率的学习,对学生进行爱国主义教育。
1、圆的周长公式:
C=
πd
d
=
C
÷π
或C=2π
r
r
=
C
÷π÷2
2、在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。
3、区分周长的一半和半圆的周长:
(1)周长的一半:等于圆的周长÷2
计算方法:2π
r
÷
2
即
C=π
r
(2)半圆的周长:等于圆的周长的一半加直径。
计算方法:C半圆=πd÷
2+d
C半圆=πr+2r
4、用转化的方法解决组合图形的周长问题。
1.运用圆的周长公式解决稍复杂的与圆相关的组合图形的周长问题。
2.渗透转化的方法解决实际问题。
运用圆的周长公式解决生活中的实际问题。
把圆的周长的计算公式与实际问题很好的连接在一起,解决要求的实际问题。
点O是这个圆的
;
线段OP是这个圆的
;
线段AB是这个圆的
;
OP和AB存在怎样的数量关系?
圆心
半径
直径
d=2r
或者
r=d÷2
?3
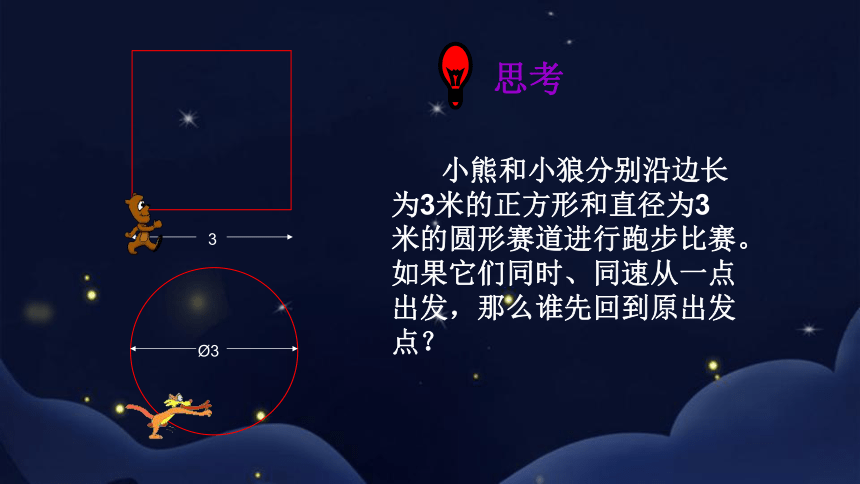
思考
小熊和小狼分别沿边长为3米的正方形和直径为3米的圆形赛道进行跑步比赛。如果它们同时、同速从一点出发,那么谁先回到原出发点?
3
思考
操作1
操作2
周长C
直径d
C与d的比值
(1)
(2)
圆的周长÷直径=定值
π
对于圆周率的研究,我国古代数学家曾取得了辉煌的成就。魏晋时代的数学家刘徽首创了“割圆术”,求得的近似值为3.1416。南北朝时代的数学家祖冲之将圆周率精确到了3.1415926和3.1415927之间。比德国数学家奥托整整早了一千多年。
刘徽
祖冲之
比赛
例1
一张王莲的叶子近似于一个圆,它的直径约是0.95米。这张叶子的周长是多少米?(结果保留两位小数)
巩固练习
求下列圆的周长
2
r=4m
1
d=30cm
例2
一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
O
6400
解 R轨=500+6400=6900,
C轨=2πR轨=2×3.14×6900=43332
14C轨=43332×14=606648(千米)
答:卫星围绕地球一共飞行了约606648千米。
例2
一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
O
例3
如图,如果圆环的外圆周长
C1=628cm,内圆周长C2=314cm,求圆环的宽度d。
d
O
解 由C=2πR=2×3.14×R=6.28×R,得R=C÷6.28
设外圆的半径为R1,内圆的半径为R2,则
R1=C1÷6.28,R2=C2÷6.28,
d=R1-R2=(C1-C2)÷6.28
=(628-314)÷6.28
=50(cm)
答:圆环的宽度是50cm。
R1
R2
练习1
右图是一个由半圆和一条直径所组成的图形,求这个图形的周长,小明、小丽和小杰谁算得对?为什么?(单位:厘米)
?5
小明:3.14×5+5
小丽:3.14×5÷2
小杰:3.14×5÷2+5
(√)
练习2
为了迎接2008年奥运会,北京某体育场新建一环行跑道(如图),求此环行跑道的周长是多少米?
这辆自行车后轮转一圈,大约可以走多远?小明家离学校1km,后轮转480圈够吗?
2×3.14×33=207.24(cm)≈
2.07(m)
1000÷2.07
≈483(圈)
1
km=1000
m
答:这辆自行车后轮转一圈,大约可以走2.07m。小明从家到学校,后轮转480圈不够。
C=2πr
用转化的方法解决组合图形的周长问题。
求阴影部分的周长。
阴影部分的图形不规则,该如何计算呢?
A
B
阴影部分的周长=
大半圆的周长
+
圆A的周长+
圆B的周长
3.14×(3+5)÷2=12.56
3.14×3÷2=4.71
3.14×5÷2=7.85
12.56+4.71+7.85=25.12
答:阴影部分的周长为25.12。
用转化的方法解决捆扎物体的周长问题。
直径均为1dm的4根管子被一根金属带紧紧地捆在一起,如下图。求金属带的长度。
可以把求金属带的长度转化成求一个圆的周长加上4条直径的长度和。
3.14×1+4×1=7.14(dm)
答:金属带的长度为7.14dm。
1.一个街心花园的形状如下图所示,中间正
方形的边长为20m,四周是半圆,这个街
心花园的周长是多少米?
3.14×20×2=125.6(米)
答:这个街心花园的周长是125.6米。
2.计算下面阴影部分的周长。
5cm
3.14×10÷2+3.14×5
=31.4(cm)
1.有几棵二百多年的银杏树,我想知道它们的横截面的直径,应当怎么办?
2.小熊和小狼同时从同一点出发进行比赛,小熊走外面的大圆,小狼沿“8”字型走里面的两个小圆,如果它们的速度相同,谁先回到出发点?
返回
返回
返回
用转化的方法解决
组合图形的周长问题
捆扎物体的周长问题
教学目标
1.
理解圆周率的意义,推导出圆周长的计算公式,并能正确地进行简单计算。
2.
使同学们经历圆的周长的推导过程,培养同学们的观察、比较、分析、综合及动手操作能力。
3.
领会事物之间是联系和发展的辨证唯物主义观念;结合圆周率的学习,对学生进行爱国主义教育。
1、圆的周长公式:
C=
πd
d
=
C
÷π
或C=2π
r
r
=
C
÷π÷2
2、在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
在一个长方形里画一个最大的圆,圆的直径等于长方形的宽。
3、区分周长的一半和半圆的周长:
(1)周长的一半:等于圆的周长÷2
计算方法:2π
r
÷
2
即
C=π
r
(2)半圆的周长:等于圆的周长的一半加直径。
计算方法:C半圆=πd÷
2+d
C半圆=πr+2r
4、用转化的方法解决组合图形的周长问题。
1.运用圆的周长公式解决稍复杂的与圆相关的组合图形的周长问题。
2.渗透转化的方法解决实际问题。
运用圆的周长公式解决生活中的实际问题。
把圆的周长的计算公式与实际问题很好的连接在一起,解决要求的实际问题。
点O是这个圆的
;
线段OP是这个圆的
;
线段AB是这个圆的
;
OP和AB存在怎样的数量关系?
圆心
半径
直径
d=2r
或者
r=d÷2
?3
思考
小熊和小狼分别沿边长为3米的正方形和直径为3米的圆形赛道进行跑步比赛。如果它们同时、同速从一点出发,那么谁先回到原出发点?
3
思考
操作1
操作2
周长C
直径d
C与d的比值
(1)
(2)
圆的周长÷直径=定值
π
对于圆周率的研究,我国古代数学家曾取得了辉煌的成就。魏晋时代的数学家刘徽首创了“割圆术”,求得的近似值为3.1416。南北朝时代的数学家祖冲之将圆周率精确到了3.1415926和3.1415927之间。比德国数学家奥托整整早了一千多年。
刘徽
祖冲之
比赛
例1
一张王莲的叶子近似于一个圆,它的直径约是0.95米。这张叶子的周长是多少米?(结果保留两位小数)
巩固练习
求下列圆的周长
2
r=4m
1
d=30cm
例2
一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
O
6400
解 R轨=500+6400=6900,
C轨=2πR轨=2×3.14×6900=43332
14C轨=43332×14=606648(千米)
答:卫星围绕地球一共飞行了约606648千米。
例2
一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
O
例3
如图,如果圆环的外圆周长
C1=628cm,内圆周长C2=314cm,求圆环的宽度d。
d
O
解 由C=2πR=2×3.14×R=6.28×R,得R=C÷6.28
设外圆的半径为R1,内圆的半径为R2,则
R1=C1÷6.28,R2=C2÷6.28,
d=R1-R2=(C1-C2)÷6.28
=(628-314)÷6.28
=50(cm)
答:圆环的宽度是50cm。
R1
R2
练习1
右图是一个由半圆和一条直径所组成的图形,求这个图形的周长,小明、小丽和小杰谁算得对?为什么?(单位:厘米)
?5
小明:3.14×5+5
小丽:3.14×5÷2
小杰:3.14×5÷2+5
(√)
练习2
为了迎接2008年奥运会,北京某体育场新建一环行跑道(如图),求此环行跑道的周长是多少米?
这辆自行车后轮转一圈,大约可以走多远?小明家离学校1km,后轮转480圈够吗?
2×3.14×33=207.24(cm)≈
2.07(m)
1000÷2.07
≈483(圈)
1
km=1000
m
答:这辆自行车后轮转一圈,大约可以走2.07m。小明从家到学校,后轮转480圈不够。
C=2πr
用转化的方法解决组合图形的周长问题。
求阴影部分的周长。
阴影部分的图形不规则,该如何计算呢?
A
B
阴影部分的周长=
大半圆的周长
+
圆A的周长+
圆B的周长
3.14×(3+5)÷2=12.56
3.14×3÷2=4.71
3.14×5÷2=7.85
12.56+4.71+7.85=25.12
答:阴影部分的周长为25.12。
用转化的方法解决捆扎物体的周长问题。
直径均为1dm的4根管子被一根金属带紧紧地捆在一起,如下图。求金属带的长度。
可以把求金属带的长度转化成求一个圆的周长加上4条直径的长度和。
3.14×1+4×1=7.14(dm)
答:金属带的长度为7.14dm。
1.一个街心花园的形状如下图所示,中间正
方形的边长为20m,四周是半圆,这个街
心花园的周长是多少米?
3.14×20×2=125.6(米)
答:这个街心花园的周长是125.6米。
2.计算下面阴影部分的周长。
5cm
3.14×10÷2+3.14×5
=31.4(cm)
1.有几棵二百多年的银杏树,我想知道它们的横截面的直径,应当怎么办?
2.小熊和小狼同时从同一点出发进行比赛,小熊走外面的大圆,小狼沿“8”字型走里面的两个小圆,如果它们的速度相同,谁先回到出发点?
返回
返回
返回
用转化的方法解决
组合图形的周长问题
捆扎物体的周长问题
