沪教版(五四学制)六上3.2 比的基本性质 课件(21张)
文档属性
| 名称 | 沪教版(五四学制)六上3.2 比的基本性质 课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 16:06:17 | ||
图片预览






文档简介
(共21张PPT)
3.2
比
的
基
本
性
质
13÷18=
(
)
(
)
=
(
):
(
)
除法
分数
比
13
18
13
18
前项
:(比号)
后项
比值
分子
_____
(分数线)
分母
分数值
被除数
÷(除号)
除数
商
记忆宝库
在括号里填上适当的数,
使等式成立
80÷10=800÷(
)=(
)÷5
100
40
3
4
=
(
)
16
=
6
(
)
12
8
填空:
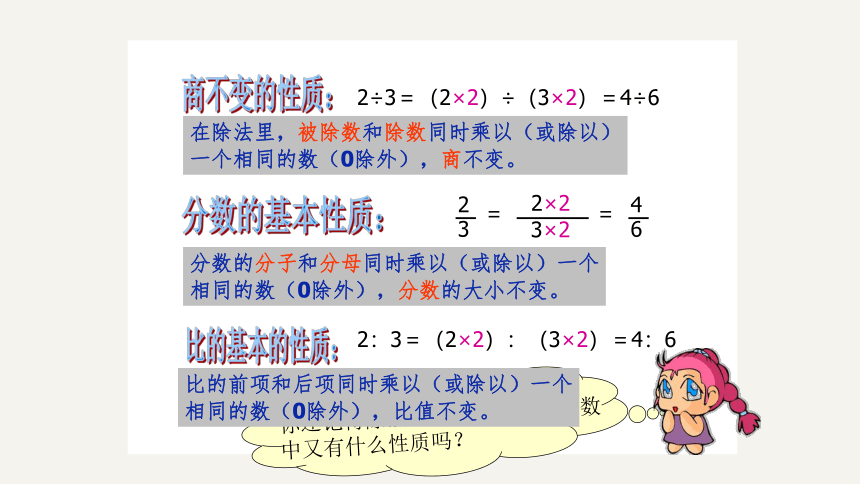
你还记得除法中有什么性质?分数中又有什么性质吗?
商不变的性质:
分数的基本性质:
2÷3=(2×2)÷(3×2)=4÷6
3
2
2×2
3×2
6
4
=
=
在除法里,被除数和除数同时乘以(或除以)
一个相同的数(0除外),商不变。
分数的分子和分母同时乘以(或除以)一个
相同的数(0除外),分数的大小不变。
比的基本的性质:
2:3=(2×2):(3×2)=4:6
比的前项和后项同时乘以(或除以)一个
相同的数(0除外),比值不变。
利用商不变性质,我们可以进行除法的简算。
根据分数的基本性质,我们可以把分数化成最简分数。
4︰6
=
2︰3
前项、后项同时除以2
应用比的基本性质,我们可以把比化成最简单的整数比。
2
3
前、后项必须是整数,而且互质.
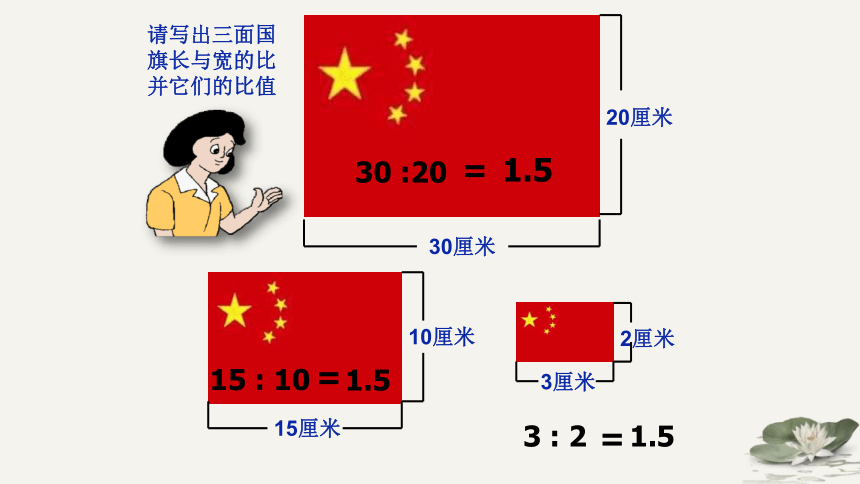
20厘米
30厘米
15厘米
10厘米
2厘米
3厘米
30
:20
=
1.5
15
:
10
=
1.5
3
:
2
=
1.5
请写出三面国旗长与宽的比并它们的比值
30
:
20
15
:
10
3
:
2
=
=
=
1.5
1.5
1.5
比值相等
30
:
20
=
15
:
10
=
3
:
2
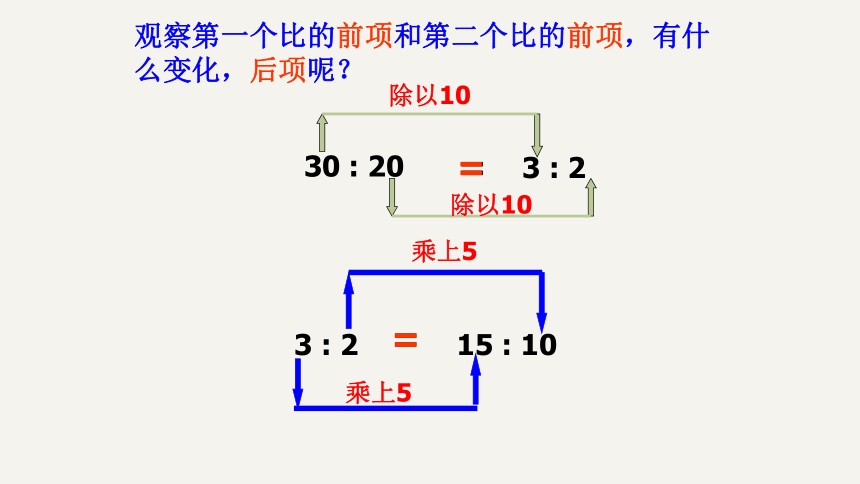
这三个比的比值有什么关系,这三个比呢?
30
:
20
3
:
2
除以10
除以10
乘上5
乘上5
=
观察第一个比的前项和第二个比的前项,有什么变化,后项呢?
=
15
:
10
3
:
2
=
=
比的前项和后项同时乘以或同时除以相同的数(
),比值不变。
比的基本性质:
a:b=(am):(bm)=(a÷m):(b÷m)
(b≠0,
m≠0
)
6:8
(6×0):(8×0)
≠
0除外
小蜗牛找家
5︰25
0.1︰0.4
20︰60
10︰8
︰1
5
1
2︰8
5:4
10:30
1:4
1:5
2:3
比的基本的性质
2:3=(2×2):(3×2)=4:6
比的前项和后项同时乘以(或除以)一个相同的数(0除外),比值不变。
30:20
15
:
10
3
:
2
国旗制法说明
:
1949年9月28日中国人民政治协商会议第一届全体会议主席团公布:
旗面为红色,长方形,其长与宽为三与二之比,旗面左上方缀黄色五角星五颗。一星较大,其外接圆直径为旗宽十分之三,居左;四星较小,其外接圆直径为旗高十分之一,环拱于大星之右。旗杆套为白色。
=
(
)
︰
6
1
9
2
×
18
(
)
×
18
=
3︰4
︰
6
1
9
2
同时乘6和9的最小公倍数
(2)把下面各比化成最简单的整数比。
︰
6
1
9
2
0.75︰2
例1
把下面各比化成最简整数比。
6
4
(1)12
?
18
(2)
5
?
3
(3)1.8
?0.09
解:12
?18
整数比
最简化
=(12÷6)
?(18÷6)前项和后项同时除以最大公约数6
解:1.8
?
0.09
小数比
整数比
=(1.8×100)
?(0.09×100)
比的前项和后项同时乘
以相同的数100
=
2
?
3
=(
)?(
)整数比
最简化
180
9
=(
)?(
)
20
1
4
4
5
6
?
3
=
(
5
6
?
(
3
×12)
×12)
=10
?
9
比的基本的性质
2:3=(2×2):(3×2)=4:6
比的前项和后项同时乘以(或除以)一个相同的数(0除外),比值不变。
分数比
整数比
比的前项和后项同时乘
以它们的分母的最小公倍数
(2)把下面各比化成最简单的整数比。
︰
6
1
9
2
0.75︰2
0.75︰2
=(0.75×100)︰(2×100)
=75︰200
=3︰8
不管哪种方法,最后的结果应该是一个最简的整数比,而不是一个数。
长:0.65米
宽:4分米
例2:求图中消防橱窗的长与宽的比。
解:0.65米:4分米
=6.5分米:4分米
=(6.5
×10):(
4
×10)
=40:65
=8:13
写出各杯子中糖与水的质量比。
这几杯糖水有一样甜的吗?
他们的说法对吗?
0.4∶1化简后是
。
0.48∶0.6化简后是0.8。
2
5
1
2
1
化简后是
。
3
4
︰
1
2
×
√
×
你听说过“黄金比”吗?黄金比的比值约等于0.618。从古希腊以来,一直有人认为把黄金比应用于造型艺术,可以使作品给人以最美的感觉。因此,黄金比在日常生活中有着广泛的应用。
你知道吗?
这节课你学到了那些知识?有什么收获?
单位统一是前提,
化整之后再化简;
直到前后项互素,
才是最简整数比。
生产一批零件,甲单独做6小时完成,乙单
独做8小时完成.
(1)甲完成任务的时间与乙完成任务的时间的
最简整数比是
(2)甲的工作效率与乙的工作效率的最简整数比是
(3)乙的工作效率与甲的工作效率的最简整数比是
智力大冲浪
拓展练习
3.2
比
的
基
本
性
质
13÷18=
(
)
(
)
=
(
):
(
)
除法
分数
比
13
18
13
18
前项
:(比号)
后项
比值
分子
_____
(分数线)
分母
分数值
被除数
÷(除号)
除数
商
记忆宝库
在括号里填上适当的数,
使等式成立
80÷10=800÷(
)=(
)÷5
100
40
3
4
=
(
)
16
=
6
(
)
12
8
填空:
你还记得除法中有什么性质?分数中又有什么性质吗?
商不变的性质:
分数的基本性质:
2÷3=(2×2)÷(3×2)=4÷6
3
2
2×2
3×2
6
4
=
=
在除法里,被除数和除数同时乘以(或除以)
一个相同的数(0除外),商不变。
分数的分子和分母同时乘以(或除以)一个
相同的数(0除外),分数的大小不变。
比的基本的性质:
2:3=(2×2):(3×2)=4:6
比的前项和后项同时乘以(或除以)一个
相同的数(0除外),比值不变。
利用商不变性质,我们可以进行除法的简算。
根据分数的基本性质,我们可以把分数化成最简分数。
4︰6
=
2︰3
前项、后项同时除以2
应用比的基本性质,我们可以把比化成最简单的整数比。
2
3
前、后项必须是整数,而且互质.
20厘米
30厘米
15厘米
10厘米
2厘米
3厘米
30
:20
=
1.5
15
:
10
=
1.5
3
:
2
=
1.5
请写出三面国旗长与宽的比并它们的比值
30
:
20
15
:
10
3
:
2
=
=
=
1.5
1.5
1.5
比值相等
30
:
20
=
15
:
10
=
3
:
2
这三个比的比值有什么关系,这三个比呢?
30
:
20
3
:
2
除以10
除以10
乘上5
乘上5
=
观察第一个比的前项和第二个比的前项,有什么变化,后项呢?
=
15
:
10
3
:
2
=
=
比的前项和后项同时乘以或同时除以相同的数(
),比值不变。
比的基本性质:
a:b=(am):(bm)=(a÷m):(b÷m)
(b≠0,
m≠0
)
6:8
(6×0):(8×0)
≠
0除外
小蜗牛找家
5︰25
0.1︰0.4
20︰60
10︰8
︰1
5
1
2︰8
5:4
10:30
1:4
1:5
2:3
比的基本的性质
2:3=(2×2):(3×2)=4:6
比的前项和后项同时乘以(或除以)一个相同的数(0除外),比值不变。
30:20
15
:
10
3
:
2
国旗制法说明
:
1949年9月28日中国人民政治协商会议第一届全体会议主席团公布:
旗面为红色,长方形,其长与宽为三与二之比,旗面左上方缀黄色五角星五颗。一星较大,其外接圆直径为旗宽十分之三,居左;四星较小,其外接圆直径为旗高十分之一,环拱于大星之右。旗杆套为白色。
=
(
)
︰
6
1
9
2
×
18
(
)
×
18
=
3︰4
︰
6
1
9
2
同时乘6和9的最小公倍数
(2)把下面各比化成最简单的整数比。
︰
6
1
9
2
0.75︰2
例1
把下面各比化成最简整数比。
6
4
(1)12
?
18
(2)
5
?
3
(3)1.8
?0.09
解:12
?18
整数比
最简化
=(12÷6)
?(18÷6)前项和后项同时除以最大公约数6
解:1.8
?
0.09
小数比
整数比
=(1.8×100)
?(0.09×100)
比的前项和后项同时乘
以相同的数100
=
2
?
3
=(
)?(
)整数比
最简化
180
9
=(
)?(
)
20
1
4
4
5
6
?
3
=
(
5
6
?
(
3
×12)
×12)
=10
?
9
比的基本的性质
2:3=(2×2):(3×2)=4:6
比的前项和后项同时乘以(或除以)一个相同的数(0除外),比值不变。
分数比
整数比
比的前项和后项同时乘
以它们的分母的最小公倍数
(2)把下面各比化成最简单的整数比。
︰
6
1
9
2
0.75︰2
0.75︰2
=(0.75×100)︰(2×100)
=75︰200
=3︰8
不管哪种方法,最后的结果应该是一个最简的整数比,而不是一个数。
长:0.65米
宽:4分米
例2:求图中消防橱窗的长与宽的比。
解:0.65米:4分米
=6.5分米:4分米
=(6.5
×10):(
4
×10)
=40:65
=8:13
写出各杯子中糖与水的质量比。
这几杯糖水有一样甜的吗?
他们的说法对吗?
0.4∶1化简后是
。
0.48∶0.6化简后是0.8。
2
5
1
2
1
化简后是
。
3
4
︰
1
2
×
√
×
你听说过“黄金比”吗?黄金比的比值约等于0.618。从古希腊以来,一直有人认为把黄金比应用于造型艺术,可以使作品给人以最美的感觉。因此,黄金比在日常生活中有着广泛的应用。
你知道吗?
这节课你学到了那些知识?有什么收获?
单位统一是前提,
化整之后再化简;
直到前后项互素,
才是最简整数比。
生产一批零件,甲单独做6小时完成,乙单
独做8小时完成.
(1)甲完成任务的时间与乙完成任务的时间的
最简整数比是
(2)甲的工作效率与乙的工作效率的最简整数比是
(3)乙的工作效率与甲的工作效率的最简整数比是
智力大冲浪
拓展练习
