6.4《生活中的圆周运动》教学设计—2021-2022学年高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 6.4《生活中的圆周运动》教学设计—2021-2022学年高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 273.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-23 16:30:06 | ||
图片预览


文档简介
6.4
生活中的圆周运动
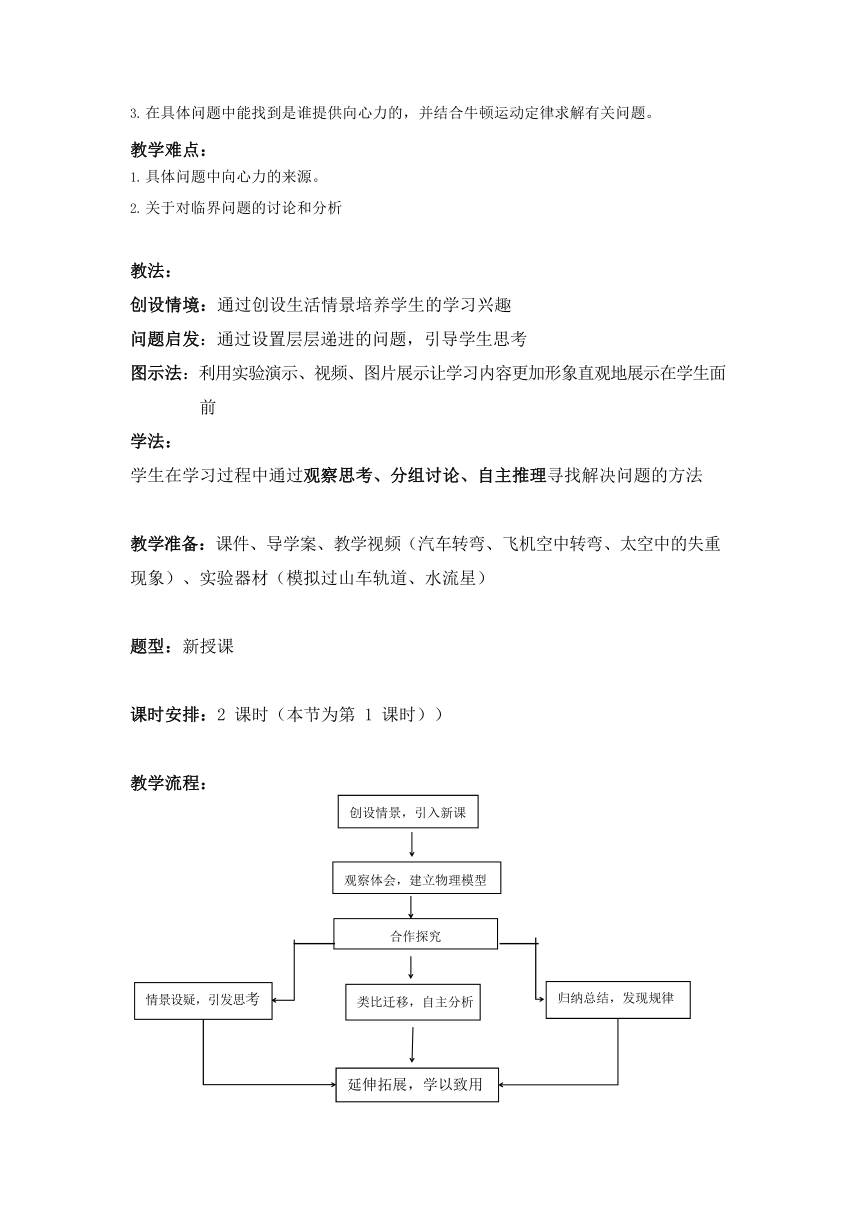
大单元教学分析:
(
第
一
章
运
动
的描述
第
二
章
匀
变
速直
线
运动
的
研
究
第
三
章
相
互
作
用
—
—力
第四
章运动和力的
关系
第五
章
抛体
运动
第六
章
圆周
运动
第七
章万有引力与宇宙
航
行
空间拓展
牛顿运动定律的应用
现象
本质
应用
运动与力的关系
)
(
非匀变速曲线运动
)
(
匀变速曲线运动
)
(
匀变速直线运动
)力与运动
(
生
活
中
的
圆
)
(
周
)
(
运
)
(
动
)
(
向
心
加
速
度
)
(
向
心
力
)
(
圆
周
运
动
)教材分析:
本节课是人教版必修
2
第六章的第四节,是对牛顿运动定律应用的升华,通过学生建立圆周运动的模型,研究圆周运动规律在生活中的具体应用,使学生深入理解圆周运动规律,
体会物理学在生活中的应用以及对社会发展的影响,本节教材中的事例很有代表性,与生活
联系紧密,学生易于观察,火车转弯、汽车过拱形桥的例子,既有水平面内的匀速圆周运动,
也有竖直平面内的非匀速圆周运动,并且进一步拓展,由地上的圆周运动延伸到“天上”的圆周运动,帮助学生感受到规律的统一,同时也为后续知识的学习(万有引力和宇宙航行、带粒子在匀强磁场中的圆周运动等)奠定基础。
学情分析:
通过前面的学习,学生已知道描述圆周运动的基本物理量(如线速度、角速度、向心加速度等和向心力)
,并且已经知道在一般的曲线运动中,曲线各部分曲率半径不一样,但在研究极短的一小段时,就可以看成是某个圆周运动的一部分,利用圆周运动的分析方法处理。
其次对向心力的理解还不够透彻,导致不能正确的分析向心力的来源以及运用牛顿运动定律列动力学方程。
高一阶段的学生,形象思维习惯较多,逻辑思维的能力有待提高,掌握部分的物理研究方法,但还需要进一步培养。
根据学生实际情况,本节内容安排两课时,第
1
课时只研究前两部分,铁路的弯道分析之前,先分析学生更为熟悉的汽车在水平路面转弯,这样做的目的是为了让学生的探究从易到难形成梯度。
教学目标:
物理观念:树立运动与相互作用观念,加深学生对向心力的认识,使其会在实际问题
中分析向心力的来源,并进行简单运算。
科学思维:通过对火车转弯、拱形桥看做匀速圆周运动的实例分析,渗透理论联系实
际的观点,提高学生分析和解决问题的能力。
科学探究:通过火车转弯、拱形桥物理模型的巩固,体会建立物理模型在物理学习中
的重要性。
科学态度与责任:(1)通过向心力在具体问题中的应用,培养学生将物理知识应用
于生活和生产实践的意识
(2)通过圆周运动在生活中的应用,加强学生的安全意识,强化学生的社会责任感
教学重点:
理解向心力是一种效果力。
准确描述物体的运动(定轨道、圆心、半径)
在具体问题中能找到是谁提供向心力的,并结合牛顿运动定律求解有关问题。
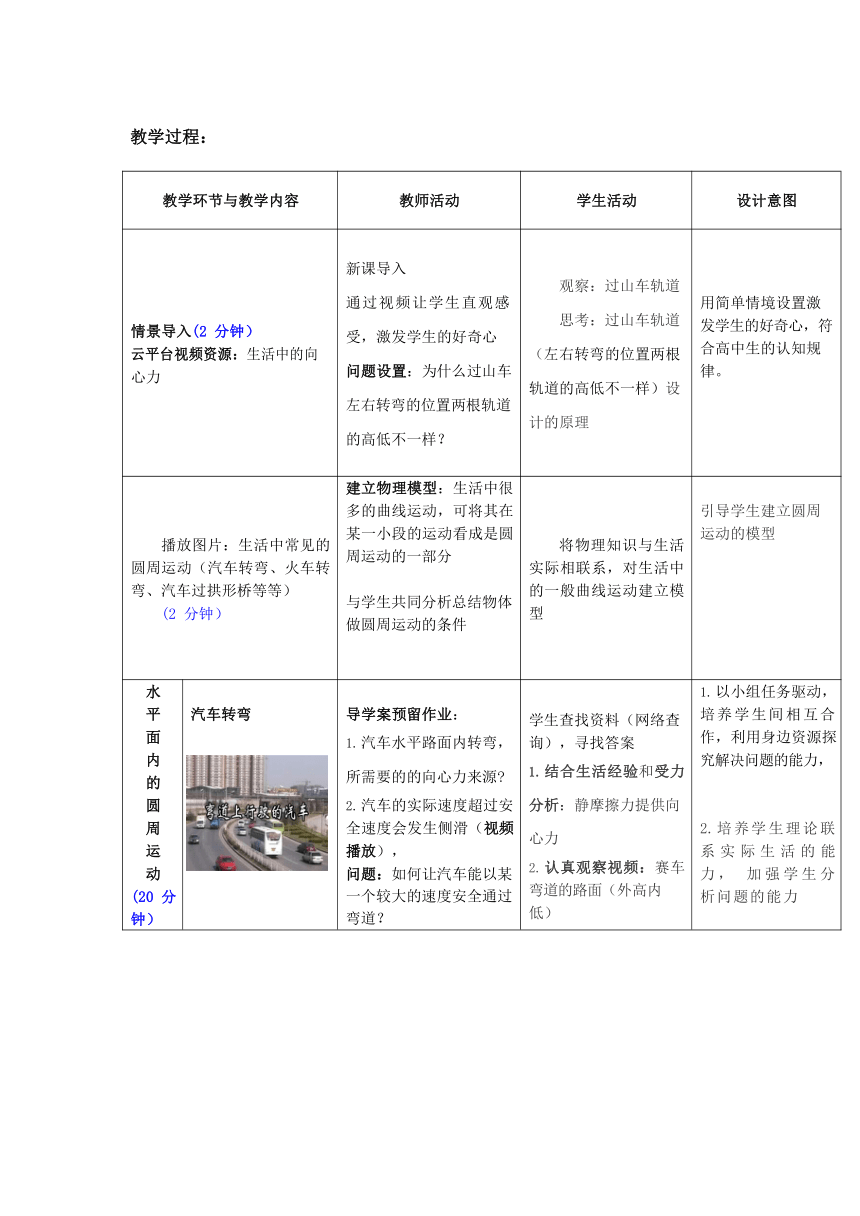
教学难点:
具体问题中向心力的来源。
关于对临界问题的讨论和分析
教法:
创设情境:通过创设生活情景培养学生的学习兴趣
问题启发:通过设置层层递进的问题,引导学生思考
图示法:利用实验演示、视频、图片展示让学习内容更加形象直观地展示在学生面前
学法:
学生在学习过程中通过观察思考、分组讨论、自主推理寻找解决问题的方法
教学准备:课件、导学案、教学视频(汽车转弯、飞机空中转弯、太空中的失重现象)、实验器材(模拟过山车轨道、水流星)
题型:新授课
课时安排:2
课时(本节为第
1
课时))
教学流程:
创设情景,引入新课
(
类比迁移,自主分析
)观察体会,建立物理模型
(
合作探究
情景设疑,引发思
考
归纳总结,发现规律
延伸拓展,学以致用
)
教学过程:
教学环节与教学内容
教师活动
学生活动
设计意图
情景导入(2
分钟)
云平台视频资源:生活中的向心力
新课导入
通过视频让学生直观感受,激发学生的好奇心
问题设置:为什么过山车左右转弯的位置两根轨道的高低不一样?
观察:过山车轨道思考:过山车轨道
(左右转弯的位置两根轨道的高低不一样)设计的原理
用简单情境设置激发学生的好奇心,符合高中生的认知规律。
播放图片:生活中常见的圆周运动(汽车转弯、火车转弯、汽车过拱形桥等等)
(2
分钟)
建立物理模型:生活中很多的曲线运动,可将其在某一小段的运动看成是圆周运动的一部分
与学生共同分析总结物体做圆周运动的条件
将物理知识与生活实际相联系,对生活中的一般曲线运动建立模型
引导学生建立圆周运动的模型
水平面内的圆周运动
(20
分
钟)
汽车转弯
导学案预留作业:
汽车水平路面内转弯,
所需要的的向心力来源?
汽车的实际速度超过安全速度会发生侧滑(视频播放),
问题:如何让汽车能以某
一个较大的速度安全通过弯道?
学生查找资料(网络查询),寻找答案
结合生活经验和受力
分析:静摩擦力提供向心力
认真观察视频:赛车弯道的路面(外高内低)
以小组任务驱动,
培养学生间相互合作,利用身边资源探究解决问题的能力,
培养学生理论联系实际生活的能力,
加强学生分析问题的能力
火车转弯
内外轨道没有高度差
内外轨有高度差
建立模型:将火车一小段
(理解:将火车转弯看成是圆周运动模型)
1.观察火车车轮模型,
对轮缘有直观的认识
2.受力分析:内外轨道没有高度差的情况下,
外侧铁轨和外轮轮缘之间挤压产生的弹力提供向心力
阅读教材(类比汽车转弯):垫高外侧轨道
受力分析并引导学生计算,交流讨论得出结论(平板上传结果)
v2
Mgtanθ=M
R
v=
gRtanθ
时间内的运动看成是圆周
运动的一部分
1.
利用层层递进的
1.展示火车车轮模型
问题设置,激发学生
问题设置
的思维能力和逻辑
2.内外轨道没有高度差的
推理能力,培养学生
情况下,火车转弯的向心
计算能力
力来源
3.若长期挤压内轨与外轨
2.加强学生的安全
谁会先损坏?如何解决这
意识,强化学生的社
个问题?
4.内外轨有高度差,火车
会责任感
转弯的临界速度是多少?
5.如果实际速度不等于临
界速度,会出现怎样的问
题?
引导学生利用类比
知识拓展:飞机在空
中盘旋(
类比迁移)
播放视频:飞机在空中转弯,引导学生认真观察,
受力分析,建立模型
分析向心力来源,并归纳总结解决相关问题的思想和方法
的方法分析解决问题
竖直面内的圆周
以任务形式引导学
导学案预留作业:
查找资料:生活中的桥梁
问题设置:生活中的桥梁是凸形桥多一些还是凹形桥多一些?这样设计的原因?
学生课前查阅桥梁相关资料
生在生活中仔细观察,并将生活与物理知识相联系
运动
(17
分钟)
情景引入:质量为
m
的汽车在拱形桥上以速度
v
行驶,探究向心力的来源
问题设置:
汽车过拱形桥是什么运动?
(在最高点)所需向心力的来源?
汽车对桥面的压力随汽车速度如何变化?
汽车速度过快会怎样,
有没有可能对桥面的压力为零?
通过运动分析、受力分析:汽车通过最高点附近可看成圆周运动,重力和支持力的合力提供向心力,并列牛顿定律表达式进行分析
通过理论分析联系生活实际,培养学生分析问题的能力
强化安全行驶的意识
思维拓展:航天器中的失重现象
问题设置:
如果将地球看做一个巨大的拱形桥,桥面半径就是地球半径。速度大到一定程度时,地面对车的支持力是零从而脱离地球?
播放视频:太空中的奇景
交流讨论航天其中的宇航员的失重情况
激发学生的兴趣,引导学生利用类比的方法解决问题,培养学生的计算能力,并为下一章做铺垫
凹形桥
通过问题引导学生自行分析
一位同学在黑板上受力分析并板演过程
提升学生自我分析问题的能力
总结汽车过凹形桥情况
课后思考(2
分钟)
(实验演示)
过山车模型(最高点)
水流星模型(最高点)
培养学生自主学习的能力,节约课堂教学时间,提高教学效率
课堂小结(2
分钟)
知识层面:介绍了生活中汽车转弯、火车转弯、汽车过拱形桥的事例,
深入理解如何运动圆周运动和牛顿运动定律解决生活中的问题
通过本节课的学习,要深刻认识到建立物理模型对物理学习的重要性3.希望同学们在生活中要多多观察,多多思考,将学习的物理知识应用到生活中
课后作业
见文件“课后作业”
板书设计
6.4
生活中的圆周运动
火车转弯
mgtanθ=mv2/R
V=
gR
tan
(临界速度)
汽车过拱形桥
凸形桥:mg-FN=mv
/R
FN=0,V=
gR
(完全失重)
2
2
凹形桥:FN-mg=mv
/R
教学反思
自我评价:
本节课是圆周运动的综合应用课,选择的实例比较贴近生活,但是学生对此并没有深入了解,对生活中的圆周运动的理性认识较少。因此在本节课的课堂教学中,我主要通过层层设疑,配合视频播放,调动学生的兴趣,
引导学生积极思考问题,并且通过导学案发布预习任务,以任务形式驱动学生积极主动去探究,同时引导学生归纳总结解决问题的思路和方法,利用类比迁移,
解决相关的问题,
培养学生举一反三的能力,
在整个教学过程中凸显学生的主体地位,
问题反思与教学重建
学生对汽车(火车)在倾斜路面上做圆周运动的轨道难以确认,较多的同学认为轨道平面沿斜面方向——(引入类似模型“倒圆锥”帮助学生理解)
在教学过程中,借助实物模型帮助学生理解问题,但这种教学手段只能帮助学生进行定性分析,对定量理解还有所欠缺——(在条件允许的情况下可利用力学传感器进一步进行定量探究)
本节内容理论知识的设计较多,学生理解不够透彻——(在教材难点的地方还需要适当地放缓节奏,给予学生更多的时间进行思考和讨论,
并配合相关的习题帮助学生巩固所学知识)
课堂教学时间有限,部分拓展知识可留作课后思考,既节约课堂时间,也培养学生自主分析解决问题的能力
生活中的圆周运动
大单元教学分析:
(
第
一
章
运
动
的描述
第
二
章
匀
变
速直
线
运动
的
研
究
第
三
章
相
互
作
用
—
—力
第四
章运动和力的
关系
第五
章
抛体
运动
第六
章
圆周
运动
第七
章万有引力与宇宙
航
行
空间拓展
牛顿运动定律的应用
现象
本质
应用
运动与力的关系
)
(
非匀变速曲线运动
)
(
匀变速曲线运动
)
(
匀变速直线运动
)力与运动
(
生
活
中
的
圆
)
(
周
)
(
运
)
(
动
)
(
向
心
加
速
度
)
(
向
心
力
)
(
圆
周
运
动
)教材分析:
本节课是人教版必修
2
第六章的第四节,是对牛顿运动定律应用的升华,通过学生建立圆周运动的模型,研究圆周运动规律在生活中的具体应用,使学生深入理解圆周运动规律,
体会物理学在生活中的应用以及对社会发展的影响,本节教材中的事例很有代表性,与生活
联系紧密,学生易于观察,火车转弯、汽车过拱形桥的例子,既有水平面内的匀速圆周运动,
也有竖直平面内的非匀速圆周运动,并且进一步拓展,由地上的圆周运动延伸到“天上”的圆周运动,帮助学生感受到规律的统一,同时也为后续知识的学习(万有引力和宇宙航行、带粒子在匀强磁场中的圆周运动等)奠定基础。
学情分析:
通过前面的学习,学生已知道描述圆周运动的基本物理量(如线速度、角速度、向心加速度等和向心力)
,并且已经知道在一般的曲线运动中,曲线各部分曲率半径不一样,但在研究极短的一小段时,就可以看成是某个圆周运动的一部分,利用圆周运动的分析方法处理。
其次对向心力的理解还不够透彻,导致不能正确的分析向心力的来源以及运用牛顿运动定律列动力学方程。
高一阶段的学生,形象思维习惯较多,逻辑思维的能力有待提高,掌握部分的物理研究方法,但还需要进一步培养。
根据学生实际情况,本节内容安排两课时,第
1
课时只研究前两部分,铁路的弯道分析之前,先分析学生更为熟悉的汽车在水平路面转弯,这样做的目的是为了让学生的探究从易到难形成梯度。
教学目标:
物理观念:树立运动与相互作用观念,加深学生对向心力的认识,使其会在实际问题
中分析向心力的来源,并进行简单运算。
科学思维:通过对火车转弯、拱形桥看做匀速圆周运动的实例分析,渗透理论联系实
际的观点,提高学生分析和解决问题的能力。
科学探究:通过火车转弯、拱形桥物理模型的巩固,体会建立物理模型在物理学习中
的重要性。
科学态度与责任:(1)通过向心力在具体问题中的应用,培养学生将物理知识应用
于生活和生产实践的意识
(2)通过圆周运动在生活中的应用,加强学生的安全意识,强化学生的社会责任感
教学重点:
理解向心力是一种效果力。
准确描述物体的运动(定轨道、圆心、半径)
在具体问题中能找到是谁提供向心力的,并结合牛顿运动定律求解有关问题。
教学难点:
具体问题中向心力的来源。
关于对临界问题的讨论和分析
教法:
创设情境:通过创设生活情景培养学生的学习兴趣
问题启发:通过设置层层递进的问题,引导学生思考
图示法:利用实验演示、视频、图片展示让学习内容更加形象直观地展示在学生面前
学法:
学生在学习过程中通过观察思考、分组讨论、自主推理寻找解决问题的方法
教学准备:课件、导学案、教学视频(汽车转弯、飞机空中转弯、太空中的失重现象)、实验器材(模拟过山车轨道、水流星)
题型:新授课
课时安排:2
课时(本节为第
1
课时))
教学流程:
创设情景,引入新课
(
类比迁移,自主分析
)观察体会,建立物理模型
(
合作探究
情景设疑,引发思
考
归纳总结,发现规律
延伸拓展,学以致用
)
教学过程:
教学环节与教学内容
教师活动
学生活动
设计意图
情景导入(2
分钟)
云平台视频资源:生活中的向心力
新课导入
通过视频让学生直观感受,激发学生的好奇心
问题设置:为什么过山车左右转弯的位置两根轨道的高低不一样?
观察:过山车轨道思考:过山车轨道
(左右转弯的位置两根轨道的高低不一样)设计的原理
用简单情境设置激发学生的好奇心,符合高中生的认知规律。
播放图片:生活中常见的圆周运动(汽车转弯、火车转弯、汽车过拱形桥等等)
(2
分钟)
建立物理模型:生活中很多的曲线运动,可将其在某一小段的运动看成是圆周运动的一部分
与学生共同分析总结物体做圆周运动的条件
将物理知识与生活实际相联系,对生活中的一般曲线运动建立模型
引导学生建立圆周运动的模型
水平面内的圆周运动
(20
分
钟)
汽车转弯
导学案预留作业:
汽车水平路面内转弯,
所需要的的向心力来源?
汽车的实际速度超过安全速度会发生侧滑(视频播放),
问题:如何让汽车能以某
一个较大的速度安全通过弯道?
学生查找资料(网络查询),寻找答案
结合生活经验和受力
分析:静摩擦力提供向心力
认真观察视频:赛车弯道的路面(外高内低)
以小组任务驱动,
培养学生间相互合作,利用身边资源探究解决问题的能力,
培养学生理论联系实际生活的能力,
加强学生分析问题的能力
火车转弯
内外轨道没有高度差
内外轨有高度差
建立模型:将火车一小段
(理解:将火车转弯看成是圆周运动模型)
1.观察火车车轮模型,
对轮缘有直观的认识
2.受力分析:内外轨道没有高度差的情况下,
外侧铁轨和外轮轮缘之间挤压产生的弹力提供向心力
阅读教材(类比汽车转弯):垫高外侧轨道
受力分析并引导学生计算,交流讨论得出结论(平板上传结果)
v2
Mgtanθ=M
R
v=
gRtanθ
时间内的运动看成是圆周
运动的一部分
1.
利用层层递进的
1.展示火车车轮模型
问题设置,激发学生
问题设置
的思维能力和逻辑
2.内外轨道没有高度差的
推理能力,培养学生
情况下,火车转弯的向心
计算能力
力来源
3.若长期挤压内轨与外轨
2.加强学生的安全
谁会先损坏?如何解决这
意识,强化学生的社
个问题?
4.内外轨有高度差,火车
会责任感
转弯的临界速度是多少?
5.如果实际速度不等于临
界速度,会出现怎样的问
题?
引导学生利用类比
知识拓展:飞机在空
中盘旋(
类比迁移)
播放视频:飞机在空中转弯,引导学生认真观察,
受力分析,建立模型
分析向心力来源,并归纳总结解决相关问题的思想和方法
的方法分析解决问题
竖直面内的圆周
以任务形式引导学
导学案预留作业:
查找资料:生活中的桥梁
问题设置:生活中的桥梁是凸形桥多一些还是凹形桥多一些?这样设计的原因?
学生课前查阅桥梁相关资料
生在生活中仔细观察,并将生活与物理知识相联系
运动
(17
分钟)
情景引入:质量为
m
的汽车在拱形桥上以速度
v
行驶,探究向心力的来源
问题设置:
汽车过拱形桥是什么运动?
(在最高点)所需向心力的来源?
汽车对桥面的压力随汽车速度如何变化?
汽车速度过快会怎样,
有没有可能对桥面的压力为零?
通过运动分析、受力分析:汽车通过最高点附近可看成圆周运动,重力和支持力的合力提供向心力,并列牛顿定律表达式进行分析
通过理论分析联系生活实际,培养学生分析问题的能力
强化安全行驶的意识
思维拓展:航天器中的失重现象
问题设置:
如果将地球看做一个巨大的拱形桥,桥面半径就是地球半径。速度大到一定程度时,地面对车的支持力是零从而脱离地球?
播放视频:太空中的奇景
交流讨论航天其中的宇航员的失重情况
激发学生的兴趣,引导学生利用类比的方法解决问题,培养学生的计算能力,并为下一章做铺垫
凹形桥
通过问题引导学生自行分析
一位同学在黑板上受力分析并板演过程
提升学生自我分析问题的能力
总结汽车过凹形桥情况
课后思考(2
分钟)
(实验演示)
过山车模型(最高点)
水流星模型(最高点)
培养学生自主学习的能力,节约课堂教学时间,提高教学效率
课堂小结(2
分钟)
知识层面:介绍了生活中汽车转弯、火车转弯、汽车过拱形桥的事例,
深入理解如何运动圆周运动和牛顿运动定律解决生活中的问题
通过本节课的学习,要深刻认识到建立物理模型对物理学习的重要性3.希望同学们在生活中要多多观察,多多思考,将学习的物理知识应用到生活中
课后作业
见文件“课后作业”
板书设计
6.4
生活中的圆周运动
火车转弯
mgtanθ=mv2/R
V=
gR
tan
(临界速度)
汽车过拱形桥
凸形桥:mg-FN=mv
/R
FN=0,V=
gR
(完全失重)
2
2
凹形桥:FN-mg=mv
/R
教学反思
自我评价:
本节课是圆周运动的综合应用课,选择的实例比较贴近生活,但是学生对此并没有深入了解,对生活中的圆周运动的理性认识较少。因此在本节课的课堂教学中,我主要通过层层设疑,配合视频播放,调动学生的兴趣,
引导学生积极思考问题,并且通过导学案发布预习任务,以任务形式驱动学生积极主动去探究,同时引导学生归纳总结解决问题的思路和方法,利用类比迁移,
解决相关的问题,
培养学生举一反三的能力,
在整个教学过程中凸显学生的主体地位,
问题反思与教学重建
学生对汽车(火车)在倾斜路面上做圆周运动的轨道难以确认,较多的同学认为轨道平面沿斜面方向——(引入类似模型“倒圆锥”帮助学生理解)
在教学过程中,借助实物模型帮助学生理解问题,但这种教学手段只能帮助学生进行定性分析,对定量理解还有所欠缺——(在条件允许的情况下可利用力学传感器进一步进行定量探究)
本节内容理论知识的设计较多,学生理解不够透彻——(在教材难点的地方还需要适当地放缓节奏,给予学生更多的时间进行思考和讨论,
并配合相关的习题帮助学生巩固所学知识)
课堂教学时间有限,部分拓展知识可留作课后思考,既节约课堂时间,也培养学生自主分析解决问题的能力
