黑龙江省大庆市龙凤区(五四学制)2018-2019学年七年级上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省大庆市龙凤区(五四学制)2018-2019学年七年级上学期期末考试数学试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 266.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 23:02:57 | ||
图片预览



文档简介
2018—2019学年度上学期期末考试初二年级
数学试题
姓名:__________
班级:__________
考试注意:
1.
考生选在答题卡上作答,需将自己的姓名、考号填写到答题卡规定的位置。
2.
考试时间120分钟,试卷满分120分。
一、选择题(本大题共10小题,共30.0分)
1.
我国主要银行的商标设计基本上都融入了中国古代钱币的图案,如图是我国四个银行的商标图案,其中是轴对称图形的有( )
A.
①②③
B.
①②④
C.
①③④
D.
②③④
2.
小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )
A.
B.
C.
D.
3.
已知,如图,B、C、E三点在同一条直线上,AC=CD,
∠B=∠E=90°,
AB=CE,则不正确的结论是( )
A.
∠A与∠D互为余角
B.
∠A=∠2
C.
△ABC△CED
D.
∠1=∠2
4.
已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同。若随机从中摸出一个,
摸到红球的概率是,则袋中球的总个数是( )
A.
2
B.
4
C.
6
D.
8
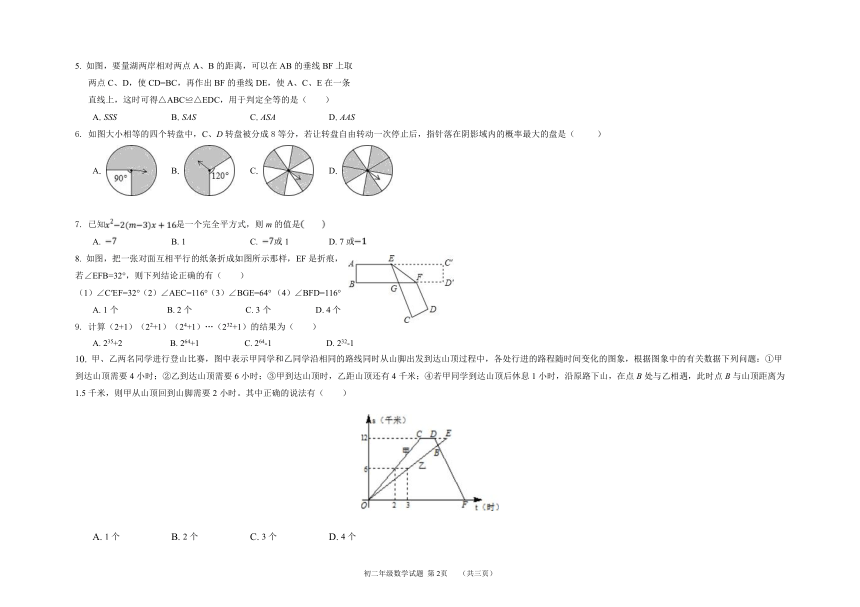
5.
如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取
两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条
直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.
SSS
B.
SAS
C.
ASA
D.
AAS
6.
如图大小相等的四个转盘中,C、D转盘被分成8等分,若让转盘自由转动一次停止后,指针落在阴影域内的概率最大的盘是(
)
A.
B.
C.
D.
7.
已知是一个完全平方式,则m的值是
A.
B.
1
C.
或1
D.
7或
8.
如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°?(4)∠BFD=116°
A.
1个
B.
2个
C.
3个
D.
4个
9.
计算(2+1)(22+1)(24+1)…(232+1)的结果为( )
A.
235+2
B.
264+1
C.
264-1
D.
232-1
10.
甲、乙两名同学进行登山比赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各处行进的路程随时间变化的图象,根据图象中的有关数据下列问题:①甲到达山顶需要4小时;②乙到达山顶需要6小时;③甲到达山顶时,乙距山顶还有4千米;④若甲同学到达山顶后休息1小时,沿原路下山,在点B处与乙相遇,此时点B与山顶距离为1.5千米,则甲从山顶回到山脚需要2小时。其中正确的说法有( )
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题(本大题共8小题,共24.0分)
11.
如图,已知,△ABC≌△BAE,∠ABE=60°,∠E=92°,则∠ABC的度数为______度。
12.
若a+b=,且ab=1,则(a+2)(b+2)=______。
13.
某水库的水位在6小时内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤6)的函数关系式为______。
14.
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=
______
15.
已知2x=3,2y=5,则22x+y-1=
______
。
16.
有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:
①线段;②正三角形;③平行四边形;④梯形;⑤圆。
将卡片背面朝上洗匀,从中任取一张,其正面图形是轴对称图形的概率是______。
17.已知2n+216+1是一个有理数的平方,则正整数n的值为
18.
如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点。点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动。若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为______
?厘米/秒。
三、计算题(本大题共4小题,共12.0分)
19.(1)(a2)3÷(-a)2;??????????
????
(2)(a+3b)2-(a-3b)2
(3)(-x6)-(-3x3)2+8[-(-x)3]2
(4)(-2)24(-0.125)8+20162-2015×2017.
四、解答题(本大题共7小题,共54.0分)
20.(6分)已知x2-x=5,求(2x+1)2-x(5+2x)+(2+x)(2-x)的值。
21.(6分)如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD的度数。
22.(7分)已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,
并说明理由。
23.
(10分)在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀。
(1)“从中任意抽取1个球不是红球就是白球”是______事件,“从中任意抽取1个球是黑球”是______事件;
(2)从中任意抽取1个球恰好是红球的概率是______;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙。你认为这个规则公平吗?请加以说明。
24.
(7分)已知(x2+mx+3)(nx2-3x+2)的展开式中不含x2项和x项,求m+n的值。
25.(10分)如图,表示甲、乙两同学沿同一条路到达目的地过程中,路程s(千米)与时间t(小时)之间关系的图象,根据图象中提供的信息回答问题:
(1)乙的速度为______千米/时;
(2)两人在乙出发后______小时相遇;
(3)点A处对应的数字为______;
(4)当t=2时,求甲乙之间的距离。
26.
(8分)已知直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处。
(1)若∠PEF=48°,点Q恰好落在其中的一条平行线上,请直接写出∠EFP的度数。
(2)若∠PEF=75°,∠CFQ=∠PFC,求∠EFP的度数。
2018—2019学年度上学期期末考试初二年级
数学参考答案及评分标准
1.
D
2.
D
3.
D
4.
D
5.
C
6.
A
7.
D
8.
D
9.
C
10.
D
11.
28
12.
12??
13.
y=8+0.2x??
14.
134°??
15.
??
16.
??
17.
30或9??
18.
4或6??
19.(12分)
解:(1)原式=a6÷a2=a4
(2)原式=(a+3b+a-3b)(a+3b-a+3b)=a?6b=4ab
(3)原式=-x6-9x6+8x6=-2x6;
(4)原式=[(-8)×(-0.125)]8+20162-(2016-1)×(2016+1)=1+20162-20162+1=2.??
20.
(6分)解:原式=4x2+4x+1-5x-2x2+4-x2=x2-x+5,
当x2-x=5时,原式=5+5=10.??
21.(6分)
解:∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥AB,
∴∠AGD=180°-∠BAC=180°-80°=100°.??
22.
(7分)解:OD=OC.
理由:连接AB.
在△ADB与△ACB中,
,
∴△ADB≌△ACB.
∴∠D=∠C,
在△ADO与△BCO中,
∵∠D=∠C,
∠DOA=∠COB(对顶角相等),
AD=BC,
∴△ADO≌△CBO,
∴OC=OD.??
23.(10分)
必然;不可能;??(3)此游戏不公平.如图所示:
,
由树状图可得:一共有20种可能,两球同色的有8种情况,故选择甲的概率为:=;
则选择乙的概率为:,
故此游戏不公平.
24.
(7)解:(x2+mx+3)(nx2-3x+2)
=nx4-3x3+2x2+mnx3-3mx2+2mx+3nx2-9x+6
=nx4+(-3+mn)x3+(2-3m+3n)x2+(2m-9)x+6,
∵(x2+mx+3)(nx2-3x+2)的展开式中不含x2项和x项,
∴2-3m+3n=0,2m-9=0,
解得:m=4.5,n=,
m+n=.??
25.(10)
12;0.8;9.6;3.5千米
26.(8)
解:(1)①如图1,当点Q落在AB上,
∴FP⊥AB,
∴∠EFP=90°-∠PEF=42°,
如图2,当点Q落在CD上,
∵将△EPF沿PF折叠,使顶点E落在点Q处,
∴PF垂直平分EQ,
∴∠1=∠2,
∵AB∥CD,
∴∠QFE=180°-∠PEF=132°,
∴∠PFE=QFE=66°;
(2)①如图3,当点Q在平行线AB,CD之间时,
设∠PFQ=x,由折叠可得∠EFP=x,
∵∠CFQ=PFC,
∴∠PFQ=∠CFQ=x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴75°+x+x+x=180°,
∴x=35°,
∴∠EFP=35°;
如图4,当点Q在CD的下方时,
设∠CFQ=x,由∠CFQ=PFC得,∠PFC=2x,
∴∠PFQ=3x,
由折叠得,∠PFE=∠PFQ=3x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2x+3x+75°=180°,
∴x=21°,
∠EFP=3x=63°,
综上所述,∠EFP的度数是35°或63°.??
班
级
姓
名
考
场
座位号
△△△△△
△△△△△
△△△△△
△△△△△○
△△△△△○
△△△△△
△△△△△冷
△△△△△静
△△△△△思
△△△△△考
△△△△△
△△△△△
△△△△△规
△△△△△范
△△△△△答
△△△△△题
△△△△△
△△△△△
△△△△△期
△△△△△待
△△△△△着
△△△△△你
△△△△△的
△△△△△进
△△△△△步
△△△△△
△△△△△
△△△△△○
△△△△△○
△△△△△
△△△△△
△△△△△
△△△△△
△△△△△
△△△△△
PAGE
初二年级数学试题
第1页
(共三页)
数学试题
姓名:__________
班级:__________
考试注意:
1.
考生选在答题卡上作答,需将自己的姓名、考号填写到答题卡规定的位置。
2.
考试时间120分钟,试卷满分120分。
一、选择题(本大题共10小题,共30.0分)
1.
我国主要银行的商标设计基本上都融入了中国古代钱币的图案,如图是我国四个银行的商标图案,其中是轴对称图形的有( )
A.
①②③
B.
①②④
C.
①③④
D.
②③④
2.
小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )
A.
B.
C.
D.
3.
已知,如图,B、C、E三点在同一条直线上,AC=CD,
∠B=∠E=90°,
AB=CE,则不正确的结论是( )
A.
∠A与∠D互为余角
B.
∠A=∠2
C.
△ABC△CED
D.
∠1=∠2
4.
已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同。若随机从中摸出一个,
摸到红球的概率是,则袋中球的总个数是( )
A.
2
B.
4
C.
6
D.
8
5.
如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取
两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条
直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.
SSS
B.
SAS
C.
ASA
D.
AAS
6.
如图大小相等的四个转盘中,C、D转盘被分成8等分,若让转盘自由转动一次停止后,指针落在阴影域内的概率最大的盘是(
)
A.
B.
C.
D.
7.
已知是一个完全平方式,则m的值是
A.
B.
1
C.
或1
D.
7或
8.
如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°?(4)∠BFD=116°
A.
1个
B.
2个
C.
3个
D.
4个
9.
计算(2+1)(22+1)(24+1)…(232+1)的结果为( )
A.
235+2
B.
264+1
C.
264-1
D.
232-1
10.
甲、乙两名同学进行登山比赛,图中表示甲同学和乙同学沿相同的路线同时从山脚出发到达山顶过程中,各处行进的路程随时间变化的图象,根据图象中的有关数据下列问题:①甲到达山顶需要4小时;②乙到达山顶需要6小时;③甲到达山顶时,乙距山顶还有4千米;④若甲同学到达山顶后休息1小时,沿原路下山,在点B处与乙相遇,此时点B与山顶距离为1.5千米,则甲从山顶回到山脚需要2小时。其中正确的说法有( )
A.
1个
B.
2个
C.
3个
D.
4个
二、填空题(本大题共8小题,共24.0分)
11.
如图,已知,△ABC≌△BAE,∠ABE=60°,∠E=92°,则∠ABC的度数为______度。
12.
若a+b=,且ab=1,则(a+2)(b+2)=______。
13.
某水库的水位在6小时内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤6)的函数关系式为______。
14.
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=
______
15.
已知2x=3,2y=5,则22x+y-1=
______
。
16.
有五张卡片(形状、大小、质地都相同),上面分别画有下列图形:
①线段;②正三角形;③平行四边形;④梯形;⑤圆。
将卡片背面朝上洗匀,从中任取一张,其正面图形是轴对称图形的概率是______。
17.已知2n+216+1是一个有理数的平方,则正整数n的值为
18.
如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点。点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动。若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为______
?厘米/秒。
三、计算题(本大题共4小题,共12.0分)
19.(1)(a2)3÷(-a)2;??????????
????
(2)(a+3b)2-(a-3b)2
(3)(-x6)-(-3x3)2+8[-(-x)3]2
(4)(-2)24(-0.125)8+20162-2015×2017.
四、解答题(本大题共7小题,共54.0分)
20.(6分)已知x2-x=5,求(2x+1)2-x(5+2x)+(2+x)(2-x)的值。
21.(6分)如图,EF∥AD,∠1=∠2,∠BAC=80°.求∠AGD的度数。
22.(7分)已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,
并说明理由。
23.
(10分)在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀。
(1)“从中任意抽取1个球不是红球就是白球”是______事件,“从中任意抽取1个球是黑球”是______事件;
(2)从中任意抽取1个球恰好是红球的概率是______;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙。你认为这个规则公平吗?请加以说明。
24.
(7分)已知(x2+mx+3)(nx2-3x+2)的展开式中不含x2项和x项,求m+n的值。
25.(10分)如图,表示甲、乙两同学沿同一条路到达目的地过程中,路程s(千米)与时间t(小时)之间关系的图象,根据图象中提供的信息回答问题:
(1)乙的速度为______千米/时;
(2)两人在乙出发后______小时相遇;
(3)点A处对应的数字为______;
(4)当t=2时,求甲乙之间的距离。
26.
(8分)已知直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处。
(1)若∠PEF=48°,点Q恰好落在其中的一条平行线上,请直接写出∠EFP的度数。
(2)若∠PEF=75°,∠CFQ=∠PFC,求∠EFP的度数。
2018—2019学年度上学期期末考试初二年级
数学参考答案及评分标准
1.
D
2.
D
3.
D
4.
D
5.
C
6.
A
7.
D
8.
D
9.
C
10.
D
11.
28
12.
12??
13.
y=8+0.2x??
14.
134°??
15.
??
16.
??
17.
30或9??
18.
4或6??
19.(12分)
解:(1)原式=a6÷a2=a4
(2)原式=(a+3b+a-3b)(a+3b-a+3b)=a?6b=4ab
(3)原式=-x6-9x6+8x6=-2x6;
(4)原式=[(-8)×(-0.125)]8+20162-(2016-1)×(2016+1)=1+20162-20162+1=2.??
20.
(6分)解:原式=4x2+4x+1-5x-2x2+4-x2=x2-x+5,
当x2-x=5时,原式=5+5=10.??
21.(6分)
解:∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥AB,
∴∠AGD=180°-∠BAC=180°-80°=100°.??
22.
(7分)解:OD=OC.
理由:连接AB.
在△ADB与△ACB中,
,
∴△ADB≌△ACB.
∴∠D=∠C,
在△ADO与△BCO中,
∵∠D=∠C,
∠DOA=∠COB(对顶角相等),
AD=BC,
∴△ADO≌△CBO,
∴OC=OD.??
23.(10分)
必然;不可能;??(3)此游戏不公平.如图所示:
,
由树状图可得:一共有20种可能,两球同色的有8种情况,故选择甲的概率为:=;
则选择乙的概率为:,
故此游戏不公平.
24.
(7)解:(x2+mx+3)(nx2-3x+2)
=nx4-3x3+2x2+mnx3-3mx2+2mx+3nx2-9x+6
=nx4+(-3+mn)x3+(2-3m+3n)x2+(2m-9)x+6,
∵(x2+mx+3)(nx2-3x+2)的展开式中不含x2项和x项,
∴2-3m+3n=0,2m-9=0,
解得:m=4.5,n=,
m+n=.??
25.(10)
12;0.8;9.6;3.5千米
26.(8)
解:(1)①如图1,当点Q落在AB上,
∴FP⊥AB,
∴∠EFP=90°-∠PEF=42°,
如图2,当点Q落在CD上,
∵将△EPF沿PF折叠,使顶点E落在点Q处,
∴PF垂直平分EQ,
∴∠1=∠2,
∵AB∥CD,
∴∠QFE=180°-∠PEF=132°,
∴∠PFE=QFE=66°;
(2)①如图3,当点Q在平行线AB,CD之间时,
设∠PFQ=x,由折叠可得∠EFP=x,
∵∠CFQ=PFC,
∴∠PFQ=∠CFQ=x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴75°+x+x+x=180°,
∴x=35°,
∴∠EFP=35°;
如图4,当点Q在CD的下方时,
设∠CFQ=x,由∠CFQ=PFC得,∠PFC=2x,
∴∠PFQ=3x,
由折叠得,∠PFE=∠PFQ=3x,
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∴2x+3x+75°=180°,
∴x=21°,
∠EFP=3x=63°,
综上所述,∠EFP的度数是35°或63°.??
班
级
姓
名
考
场
座位号
△△△△△
△△△△△
△△△△△
△△△△△○
△△△△△○
△△△△△
△△△△△冷
△△△△△静
△△△△△思
△△△△△考
△△△△△
△△△△△
△△△△△规
△△△△△范
△△△△△答
△△△△△题
△△△△△
△△△△△
△△△△△期
△△△△△待
△△△△△着
△△△△△你
△△△△△的
△△△△△进
△△△△△步
△△△△△
△△△△△
△△△△△○
△△△△△○
△△△△△
△△△△△
△△△△△
△△△△△
△△△△△
△△△△△
PAGE
初二年级数学试题
第1页
(共三页)
同课章节目录
