黑龙江省大庆市龙凤区(五四学制)2018-2019学年九年级上学期期末考试数学试卷(word版含答案)
文档属性
| 名称 | 黑龙江省大庆市龙凤区(五四学制)2018-2019学年九年级上学期期末考试数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 367.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 23:06:14 | ||
图片预览




文档简介
2018--2019学年度第一学期期未龙凤区
?????
?九年级???数学试卷
时间:120分钟
总分:120分
一、选择题(本大题共10小题,每小题3分,共30分)
1.
2cos30°=( )
A.1
B.
C.
D.
2.一种花粉颗粒直径约为0.0000085米,数字0.0000085用科学记数法表示为( )
A.0.85×10﹣5
B.85×10﹣7
C.8.5×10﹣6
D.8.5×10﹣5
3.已知两个有理数a,b,如果ab>0且a+b<0,那么( )
A.a>0,b>0
B.a<0,b<
0
C.a、b同号
D.a、b异号,且正数的绝对值较大
4.一个正n边形的每一个外角都是72°,则n=( )
A.5
B.6
C.7
D.8
5.某商品打七折后价格为a元,则原价为( )
A.a元
B.a元
C.30%a元
D.a元
6.如果两个相似三角形对应边之比是1:4,那么它们的对应中线之比是( )
A.1:2
B.1:4
C.1:8
D.1:16
7.一次函数与二次函数在同一坐标系内的图象可能是(
)
8.如图所示的工件的主视图是
(
)
9.从分别写有数字1,2,3,4,5的5张卡片中依次取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是3的倍数的概率是(
)
A
.
B.
C.
D
.
10..抛物线中,b=4a,它的图象如图,有以下结论:①;②
③
④
⑤
⑥;其中正确的为(
)
A.①②
B.①④
C.①②⑥
D.①③⑤
二、填空题(本大题共10小题,每小题3分,共30分)
11.分解因式
=
.
12.函数=自变量的取值范围是
.
13.在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为
.
14.已知2x=3,2y=5,则22x﹣y的值是
.
15.若关于x的不等式组
HYPERLINK
"http://www..cn"
EMBED
Equation.DSMT4
解集为x<2,则a的取值范围是??
.
16.
关于x的分式方程的解是负数,则m的取值范围为
.
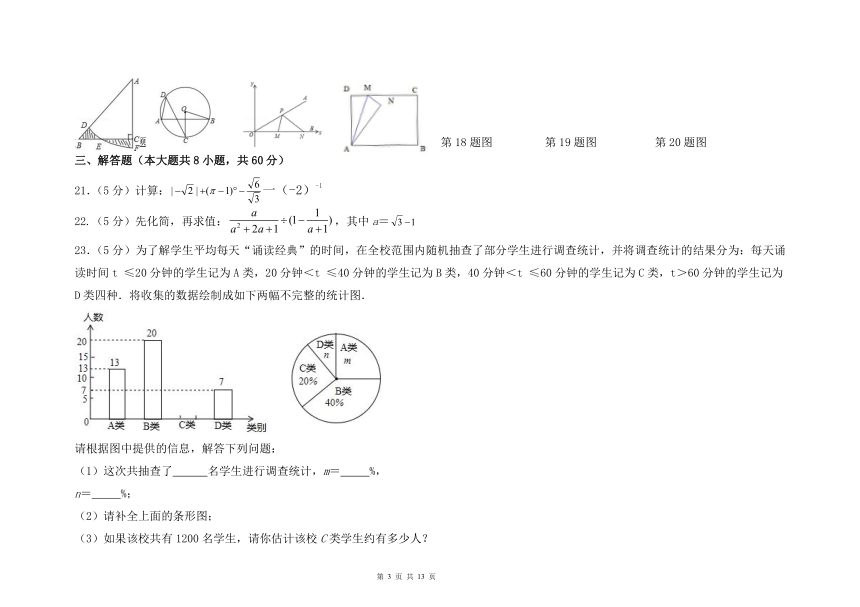
17.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 (结果保留根号).
18.如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=______度.
19.如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为______.
20.
如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM?,连接BN,当DM=1时,则△ABN的面积是
。
第17题
第18题图
第19题图
第20题图
三、解答题(本大题共8小题,共60分)
21.(5分)计算:一(-2)-1
22.(5分)先化简,再求值:,其中a=
23.(5分)为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t
≤20分钟的学生记为A类,20分钟<t
≤40分钟的学生记为B类,40分钟<t
≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)这次共抽查了
名学生进行调查统计,m=
%,
n=
%;
(2)请补全上面的条形图;
(3)如果该校共有1200名学生,请你估计该校C类学生约有多少人?
24.(9分)AB是⊙O的直径,弦DF⊥AB于E,连接BD.点C在BA的延长线上,且∠CDE=2∠B.连接CD,CD=8,AC=4.
(1)CD是⊙O的切线吗?请说明理由;
(2)求DF的长;
(3)求tan∠B.
25.
(9分)某公司经营甲、乙两种商品,每件甲种商品进价12万元,售价14.5万元.每件乙种商品进价8万元,售价10万元,且它们的进价和售价始终不变.现准备购进甲、乙两种商品共20件,所用资金不低于190万元不高于200万元.
(1)该公司有哪几种进货方案?
(2)该公司采用哪种进货方案可获得最大利润?最大利润是多少?
(3)利用(2)中所求得的最大利润再次进货,请直接写出获得最大利润的进货方案
26.(9分)在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
(1)求圆形区域的面积;
(2)某时刻海面上出现-渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离.(≈1.7,保留三个有效数字);
(3)当渔船A由(2)中位置向正西方向航行时,是否会进入海洋生物保护区?通过计算回答。
27.(9分)如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由.
(2)请给出一个能反映AB、AC和FA的数量关系的一个等式,并说明你给出的等式成立.
28.(9分)
抛物线平移后的位置如图所示,点、坐标分别为(,0),(3,0),设平移后的抛物线与轴交于点,其顶点为。
(1)求平移后的抛物线的对称轴、解析式和点的坐标;
(2)和是否相等?请证明你的结论。
(3)点在平移后的抛物线的对称轴上,
且与相似,求点的坐标。
2018--2019学年度第一学期期未龙凤区答案
?????
?九年级???数学试卷
总分:120分
一.选择题:(共10题,每题3分,共30分)
1.B
2.
C
3.B
4.A
5.B
6.B
7.B
8.A
9.C
10.C
二.填空题:(共10题,每题3分,共30分)
11.a(1+a)(1-a)
12.x>1/2
13.2
14.9/5
15.a≥2
16.m>-8且m≠-4
17.
2
√Π/Π
18.
35
19.(
3/2
,√3/2)
20.
24/5
三.解答题(8道题,共60分)
21.(5分)解:原式=√2+1-
√2
+1/2
..............3分
=3/2
................5分
22.(5分)先化简,再求值。
解:原式=1/a+1
..............3分
结果等于√3/3
.............5分
23.
(5分)(1)50,
26,
14
.......共3分(每空1分)
(2)C类:50X20%=10人,补长方图略。.......1分
(3)1200X20%=240
........1分
24.
(本题9分,每问3分)
解:(1)连接DO.
∵OD=OB∴∠DBC=∠ODB
∴∠DOC=2∠DBO
………1分
∵∠CDE=2∠DBO
∴∠CDE=∠DOC
………2分
∴∠EDO+∠DOE=∠EDO
+∠CDE=
即∠CDO=
∴OD⊥CD
∴CD是⊙O切线
…………3分
(2)设⊙O的半径为R
在Rt△ODC中,
∠CDO=,
由勾股定理可知
即
∴R=6
………1分
∴OC=10
由面积公式可知
∴DE=
………2分
∵AB⊥DF,AB为⊙O直径
∴DF
=2DE=
…………3分
(3)由勾股定理求出OE=18/5
………1分
BE=48/5
………2分
在
Rt△DEB中,
tanB=DE/BE
=3/4
………3分
25.
(本题9分,每问3分。)
(1)设购进甲种商品x件,乙种商品(20-x)件,根据题意得
190≤12x+8(20-x)≤200
………1分
解得7.5≤x≤10
∵x为非负整数
∴x取8,9,10
………2分
有三种进货方案:
①购甲种商品8件,乙种商品12件;
②购甲种商品9件,乙种商品11件;
③购甲种商品10件,乙种商品10件.
………3分
(2)设利润为w元,
则w=x×(14.5-12)+(20-x)×(10-8)=0.5x+40
………1分
因为0.5>0
所以W随X的增大而增大,
当X=10
W利润最大。
………2分
∴购甲种商品10件,乙种商品10件时,可获得最大利润,
最大利润是45万元.
………3分
(3)①全进甲,能购买3件,利润为(14.5-12)×3=7.5万元;
②全进乙,能购买5件,利润为(10-8)×5=10万元;………1分
③甲进1件,同时乙进4件,
利润为(14.5-12)×1+(10-8)×4=10.5万;
④甲进2件,同时乙进2件,利润为2.5×2+2×2=9万元;
⑤甲进3件,同时乙进1件,利润为2.5×3+2×1=9.5万元;
所以购甲种商品1件,乙种商品4件时,
可获得最大利润为10.5万元
……3分(③④⑤中写出2个给1分,都写全给2分)
26.
(本题9分,每问3分)
(1)
连接CB,CO,则CB∥y轴,
∴∠CBO=90°,
设O′为由O、B、C三点所确定圆的圆心.
则OC为⊙O′的直径.
………1分
由已知得OB=6,CB=8,
由勾股定理得OC=
………2分
半径OO′=5,S⊙O′=π?52=25π=78.50
………3分
(2)过点A作AD⊥x轴于点D,依题意,得∠BAD=30°,
在Rt△ABD中,设BD=x,则AB=2x,
由勾股定理得,AD=,
………1分
由题意知:OD=OB+BD=6+x,
在Rt△AOD中,OD=AD,6+x=,
………2分
∴x==3(+1)≈3(1.7+1)=8.1,
∴AB=2x=2×8.1=16.2
………3分
(3)过点A作AG⊥y轴于点G.
过点O′作O′E⊥OB于点E,并延长EO′交AG于点F.
由(1)知,OO′=5,由垂径定理得,OE=BE==3………1分
∴在Rt△OO′E中,由勾股定理得,O′E=
∵四边形FEDA为矩形.
∴EF=DA,而AD=×8.57≈14.6,
………2分
∴O′F=14.6-4=10.6>5,
∴直线AG与⊙O′相离,
A船不会进入海洋生物保护区.
………3分
27.
(本题9分,每问3分)
(1)证明:∵∠CAM=120°,
∴∠BAC=60°
………1分
且AD是∠CAM的平分线,
∴∠MAD=∠DAC=60°
………2分
又∵
圆O中
∠BAF=∠BCF=∠MAD
=60°
∠BFC=∠BAC=60°
∠BCF=∠BFC=60°,
∴△FBC是等边三角形.
………3分
(2)在AB上取一点G,使AG=AC
则由于∠BAC=60°,故△AGC是等边三角形,
………1分
从而∠BGC=∠FAC=120°,
又∠CBG=∠CFA,
BC=FC,
故△BCG≌△FCA,
………2分
从而BG=FA,又AG=AC,
∴AC+FA=AG+BG=AB.
………3分
28.
(本题9分,第一问2分,第(2)3分,第(3)4分)
解:(1)∵将抛物线y=﹣x2平移,平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),
∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3。
………1分
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4)。
………2分
(2)∠ACB与∠ABD相等。理由如下:
如图,∵y=﹣x2+2x+3,
∴当x=0时,y=3,即C点坐标为(0,3)。
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°。
………1分
在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,(提示:可过C向y轴作垂线求CD长,过D向x轴作垂线求BD长)
∴BC2+CD2=BD2。∴∠BCD=90°。
………2分
∴。
∵在△AOC中,∠AOC=90°,∴tan∠ACO=。
∴tan∠ACO=tan∠CBD。∴∠ACO=∠CBD。
∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD。
………3分
(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,
∴可设P点的坐标为(1,n)。
………1分
∵△ABC是锐角三角形,∴当△CDP与△ABC相似时,△CDP也是锐角三角形。
∴n<4,即点P只能在点D的下方。
………2分
又∵∠CDP=∠ABC=45°,∴D与B是对应点,分两种情况:
①如果△CDP∽△ABC,那么,
即。解得n=,
∴P点的坐标为(1,)。
………3分
②如果△CDP∽△CBA,那么,
即,解得n=。
∴P点的坐标为(1,)。
………4分
综上可知P点的坐标为(1,)或(1,)。
说明:学生试卷的解答题只要方法合理,可以酌情参考给分。
A.
B.
C.
D.
A
O
B
A
C
D
y
x
PAGE
?????
?九年级???数学试卷
时间:120分钟
总分:120分
一、选择题(本大题共10小题,每小题3分,共30分)
1.
2cos30°=( )
A.1
B.
C.
D.
2.一种花粉颗粒直径约为0.0000085米,数字0.0000085用科学记数法表示为( )
A.0.85×10﹣5
B.85×10﹣7
C.8.5×10﹣6
D.8.5×10﹣5
3.已知两个有理数a,b,如果ab>0且a+b<0,那么( )
A.a>0,b>0
B.a<0,b<
0
C.a、b同号
D.a、b异号,且正数的绝对值较大
4.一个正n边形的每一个外角都是72°,则n=( )
A.5
B.6
C.7
D.8
5.某商品打七折后价格为a元,则原价为( )
A.a元
B.a元
C.30%a元
D.a元
6.如果两个相似三角形对应边之比是1:4,那么它们的对应中线之比是( )
A.1:2
B.1:4
C.1:8
D.1:16
7.一次函数与二次函数在同一坐标系内的图象可能是(
)
8.如图所示的工件的主视图是
(
)
9.从分别写有数字1,2,3,4,5的5张卡片中依次取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是3的倍数的概率是(
)
A
.
B.
C.
D
.
10..抛物线中,b=4a,它的图象如图,有以下结论:①;②
③
④
⑤
⑥;其中正确的为(
)
A.①②
B.①④
C.①②⑥
D.①③⑤
二、填空题(本大题共10小题,每小题3分,共30分)
11.分解因式
=
.
12.函数=自变量的取值范围是
.
13.在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为
.
14.已知2x=3,2y=5,则22x﹣y的值是
.
15.若关于x的不等式组
HYPERLINK
"http://www..cn"
EMBED
Equation.DSMT4
解集为x<2,则a的取值范围是??
.
16.
关于x的分式方程的解是负数,则m的取值范围为
.
17.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 (结果保留根号).
18.如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=______度.
19.如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为______.
20.
如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM?,连接BN,当DM=1时,则△ABN的面积是
。
第17题
第18题图
第19题图
第20题图
三、解答题(本大题共8小题,共60分)
21.(5分)计算:一(-2)-1
22.(5分)先化简,再求值:,其中a=
23.(5分)为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t
≤20分钟的学生记为A类,20分钟<t
≤40分钟的学生记为B类,40分钟<t
≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)这次共抽查了
名学生进行调查统计,m=
%,
n=
%;
(2)请补全上面的条形图;
(3)如果该校共有1200名学生,请你估计该校C类学生约有多少人?
24.(9分)AB是⊙O的直径,弦DF⊥AB于E,连接BD.点C在BA的延长线上,且∠CDE=2∠B.连接CD,CD=8,AC=4.
(1)CD是⊙O的切线吗?请说明理由;
(2)求DF的长;
(3)求tan∠B.
25.
(9分)某公司经营甲、乙两种商品,每件甲种商品进价12万元,售价14.5万元.每件乙种商品进价8万元,售价10万元,且它们的进价和售价始终不变.现准备购进甲、乙两种商品共20件,所用资金不低于190万元不高于200万元.
(1)该公司有哪几种进货方案?
(2)该公司采用哪种进货方案可获得最大利润?最大利润是多少?
(3)利用(2)中所求得的最大利润再次进货,请直接写出获得最大利润的进货方案
26.(9分)在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
(1)求圆形区域的面积;
(2)某时刻海面上出现-渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离.(≈1.7,保留三个有效数字);
(3)当渔船A由(2)中位置向正西方向航行时,是否会进入海洋生物保护区?通过计算回答。
27.(9分)如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且AD与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由.
(2)请给出一个能反映AB、AC和FA的数量关系的一个等式,并说明你给出的等式成立.
28.(9分)
抛物线平移后的位置如图所示,点、坐标分别为(,0),(3,0),设平移后的抛物线与轴交于点,其顶点为。
(1)求平移后的抛物线的对称轴、解析式和点的坐标;
(2)和是否相等?请证明你的结论。
(3)点在平移后的抛物线的对称轴上,
且与相似,求点的坐标。
2018--2019学年度第一学期期未龙凤区答案
?????
?九年级???数学试卷
总分:120分
一.选择题:(共10题,每题3分,共30分)
1.B
2.
C
3.B
4.A
5.B
6.B
7.B
8.A
9.C
10.C
二.填空题:(共10题,每题3分,共30分)
11.a(1+a)(1-a)
12.x>1/2
13.2
14.9/5
15.a≥2
16.m>-8且m≠-4
17.
2
√Π/Π
18.
35
19.(
3/2
,√3/2)
20.
24/5
三.解答题(8道题,共60分)
21.(5分)解:原式=√2+1-
√2
+1/2
..............3分
=3/2
................5分
22.(5分)先化简,再求值。
解:原式=1/a+1
..............3分
结果等于√3/3
.............5分
23.
(5分)(1)50,
26,
14
.......共3分(每空1分)
(2)C类:50X20%=10人,补长方图略。.......1分
(3)1200X20%=240
........1分
24.
(本题9分,每问3分)
解:(1)连接DO.
∵OD=OB∴∠DBC=∠ODB
∴∠DOC=2∠DBO
………1分
∵∠CDE=2∠DBO
∴∠CDE=∠DOC
………2分
∴∠EDO+∠DOE=∠EDO
+∠CDE=
即∠CDO=
∴OD⊥CD
∴CD是⊙O切线
…………3分
(2)设⊙O的半径为R
在Rt△ODC中,
∠CDO=,
由勾股定理可知
即
∴R=6
………1分
∴OC=10
由面积公式可知
∴DE=
………2分
∵AB⊥DF,AB为⊙O直径
∴DF
=2DE=
…………3分
(3)由勾股定理求出OE=18/5
………1分
BE=48/5
………2分
在
Rt△DEB中,
tanB=DE/BE
=3/4
………3分
25.
(本题9分,每问3分。)
(1)设购进甲种商品x件,乙种商品(20-x)件,根据题意得
190≤12x+8(20-x)≤200
………1分
解得7.5≤x≤10
∵x为非负整数
∴x取8,9,10
………2分
有三种进货方案:
①购甲种商品8件,乙种商品12件;
②购甲种商品9件,乙种商品11件;
③购甲种商品10件,乙种商品10件.
………3分
(2)设利润为w元,
则w=x×(14.5-12)+(20-x)×(10-8)=0.5x+40
………1分
因为0.5>0
所以W随X的增大而增大,
当X=10
W利润最大。
………2分
∴购甲种商品10件,乙种商品10件时,可获得最大利润,
最大利润是45万元.
………3分
(3)①全进甲,能购买3件,利润为(14.5-12)×3=7.5万元;
②全进乙,能购买5件,利润为(10-8)×5=10万元;………1分
③甲进1件,同时乙进4件,
利润为(14.5-12)×1+(10-8)×4=10.5万;
④甲进2件,同时乙进2件,利润为2.5×2+2×2=9万元;
⑤甲进3件,同时乙进1件,利润为2.5×3+2×1=9.5万元;
所以购甲种商品1件,乙种商品4件时,
可获得最大利润为10.5万元
……3分(③④⑤中写出2个给1分,都写全给2分)
26.
(本题9分,每问3分)
(1)
连接CB,CO,则CB∥y轴,
∴∠CBO=90°,
设O′为由O、B、C三点所确定圆的圆心.
则OC为⊙O′的直径.
………1分
由已知得OB=6,CB=8,
由勾股定理得OC=
………2分
半径OO′=5,S⊙O′=π?52=25π=78.50
………3分
(2)过点A作AD⊥x轴于点D,依题意,得∠BAD=30°,
在Rt△ABD中,设BD=x,则AB=2x,
由勾股定理得,AD=,
………1分
由题意知:OD=OB+BD=6+x,
在Rt△AOD中,OD=AD,6+x=,
………2分
∴x==3(+1)≈3(1.7+1)=8.1,
∴AB=2x=2×8.1=16.2
………3分
(3)过点A作AG⊥y轴于点G.
过点O′作O′E⊥OB于点E,并延长EO′交AG于点F.
由(1)知,OO′=5,由垂径定理得,OE=BE==3………1分
∴在Rt△OO′E中,由勾股定理得,O′E=
∵四边形FEDA为矩形.
∴EF=DA,而AD=×8.57≈14.6,
………2分
∴O′F=14.6-4=10.6>5,
∴直线AG与⊙O′相离,
A船不会进入海洋生物保护区.
………3分
27.
(本题9分,每问3分)
(1)证明:∵∠CAM=120°,
∴∠BAC=60°
………1分
且AD是∠CAM的平分线,
∴∠MAD=∠DAC=60°
………2分
又∵
圆O中
∠BAF=∠BCF=∠MAD
=60°
∠BFC=∠BAC=60°
∠BCF=∠BFC=60°,
∴△FBC是等边三角形.
………3分
(2)在AB上取一点G,使AG=AC
则由于∠BAC=60°,故△AGC是等边三角形,
………1分
从而∠BGC=∠FAC=120°,
又∠CBG=∠CFA,
BC=FC,
故△BCG≌△FCA,
………2分
从而BG=FA,又AG=AC,
∴AC+FA=AG+BG=AB.
………3分
28.
(本题9分,第一问2分,第(2)3分,第(3)4分)
解:(1)∵将抛物线y=﹣x2平移,平移后的抛物线与x轴交于点A(﹣1,0)和点B(3,0),
∴平移后的抛物线的表达式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3,即y=﹣x2+2x+3。
………1分
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D的坐标为(1,4)。
………2分
(2)∠ACB与∠ABD相等。理由如下:
如图,∵y=﹣x2+2x+3,
∴当x=0时,y=3,即C点坐标为(0,3)。
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°。
………1分
在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,(提示:可过C向y轴作垂线求CD长,过D向x轴作垂线求BD长)
∴BC2+CD2=BD2。∴∠BCD=90°。
………2分
∴。
∵在△AOC中,∠AOC=90°,∴tan∠ACO=。
∴tan∠ACO=tan∠CBD。∴∠ACO=∠CBD。
∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD。
………3分
(3)∵点P在平移后的抛物线的对称轴上,而y=﹣x2+2x+3的对称轴为x=1,
∴可设P点的坐标为(1,n)。
………1分
∵△ABC是锐角三角形,∴当△CDP与△ABC相似时,△CDP也是锐角三角形。
∴n<4,即点P只能在点D的下方。
………2分
又∵∠CDP=∠ABC=45°,∴D与B是对应点,分两种情况:
①如果△CDP∽△ABC,那么,
即。解得n=,
∴P点的坐标为(1,)。
………3分
②如果△CDP∽△CBA,那么,
即,解得n=。
∴P点的坐标为(1,)。
………4分
综上可知P点的坐标为(1,)或(1,)。
说明:学生试卷的解答题只要方法合理,可以酌情参考给分。
A.
B.
C.
D.
A
O
B
A
C
D
y
x
PAGE
同课章节目录
