轴对称
图片预览





文档简介
(共24张PPT)
这个图形就叫做轴对称图形.
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,
这条直线就是它的对称轴.
这时,我们也说这个图形关于这条直线(成轴)对称 .
A′
A
B
C
B′
C′
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.
这条直线叫做对称轴.
折叠后重合的点是对应点,叫做对称点.
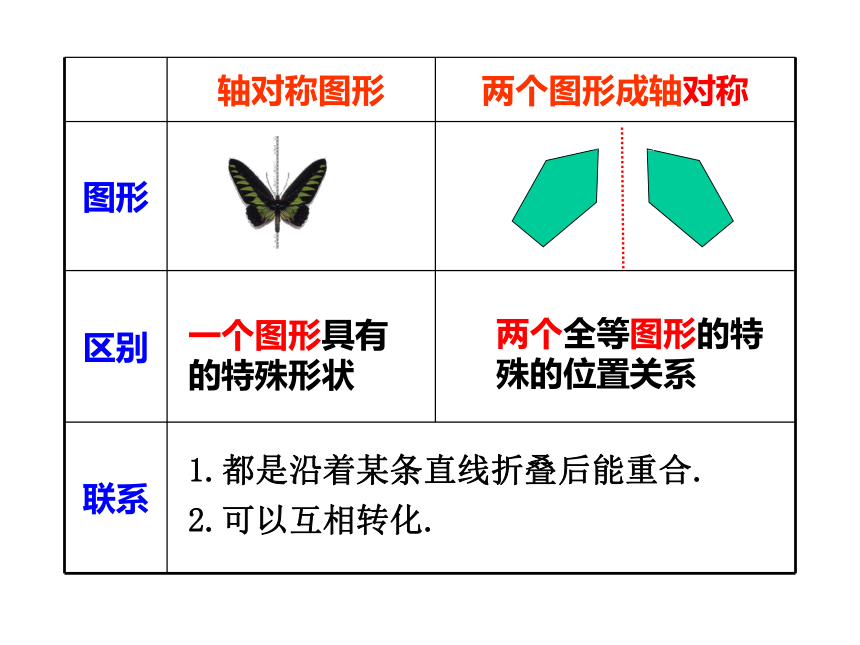
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
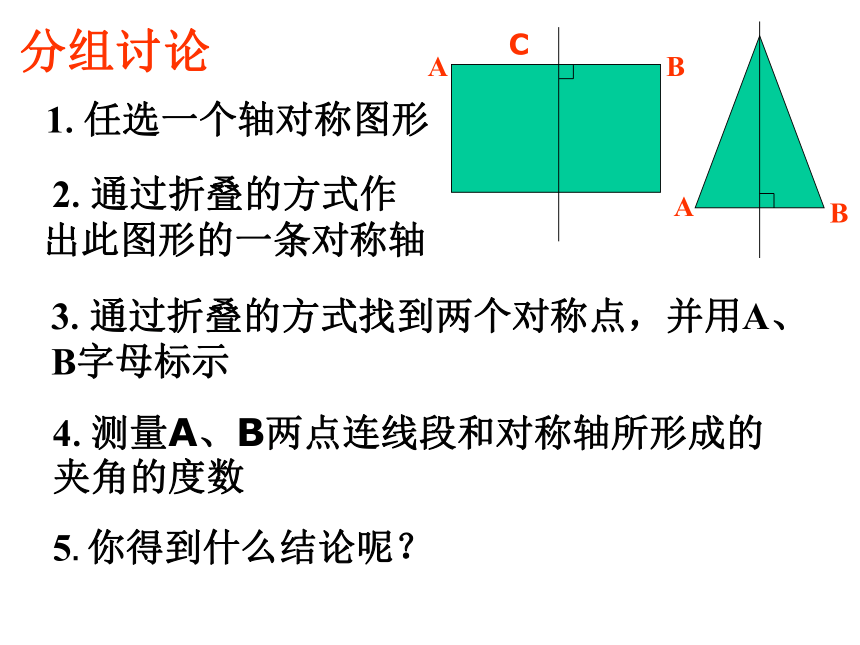
分组讨论
1.任选一个轴对称图形
A
B
A
B
C
2.通过折叠的方式作出此图形的一条对称轴
3.通过折叠的方式找到两个对称点,并用A、 B字母标示
4.测量A、B两点连线段和对称轴所形成的夹角的度数
5. 你得到什么结论呢?
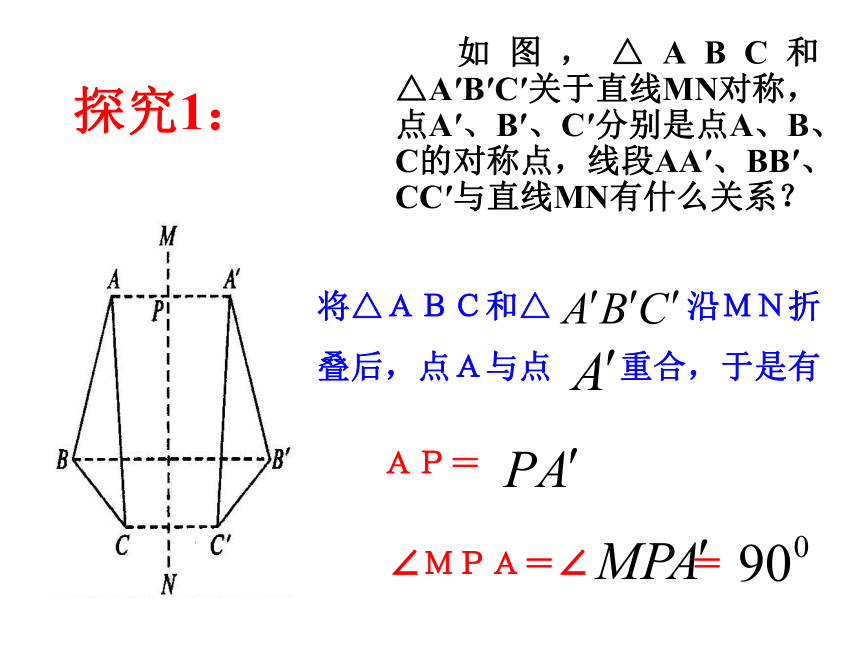
探究1:
如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?
AP=
∠MPA=∠ =
将△ABC和△ 沿MN折
叠后,点A与点 重合,于是有
探究
1、用上述方法,你还能得其它的结论吗?
D
E
BD=
CE=
∠MDB= ∠
∠MEC= ∠
2、由 ,
你能得什么结论?
AP=
∠MPA=∠ =
点P是 的中点
MN⊥
结论
对称轴所在的直线经过对称点所连线段的 中点,并且垂直于这条直线.
线段的垂直平分线
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)
轴对称的性质
1、如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
2、如果一 个图形是轴对称图形,那么对称轴是任何一对对应点所连线段的垂直平分线。
L垂直平分 ,
L垂直平分 ,
L垂直平分 .
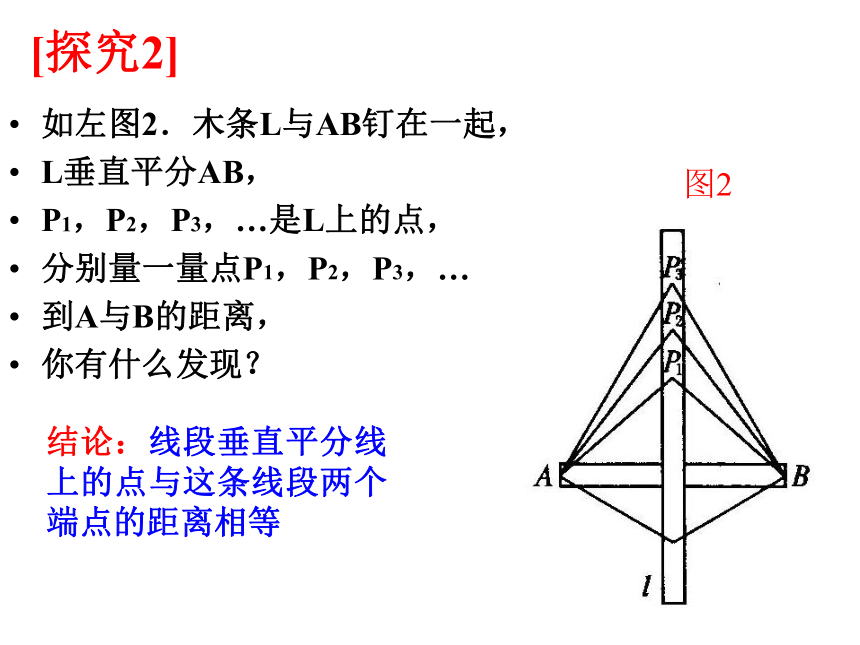
[探究2]
如左图2.木条L与AB钉在一起,
L垂直平分AB,
P1,P2,P3,…是L上的点,
分别量一量点P1,P2,P3,…
到A与B的距离,
你有什么发现?
图2
结论:线段垂直平分线上的点与这条线段两个端点的距离相等
线段垂直平分线上的点与这条线段两个端点距离相等.
你能证明这一结论吗
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
求证:PA=PB.
A
C
B
P
M
N
分析:(1)要证明PA=PB,
而△APC≌△BPC的条件由已知
故结论可证.
AC=BC,MN⊥AB,
可推知其能满足公理(SAS).
就需要证明PA,PB所在的△APC≌△BPC,
定理 线段垂直平分线上的点到这条线段两个端点距离相等.
提示:这个结论是经常用来证明两条线段相等的根据之一.
开启 智慧
A
C
B
P
M
N
定理应用格式:
如图,
∵AC=BC,MN⊥AB,
P是MN上任意一点(已知),
∴PA=PB
(线段垂直平分线上的点与这条线段两个端点距离相等).
思考:
如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
A
C
B
P
M
N
用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么?
C
B
A
只要AB=BC就可以
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
B
C
我能行
1
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
C
B
P
M
N
定理应用格式:
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上
(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
结论:
线段垂直平分线上的点
与这条线段两个端点的距离相等。
反之,与线段两个端点的距离相等的点
在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。
开启 智慧
拓展:
如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,
求△BCN的周长。
1、 如图,AD⊥BC,BD=DC,
点C在AE的垂直平分线上,
AB、AC 、CE 的长度有什么关系?
AB+BD 与DE有什么关系?
2、如图,AB=AC,MB=MC,
直线AM是线段BC的垂直平分线吗?
AB=AC=CE;
AB+BD=DE.
【P34:例】
[P38:12] 已知: △ABC中,边AB、 BC的垂直平分线交于点P。
求证:PA=PB=PC.
P
A
B
C
结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。
如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。
M
N
B
C
A
1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC 、CE 的长度有什么关系?AB+BD 与DE有什么关系?
2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
(4) 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
(1)线段是轴对称图形。
(2)垂直并且平分线段的直线叫做这条线段的垂直平分线。简称中垂线。
(3)线段垂直平分线上的点与这条线段的两个端点距离相等。
通过今天这节课你有什么收获
轴对称图形是说一个具有特殊形状的图形,不受位置的影响
轴对称是说两个图形的位置关系,受到位置的影响。
联系:⑴都能沿着某条直线折叠重合。
这条直线都对称轴。
⑵如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成轴对称;
反过来,把成轴对称的两个图形看成一个整体,那么它就是称对称图形。
通过图形理解了轴对称图形和关直线 成轴对称两个概念,请大家回忆一下,它们有什么区别和联系?
复习
区别:
作业:P36,习题 12.1
5 . 12
这个图形就叫做轴对称图形.
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,
这条直线就是它的对称轴.
这时,我们也说这个图形关于这条直线(成轴)对称 .
A′
A
B
C
B′
C′
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.
这条直线叫做对称轴.
折叠后重合的点是对应点,叫做对称点.
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
分组讨论
1.任选一个轴对称图形
A
B
A
B
C
2.通过折叠的方式作出此图形的一条对称轴
3.通过折叠的方式找到两个对称点,并用A、 B字母标示
4.测量A、B两点连线段和对称轴所形成的夹角的度数
5. 你得到什么结论呢?
探究1:
如图,△ABC和△A′B′C′关于直线MN对称,点A′、B′、C′分别是点A、B、C的对称点,线段AA′、BB′、CC′与直线MN有什么关系?
AP=
∠MPA=∠ =
将△ABC和△ 沿MN折
叠后,点A与点 重合,于是有
探究
1、用上述方法,你还能得其它的结论吗?
D
E
BD=
CE=
∠MDB= ∠
∠MEC= ∠
2、由 ,
你能得什么结论?
AP=
∠MPA=∠ =
点P是 的中点
MN⊥
结论
对称轴所在的直线经过对称点所连线段的 中点,并且垂直于这条直线.
线段的垂直平分线
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)
轴对称的性质
1、如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
2、如果一 个图形是轴对称图形,那么对称轴是任何一对对应点所连线段的垂直平分线。
L垂直平分 ,
L垂直平分 ,
L垂直平分 .
[探究2]
如左图2.木条L与AB钉在一起,
L垂直平分AB,
P1,P2,P3,…是L上的点,
分别量一量点P1,P2,P3,…
到A与B的距离,
你有什么发现?
图2
结论:线段垂直平分线上的点与这条线段两个端点的距离相等
线段垂直平分线上的点与这条线段两个端点距离相等.
你能证明这一结论吗
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
求证:PA=PB.
A
C
B
P
M
N
分析:(1)要证明PA=PB,
而△APC≌△BPC的条件由已知
故结论可证.
AC=BC,MN⊥AB,
可推知其能满足公理(SAS).
就需要证明PA,PB所在的△APC≌△BPC,
定理 线段垂直平分线上的点到这条线段两个端点距离相等.
提示:这个结论是经常用来证明两条线段相等的根据之一.
开启 智慧
A
C
B
P
M
N
定理应用格式:
如图,
∵AC=BC,MN⊥AB,
P是MN上任意一点(已知),
∴PA=PB
(线段垂直平分线上的点与这条线段两个端点距离相等).
思考:
如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
A
C
B
P
M
N
用一根木棒和一根弹性均匀的橡皮筋,做一 个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保持射出去的方向与木棒垂直呢?为什么?
C
B
A
只要AB=BC就可以
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
B
C
我能行
1
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
A
C
B
P
M
N
定理应用格式:
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上
(与一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.
结论:
线段垂直平分线上的点
与这条线段两个端点的距离相等。
反之,与线段两个端点的距离相等的点
在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。
开启 智慧
拓展:
如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,
求△BCN的周长。
1、 如图,AD⊥BC,BD=DC,
点C在AE的垂直平分线上,
AB、AC 、CE 的长度有什么关系?
AB+BD 与DE有什么关系?
2、如图,AB=AC,MB=MC,
直线AM是线段BC的垂直平分线吗?
AB=AC=CE;
AB+BD=DE.
【P34:例】
[P38:12] 已知: △ABC中,边AB、 BC的垂直平分线交于点P。
求证:PA=PB=PC.
P
A
B
C
结论:三角形三边的垂直平分线交于一点,并且这点到三个顶点的距离相等。
如图,七(1)班与七(2)班两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且PM=PN,请你用折纸的方法找出P点并说明理由。
M
N
B
C
A
1、 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC 、CE 的长度有什么关系?AB+BD 与DE有什么关系?
2、如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
(4) 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
(1)线段是轴对称图形。
(2)垂直并且平分线段的直线叫做这条线段的垂直平分线。简称中垂线。
(3)线段垂直平分线上的点与这条线段的两个端点距离相等。
通过今天这节课你有什么收获
轴对称图形是说一个具有特殊形状的图形,不受位置的影响
轴对称是说两个图形的位置关系,受到位置的影响。
联系:⑴都能沿着某条直线折叠重合。
这条直线都对称轴。
⑵如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成轴对称;
反过来,把成轴对称的两个图形看成一个整体,那么它就是称对称图形。
通过图形理解了轴对称图形和关直线 成轴对称两个概念,请大家回忆一下,它们有什么区别和联系?
复习
区别:
作业:P36,习题 12.1
5 . 12
