华师大版数学九年级上册22.2.3公式法 课件(共25张PPT)
文档属性
| 名称 | 华师大版数学九年级上册22.2.3公式法 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 07:32:12 | ||
图片预览








文档简介
(共25张PPT)
二、用配方解一元二次方程的步骤是什么?
回顾与复习
1
一、用配方法解一元二次方程:
2、把常数项移到方程右边;
3、在方程的两边各加上一次项系数绝对值的一半的平方,使左边成为完全平方;
4、如果方程的右边整理后是非负数,用直接开平方法解之,如果右边是个负数,则指出原方程无实根。
1、若二次项系数不是1,把二次项系数化为1(方程两边都除以二次项系数);
用直接开平方法和配方法解一元二次方程,计算比较麻烦,能否研究出一种更好的方法,迅速求得一元二次方程的实数根呢?
公式法是这样生产的
你能用配方法解方程ax2+bx+c=0(a≠0)吗?
心动
不如行动
1.化1:把二次项系数化为1;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
2.移项:把常数项移到方程的右边;
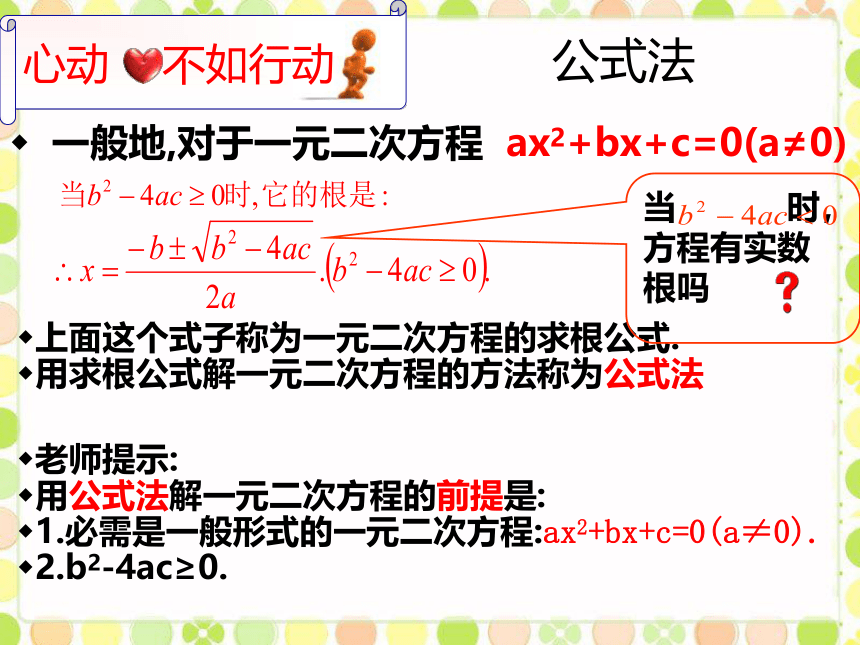
公式法
一般地,对于一元二次方程
ax2+bx+c=0(a≠0)
心动
不如行动
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法
老师提示:
用公式法解一元二次方程的前提是:
1.必需是一般形式的一元二次方程:ax2+bx+c=0(a≠0).
2.b2-4ac≥0.
当
时,方程有实数根吗
当 时,方程没有实数根.
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
方程根的情况(根的判别式)
公式法
例1、用公式法解方程
5x2-4x-12=0
1.变形:化已知方程为一般形式;
3.计算:
b2-4ac的值;
4.代入:把有关数值代入公式计算;
5.定根:写出原方程的根.
2.确定系数:用a,b,c写出各项系数;
学习是件很愉快的事
例2.用公式法解方程2x2+5x-3=0
解:
a=2
b=5
c=
-3
∴
b2-4ac=52-4×2×(-3)=49
∴
x
=
=
=
即
x1=
-
3
x2=
求根公式
:
X=
(a≠0,
b2-4ac≥0)
解:a=
,b=
,c
=
.
b2-4ac=
=
.
x=
=
=
.
即
x1=
,
x2=
.
(口答)填空:用公式法解方程
2x2+x-6=0
2
1
-6
12-4×2×(-6)
49
-2
求根公式
:
X=
(a≠0,
b2-4ac≥0)
a=
,b=
,c
=
.
b2-4ac=
=
.
x=
=
=
.
即
x1=
,
x2=
.
例3:用公式法解方程x2+4x=2
1
4
-2
42-4×1×(-2)
24
求根公式
:
X=
(a≠0,
b2-4ac≥0)
解:移项,得
x2+4x-2=0
这里的a、b、c的值是什么?
3、代入求根公式
:
X=
(a≠0,
b2-4ac≥0)
1、把方程化成一般形式,并写出a,b,c的值。
2、求出b2-4ac的值。
用公式法解一元二次方程的一般步骤:
求根公式
:
X=
4、写出方程的解:
x1=?,
x2=?
(a≠0,
b2-4ac≥0)
用公式法解下列方程:
1、x2
+2x
=5
2、
6t2
-5
=13t
(x1=-1+
,x2=-1-
)
(t1=
,t2=
-
)
例4
解方程:
解:
结论:当
时,一元二次方程有两个
相等的实数根.
解:去括号,化简为一般式:
例
5
解方程:
这里
方程没有实数解。
解:
师生互动
巩固新知
解:
解:化为一般式
解:化为一般式
求根公式
:
X=
由配方法解一般的一元二次方程
ax2+bx+c=0
(a≠0)
若
b2-4ac≥0 得
1、把方程化成一般形式,并写出a,b,c的值。
2、求出b2-4ac的值。
3、代入求根公式
:
用公式法解一元二次方程的一般步骤:
小结
4、写出方程的解:
x1=?,
x2=?
(a≠0,
b2-4ac≥0)
X=
独立
作业
知识的升华
祝你成功!
1、关于x的一元二次方程
有两个实根,则m的取值范围是——
.
注意:一元二次方程有实根,说明方程可能有两个不等实根或两个相等实根的两种情况。
拓展延伸
解:
∴
2、关于x的一元二次方程kx2-2x-1=0有两个不等的实根,则k的取值范围是
(
)
A.k>-1
B.
k>-1
且k≠
0
C.
k<1
D.
k<1
且k≠0
解:∵
>0
∴k>-1
又∵k≠0
∴
k>-1且k≠0
B
A
m取什么值时,方程
x2+(2m+1)x+m2-4=0有两个相等的实数解
思考题
想一想:
关于一元二次方程
,当
a,b,c满足什么条件时,方程的两根互
为相反数?
解:
一元二次方程
的解为:
提高练习
解:
已知方程
求c和x的值.
五、小结
用公式法解一元二次方程的关键是解题步骤:
3.最后代入公式
当
时,有两个实数根
当
时,方程无实数解
1.先写出a,b,c
2.再求出
二、用配方解一元二次方程的步骤是什么?
回顾与复习
1
一、用配方法解一元二次方程:
2、把常数项移到方程右边;
3、在方程的两边各加上一次项系数绝对值的一半的平方,使左边成为完全平方;
4、如果方程的右边整理后是非负数,用直接开平方法解之,如果右边是个负数,则指出原方程无实根。
1、若二次项系数不是1,把二次项系数化为1(方程两边都除以二次项系数);
用直接开平方法和配方法解一元二次方程,计算比较麻烦,能否研究出一种更好的方法,迅速求得一元二次方程的实数根呢?
公式法是这样生产的
你能用配方法解方程ax2+bx+c=0(a≠0)吗?
心动
不如行动
1.化1:把二次项系数化为1;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
2.移项:把常数项移到方程的右边;
公式法
一般地,对于一元二次方程
ax2+bx+c=0(a≠0)
心动
不如行动
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法
老师提示:
用公式法解一元二次方程的前提是:
1.必需是一般形式的一元二次方程:ax2+bx+c=0(a≠0).
2.b2-4ac≥0.
当
时,方程有实数根吗
当 时,方程没有实数根.
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
方程根的情况(根的判别式)
公式法
例1、用公式法解方程
5x2-4x-12=0
1.变形:化已知方程为一般形式;
3.计算:
b2-4ac的值;
4.代入:把有关数值代入公式计算;
5.定根:写出原方程的根.
2.确定系数:用a,b,c写出各项系数;
学习是件很愉快的事
例2.用公式法解方程2x2+5x-3=0
解:
a=2
b=5
c=
-3
∴
b2-4ac=52-4×2×(-3)=49
∴
x
=
=
=
即
x1=
-
3
x2=
求根公式
:
X=
(a≠0,
b2-4ac≥0)
解:a=
,b=
,c
=
.
b2-4ac=
=
.
x=
=
=
.
即
x1=
,
x2=
.
(口答)填空:用公式法解方程
2x2+x-6=0
2
1
-6
12-4×2×(-6)
49
-2
求根公式
:
X=
(a≠0,
b2-4ac≥0)
a=
,b=
,c
=
.
b2-4ac=
=
.
x=
=
=
.
即
x1=
,
x2=
.
例3:用公式法解方程x2+4x=2
1
4
-2
42-4×1×(-2)
24
求根公式
:
X=
(a≠0,
b2-4ac≥0)
解:移项,得
x2+4x-2=0
这里的a、b、c的值是什么?
3、代入求根公式
:
X=
(a≠0,
b2-4ac≥0)
1、把方程化成一般形式,并写出a,b,c的值。
2、求出b2-4ac的值。
用公式法解一元二次方程的一般步骤:
求根公式
:
X=
4、写出方程的解:
x1=?,
x2=?
(a≠0,
b2-4ac≥0)
用公式法解下列方程:
1、x2
+2x
=5
2、
6t2
-5
=13t
(x1=-1+
,x2=-1-
)
(t1=
,t2=
-
)
例4
解方程:
解:
结论:当
时,一元二次方程有两个
相等的实数根.
解:去括号,化简为一般式:
例
5
解方程:
这里
方程没有实数解。
解:
师生互动
巩固新知
解:
解:化为一般式
解:化为一般式
求根公式
:
X=
由配方法解一般的一元二次方程
ax2+bx+c=0
(a≠0)
若
b2-4ac≥0 得
1、把方程化成一般形式,并写出a,b,c的值。
2、求出b2-4ac的值。
3、代入求根公式
:
用公式法解一元二次方程的一般步骤:
小结
4、写出方程的解:
x1=?,
x2=?
(a≠0,
b2-4ac≥0)
X=
独立
作业
知识的升华
祝你成功!
1、关于x的一元二次方程
有两个实根,则m的取值范围是——
.
注意:一元二次方程有实根,说明方程可能有两个不等实根或两个相等实根的两种情况。
拓展延伸
解:
∴
2、关于x的一元二次方程kx2-2x-1=0有两个不等的实根,则k的取值范围是
(
)
A.k>-1
B.
k>-1
且k≠
0
C.
k<1
D.
k<1
且k≠0
解:∵
>0
∴k>-1
又∵k≠0
∴
k>-1且k≠0
B
A
m取什么值时,方程
x2+(2m+1)x+m2-4=0有两个相等的实数解
思考题
想一想:
关于一元二次方程
,当
a,b,c满足什么条件时,方程的两根互
为相反数?
解:
一元二次方程
的解为:
提高练习
解:
已知方程
求c和x的值.
五、小结
用公式法解一元二次方程的关键是解题步骤:
3.最后代入公式
当
时,有两个实数根
当
时,方程无实数解
1.先写出a,b,c
2.再求出
