第四章 概率与统计 基础夯实__2021-2022学年高二数学人教B版(2019)选择性必修第二册单元测试卷(Word含解析)
文档属性
| 名称 | 第四章 概率与统计 基础夯实__2021-2022学年高二数学人教B版(2019)选择性必修第二册单元测试卷(Word含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 820.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览



文档简介
第四章
概率与统计
基础夯实——2021-2022学年高二数学人教B版(2019)选择性必修第二册单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
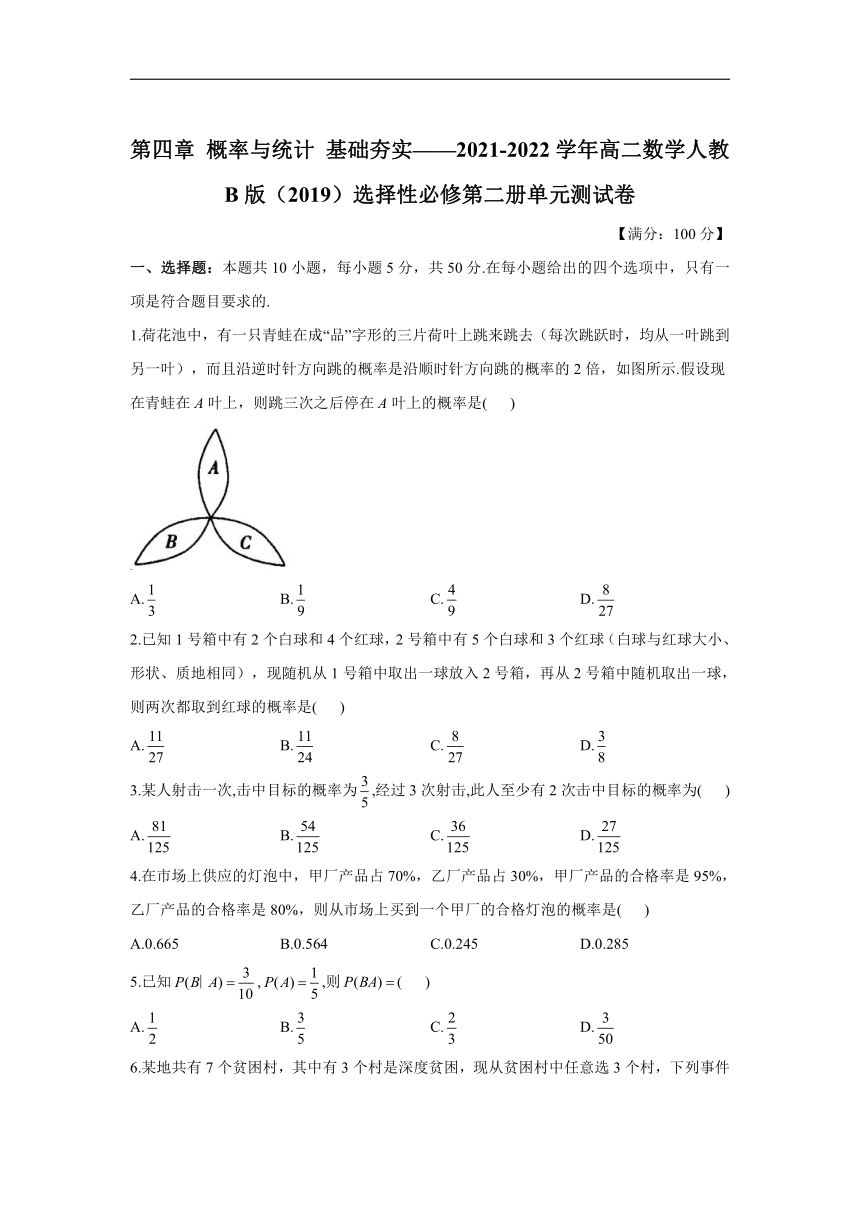
1.荷花池中,有一只青蛙在成“品”字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且沿逆时针方向跳的概率是沿顺时针方向跳的概率的2倍,如图所示.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是(
)
A.
B.
C.
D.
2.已知1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球(白球与红球大小、形状、质地相同),现随机从1号箱中取出一球放入2号箱,再从2号箱中随机取出一球,则两次都取到红球的概率是(
)
A.
B.
C.
D.
3.某人射击一次,击中目标的概率为,经过3次射击,此人至少有2次击中目标的概率为(
)
A.
B.
C.
D.
4.在市场上供应的灯泡中,甲厂产品占70%,乙厂产品占30%,甲厂产品的合格率是95%,乙厂产品的合格率是80%,则从市场上买到一个甲厂的合格灯泡的概率是(
)
A.0.665
B.0.564
C.0.245
D.0.285
5.已知,,则(
)
A.
B.
C.
D.
6.某地共有7个贫困村,其中有3个村是深度贫困,现从贫困村中任意选3个村,下列事件中概率为的是(
)
A.至少有1个深度贫困村
B.有1个或2个深度贫困村
C.有2个或3个深度贫困村
D.恰有2个深度贫困村
7.一个袋中放有大小、形状均相同的小球,其中红球1个、黑球2个.现从中随机取出小球,当有放回地依次取出2个小球时,记取出的红球数为;当无放回地依次取出2个小球时,记取出的红球数为,则(
)
A.,
B.,
C.,
D.,
8.设随机变量的分布列为,,…,n,且,则的值为(
)
A.8
B.
C.12
D.16
9.已知随机变量,若,则和分别是(
)
A.2和2.4
B.4和2.4
C.6和2.4
D.4和5.6
10.设随机变量,且X的均值与方差分别是2.4和1.44,则(
)
A.,
B.,
C.,
D.,
二、填空题:本题共5小题,每小题5分,共25分.
11.甲、乙两个实习生每人加工一个零件,加工的零件为一等品的概率分别为和,两人加工的零件是否为一等品互不影响,则这两个零件中恰有一个一等品的概率为
__________.
12.某人有8把颜色和外形相同的钥匙,其中只有一把能打开家门.一次该人醉酒回家,每次从8把钥匙中随便拿一把开门,试用后又不加记号放回,则该人第三次打开家门的概率是__________.
13.已知离散型随机变量的分布列如下表:
1
2
3
4
5
6
P
0.2
x
0.25
0.1
0.15
0.2
则__________.
14.甲、乙两队参加某次对抗赛,其中一轮有3个抢答题,比赛规定:对于每个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分).若X是甲队在该轮比赛获胜时的得分(分数高者胜),则X的所有可能取值是_____________.
15.调查了某地若干户家庭的年收入(单位:万元)和年饮食支出(单位:万元),调查显示年收入与年饮食支出具有线性相关关系,并由调查数据得到对的回归直线方程:.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)粒子A位于数轴上处,粒子B位于处,这两个粒子每秒向左或向右移动一个单位,且向右移动的概率是,向左移动的概率是.
(1)求3s后粒子A在处的概率;
(2)若粒子A,B同时移动,求2s后,粒子A,B均在处的概率.
17.
(15分)从装有2个红球和6个白球(球除颜色外,其余完全相同)的袋子中,每次不放回地摸出2个球作为一次试验,直到摸出的球中有红球时试验结束.
(1)求第一次试验恰好摸到1个红球和1个白球的概率;
(2)记试验次数为X,求X的分布列.
答案以及解析
1.答案:A
解析:由题意,知青蛙沿逆时针方向跳的概率是,沿顺时针方向跳的概率是.青蛙跳三次要回到A叶上只有两条途径:第一条,按,此时停在A叶上的概率.第二条,按,此时停在A叶上的概率.所以跳三次之后停在A叶上的概率.
2.答案:C
解析:设“从1号箱中取到红球放入2号箱”为事件A,“从2号箱中取到红球”为事件B.由题意,知,,所以,所以两次都取到红球的概率为.故选C.
3.答案:A
解析:所求概率为.
4.答案:A
解析:记事件A为“甲厂产品”,事件B为“合格产品”,则,,,所以.
5.答案:D
解析:易知,故选D.
6.答案:B
解析:若用X表示所选的3个村庄中深度贫困村的个数,则,所以,,,,所以,即任意选3个村中有1个或2个深度贫困村时的概率为.故选B.
7.答案:B
解析:易知,故,.的取值范围为,,,故,,故,.故选B.
8.答案:A
解析:由题意可知,,,.
9.答案:B
解析:因为,所以,.又,所以,所以,.
10.答案:B
解析:由题意,得,,,,.
11.答案:
解析:设事件“甲实习生加工的零件为一等品”,事件“乙实习生加工的零件为一等品”,则,,所以这两个零件中恰有一个一等品的概率为.
12.答案:
解析:易知每次打开家门的概率为,则该人第三次打开家门的概率为.
13.答案:0.45
解析:由分布列的性质,得,解得,所以.
14.答案:-1,0,1,2,3
解析:,甲抢到1个题但回答错误,而乙抢到2个题都回答错误;,甲没抢到题,或甲抢到2个题只答对1个题;,甲抢到1个题且回答正确,或甲抢到3个题答对2个题;,甲抢到2个题均回答正确;,甲抢到3个题均回答正确.
15.答案:0.254
解析:解:∵对的回归直线方程.
∴当家庭年收入增加1万元时,,
∵.
故年饮食支出平均增加0.254万元.
故答案为:0.254.
16.答案:(1)3s后粒子A在处,则粒子A在三次移动中有一次向左移动,
故所求概率为.
(2)由题意,知粒子A在两次移动中均向右,粒子B向左、向右各移动一次,
故所求概率为.
17.答案:(1)记“第一次试验恰好摸到1个红球和1个白球”为事件A,则.
(2)由题意,知X的取值范围为,则
,
,
,
,
所以X的分布列为
X
1
2
3
4
P
概率与统计
基础夯实——2021-2022学年高二数学人教B版(2019)选择性必修第二册单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.荷花池中,有一只青蛙在成“品”字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且沿逆时针方向跳的概率是沿顺时针方向跳的概率的2倍,如图所示.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是(
)
A.
B.
C.
D.
2.已知1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球(白球与红球大小、形状、质地相同),现随机从1号箱中取出一球放入2号箱,再从2号箱中随机取出一球,则两次都取到红球的概率是(
)
A.
B.
C.
D.
3.某人射击一次,击中目标的概率为,经过3次射击,此人至少有2次击中目标的概率为(
)
A.
B.
C.
D.
4.在市场上供应的灯泡中,甲厂产品占70%,乙厂产品占30%,甲厂产品的合格率是95%,乙厂产品的合格率是80%,则从市场上买到一个甲厂的合格灯泡的概率是(
)
A.0.665
B.0.564
C.0.245
D.0.285
5.已知,,则(
)
A.
B.
C.
D.
6.某地共有7个贫困村,其中有3个村是深度贫困,现从贫困村中任意选3个村,下列事件中概率为的是(
)
A.至少有1个深度贫困村
B.有1个或2个深度贫困村
C.有2个或3个深度贫困村
D.恰有2个深度贫困村
7.一个袋中放有大小、形状均相同的小球,其中红球1个、黑球2个.现从中随机取出小球,当有放回地依次取出2个小球时,记取出的红球数为;当无放回地依次取出2个小球时,记取出的红球数为,则(
)
A.,
B.,
C.,
D.,
8.设随机变量的分布列为,,…,n,且,则的值为(
)
A.8
B.
C.12
D.16
9.已知随机变量,若,则和分别是(
)
A.2和2.4
B.4和2.4
C.6和2.4
D.4和5.6
10.设随机变量,且X的均值与方差分别是2.4和1.44,则(
)
A.,
B.,
C.,
D.,
二、填空题:本题共5小题,每小题5分,共25分.
11.甲、乙两个实习生每人加工一个零件,加工的零件为一等品的概率分别为和,两人加工的零件是否为一等品互不影响,则这两个零件中恰有一个一等品的概率为
__________.
12.某人有8把颜色和外形相同的钥匙,其中只有一把能打开家门.一次该人醉酒回家,每次从8把钥匙中随便拿一把开门,试用后又不加记号放回,则该人第三次打开家门的概率是__________.
13.已知离散型随机变量的分布列如下表:
1
2
3
4
5
6
P
0.2
x
0.25
0.1
0.15
0.2
则__________.
14.甲、乙两队参加某次对抗赛,其中一轮有3个抢答题,比赛规定:对于每个题,没有抢到题的队伍得0分,抢到题并回答正确的得1分,抢到题但回答错误的扣1分(即得-1分).若X是甲队在该轮比赛获胜时的得分(分数高者胜),则X的所有可能取值是_____________.
15.调查了某地若干户家庭的年收入(单位:万元)和年饮食支出(单位:万元),调查显示年收入与年饮食支出具有线性相关关系,并由调查数据得到对的回归直线方程:.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)粒子A位于数轴上处,粒子B位于处,这两个粒子每秒向左或向右移动一个单位,且向右移动的概率是,向左移动的概率是.
(1)求3s后粒子A在处的概率;
(2)若粒子A,B同时移动,求2s后,粒子A,B均在处的概率.
17.
(15分)从装有2个红球和6个白球(球除颜色外,其余完全相同)的袋子中,每次不放回地摸出2个球作为一次试验,直到摸出的球中有红球时试验结束.
(1)求第一次试验恰好摸到1个红球和1个白球的概率;
(2)记试验次数为X,求X的分布列.
答案以及解析
1.答案:A
解析:由题意,知青蛙沿逆时针方向跳的概率是,沿顺时针方向跳的概率是.青蛙跳三次要回到A叶上只有两条途径:第一条,按,此时停在A叶上的概率.第二条,按,此时停在A叶上的概率.所以跳三次之后停在A叶上的概率.
2.答案:C
解析:设“从1号箱中取到红球放入2号箱”为事件A,“从2号箱中取到红球”为事件B.由题意,知,,所以,所以两次都取到红球的概率为.故选C.
3.答案:A
解析:所求概率为.
4.答案:A
解析:记事件A为“甲厂产品”,事件B为“合格产品”,则,,,所以.
5.答案:D
解析:易知,故选D.
6.答案:B
解析:若用X表示所选的3个村庄中深度贫困村的个数,则,所以,,,,所以,即任意选3个村中有1个或2个深度贫困村时的概率为.故选B.
7.答案:B
解析:易知,故,.的取值范围为,,,故,,故,.故选B.
8.答案:A
解析:由题意可知,,,.
9.答案:B
解析:因为,所以,.又,所以,所以,.
10.答案:B
解析:由题意,得,,,,.
11.答案:
解析:设事件“甲实习生加工的零件为一等品”,事件“乙实习生加工的零件为一等品”,则,,所以这两个零件中恰有一个一等品的概率为.
12.答案:
解析:易知每次打开家门的概率为,则该人第三次打开家门的概率为.
13.答案:0.45
解析:由分布列的性质,得,解得,所以.
14.答案:-1,0,1,2,3
解析:,甲抢到1个题但回答错误,而乙抢到2个题都回答错误;,甲没抢到题,或甲抢到2个题只答对1个题;,甲抢到1个题且回答正确,或甲抢到3个题答对2个题;,甲抢到2个题均回答正确;,甲抢到3个题均回答正确.
15.答案:0.254
解析:解:∵对的回归直线方程.
∴当家庭年收入增加1万元时,,
∵.
故年饮食支出平均增加0.254万元.
故答案为:0.254.
16.答案:(1)3s后粒子A在处,则粒子A在三次移动中有一次向左移动,
故所求概率为.
(2)由题意,知粒子A在两次移动中均向右,粒子B向左、向右各移动一次,
故所求概率为.
17.答案:(1)记“第一次试验恰好摸到1个红球和1个白球”为事件A,则.
(2)由题意,知X的取值范围为,则
,
,
,
,
所以X的分布列为
X
1
2
3
4
P
