22.3.3建立适当坐标系解决实际问题—人教版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 22.3.3建立适当坐标系解决实际问题—人教版九年级数学上册课时作业(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 365.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 11:27:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册课时作业
第二十二章 二次函数
22.3 实际问题与二次函数
第3课时 建立适当坐标系解决实际问题
1.
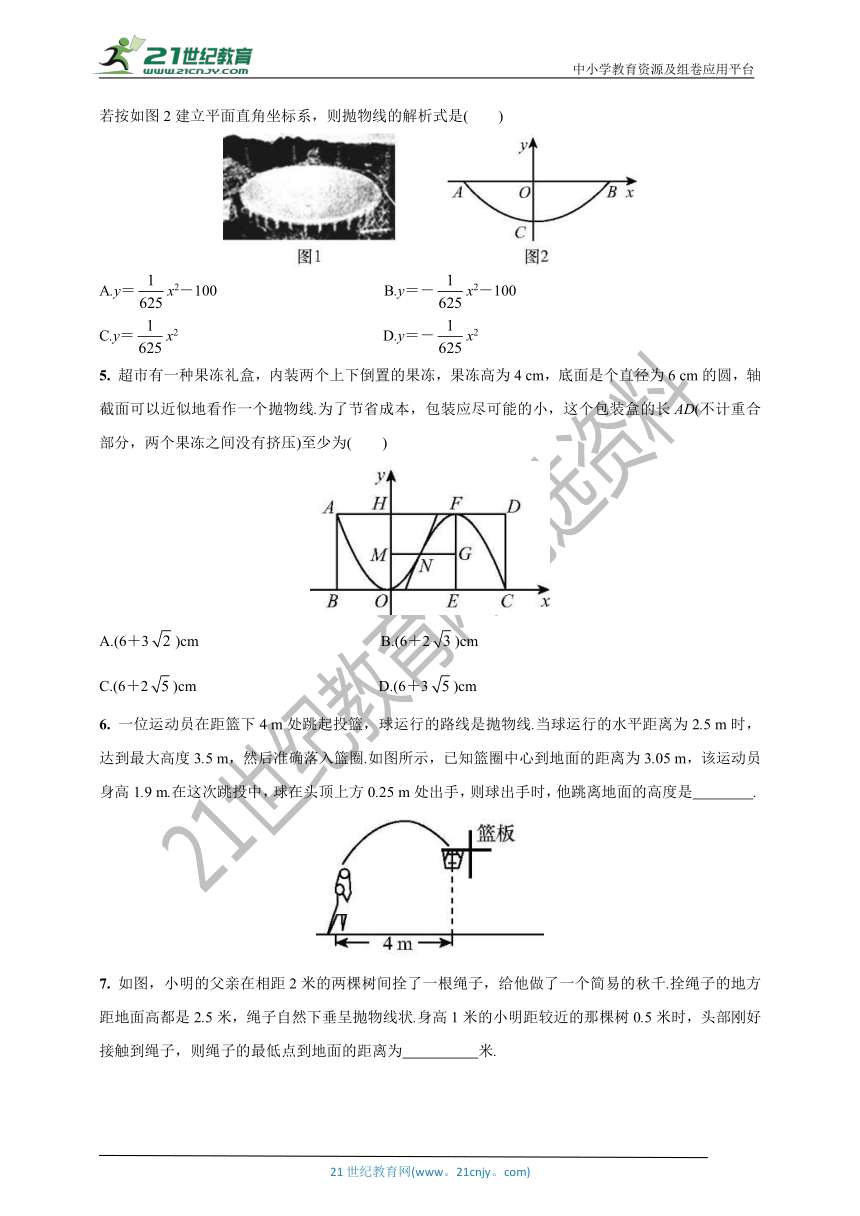
如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,则在线段AB上离中心M处5米的地方,桥的高度是( )
A.15米
B.14米
C.13米
D.12米
2.
某公园草坪的防护栏是由150段形状相同的抛物线组成的.如图,为了牢固起见,每段护栏需要间距0.4
m加设一根不锈钢的支柱,防护栏的最高点距底部0.5
m,则这条防护栏需要不锈钢支柱的总长度至少为( )
A.240
m
B.200
m
C.160
m
D.150
m
3.
小明学习了这节课后,课下竖直向上抛一个小球做实验,小球上升的高度h(m)与运动时间t(s)的函数关系式为h=at2+bt,图象如图所示.若小球在抛出后第2
s与第6
s时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3
s
B.第3.9
s
C.第4.5
s
D.第6.5
s
4.
位于中国贵州省内的射电望远镜(FAST)是目前世界上口径最大、精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点C到口径面AB的距离是100米.若按如图2建立平面直角坐标系,则抛物线的解析式是( )
A.y=x2-100
B.y=-x2-100
C.y=x2
D.y=-x2
5.
超市有一种果冻礼盒,内装两个上下倒置的果冻,果冻高为4
cm,底面是个直径为6
cm的圆,轴截面可以近似地看作一个抛物线.为了节省成本,包装应尽可能的小,这个包装盒的长AD(不计重合部分,两个果冻之间没有挤压)至少为( )
A.(6+3)cm
B.(6+2)cm
C.(6+2)cm
D.(6+3)cm
6.
一位运动员在距篮下4
m处跳起投篮,球运行的路线是抛物线.当球运行的水平距离为2.5
m时,达到最大高度3.5
m,然后准确落入篮圈.如图所示,已知篮圈中心到地面的距离为3.05
m,该运动员身高1.9
m.在这次跳投中,球在头顶上方0.25
m处出手,则球出手时,他跳离地面的高度是
.?
7.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状.身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点到地面的距离为
米.?
8.
图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86
m,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为
m.?
9.
如图,丁丁设计了一款杯子,杯子的上半部分是二次函数y=2x2+8的图象的一部分.若AB=4,DE=3,求杯子的高CE.
10.
如图1,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的平面直角坐标系,这条绳子可以用y=x2-x+3表示.
(1)求这条绳子的最低点到地面的距离;
(2)现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑(如图2),已知立柱EF到AB的距离为3
m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1
m,到地面的距离为1.8
m,求立柱EF的长.
11.
某校进行了一场足球比赛,比赛场上守门员小王在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的解析式.
(2)足球第一次落地点C距守门员多少米?(取4≈7)
(3)运动员乙要抢到足球第二个落地点D,他应再向前跑多少米?(取2≈5)
参
考
答
案
1.
A
2.
A
3.
B
4.
A
5.
A
6.
0.1
m
7.
0.5
8.
2.7
9.
解:由题意可得,点D的坐标为(0,8),∵AB=4,∴点B的横坐标为2,当x=2时,y=2×4+8=16,即B(2,16),∴CD=16-8=8,∴CE=CD+DE=8+3=11.
10.
解:(1)因为y=x2-x+3=(x-4)2+,所以抛物线的顶点坐标为(4,),则这条绳子的最低点到地面的距离为
m.
(2)对于y=x2-x+3,当x=0时,y=3,即点A的坐标为(0,3).
由题意,立柱EF左侧绳子所在抛物线的顶点为(2,1.8),所以可设其解析式为y=a(x-2)2+1.8,把x=0,y=3代入,得3=a(0-2)2+1.8,解得a=,所以y=(x-2)2+1.8.
当x=3时,y=×(3-2)2+1.8=2.1,所以立柱EF的长为2.1
m.
11.
解:(1)根据题意,该抛物线的解析式为y=-(x-6)2+4(或y=-x2+x+1).
(2)令y=0,得-(x-6)2+4=0,解得x1=4+6≈13,x2=-4+6<0(舍去),所以足球第一次落地点C距守门员13米.
(3)如图,足球第二次弹出后的距离为CD,根据题意知CD=EF(即相当于将抛物线AEMFC向下平移了2个单位),所以-(x-6)2+4=2,解得x1=6-2,x2=6+2,所以CD=x2-x1=4≈10,所以BD=13-6+10=17米,答:运动员乙要抢到足球第二个落地点D,他应再向前跑17米.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www。21cnjy。com)
人教版九年级数学上册课时作业
第二十二章 二次函数
22.3 实际问题与二次函数
第3课时 建立适当坐标系解决实际问题
1.
如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,则在线段AB上离中心M处5米的地方,桥的高度是( )
A.15米
B.14米
C.13米
D.12米
2.
某公园草坪的防护栏是由150段形状相同的抛物线组成的.如图,为了牢固起见,每段护栏需要间距0.4
m加设一根不锈钢的支柱,防护栏的最高点距底部0.5
m,则这条防护栏需要不锈钢支柱的总长度至少为( )
A.240
m
B.200
m
C.160
m
D.150
m
3.
小明学习了这节课后,课下竖直向上抛一个小球做实验,小球上升的高度h(m)与运动时间t(s)的函数关系式为h=at2+bt,图象如图所示.若小球在抛出后第2
s与第6
s时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3
s
B.第3.9
s
C.第4.5
s
D.第6.5
s
4.
位于中国贵州省内的射电望远镜(FAST)是目前世界上口径最大、精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点C到口径面AB的距离是100米.若按如图2建立平面直角坐标系,则抛物线的解析式是( )
A.y=x2-100
B.y=-x2-100
C.y=x2
D.y=-x2
5.
超市有一种果冻礼盒,内装两个上下倒置的果冻,果冻高为4
cm,底面是个直径为6
cm的圆,轴截面可以近似地看作一个抛物线.为了节省成本,包装应尽可能的小,这个包装盒的长AD(不计重合部分,两个果冻之间没有挤压)至少为( )
A.(6+3)cm
B.(6+2)cm
C.(6+2)cm
D.(6+3)cm
6.
一位运动员在距篮下4
m处跳起投篮,球运行的路线是抛物线.当球运行的水平距离为2.5
m时,达到最大高度3.5
m,然后准确落入篮圈.如图所示,已知篮圈中心到地面的距离为3.05
m,该运动员身高1.9
m.在这次跳投中,球在头顶上方0.25
m处出手,则球出手时,他跳离地面的高度是
.?
7.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状.身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点到地面的距离为
米.?
8.
图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86
m,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为
m.?
9.
如图,丁丁设计了一款杯子,杯子的上半部分是二次函数y=2x2+8的图象的一部分.若AB=4,DE=3,求杯子的高CE.
10.
如图1,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的平面直角坐标系,这条绳子可以用y=x2-x+3表示.
(1)求这条绳子的最低点到地面的距离;
(2)现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑(如图2),已知立柱EF到AB的距离为3
m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1
m,到地面的距离为1.8
m,求立柱EF的长.
11.
某校进行了一场足球比赛,比赛场上守门员小王在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的解析式.
(2)足球第一次落地点C距守门员多少米?(取4≈7)
(3)运动员乙要抢到足球第二个落地点D,他应再向前跑多少米?(取2≈5)
参
考
答
案
1.
A
2.
A
3.
B
4.
A
5.
A
6.
0.1
m
7.
0.5
8.
2.7
9.
解:由题意可得,点D的坐标为(0,8),∵AB=4,∴点B的横坐标为2,当x=2时,y=2×4+8=16,即B(2,16),∴CD=16-8=8,∴CE=CD+DE=8+3=11.
10.
解:(1)因为y=x2-x+3=(x-4)2+,所以抛物线的顶点坐标为(4,),则这条绳子的最低点到地面的距离为
m.
(2)对于y=x2-x+3,当x=0时,y=3,即点A的坐标为(0,3).
由题意,立柱EF左侧绳子所在抛物线的顶点为(2,1.8),所以可设其解析式为y=a(x-2)2+1.8,把x=0,y=3代入,得3=a(0-2)2+1.8,解得a=,所以y=(x-2)2+1.8.
当x=3时,y=×(3-2)2+1.8=2.1,所以立柱EF的长为2.1
m.
11.
解:(1)根据题意,该抛物线的解析式为y=-(x-6)2+4(或y=-x2+x+1).
(2)令y=0,得-(x-6)2+4=0,解得x1=4+6≈13,x2=-4+6<0(舍去),所以足球第一次落地点C距守门员13米.
(3)如图,足球第二次弹出后的距离为CD,根据题意知CD=EF(即相当于将抛物线AEMFC向下平移了2个单位),所以-(x-6)2+4=2,解得x1=6-2,x2=6+2,所以CD=x2-x1=4≈10,所以BD=13-6+10=17米,答:运动员乙要抢到足球第二个落地点D,他应再向前跑17米.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www。21cnjy。com)
同课章节目录
