七年级数学三角形的外角
图片预览



文档简介
(共27张PPT)
用牛皮筋拉成一个五角星,你也许也玩过这个游戏吧?
A
B
C
D
E
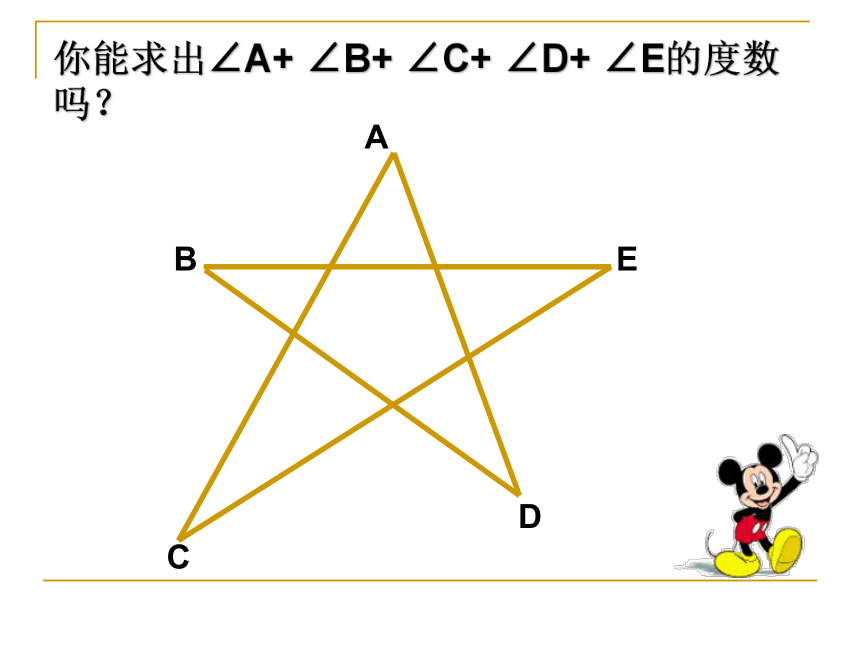
你能求出∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数吗?
A
B
C
E
A
B
C
1
E
1
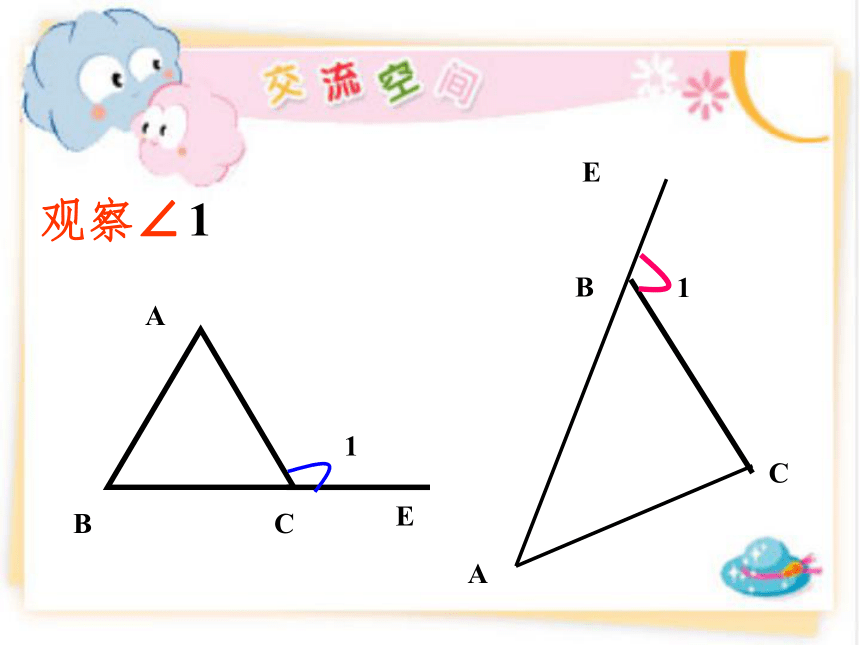
观察∠
1
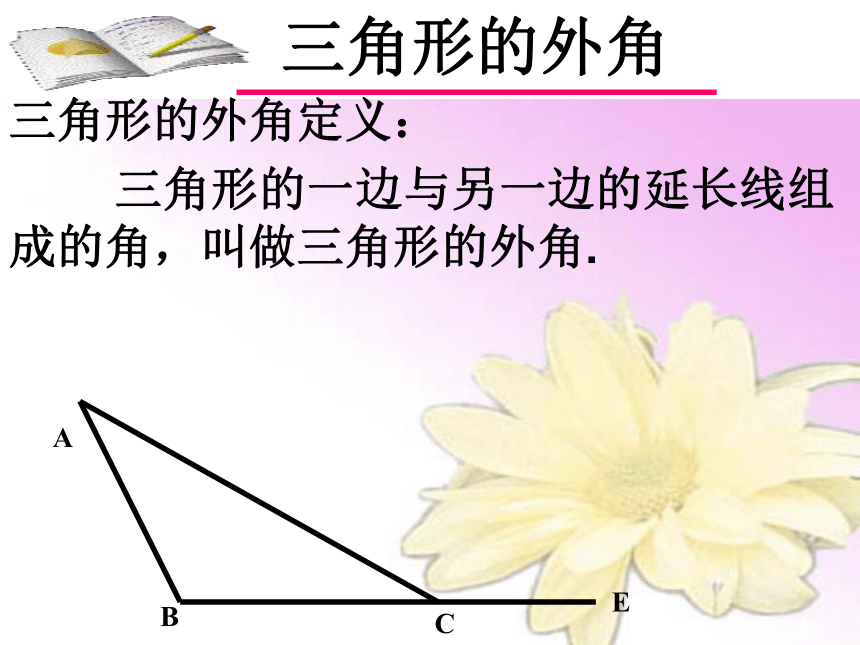
三角形的外角定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
A
B
C
E
三角形的外角
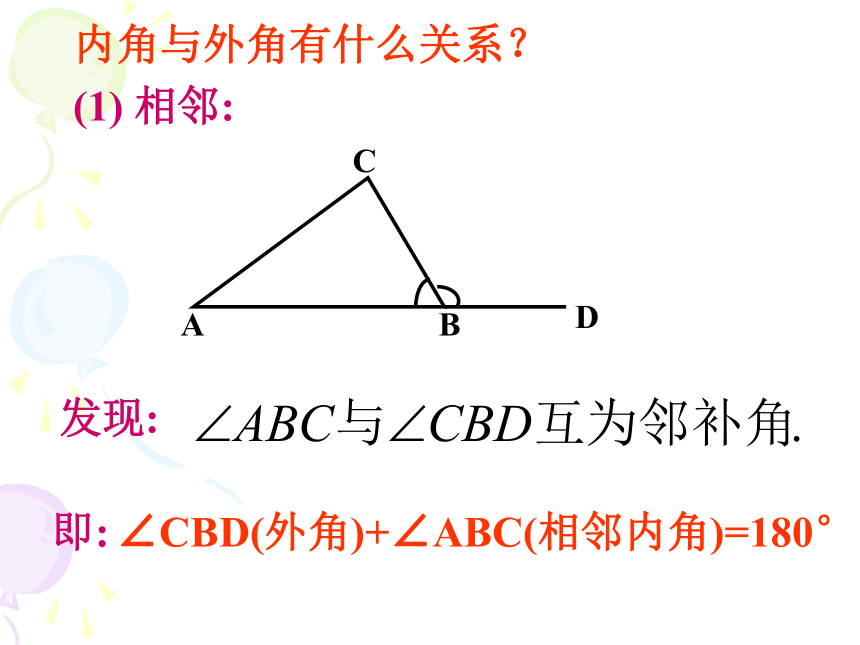
内角与外角有什么关系?
(1) 相邻:
C
A
B
D
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
下面探索三角形外角与不相邻内角间关系。
动手操作
(1)拿出准备好的纸板,画出其中的一个内角和与之相邻的一个外角。
(2)剪下这个三角形与外角,撕下两个不相邻的内角。
(3)把这两个不相邻的内角覆盖在这个外角的上面,使它们的顶点重合在一起,并把这两个内角不重叠地拼接成这两个角的和。
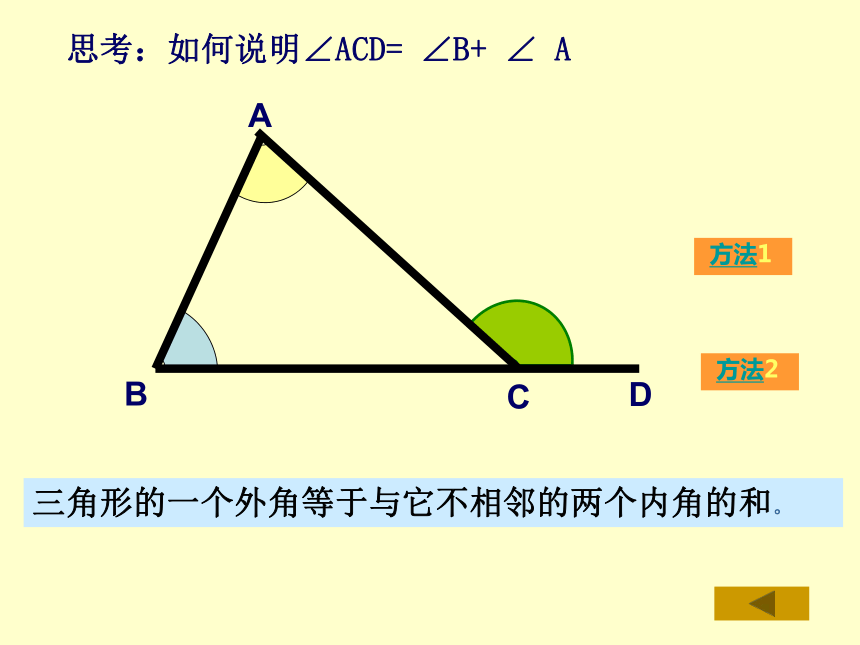
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
方法1
方法2
三角形的一个外角等于与它不相邻的两个内角的和。
D
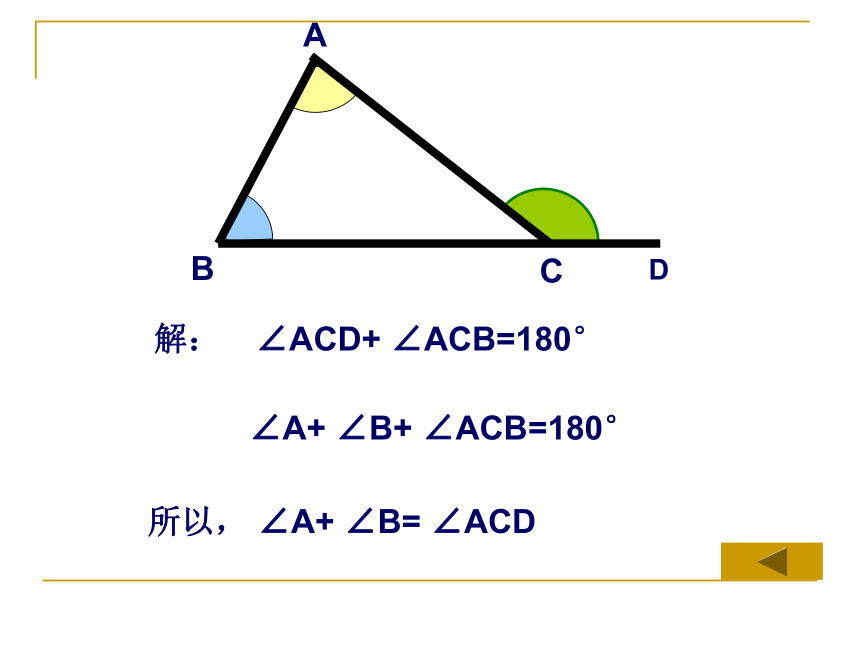
∠ACD+ ∠ACB=180°
∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
D
解:过C作CE平行于AB
A
B
C
1
2
∠1= ∠B
∠2= ∠A
∠1+ ∠2= ∠A+ ∠B
即∠ACD= ∠A+ ∠B
E
三角形的一个外角与三角形三个内角之间有何关系?
A
B
C
D
三角形的一个外角等于与它不相邻的两个内角的和。
三角形的一个外角与任何一个与它不相邻的内角之间又有什么关系呢?
三角形的外角大于任何一个与它不相邻的内角。
∠ACD> ∠ B
∠ACD= ∠ A+ ∠ B
∠ ACD+ ∠ ACB=180°
∠ACD> ∠ A
1、∠1,∠2,∠3各是哪个三角形的外角
2、 ∠1 ,∠3和∠A哪个大 为什么
A
B
C
D
E
1
2
3
例1
求下列各图中∠1的度数.
2
1
60°
55°
练习:求各图中∠1的度数
100 o
60 o
1
2、如果一个三角形一个外角等于和它相邻的内角的1/3,另一个内角是15°,那么第三个内角是多少度
3、已知三角形ABC三个内角之比是2:3:4,则该三角形的三个外角之比为----------
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的一个外角等于两个内角的和。( )
3、三角形的一个外角等于与它不相邻的两个内角的和。( )
4、三角形的一个外角大于任何一个内角。( )
5、三角形的一个内角小于任何一个与它不相邻的外角。( )
如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?
A
B
C
D
E
F
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
你认识外角吗
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
实际应用
解:∵∠1是△BDF的一个外角(外角的意义),
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
∴ ∠1=∠B+∠D(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和定理).
又∵ ∠2是△EHC的一个外角(外角的意义),
A
B
C
D
E
F
1
H
2
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
2、三角形的一个外角的性质
(3)三角形的一个外角大于任何一个与它不相邻的内角。
1、三角形的内角和180°
三角形内角和外角的性质
(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
(C组) P76 T5.6.8
若这些题感觉还不“过瘾”你可选做下列题目
作业(A\B)(备选)
1、如果三角形的一个外角与它不相邻的两个内角的和为180°,那么这个外角等于( )
2、 ∠1, ∠2, ∠3为ΔABC的外角,
若∠1:∠2:∠3=2:3:4,则
∠ABC等于( )
3、求下列图中各标出角的度数。
92 o
60 o
1
1
55°
60°
2
A
B
C
1
2
3
1
2
45°
35°
32°
40o
D
B
C
A
思考:如图D是ΔABC中AC边上一点,∠C=∠DBC,
(2)若∠A= ∠BDA, ∠ABD=40°
求∠C度数。
A组
A
B
C
D
E
若∠C=30°,求∠A+ ∠B+ ∠D+ ∠E的值
用牛皮筋拉成一个五角星,你也许也玩过这个游戏吧?
A
B
C
D
E
你能求出∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数吗?
A
B
C
E
A
B
C
1
E
1
观察∠
1
三角形的外角定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
A
B
C
E
三角形的外角
内角与外角有什么关系?
(1) 相邻:
C
A
B
D
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
下面探索三角形外角与不相邻内角间关系。
动手操作
(1)拿出准备好的纸板,画出其中的一个内角和与之相邻的一个外角。
(2)剪下这个三角形与外角,撕下两个不相邻的内角。
(3)把这两个不相邻的内角覆盖在这个外角的上面,使它们的顶点重合在一起,并把这两个内角不重叠地拼接成这两个角的和。
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
方法1
方法2
三角形的一个外角等于与它不相邻的两个内角的和。
D
∠ACD+ ∠ACB=180°
∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
D
解:过C作CE平行于AB
A
B
C
1
2
∠1= ∠B
∠2= ∠A
∠1+ ∠2= ∠A+ ∠B
即∠ACD= ∠A+ ∠B
E
三角形的一个外角与三角形三个内角之间有何关系?
A
B
C
D
三角形的一个外角等于与它不相邻的两个内角的和。
三角形的一个外角与任何一个与它不相邻的内角之间又有什么关系呢?
三角形的外角大于任何一个与它不相邻的内角。
∠ACD> ∠ B
∠ACD= ∠ A+ ∠ B
∠ ACD+ ∠ ACB=180°
∠ACD> ∠ A
1、∠1,∠2,∠3各是哪个三角形的外角
2、 ∠1 ,∠3和∠A哪个大 为什么
A
B
C
D
E
1
2
3
例1
求下列各图中∠1的度数.
2
1
60°
55°
练习:求各图中∠1的度数
100 o
60 o
1
2、如果一个三角形一个外角等于和它相邻的内角的1/3,另一个内角是15°,那么第三个内角是多少度
3、已知三角形ABC三个内角之比是2:3:4,则该三角形的三个外角之比为----------
判断题:
1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的一个外角等于两个内角的和。( )
3、三角形的一个外角等于与它不相邻的两个内角的和。( )
4、三角形的一个外角大于任何一个内角。( )
5、三角形的一个内角小于任何一个与它不相邻的外角。( )
如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?
A
B
C
D
E
F
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
你认识外角吗
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
实际应用
解:∵∠1是△BDF的一个外角(外角的意义),
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
∴ ∠1=∠B+∠D(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和定理).
又∵ ∠2是△EHC的一个外角(外角的意义),
A
B
C
D
E
F
1
H
2
∴ ∠A+∠B+∠C+∠D+∠E =180°(等式性质).
2、三角形的一个外角的性质
(3)三角形的一个外角大于任何一个与它不相邻的内角。
1、三角形的内角和180°
三角形内角和外角的性质
(1)三角形的一个外角与它相邻内角的关系是互为邻补角。
(2)三角形的一个外角等于与它不相邻的两个内角的和。
(C组) P76 T5.6.8
若这些题感觉还不“过瘾”你可选做下列题目
作业(A\B)(备选)
1、如果三角形的一个外角与它不相邻的两个内角的和为180°,那么这个外角等于( )
2、 ∠1, ∠2, ∠3为ΔABC的外角,
若∠1:∠2:∠3=2:3:4,则
∠ABC等于( )
3、求下列图中各标出角的度数。
92 o
60 o
1
1
55°
60°
2
A
B
C
1
2
3
1
2
45°
35°
32°
40o
D
B
C
A
思考:如图D是ΔABC中AC边上一点,∠C=∠DBC,
(2)若∠A= ∠BDA, ∠ABD=40°
求∠C度数。
A组
A
B
C
D
E
若∠C=30°,求∠A+ ∠B+ ∠D+ ∠E的值
