七年级数学三角形的外角和
图片预览

文档简介
(共24张PPT)
内
课题 : 三角形的外角和
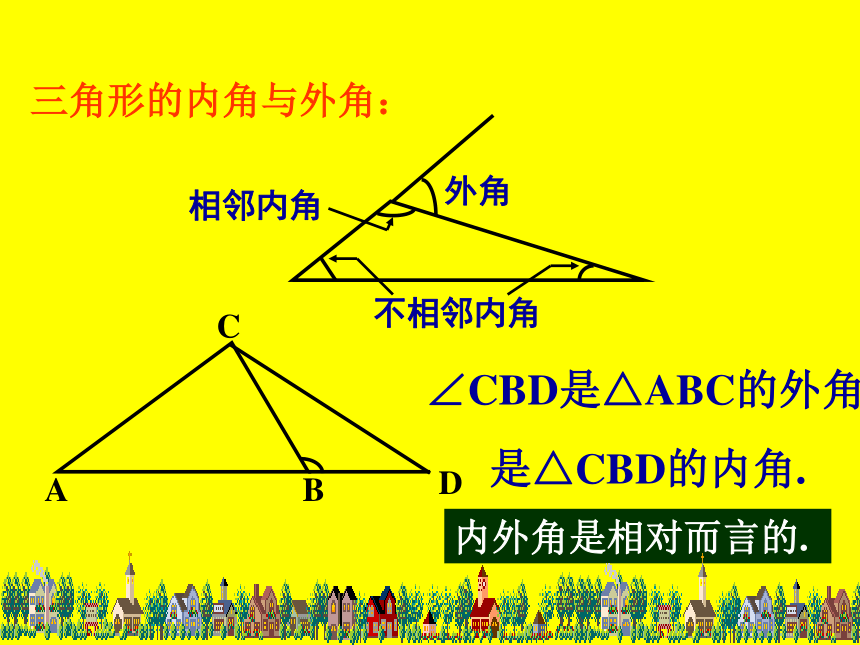
三角形的内角与外角:
C
A
B
D
内外角是相对而言的.
外角
相邻内角
不相邻内角
∠CBD是△ABC的外角.
是△CBD的内角.
A
B
C
D
E
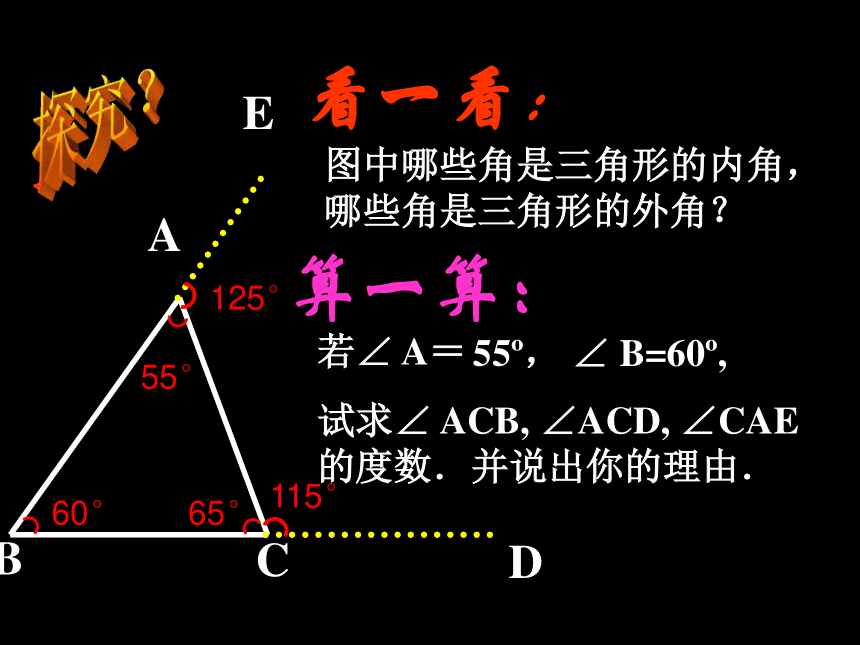
看一看:
算一算:
若∠ A=
55 , ∠ B=60 ,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
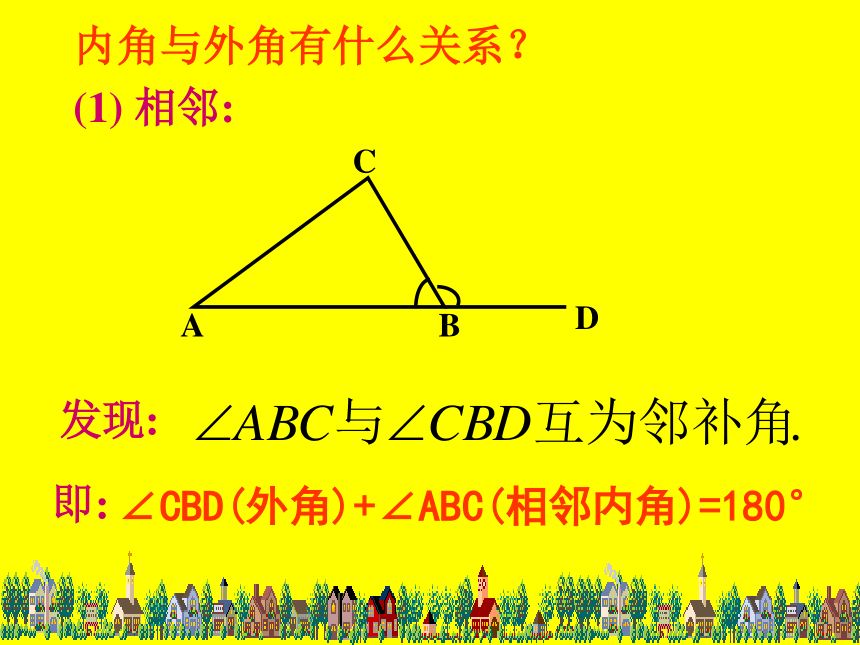
内角与外角有什么关系?
(1) 相邻:
C
A
B
D
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
演示
C
A
B
D
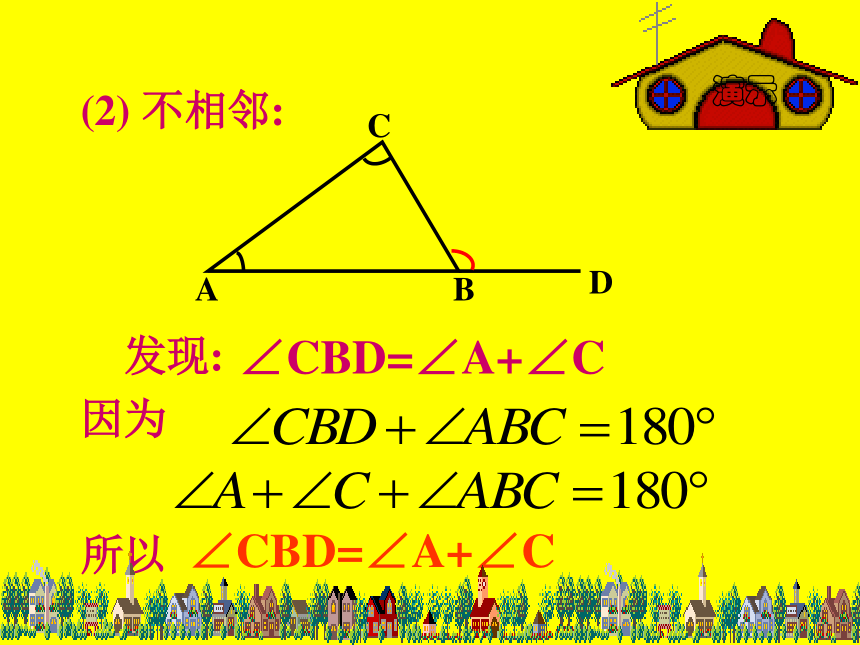
(2) 不相邻:
因为
所以
∠CBD=∠A+∠C
发现:
∠CBD=∠A+∠C
C
A
B
D
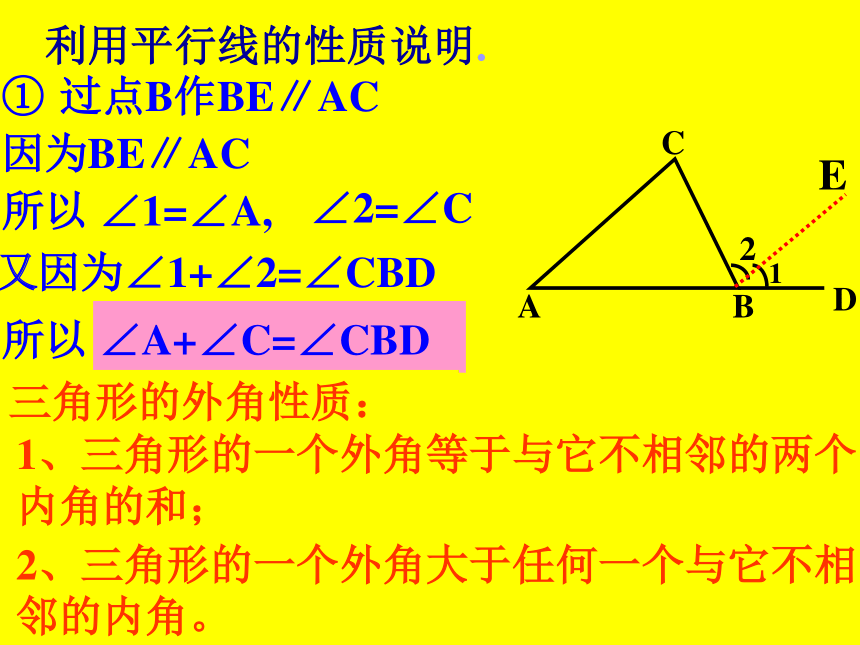
利用平行线的性质说明.
过点B作BE∥AC
①
因为BE∥AC
所以 ∠1=∠A,
1
2
E
又因为∠1+∠2=∠CBD
所以 ∠A+∠C=∠CBD
C
A
B
D
E
②
过点A作AE BC
C
A
B
D
E
③
过点C作CE AB
三角形的外角性质:
1、三角形的一个外角等于与它不相邻的两个内角的和;
2、三角形的一个外角大于任何一个与它不相邻的内角。
∠2=∠C
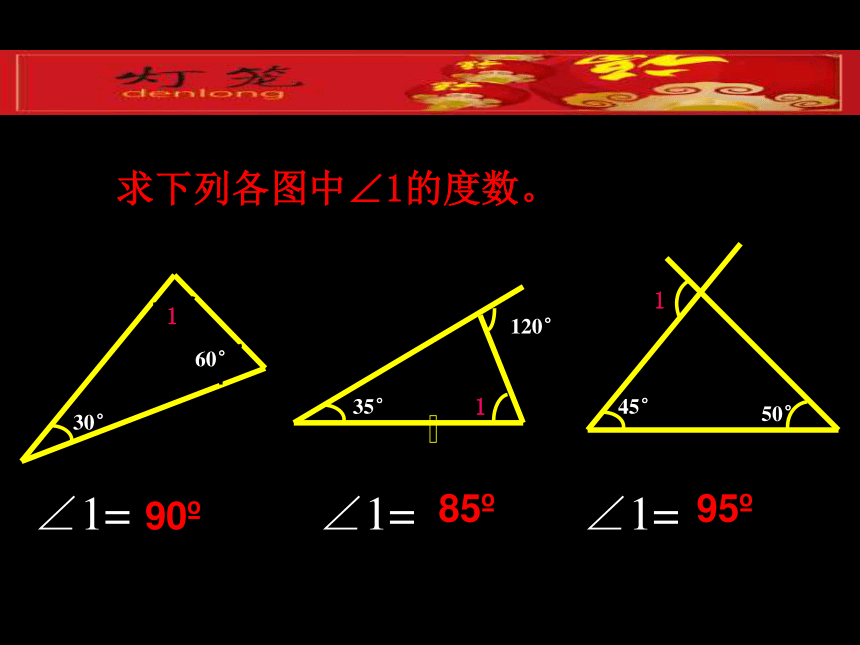
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90
85
95
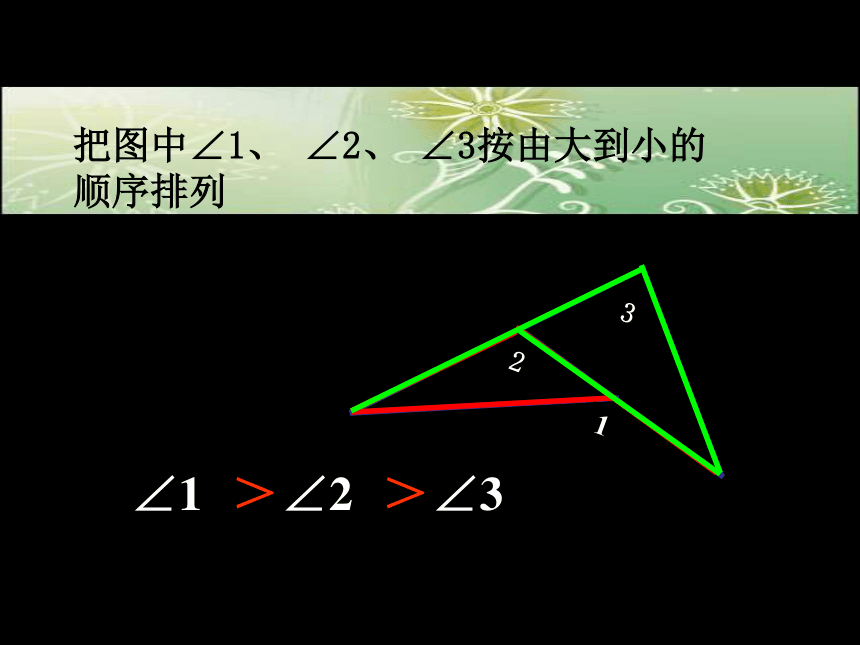
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
>
>
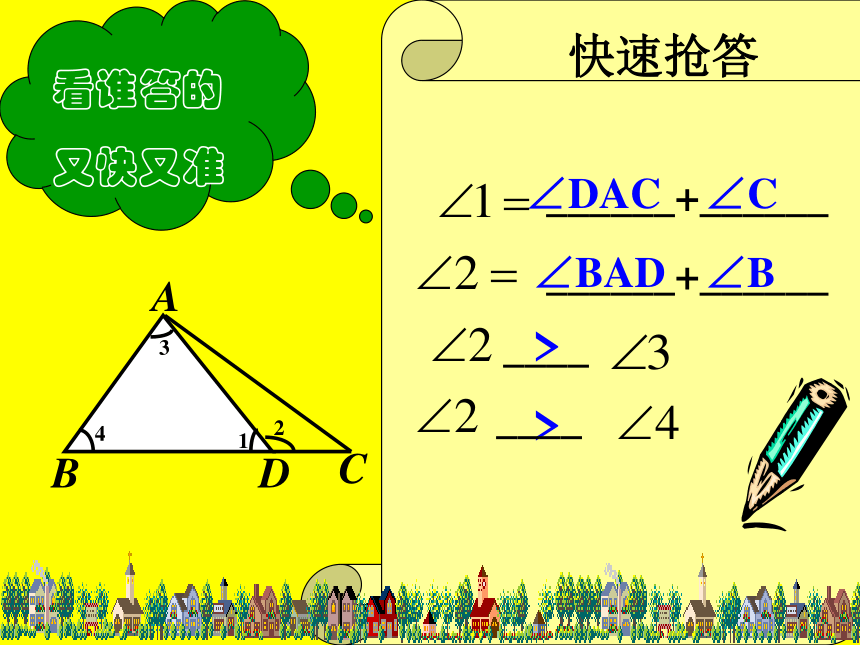
∠DAC
∠C
∠BAD
∠B
______+______
______+______
____
____
A
B
D
C
1
2
4
3
快速抢答
看谁答的
又快又准
A
B
C
1
2
3
方法1
方法2
三角形的外角和等于360°
∠1+∠2 +∠3 =
从哪些途径探究这个结果
议一议
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
解:过A作AD平行于BC
∴ ∠3= ∠4
B
C
1
2
3
4
A
∴ ∠2= ∠BAD
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
两直线平行,同位角相等
D
例1
∠B=∠BAD,∠ADC=80°, ∠ BAC=70°.求:⑴∠B的度数;⑵ ∠C的度数。
A
B
C
D
如图,D是△ABC的BC边上一点,
解:
⑴
因为∠ADC是△ABD的外角,
∠ADC=∠B+∠BAD=80°
又 ∠B=∠BAD
所以∠B=80° =40°
80°
70°
所以
⑵
在△ABC中,
所以∠C= 180°- ∠B-∠BAC
=70°
因为∠B+∠BAC+∠C=180°
=180°-40°-70°
例2
如图,一根电线杆立于河水中,
两岸各用一根铁丝将其固定,现测得铁丝分别与两岸地面成110°和120°的角.求两铁丝所成的角.
A
解:
因为∠ABC+∠ABD=180°
所以∠ABC =70°
因为∠ACE是△ABC的外角
所以∠ACE=∠ABC+∠BAC
=120°-70°
=50°
答:两铁丝所成的角为50°
又因为∠ABD=110°
所以∠BAC=∠ACE-∠ABC
B
D
C
E
110°
120°
1、如图,已知∠AEC=110°,求∠A+∠B+∠C+∠D的度数。
A
B
C
D
E
练习
解:因为∠AEC是△ABE的外角,所以
∠AEC=∠A+∠B=110°
∠AEC=∠C+∠D=110°
所以∠A+∠B+∠C+∠D=220°
因为∠AEC是△CDE的外角,所以
A
2、如图在五角星ABCDE中,求∠A+∠B+∠C+∠D+∠E的度数。
B
C
D
E
F
G
所以∠A+∠D+∠B+∠E+∠C=180°
所以∠2= ∠B+∠E.
解:
如图所示
因为∠1是△ BEG 的外角,
所以∠1= ∠A+∠D.
因为∠2是△ AFG的外角,
在△CFG中,
∠1+∠2+∠C=180°
即
∠A+∠B+∠C+∠D+∠E=180°
1
2
小结:
2、三角形的一个外角等于和它不相邻的两个内角的和;
1、三角形的外角与相邻内角互补;
3、三角形的一个外角大于任何一个和它不相邻的内角;
4、三角形的外角和等于360°.
㈠结论:
㈡思想与方法:
1、割补的思想;
2、利用平行性质说明;
3、运用三角形内、外角性质及三角形内、外角和计算角度.
“行家”看“门道”
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∴ AD ∥BC(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∵ AD平分 ∠EAC(已知).
∴∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
一题多解思维灵活
A
C
D
B
E
·
·
∠B=∠C (已知),
∴∠B= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAE= ∠EAC(角平分线的定义).
∴∠DAE=∠B(等量代换).
∴ AD∥BC(同位角相等,两直线平行).
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.
A
C
D
B
E
·
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∠DAC=∠C (已证),
∵ ∠BAC+∠B+∠C =1800 (三角形内角和定理).
∴ ∠BAC+∠B+∠DAC =1800 (等量代换).
∴ AD∥BC(同旁内角互补,两直线平行).
这里是运用了定理“同旁内角互补,两直线平行”得到了证实.
证明:由证法1可得:
·
一题多解思维灵活
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.
作业
1、 配套作业本。
2、 小作文
通过本节课的学习,谈谈从中得到的
收获与启示,明确今后努力的方向
把眼光盯住内角,只能看到:
三角形内角和是180度;
四边形内角和是360度;
五边形内角和是540度; ……
n边形内角和是(n—2)X180度。
这就找到了一个计算内角和的公式。公式里
出现了边数n。
如果看外角呢
三角形的外角和是360度;
四边形的外角和是360度;
五边形的外角和是360度; ……
任意n边形外角和都是360度。
这就把多种情形用一个十分简单的结论概括起来了。用一个与n无关的常数代替了与n有关的公式,找到了更一般的规律。
内
课题 : 三角形的外角和
三角形的内角与外角:
C
A
B
D
内外角是相对而言的.
外角
相邻内角
不相邻内角
∠CBD是△ABC的外角.
是△CBD的内角.
A
B
C
D
E
看一看:
算一算:
若∠ A=
55 , ∠ B=60 ,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
内角与外角有什么关系?
(1) 相邻:
C
A
B
D
发现:
即:
∠CBD(外角)+∠ABC(相邻内角)=180°
演示
C
A
B
D
(2) 不相邻:
因为
所以
∠CBD=∠A+∠C
发现:
∠CBD=∠A+∠C
C
A
B
D
利用平行线的性质说明.
过点B作BE∥AC
①
因为BE∥AC
所以 ∠1=∠A,
1
2
E
又因为∠1+∠2=∠CBD
所以 ∠A+∠C=∠CBD
C
A
B
D
E
②
过点A作AE BC
C
A
B
D
E
③
过点C作CE AB
三角形的外角性质:
1、三角形的一个外角等于与它不相邻的两个内角的和;
2、三角形的一个外角大于任何一个与它不相邻的内角。
∠2=∠C
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90
85
95
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
>
>
∠DAC
∠C
∠BAD
∠B
______+______
______+______
____
____
A
B
D
C
1
2
4
3
快速抢答
看谁答的
又快又准
A
B
C
1
2
3
方法1
方法2
三角形的外角和等于360°
∠1+∠2 +∠3 =
从哪些途径探究这个结果
议一议
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
解:过A作AD平行于BC
∴ ∠3= ∠4
B
C
1
2
3
4
A
∴ ∠2= ∠BAD
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
两直线平行,同位角相等
D
例1
∠B=∠BAD,∠ADC=80°, ∠ BAC=70°.求:⑴∠B的度数;⑵ ∠C的度数。
A
B
C
D
如图,D是△ABC的BC边上一点,
解:
⑴
因为∠ADC是△ABD的外角,
∠ADC=∠B+∠BAD=80°
又 ∠B=∠BAD
所以∠B=80° =40°
80°
70°
所以
⑵
在△ABC中,
所以∠C= 180°- ∠B-∠BAC
=70°
因为∠B+∠BAC+∠C=180°
=180°-40°-70°
例2
如图,一根电线杆立于河水中,
两岸各用一根铁丝将其固定,现测得铁丝分别与两岸地面成110°和120°的角.求两铁丝所成的角.
A
解:
因为∠ABC+∠ABD=180°
所以∠ABC =70°
因为∠ACE是△ABC的外角
所以∠ACE=∠ABC+∠BAC
=120°-70°
=50°
答:两铁丝所成的角为50°
又因为∠ABD=110°
所以∠BAC=∠ACE-∠ABC
B
D
C
E
110°
120°
1、如图,已知∠AEC=110°,求∠A+∠B+∠C+∠D的度数。
A
B
C
D
E
练习
解:因为∠AEC是△ABE的外角,所以
∠AEC=∠A+∠B=110°
∠AEC=∠C+∠D=110°
所以∠A+∠B+∠C+∠D=220°
因为∠AEC是△CDE的外角,所以
A
2、如图在五角星ABCDE中,求∠A+∠B+∠C+∠D+∠E的度数。
B
C
D
E
F
G
所以∠A+∠D+∠B+∠E+∠C=180°
所以∠2= ∠B+∠E.
解:
如图所示
因为∠1是△ BEG 的外角,
所以∠1= ∠A+∠D.
因为∠2是△ AFG的外角,
在△CFG中,
∠1+∠2+∠C=180°
即
∠A+∠B+∠C+∠D+∠E=180°
1
2
小结:
2、三角形的一个外角等于和它不相邻的两个内角的和;
1、三角形的外角与相邻内角互补;
3、三角形的一个外角大于任何一个和它不相邻的内角;
4、三角形的外角和等于360°.
㈠结论:
㈡思想与方法:
1、割补的思想;
2、利用平行性质说明;
3、运用三角形内、外角性质及三角形内、外角和计算角度.
“行家”看“门道”
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
∴ AD ∥BC(内错角相等,两直线平行).
∠B=∠C (已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∵ AD平分 ∠EAC(已知).
∴∠C= ∠EAC(等式性质).
∴∠DAC= ∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
一题多解思维灵活
A
C
D
B
E
·
·
∠B=∠C (已知),
∴∠B= ∠EAC(等式性质).
∵ AD平分 ∠EAC(已知).
∴∠DAE= ∠EAC(角平分线的定义).
∴∠DAE=∠B(等量代换).
∴ AD∥BC(同位角相等,两直线平行).
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.
A
C
D
B
E
·
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∠DAC=∠C (已证),
∵ ∠BAC+∠B+∠C =1800 (三角形内角和定理).
∴ ∠BAC+∠B+∠DAC =1800 (等量代换).
∴ AD∥BC(同旁内角互补,两直线平行).
这里是运用了定理“同旁内角互补,两直线平行”得到了证实.
证明:由证法1可得:
·
一题多解思维灵活
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.
作业
1、 配套作业本。
2、 小作文
通过本节课的学习,谈谈从中得到的
收获与启示,明确今后努力的方向
把眼光盯住内角,只能看到:
三角形内角和是180度;
四边形内角和是360度;
五边形内角和是540度; ……
n边形内角和是(n—2)X180度。
这就找到了一个计算内角和的公式。公式里
出现了边数n。
如果看外角呢
三角形的外角和是360度;
四边形的外角和是360度;
五边形的外角和是360度; ……
任意n边形外角和都是360度。
这就把多种情形用一个十分简单的结论概括起来了。用一个与n无关的常数代替了与n有关的公式,找到了更一般的规律。
