数学人教A版(2019)必修一2.1.2《指数函数及其性质》(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修一2.1.2《指数函数及其性质》(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 652.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 19:38:34 | ||
图片预览








文档简介
(共22张PPT)
第二章
基本初等函数(Ⅰ)
§2.1.2
指数函数及其性质
第一课时
指数函数的概念与图象
学习目标
1.了解指数函数模型的实际背景,理解指数函数的概念,
掌握指数函数的图象.
2.初步学会运用指数函数解决问题.
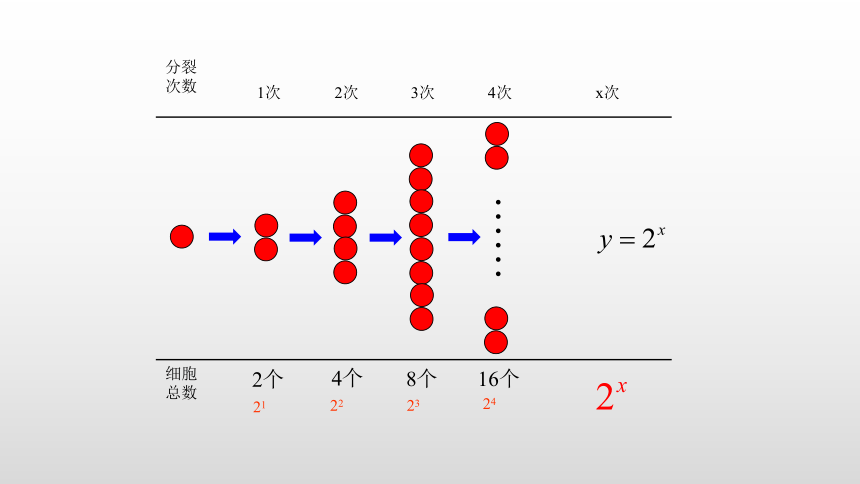
问题1、某种细胞分裂时,由1个分裂成
2个,2个分裂成4个,1个这样的细胞分
裂x次后,得到的细胞个数y与x的函数
关系式是什么?
问题引入
分裂
次数
细胞
总数
1次
2次
3次
4次
x次
……
21
22
23
24
分析:
设该物质经过x年后的剩留量为y
若设该物质原有量为1
则经过一年剩留量为:
经过二年剩留量为:
经过三年剩留量为:
……
即经过x年后的剩留量是
问题2
一种放射性物质不断衰减为其它物质,每经过一年剩留量约为原来的84%,则这种物质经过x年后的剩留量是多少?
设疑自探
思考:这两个解析式有什么共同特征?
分析:
对于这两个解析式都具有
的形式,其中自变量x是指数,底数a是一个大于0且不等于1的常数。
指数函数的概念
注意
:
(1)ax为一个整体,前面系数为1;
(2)底数
a>0且
a≠1
;
(3)自变量x在幂指数的位置且为单个x;
思考:为什么概念中明确规定a>0,且a≠1?
?
(3)如果a=1,那么y=1x=1是常量,对此就没有研究的必要.
规定底数a>0且a≠1的理由
(1)如果a=0,则当x>0时,ax恒为0;当x<0时,ax无意义.
(2)如果a<0,比如y=(-2)x,这时对于x=,,,,…在实数范围内函数值不存在.
学以致用:题型一:指数函数的概念
【例1】下列函数中,哪些是指数函数?
(1)y=4x;(2)y=x4;(3)y=-4x;(4)y=(-4)x;
(5)y=πx;(6)y=4x2;(7)y=42x;(8)y=(2a1)x(a>,a≠1),x∈R
[解析]
(1)、(5)、(7)、(8)为指数函数;
(2)中底数x不是常数,而4不是自变量;
(3)是-1与指数函数4x的乘积;
(4)中底数-4<0,∴不是指数函数;
(6)是二次函数,它们都不符合指数函数的定义.
变式训练:
【变式1】(1)函数y=(2a2-3a+2)·ax是指数函数,则a的值________.
(2)指数函数f(x)的图象过点(-3,),则f(2)=________.
[解析]
(1)y=(2a2-3a+2)·ax是指数函数,则有,∴a=.
[答案] (1)
(2)4
∴f(2)=22=4.
∴f(x)=2x,
∵f(x)的图象过点(-3,),
∴a-3=,a3=8,故a=2,
(2)设f(x)=ax(a>0,且a≠1).
解疑合探
探究点2
指数函数的图象和性质
画出,的图像,并分析函数图象有哪些特点?
思考:描点法画函数图象有哪些步骤?
列表、
描点、
连线
提示:
小组合探
列表:
x
-2
-1
0
1
2
1
1
1
2
4
4
2
3
1
9
3
9
0
1
1
描点、连线
a越大,曲线约往y轴靠近,且都过定点(0,1)
0
1
1
0
1
1
0
1
0
1
y=ax
(0y=ax
(a>1)
指数函数性质一览表
函数
y=ax
(a>1)
y=ax
(0图
象
定义域
R
值
域
性质
(0,1
)
单调性
在R上是增函数
在R上是减函数
若x>0,
则y>1
若x<0,
则0若x<0,
则y>1
若x>0,
则0定
点
没有奇偶性
没有最值
归纳
质疑再探
比较下列各组数的大小:
①
②
③
④
解:①
1.72.5、1.73可以看作函数y=1.7x的两个函数值
∵1.7>1
∴
y=1.7x在R上是增函数
又∵2.5<3
∴
1.72.5
<
1.73
在a1=0.8,a2=0.6下的函数值
解:②
可以看做是函数
∵
a1<0
,
a2<0
∴函数
为减函数
又∵
,
x=1.3>0
∴0.81.3>0.61.3
解:③
∵1.70.3>1,而0.93.1<1
解:④
②异底同指:构造函数法(多个),利用函数图象在y轴左右两侧的特点。
比较指数幂大小的方法:
①同底异指:构造函数法(一个),
利用函数的单调性,若底数是参变量要注意分类讨论。
③异底异指:寻求中间量
运用拓展
1.下列各函数中,是指数函数的是
( )
A.y=(-3)x
B.y=-3x
C.y=3x-1
D.y=3-x
答案: D
y=3-x=()x为指数函数,其余均不是.
[解析]
2.y=()x的图象可能是(
)
答案: A
x
y
O
A
x
y
B
x
y
C
x
y
D
3.当a>0且a≠1时,函数f(x)=ax-2-3必过定点________.
答案: (2,-2)
所以当x=2时,y=-2,f(x)过点(2,-2).
[解析]:
当a>0且a≠1时,总有a0=1,
(-1/2,0)
归纳小结
1.指数函数的概念:形如y=ax(a>0,且a≠1)的函数称为指数函数.
指数函数特征:
(1)底数a为大于0且不等于1的常数,不含有自变量x;
2.指数函数的图象和简单性质,指数函数定义域为R,值域为(0,+∞),当
a>1时函数单调递增,当0(3)ax的系数是1.
(2)指数位置是自变量x,且x的系数是1;
布置作业
课本P59:习题
2.1:5.
第二章
基本初等函数(Ⅰ)
§2.1.2
指数函数及其性质
第一课时
指数函数的概念与图象
学习目标
1.了解指数函数模型的实际背景,理解指数函数的概念,
掌握指数函数的图象.
2.初步学会运用指数函数解决问题.
问题1、某种细胞分裂时,由1个分裂成
2个,2个分裂成4个,1个这样的细胞分
裂x次后,得到的细胞个数y与x的函数
关系式是什么?
问题引入
分裂
次数
细胞
总数
1次
2次
3次
4次
x次
……
21
22
23
24
分析:
设该物质经过x年后的剩留量为y
若设该物质原有量为1
则经过一年剩留量为:
经过二年剩留量为:
经过三年剩留量为:
……
即经过x年后的剩留量是
问题2
一种放射性物质不断衰减为其它物质,每经过一年剩留量约为原来的84%,则这种物质经过x年后的剩留量是多少?
设疑自探
思考:这两个解析式有什么共同特征?
分析:
对于这两个解析式都具有
的形式,其中自变量x是指数,底数a是一个大于0且不等于1的常数。
指数函数的概念
注意
:
(1)ax为一个整体,前面系数为1;
(2)底数
a>0且
a≠1
;
(3)自变量x在幂指数的位置且为单个x;
思考:为什么概念中明确规定a>0,且a≠1?
?
(3)如果a=1,那么y=1x=1是常量,对此就没有研究的必要.
规定底数a>0且a≠1的理由
(1)如果a=0,则当x>0时,ax恒为0;当x<0时,ax无意义.
(2)如果a<0,比如y=(-2)x,这时对于x=,,,,…在实数范围内函数值不存在.
学以致用:题型一:指数函数的概念
【例1】下列函数中,哪些是指数函数?
(1)y=4x;(2)y=x4;(3)y=-4x;(4)y=(-4)x;
(5)y=πx;(6)y=4x2;(7)y=42x;(8)y=(2a1)x(a>,a≠1),x∈R
[解析]
(1)、(5)、(7)、(8)为指数函数;
(2)中底数x不是常数,而4不是自变量;
(3)是-1与指数函数4x的乘积;
(4)中底数-4<0,∴不是指数函数;
(6)是二次函数,它们都不符合指数函数的定义.
变式训练:
【变式1】(1)函数y=(2a2-3a+2)·ax是指数函数,则a的值________.
(2)指数函数f(x)的图象过点(-3,),则f(2)=________.
[解析]
(1)y=(2a2-3a+2)·ax是指数函数,则有,∴a=.
[答案] (1)
(2)4
∴f(2)=22=4.
∴f(x)=2x,
∵f(x)的图象过点(-3,),
∴a-3=,a3=8,故a=2,
(2)设f(x)=ax(a>0,且a≠1).
解疑合探
探究点2
指数函数的图象和性质
画出,的图像,并分析函数图象有哪些特点?
思考:描点法画函数图象有哪些步骤?
列表、
描点、
连线
提示:
小组合探
列表:
x
-2
-1
0
1
2
1
1
1
2
4
4
2
3
1
9
3
9
0
1
1
描点、连线
a越大,曲线约往y轴靠近,且都过定点(0,1)
0
1
1
0
1
1
0
1
0
1
y=ax
(0
(a>1)
指数函数性质一览表
函数
y=ax
(a>1)
y=ax
(0
象
定义域
R
值
域
性质
(0,1
)
单调性
在R上是增函数
在R上是减函数
若x>0,
则y>1
若x<0,
则0
则y>1
若x>0,
则0
点
没有奇偶性
没有最值
归纳
质疑再探
比较下列各组数的大小:
①
②
③
④
解:①
1.72.5、1.73可以看作函数y=1.7x的两个函数值
∵1.7>1
∴
y=1.7x在R上是增函数
又∵2.5<3
∴
1.72.5
<
1.73
在a1=0.8,a2=0.6下的函数值
解:②
可以看做是函数
∵
a1<0
,
a2<0
∴函数
为减函数
又∵
,
x=1.3>0
∴0.81.3>0.61.3
解:③
∵1.70.3>1,而0.93.1<1
解:④
②异底同指:构造函数法(多个),利用函数图象在y轴左右两侧的特点。
比较指数幂大小的方法:
①同底异指:构造函数法(一个),
利用函数的单调性,若底数是参变量要注意分类讨论。
③异底异指:寻求中间量
运用拓展
1.下列各函数中,是指数函数的是
( )
A.y=(-3)x
B.y=-3x
C.y=3x-1
D.y=3-x
答案: D
y=3-x=()x为指数函数,其余均不是.
[解析]
2.y=()x的图象可能是(
)
答案: A
x
y
O
A
x
y
B
x
y
C
x
y
D
3.当a>0且a≠1时,函数f(x)=ax-2-3必过定点________.
答案: (2,-2)
所以当x=2时,y=-2,f(x)过点(2,-2).
[解析]:
当a>0且a≠1时,总有a0=1,
(-1/2,0)
归纳小结
1.指数函数的概念:形如y=ax(a>0,且a≠1)的函数称为指数函数.
指数函数特征:
(1)底数a为大于0且不等于1的常数,不含有自变量x;
2.指数函数的图象和简单性质,指数函数定义域为R,值域为(0,+∞),当
a>1时函数单调递增,当0
(2)指数位置是自变量x,且x的系数是1;
布置作业
课本P59:习题
2.1:5.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
