11.2.1三角形的内角和 课件(共20张PPT)
文档属性
| 名称 | 11.2.1三角形的内角和 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 10:49:27 | ||
图片预览



文档简介
(共22张PPT)
人教版
八年级上
三角形
—三角形的内角
目标:探索并证明三角形内角和定理,能运
用内角和定理解决简单问题
重点:探索并证明三角形内角和定理。
难点:三角形内角和定理的证明。
复习引入
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,二哥突然不高兴,发起脾气来,它指着大哥说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”大哥说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?”
二哥很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
情景导入
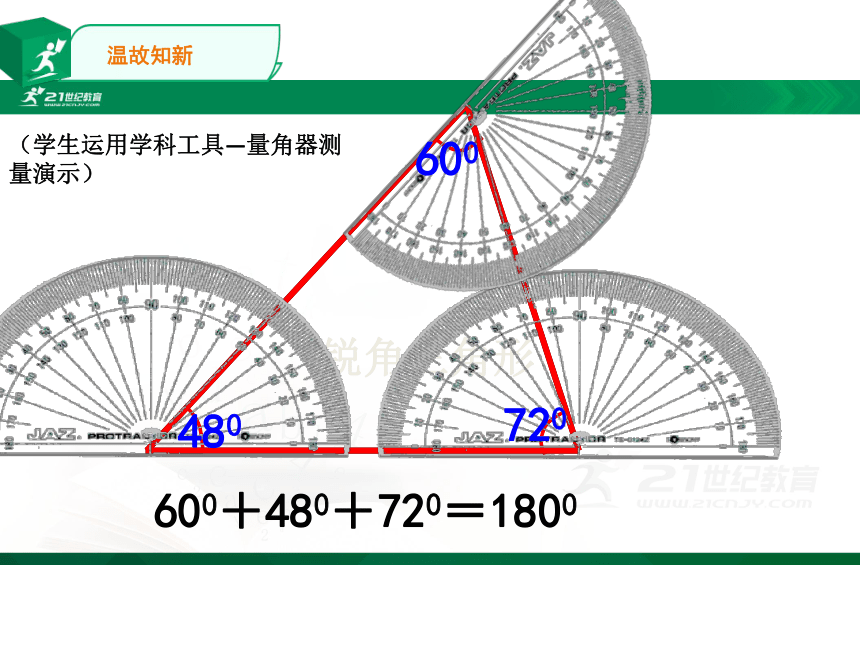
锐角三角形
480
720
600
600+480+720=1800
(学生运用学科工具—量角器测量演示)
温故知新
A
B
C
2
1
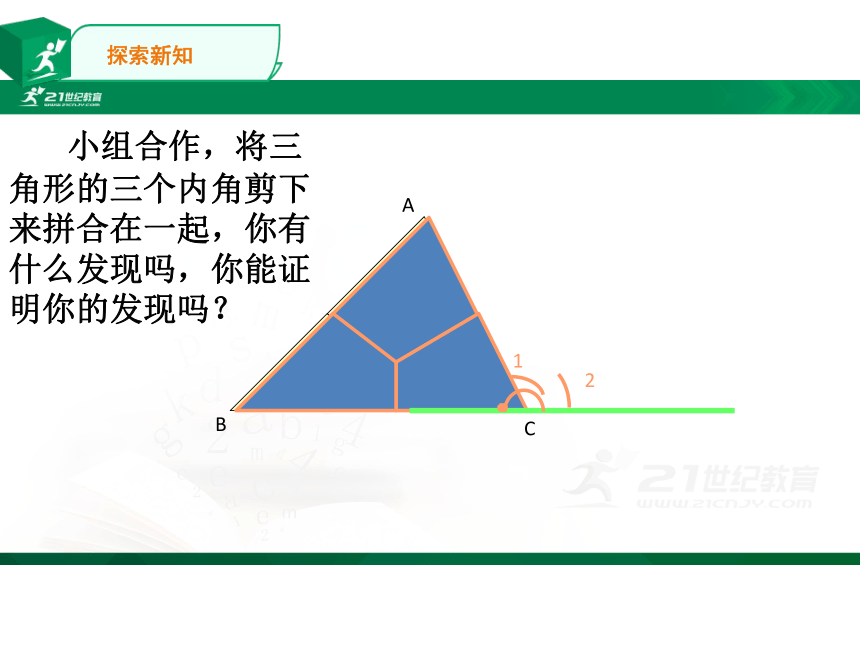
小组合作,将三角形的三个内角剪下来拼合在一起,你有什么发现吗,你能证明你的发现吗?
探索新知
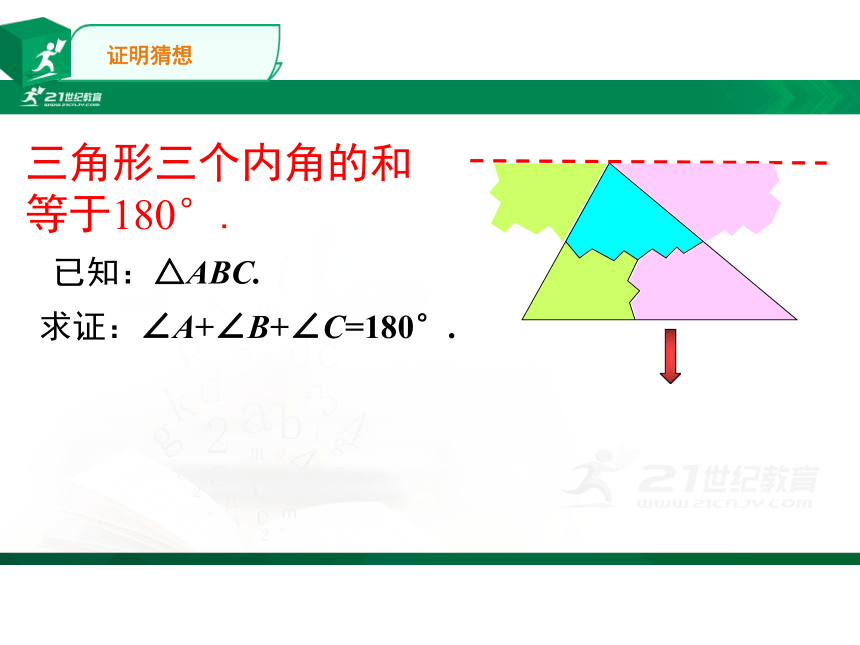
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证明猜想
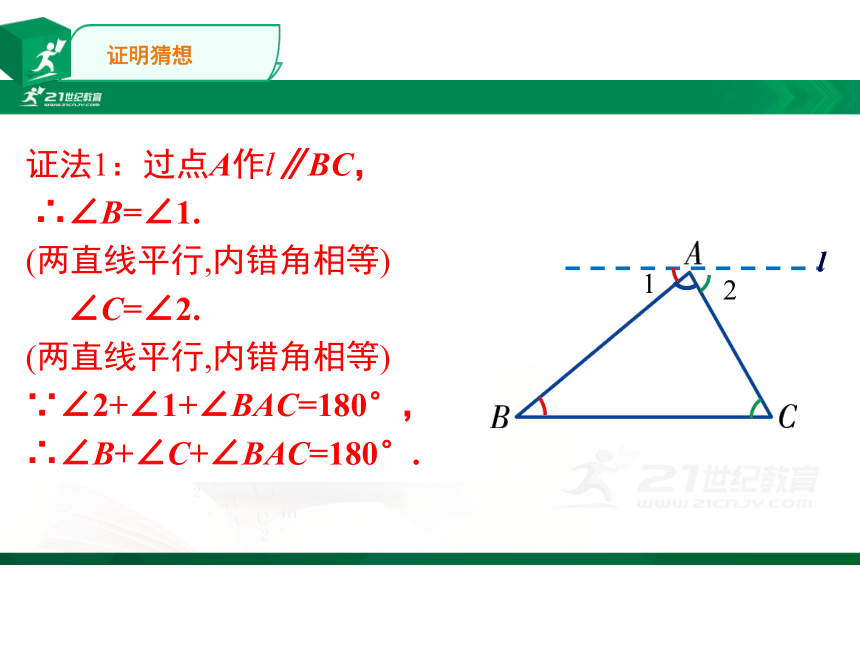
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
2
1
证明猜想
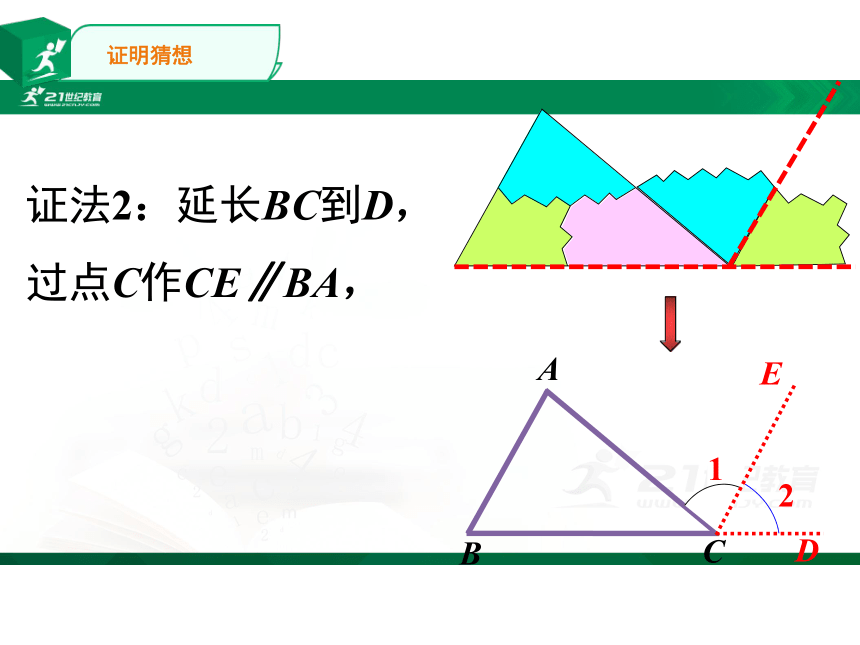
证法2:延长BC到D,过点C作CE∥BA,
C
B
A
E
D
1
2
证明猜想
C
B
A
E
D
F
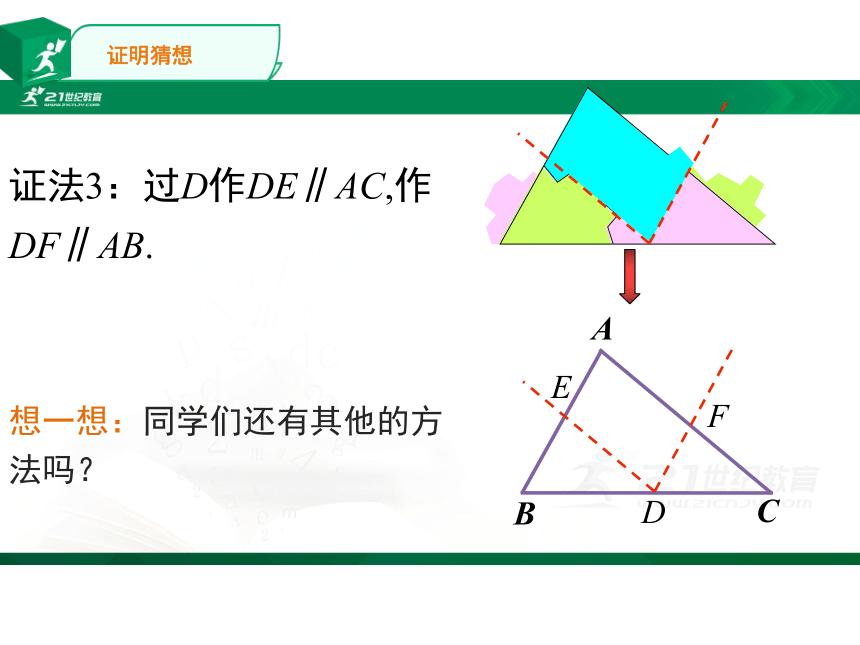
证法3:过D作DE∥AC,作DF∥AB.
想一想:同学们还有其他的方法吗?
证明猜想
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
归纳整理
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
B
G
C
2
4
A
3
E
D
F
H
1
试一试:同学们按照上图中的辅助线,给出证明步骤?
归纳整理
1.求出下列各图中的x值.
运用新知
如图,在△ABC中,
∠BAC=40
°,
∠B=75
°,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40
°,
AD是△ABC的角平分线,得
∠BAD=
∠BAC=20
°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°.
例题精讲
如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
跟踪训练
北
.
A
D
北
.
C
B
.
东
E
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
例题精讲
如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
D
E
跟踪训练
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一
样的玻璃,那么最省事的办法是
(
)
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
小试牛刀
2.如图,则∠1+∠2+∠3+∠4=___________
.
B
A
C
D
4
1
3
2
E
40°
(
小试牛刀
3.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
小试牛刀
小结回顾
1、运用平移角的原理证明三角形的内角和为180°。
2、证明命题的注意事项。
3、利用三角形的内角和解决方向角的有关问题。
2.在△ABC中,
∠A=
∠B+10°,
∠C=
∠A
+
10°,
则
∠A=
,
∠
B=
,∠
C=
.
(必做题)
1.课本第16页第4题(必做题)
作业布置
3.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.(选做题)
作业布置
人教版
八年级上
三角形
—三角形的内角
目标:探索并证明三角形内角和定理,能运
用内角和定理解决简单问题
重点:探索并证明三角形内角和定理。
难点:三角形内角和定理的证明。
复习引入
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,二哥突然不高兴,发起脾气来,它指着大哥说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”大哥说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?”
二哥很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
情景导入
锐角三角形
480
720
600
600+480+720=1800
(学生运用学科工具—量角器测量演示)
温故知新
A
B
C
2
1
小组合作,将三角形的三个内角剪下来拼合在一起,你有什么发现吗,你能证明你的发现吗?
探索新知
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证明猜想
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
2
1
证明猜想
证法2:延长BC到D,过点C作CE∥BA,
C
B
A
E
D
1
2
证明猜想
C
B
A
E
D
F
证法3:过D作DE∥AC,作DF∥AB.
想一想:同学们还有其他的方法吗?
证明猜想
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
归纳整理
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
B
G
C
2
4
A
3
E
D
F
H
1
试一试:同学们按照上图中的辅助线,给出证明步骤?
归纳整理
1.求出下列各图中的x值.
运用新知
如图,在△ABC中,
∠BAC=40
°,
∠B=75
°,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40
°,
AD是△ABC的角平分线,得
∠BAD=
∠BAC=20
°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°.
例题精讲
如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
跟踪训练
北
.
A
D
北
.
C
B
.
东
E
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80
°方向,C岛在B岛的北偏西40
°方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
例题精讲
如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
D
E
跟踪训练
1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一
样的玻璃,那么最省事的办法是
(
)
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
小试牛刀
2.如图,则∠1+∠2+∠3+∠4=___________
.
B
A
C
D
4
1
3
2
E
40°
(
小试牛刀
3.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
小试牛刀
小结回顾
1、运用平移角的原理证明三角形的内角和为180°。
2、证明命题的注意事项。
3、利用三角形的内角和解决方向角的有关问题。
2.在△ABC中,
∠A=
∠B+10°,
∠C=
∠A
+
10°,
则
∠A=
,
∠
B=
,∠
C=
.
(必做题)
1.课本第16页第4题(必做题)
作业布置
3.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.(选做题)
作业布置
