第四章 指数函数、对数函数与幂函数 能力提升单元测试-2021-2022学年高一上学期数学人教B版(2019)必修第二册(Word含答案)
文档属性
| 名称 | 第四章 指数函数、对数函数与幂函数 能力提升单元测试-2021-2022学年高一上学期数学人教B版(2019)必修第二册(Word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 462.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 19:40:18 | ||
图片预览


文档简介
第四章
指数函数、对数函数与幂函数
能力提升——2021-2022学年高一数学人教B版(2019)必修第二册单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设,则a,b,c的大小关系是(
)
A.
B.
C.
D.
2.已知,则(
)
A.
B.
C.
D.
3.下列函数:①②③④且其中,指数函数的个数是(???
)
A.1??????????B.2??????????C.3??????????D.4
4.若函数是指数函数,则实数m的值为(
)
A.2
B.1
C.3
D.2或-1
5.下列以为自变量的函数中,是指数函数的是(??
)
A.
B.
C.
D.
且
6.设都是正数,且,那么(
)
A.
B.
C.
D.
7.已知,则(
)
A.
B.
C.2
D.3
8.若函数的图像位于第一、二象限,则它的反函数的图像位于(
)
A.第一、二象限
B.第三、四象限
C.第二、三象限
D.第一、四象限
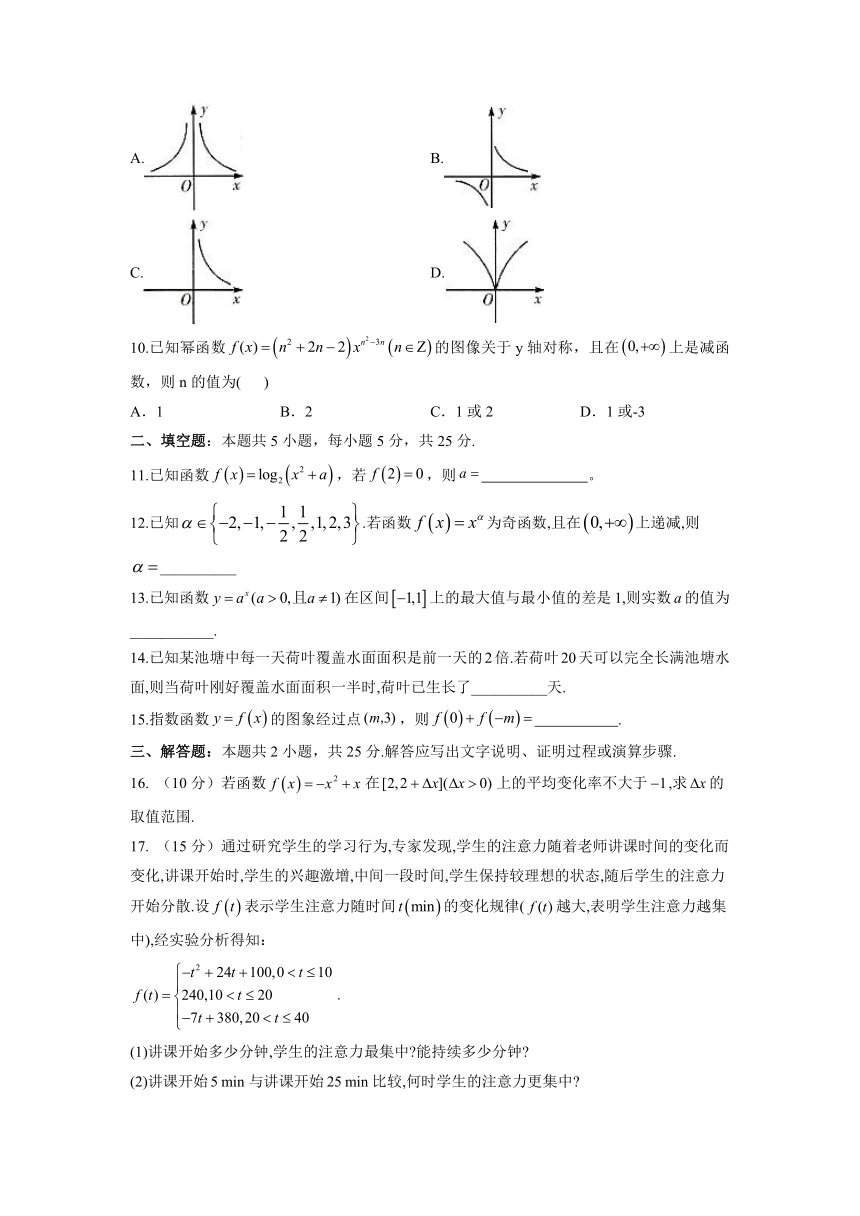
9.的图像是图中的(
)
A.
B.
C.
D.
10.已知幂函数的图像关于y轴对称,且在上是减函数,则n的值为(
)
A.1
B.2
C.1或2
D.1或-3
二、填空题:本题共5小题,每小题5分,共25分.
11.已知函数,若,则
。
12.已知.若函数为奇函数,且在上递减,则__________
13.已知函数在区间上的最大值与最小值的差是1,则实数a的值为___________.
14.已知某池塘中每一天荷叶覆盖水面面积是前一天的2倍.若荷叶20天可以完全长满池塘水面,则当荷叶刚好覆盖水面面积一半时,荷叶已生长了__________天.
15.指数函数的图象经过点,则
.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)若函数在上的平均变化率不大于,求的取值范围.
17.
(15分)通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间一段时间,学生保持较理想的状态,随后学生的注意力开始分散.设表示学生注意力随时间的变化规律(越大,表明学生注意力越集中),经实验分析得知:
.
(1)讲课开始多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始与讲课开始比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需要的状态下讲完这道题目?
答案以及解析
1.答案:A
解析:本题考查指数函数、对数函数的性质.因为,所以,即;因为,所以;因为,所以.综上,.故选A.
2.答案:B
解析:本题考查指数和对数的大小比较.因为所以故选B.
3.答案:A
解析:①是二次函数;②底数小于0,故不是指数函数;③指数为故不是指数函数;④是指数函数。
4.答案:D
解析:由题意可知,解得或.
5.答案:B
解析:指数函数的形式为且
6.答案:D
解析:本题考查指数与对数的互化、对数的定义及运算性质.若,则由a,b为正数可知,故A错误;由都是正数,故可设,则,即,去分母整理得,,故D正确,B,C错误.故选D.
7.答案:D
解析:本题考查指数式与对数式的互化、指数的运算.由题意,设,则,则,两边同时除以得,
即.解得或(舍去),得,因此,于是.故选D.
8.答案:D
解析:结合函数与反函数的图像关于直线对称,即可得出反函数位于第一、四象限.
9.答案:A
解析:因为,所以在上是减函数,而,所以定义域为.又,所以是偶函数,图像关于y轴对称,故选A.
10.答案:A
解析:函数为幂函数,
∴,解得或;
当时,,其图象关于y轴对称,且在上是减函数;
当时,,其图象关于y轴对称,但在上是增函数;
∴n的值应为1.
故答案为:A
11.答案:
解析:函数,,,解得.
12.答案:-1
解析:由为奇函数,故只能取,又在上递减,所以
13.答案:或
解析:当时,函数在区间上是增函数,则,
∵,∴;
当时,函数在区间上是减函数,则,
∵,∴.
综上,或.
14.答案:19
解析:假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y与生长时间x(天)的函数关系为,当时,荷叶长满水面,所以生长19天时,荷叶覆盖水面一半.
15.答案:
解析:设(且),
所以.且.
所以.
16.答案:函数在上的平均变化率为,由得.又因为,所以的取值范围是.
17.答案:(1)当时,单调递增,
当时,单调递减,且,
所以讲课开始,学生的注意力最集中,能持续.
(2)因为,
所以讲课开始比讲课开始学生的注意力更集中.
(3)当时,令,得,
当时,令,得,
又,
所以经过适当的安排,老师能在学生达到所需要的状态下讲完这道题目.
指数函数、对数函数与幂函数
能力提升——2021-2022学年高一数学人教B版(2019)必修第二册单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设,则a,b,c的大小关系是(
)
A.
B.
C.
D.
2.已知,则(
)
A.
B.
C.
D.
3.下列函数:①②③④且其中,指数函数的个数是(???
)
A.1??????????B.2??????????C.3??????????D.4
4.若函数是指数函数,则实数m的值为(
)
A.2
B.1
C.3
D.2或-1
5.下列以为自变量的函数中,是指数函数的是(??
)
A.
B.
C.
D.
且
6.设都是正数,且,那么(
)
A.
B.
C.
D.
7.已知,则(
)
A.
B.
C.2
D.3
8.若函数的图像位于第一、二象限,则它的反函数的图像位于(
)
A.第一、二象限
B.第三、四象限
C.第二、三象限
D.第一、四象限
9.的图像是图中的(
)
A.
B.
C.
D.
10.已知幂函数的图像关于y轴对称,且在上是减函数,则n的值为(
)
A.1
B.2
C.1或2
D.1或-3
二、填空题:本题共5小题,每小题5分,共25分.
11.已知函数,若,则
。
12.已知.若函数为奇函数,且在上递减,则__________
13.已知函数在区间上的最大值与最小值的差是1,则实数a的值为___________.
14.已知某池塘中每一天荷叶覆盖水面面积是前一天的2倍.若荷叶20天可以完全长满池塘水面,则当荷叶刚好覆盖水面面积一半时,荷叶已生长了__________天.
15.指数函数的图象经过点,则
.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)若函数在上的平均变化率不大于,求的取值范围.
17.
(15分)通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间一段时间,学生保持较理想的状态,随后学生的注意力开始分散.设表示学生注意力随时间的变化规律(越大,表明学生注意力越集中),经实验分析得知:
.
(1)讲课开始多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始与讲课开始比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需要的状态下讲完这道题目?
答案以及解析
1.答案:A
解析:本题考查指数函数、对数函数的性质.因为,所以,即;因为,所以;因为,所以.综上,.故选A.
2.答案:B
解析:本题考查指数和对数的大小比较.因为所以故选B.
3.答案:A
解析:①是二次函数;②底数小于0,故不是指数函数;③指数为故不是指数函数;④是指数函数。
4.答案:D
解析:由题意可知,解得或.
5.答案:B
解析:指数函数的形式为且
6.答案:D
解析:本题考查指数与对数的互化、对数的定义及运算性质.若,则由a,b为正数可知,故A错误;由都是正数,故可设,则,即,去分母整理得,,故D正确,B,C错误.故选D.
7.答案:D
解析:本题考查指数式与对数式的互化、指数的运算.由题意,设,则,则,两边同时除以得,
即.解得或(舍去),得,因此,于是.故选D.
8.答案:D
解析:结合函数与反函数的图像关于直线对称,即可得出反函数位于第一、四象限.
9.答案:A
解析:因为,所以在上是减函数,而,所以定义域为.又,所以是偶函数,图像关于y轴对称,故选A.
10.答案:A
解析:函数为幂函数,
∴,解得或;
当时,,其图象关于y轴对称,且在上是减函数;
当时,,其图象关于y轴对称,但在上是增函数;
∴n的值应为1.
故答案为:A
11.答案:
解析:函数,,,解得.
12.答案:-1
解析:由为奇函数,故只能取,又在上递减,所以
13.答案:或
解析:当时,函数在区间上是增函数,则,
∵,∴;
当时,函数在区间上是减函数,则,
∵,∴.
综上,或.
14.答案:19
解析:假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y与生长时间x(天)的函数关系为,当时,荷叶长满水面,所以生长19天时,荷叶覆盖水面一半.
15.答案:
解析:设(且),
所以.且.
所以.
16.答案:函数在上的平均变化率为,由得.又因为,所以的取值范围是.
17.答案:(1)当时,单调递增,
当时,单调递减,且,
所以讲课开始,学生的注意力最集中,能持续.
(2)因为,
所以讲课开始比讲课开始学生的注意力更集中.
(3)当时,令,得,
当时,令,得,
又,
所以经过适当的安排,老师能在学生达到所需要的状态下讲完这道题目.
