第五章 统计与概率基础夯实单元测试卷 -2021-2022学年高一上学期数学人教B版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 第五章 统计与概率基础夯实单元测试卷 -2021-2022学年高一上学期数学人教B版(2019)必修第二册(Word含答案解析) | 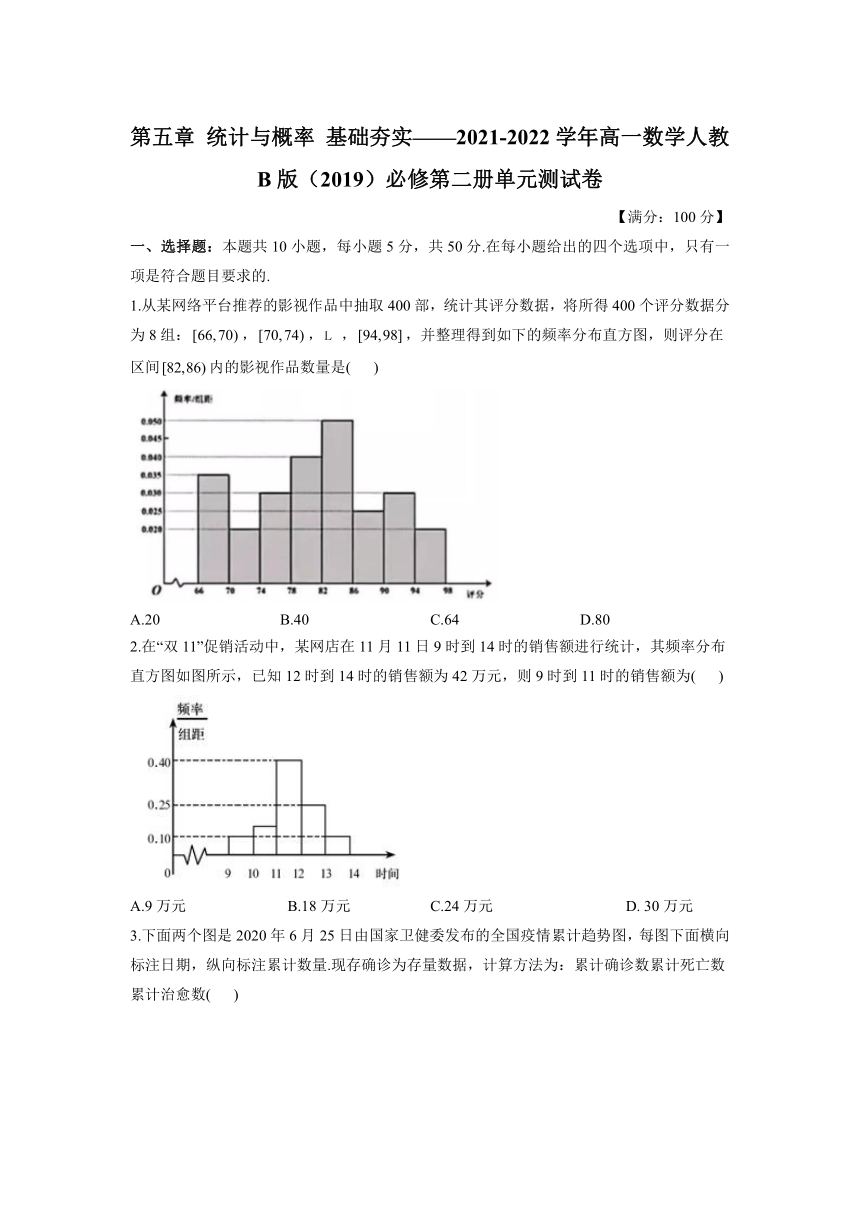 | |
| 格式 | doc | ||
| 文件大小 | 551.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 19:52:51 | ||
图片预览



文档简介
第五章
统计与概率
基础夯实——2021-2022学年高一数学人教B版(2019)必修第二册单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:,,,,并整理得到如下的频率分布直方图,则评分在区间内的影视作品数量是(
)
A.20
B.40
C.64
D.80
2.在“双11”促销活动中,某网店在11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为42万元,则9时到11时的销售额为(
)
A.9万元
B.18万元
C.24万元
D.
30万元
3.下面两个图是2020年6月25日由国家卫健委发布的全国疫情累计趋势图,每图下面横向标注日期,纵向标注累计数量.现存确诊为存量数据,计算方法为:累计确诊数累计死亡数累计治愈数(
)
则下列叙述错误的是(
)
A.自1月20日以来一个月内,全国累计确诊病例属于快速增长时期
B.自4月份以来,全国累计确诊病例增速缓慢,疫情扩散势头基本控制
C.自6月16日至24日以来,全国每日现存确诊病例平缓增加
D.自6月16日至24日以来,全国每日现存确诊病例逐步减少
4.为了解一片经济树林的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出样本的频率分布直方图如图所示.那么在这100株树木中,底部周长小于110cm的株数n是(
)
A.30
B.60
C.70
D.80
5.2021年将持续巩固脱贫攻坚成果,防止返贫,确保贫困人口稳步实现小康.某脱帽贫困县脱贫户相对集中,其中东南地区脱贫户占全县的28%,西北地区脱贫户占全县的52%,为精准了解本县脱贫户现状,“脱贫攻坚成果巩固”课题组拟深入到其中30户脱贫户家中调研,若按地区采用分层抽样的方法分配被调研的脱贫户,课题组应到其它地区(除本县东南和西北地区外)调研的脱贫户的户数是(
)
A.8人
B.7人
C.6人
D.5人
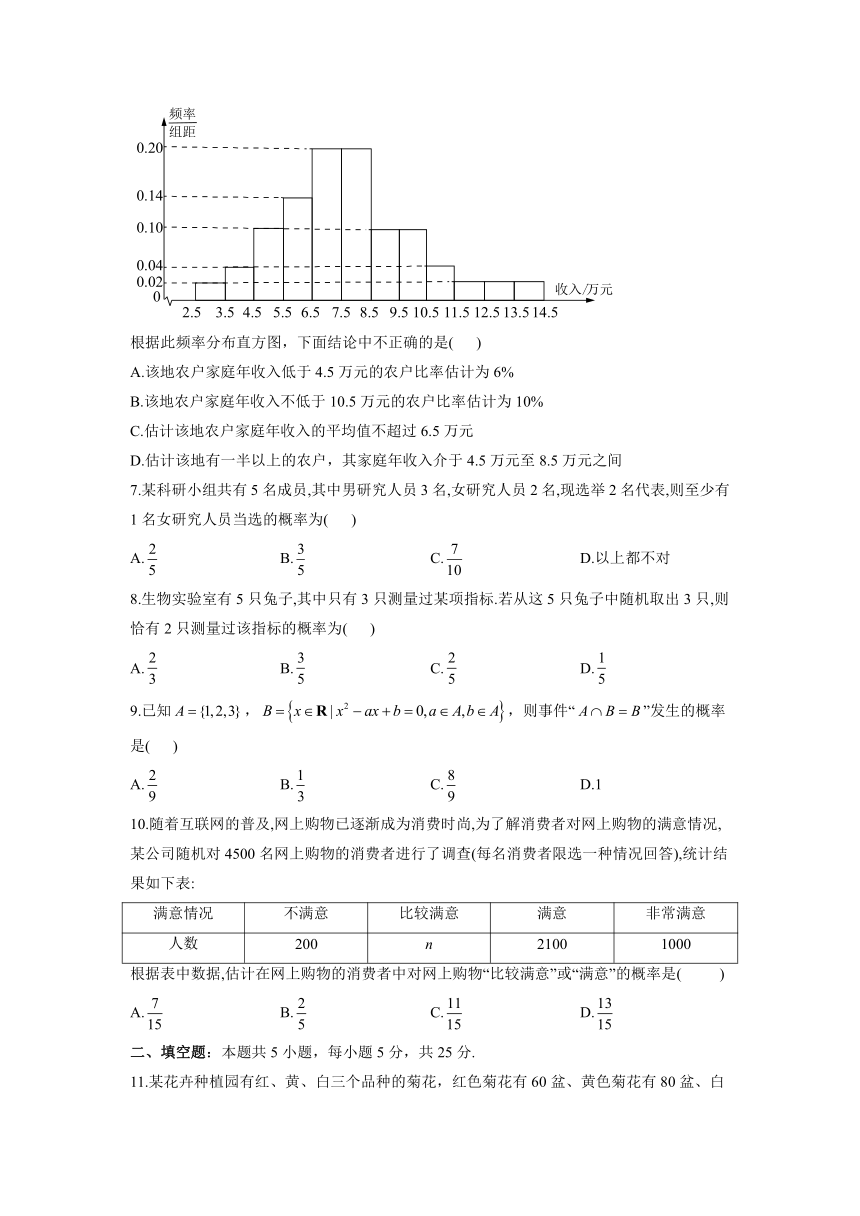
6.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调査,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是(
)
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
7.某科研小组共有5名成员,其中男研究人员3名,女研究人员2名,现选举2名代表,则至少有1名女研究人员当选的概率为(
)
A.
B.
C.
D.以上都不对
8.生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为(
)
A.
B.
C.
D.
9.已知,,则事件“”发生的概率是(
)
A.
B.
C.
D.1
10.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物的消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:
满意情况
不满意
比较满意
满意
非常满意
人数
200
n
2100
1000
根据表中数据,估计在网上购物的消费者中对网上购物“比较满意”或“满意”的概率是(
)
A.
B.
C.
D.
二、填空题:本题共5小题,每小题5分,共25分.
11.某花卉种植园有红、黄、白三个品种的菊花,红色菊花有60盆、黄色菊花有80盆、白色菊花有100盆,现要按照三种颜色菊花的数量比例用分层抽样的方法从中抽取48盆参加花展,则需要抽取______盆黄色菊花.
12.某公司有职800人,其中不到30岁的有120人,30岁到40岁的有400人,40岁以上的有280人.为了了解该公司职工与身体状况有关的某项指标,要从中抽取200名职工作为样本,职工年龄与这项指标有关,则应该选择的抽样方法是__________,40岁以上的职工应抽取________名.
13.甲、乙两人进行羽毛球比赛,采用三局两胜制(打满三局),已知甲每局比赛获胜的概率均为.现用计算机随机产生的之间的整数值来模拟甲和乙胜负的情况用0,1,2,3,4,5,6表示甲胜,用7,8,9表示乙胜由于是三局两胜制,所以以每3个随机数为一组,产生20组随机数:,,,,,,,,,,,,,,,,,,,.估计最终乙获胜的概率为____________.
14.从正六边形的6个顶点中随机选出4个,以它们作为顶点的四边形是矩形的概率为___________.
15.用数字1,2组成四位数,则数字1,2都出现的概率为_____________.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A,B,C,田忌的三匹马分别为a,b,c,三匹马各比赛一次,胜两场者获胜.若这六匹马的优劣程度可以用以下不等式表示:.
(1)正常情况下,求田忌获胜的概率;
(2)为了得到更大的获胜机会,田忌打探到齐王第一场必出上等马A,于是田忌采用了最恰当的应对策略,求这时田忌获胜的概率.
17.
(15分)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
男生
女生
支持
不支持
支持
不支持
方案一
200人
400人
300人
100人
方案二
350人
250人
150人
250人
假设所有学生对活动方案是否支持相互独立.
(1)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(2)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(3)将该校学生支持方案二的概率估计值记为,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为,试比较与的大小.(结论不要求证明)
答案以及解析
1.答案:D
解析:由图可知区间的频率为,数量即为部.
故选D.
2.答案:D
解析:时时对应的频率为:,总销售数为.
时时对应的频率为:,所以.
故选D.
3.答案:D
解析:由图一可知均正确.
由图二数据计算得6月16日的现存确诊病例数为,
同理可计算18、20、22、24日现存确诊病例数分别为346,383,441,473,故选D.
4.答案:C
解析:由题图可知周长小于110cm的频率为,因此在这100株树木中,底部周长小于110cm的株数.
5.答案:C
解析:课题组应到其他地区调研得脱贫户得户数为.故选C.
6.答案:C
解析:本题考查频率分布直方图、均值等统计图表及统计量的基础知识.
选项
正误
原因
A
√
由图可知,组距是1,前2个小矩形的面积和是0.06
B
√
最后4个小矩形的面积和是0.10
C
×
可以求得平均值是
D
√
4.5至8.5之间小矩形的面积和是0.64
7.答案:C
解析:设3名男研究人员为两名女研究人员为,则任选举2名代表有,共10种情况,其中至少有1名女研究人员当选的情况有7种,故所求概率.故选C.
8.答案:B
解析:设3只测量过某项指标的兔子为A,B,C,另外2只兔子为a,b,从这5只兔子中随机取出3只,则样本空间,共包含10个样本点,其中“恰有2只测量过该指标”包含的样本点共有6个,分别为,,,,,,因此所求的概率为,故选B.
9.答案:C
解析:,可能为,,,,,,.当时,,满足条件的a,b为,,2,3;,,3;,.当时,满足条件的a,b为,.当,时,没有满足条件的a,b.当时,满足条件的a,b为,.当,时,没有满足条件的a,b,∴事件“”发生的概率为.故选C.
10.答案:C
解析:由题意得,,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的总人数为,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的频率为.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为.故选C.
11.答案:16
解析:三个品种的菊花共有盆,需要抽取黄色菊花盆.
12.答案:分层抽样;70
解析:因为职工年龄与这项指标有关,所以应该选择分层抽样,且40岁以上的职工应抽取的人数为.
13.答案:
解析:20组随机数中含有7,8,9中的两个数字的有,,,,,,共6组,所以估计最终乙获胜的概率为.
14.答案:
解析:设正六边形为
ABCDEF,则从6个顶点中随机选出4个的样本空间,共15个样本点.其中能构成矩形的样本点有ABDE,ACDF,BCEF,共3个,所以所求概率为.
15.答案:
解析:用数字1,2组成四位数,共有16种不同的结果,数字1,2都出现的四位数有1112,1121,1211,2111,1122,1212,1221,2121,2112,2211,2221,2212,2122,1222,共14种.根据古典概型的概率计算公式,得数字1,2都出现的概率.
16.答案:(1)比赛配对的所有情况共有6种:,,,,,.
经分析:仅有配对为时,田忌获胜,则田忌获胜的概率为.
(2)田忌的策略是首场安排c出赛,此时比赛配对的所有情况有2种:,,配对为时,田忌获胜,则田忌获胜的概率为.
17.答案:(1)记“该校男生支持方案一”为事件,“该校女生支持方案一”为事件.
由于所有学生对活动方案是否支持相互独立,所以由表中数据可知抽取的男生总人数为,支持方案一的有200人,则估计该校男生支持方案一的概率.
抽取的女生总人数,支持方案一的有300人,则估计该校女生支持方案一的概率.
(2)记“从该校全体男生中随机抽取2人,全体女生中随机抽取1人,这3人中恰有2人支持方案一”为事件,则事件包含“一名男生支持,一名男生不支持,一名女生支持”、“两名男生支持,一名女生不支持”,由(1)可知
.
(3).
统计与概率
基础夯实——2021-2022学年高一数学人教B版(2019)必修第二册单元测试卷
【满分:100分】
一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:,,,,并整理得到如下的频率分布直方图,则评分在区间内的影视作品数量是(
)
A.20
B.40
C.64
D.80
2.在“双11”促销活动中,某网店在11月11日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知12时到14时的销售额为42万元,则9时到11时的销售额为(
)
A.9万元
B.18万元
C.24万元
D.
30万元
3.下面两个图是2020年6月25日由国家卫健委发布的全国疫情累计趋势图,每图下面横向标注日期,纵向标注累计数量.现存确诊为存量数据,计算方法为:累计确诊数累计死亡数累计治愈数(
)
则下列叙述错误的是(
)
A.自1月20日以来一个月内,全国累计确诊病例属于快速增长时期
B.自4月份以来,全国累计确诊病例增速缓慢,疫情扩散势头基本控制
C.自6月16日至24日以来,全国每日现存确诊病例平缓增加
D.自6月16日至24日以来,全国每日现存确诊病例逐步减少
4.为了解一片经济树林的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出样本的频率分布直方图如图所示.那么在这100株树木中,底部周长小于110cm的株数n是(
)
A.30
B.60
C.70
D.80
5.2021年将持续巩固脱贫攻坚成果,防止返贫,确保贫困人口稳步实现小康.某脱帽贫困县脱贫户相对集中,其中东南地区脱贫户占全县的28%,西北地区脱贫户占全县的52%,为精准了解本县脱贫户现状,“脱贫攻坚成果巩固”课题组拟深入到其中30户脱贫户家中调研,若按地区采用分层抽样的方法分配被调研的脱贫户,课题组应到其它地区(除本县东南和西北地区外)调研的脱贫户的户数是(
)
A.8人
B.7人
C.6人
D.5人
6.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调査,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是(
)
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
7.某科研小组共有5名成员,其中男研究人员3名,女研究人员2名,现选举2名代表,则至少有1名女研究人员当选的概率为(
)
A.
B.
C.
D.以上都不对
8.生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为(
)
A.
B.
C.
D.
9.已知,,则事件“”发生的概率是(
)
A.
B.
C.
D.1
10.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4500名网上购物的消费者进行了调查(每名消费者限选一种情况回答),统计结果如下表:
满意情况
不满意
比较满意
满意
非常满意
人数
200
n
2100
1000
根据表中数据,估计在网上购物的消费者中对网上购物“比较满意”或“满意”的概率是(
)
A.
B.
C.
D.
二、填空题:本题共5小题,每小题5分,共25分.
11.某花卉种植园有红、黄、白三个品种的菊花,红色菊花有60盆、黄色菊花有80盆、白色菊花有100盆,现要按照三种颜色菊花的数量比例用分层抽样的方法从中抽取48盆参加花展,则需要抽取______盆黄色菊花.
12.某公司有职800人,其中不到30岁的有120人,30岁到40岁的有400人,40岁以上的有280人.为了了解该公司职工与身体状况有关的某项指标,要从中抽取200名职工作为样本,职工年龄与这项指标有关,则应该选择的抽样方法是__________,40岁以上的职工应抽取________名.
13.甲、乙两人进行羽毛球比赛,采用三局两胜制(打满三局),已知甲每局比赛获胜的概率均为.现用计算机随机产生的之间的整数值来模拟甲和乙胜负的情况用0,1,2,3,4,5,6表示甲胜,用7,8,9表示乙胜由于是三局两胜制,所以以每3个随机数为一组,产生20组随机数:,,,,,,,,,,,,,,,,,,,.估计最终乙获胜的概率为____________.
14.从正六边形的6个顶点中随机选出4个,以它们作为顶点的四边形是矩形的概率为___________.
15.用数字1,2组成四位数,则数字1,2都出现的概率为_____________.
三、解答题:本题共2小题,共25分.解答应写出文字说明、证明过程或演算步骤.
16.
(10分)田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A,B,C,田忌的三匹马分别为a,b,c,三匹马各比赛一次,胜两场者获胜.若这六匹马的优劣程度可以用以下不等式表示:.
(1)正常情况下,求田忌获胜的概率;
(2)为了得到更大的获胜机会,田忌打探到齐王第一场必出上等马A,于是田忌采用了最恰当的应对策略,求这时田忌获胜的概率.
17.
(15分)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
男生
女生
支持
不支持
支持
不支持
方案一
200人
400人
300人
100人
方案二
350人
250人
150人
250人
假设所有学生对活动方案是否支持相互独立.
(1)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(2)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(3)将该校学生支持方案二的概率估计值记为,假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为,试比较与的大小.(结论不要求证明)
答案以及解析
1.答案:D
解析:由图可知区间的频率为,数量即为部.
故选D.
2.答案:D
解析:时时对应的频率为:,总销售数为.
时时对应的频率为:,所以.
故选D.
3.答案:D
解析:由图一可知均正确.
由图二数据计算得6月16日的现存确诊病例数为,
同理可计算18、20、22、24日现存确诊病例数分别为346,383,441,473,故选D.
4.答案:C
解析:由题图可知周长小于110cm的频率为,因此在这100株树木中,底部周长小于110cm的株数.
5.答案:C
解析:课题组应到其他地区调研得脱贫户得户数为.故选C.
6.答案:C
解析:本题考查频率分布直方图、均值等统计图表及统计量的基础知识.
选项
正误
原因
A
√
由图可知,组距是1,前2个小矩形的面积和是0.06
B
√
最后4个小矩形的面积和是0.10
C
×
可以求得平均值是
D
√
4.5至8.5之间小矩形的面积和是0.64
7.答案:C
解析:设3名男研究人员为两名女研究人员为,则任选举2名代表有,共10种情况,其中至少有1名女研究人员当选的情况有7种,故所求概率.故选C.
8.答案:B
解析:设3只测量过某项指标的兔子为A,B,C,另外2只兔子为a,b,从这5只兔子中随机取出3只,则样本空间,共包含10个样本点,其中“恰有2只测量过该指标”包含的样本点共有6个,分别为,,,,,,因此所求的概率为,故选B.
9.答案:C
解析:,可能为,,,,,,.当时,,满足条件的a,b为,,2,3;,,3;,.当时,满足条件的a,b为,.当,时,没有满足条件的a,b.当时,满足条件的a,b为,.当,时,没有满足条件的a,b,∴事件“”发生的概率为.故选C.
10.答案:C
解析:由题意得,,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的总人数为,所以随机调查的网上购物消费者中对网上购物“比较满意”或“满意”的频率为.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为.故选C.
11.答案:16
解析:三个品种的菊花共有盆,需要抽取黄色菊花盆.
12.答案:分层抽样;70
解析:因为职工年龄与这项指标有关,所以应该选择分层抽样,且40岁以上的职工应抽取的人数为.
13.答案:
解析:20组随机数中含有7,8,9中的两个数字的有,,,,,,共6组,所以估计最终乙获胜的概率为.
14.答案:
解析:设正六边形为
ABCDEF,则从6个顶点中随机选出4个的样本空间,共15个样本点.其中能构成矩形的样本点有ABDE,ACDF,BCEF,共3个,所以所求概率为.
15.答案:
解析:用数字1,2组成四位数,共有16种不同的结果,数字1,2都出现的四位数有1112,1121,1211,2111,1122,1212,1221,2121,2112,2211,2221,2212,2122,1222,共14种.根据古典概型的概率计算公式,得数字1,2都出现的概率.
16.答案:(1)比赛配对的所有情况共有6种:,,,,,.
经分析:仅有配对为时,田忌获胜,则田忌获胜的概率为.
(2)田忌的策略是首场安排c出赛,此时比赛配对的所有情况有2种:,,配对为时,田忌获胜,则田忌获胜的概率为.
17.答案:(1)记“该校男生支持方案一”为事件,“该校女生支持方案一”为事件.
由于所有学生对活动方案是否支持相互独立,所以由表中数据可知抽取的男生总人数为,支持方案一的有200人,则估计该校男生支持方案一的概率.
抽取的女生总人数,支持方案一的有300人,则估计该校女生支持方案一的概率.
(2)记“从该校全体男生中随机抽取2人,全体女生中随机抽取1人,这3人中恰有2人支持方案一”为事件,则事件包含“一名男生支持,一名男生不支持,一名女生支持”、“两名男生支持,一名女生不支持”,由(1)可知
.
(3).
