5.3 轴对称与坐标变化课件(共21张PPT)
文档属性
| 名称 | 5.3 轴对称与坐标变化课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第五章
位置与坐标
3
轴对称与坐标变化
知识点一
图形的坐标变化与轴对称
图形的坐标变化与轴对称的关系:
(1)横坐标保持不变,纵坐标分别乘-1,所得图形与原图形关于x轴成轴对称;
(2)纵坐标保持不变,横坐标分别乘-1,所得图形与原图形关于y轴成轴对称.
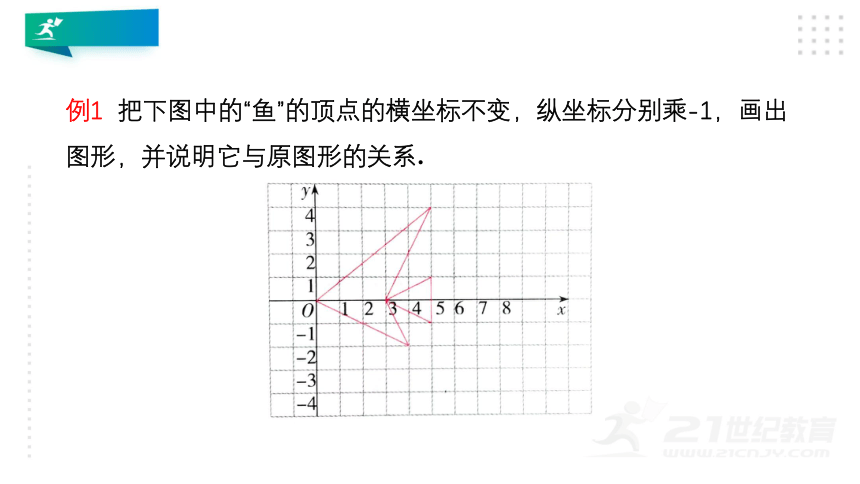
例1
把下图中的“鱼”的顶点的横坐标不变,纵坐标分别乘-1,画出图形,并说明它与原图形的关系.
解析
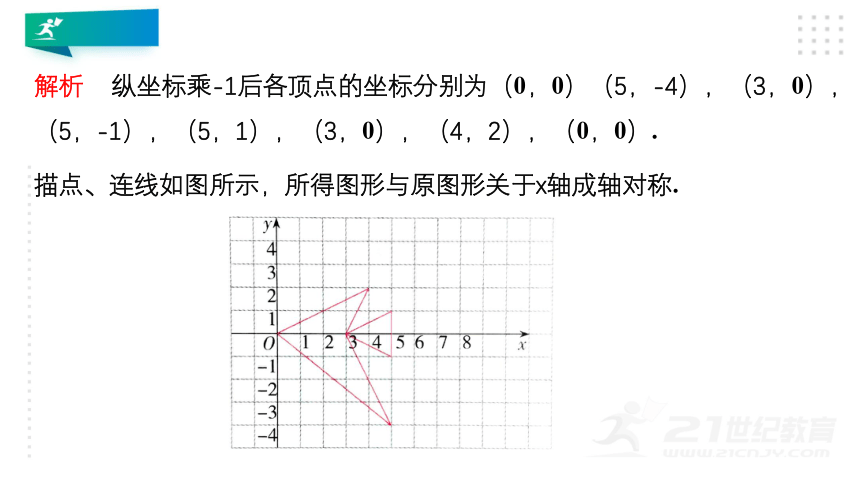
纵坐标乘-1后各顶点的坐标分别为(0,0)(5,-4),(3,0),(5,-1),(5,1),(3,0),(4,2),(0,0).
描点、连线如图所示,所得图形与原图形关于x轴成轴对称.
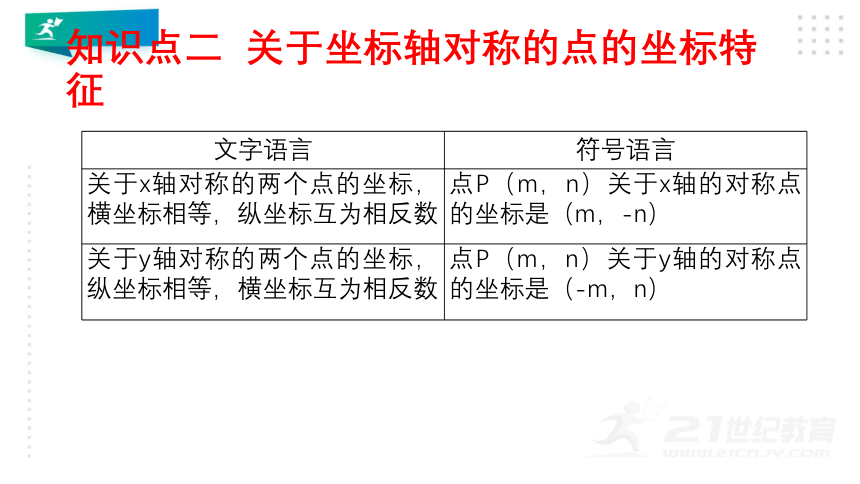
知识点二
关于坐标轴对称的点的坐标特征
文字语言
符号语言
关于x轴对称的两个点的坐标,横坐标相等,纵坐标互为相反数
点P(m,n)关于x轴的对称点的坐标是(m,-n)
关于y轴对称的两个点的坐标,纵坐标相等,横坐标互为相反数
点P(m,n)关于y轴的对称点的坐标是(-m,n)
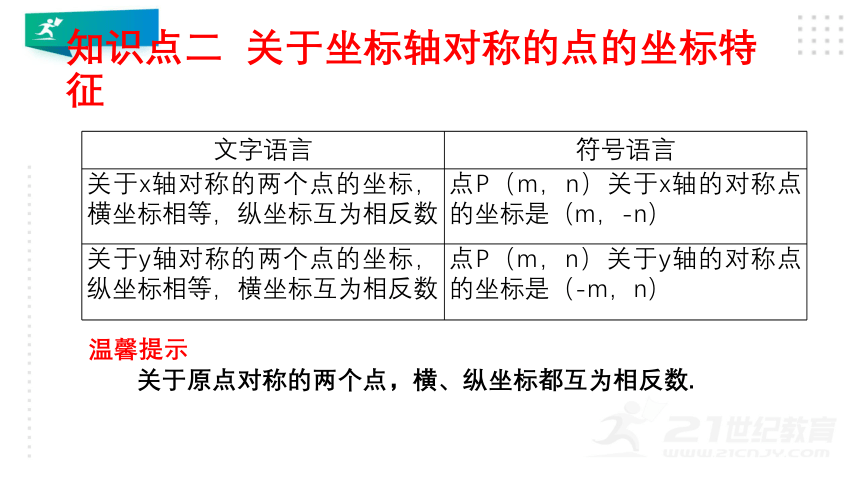
知识点二
关于坐标轴对称的点的坐标特征
文字语言
符号语言
关于x轴对称的两个点的坐标,横坐标相等,纵坐标互为相反数
点P(m,n)关于x轴的对称点的坐标是(m,-n)
关于y轴对称的两个点的坐标,纵坐标相等,横坐标互为相反数
点P(m,n)关于y轴的对称点的坐标是(-m,n)
温馨提示
关于原点对称的两个点,横、纵坐标都互为相反数.
例2
已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为__________.
例2
已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为__________.
解析
∵P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,解得a=3,b=-4,
则(a+b)2020=(3-4)2020=1.
例2
已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为____1_____.
解析
∵P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,解得a=3,b=-4,
则(a+b)2020=(3-4)2020=1.
经典例题
题型
坐标系中作已知图形关于坐标轴对称的图形
例题
如图所示,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(-3,0),B(-3,-3),C(-1,-3).在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F的坐标.
解析
D,E,F的坐标分别为D(-3,0),E(-3,3)F(-1,3).
所画图形如图所示,其中△DEF即为所求.
点拨
解决此类问题的关键是先确定各个顶点关于坐标轴对称的点的坐标,然后在平面直角坐标系中各对应点,顺次连接各点得到的图形就是所求作的图形.
易错易混
易错点
混淆图形的变化与坐标之间的关系
在平面直角坐标系中,图形关于x轴对称,点的横坐标相同,纵坐标互为相反数;图形关于y轴对称,点的纵坐标相同,横坐标互为相反数.
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
解析
因为平面直角坐标系中关于y轴对称的点的坐标特点:横坐标互为相反数,纵坐标不变,可得点A(-2,6)关于y轴对称的点B的坐标为(2,6).故选C.
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
C
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
解析
因为平面直角坐标系中关于y轴对称的点的坐标特点:横坐标互为相反数,纵坐标不变,可得点A(-2,6)关于y轴对称的点B的坐标为(2,6).故选C.
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
C
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
解析
因为平面直角坐标系中关于y轴对称的点的坐标特点:横坐标互为相反数,纵坐标不变,可得点A(-2,6)关于y轴对称的点B的坐标为(2,6).故选C.
易错分析
熟记图形的变化与点的坐标变化之间的关系,数形结合是解决此类问题的重要方法.
第五章
位置与坐标
3
轴对称与坐标变化
知识点一
图形的坐标变化与轴对称
图形的坐标变化与轴对称的关系:
(1)横坐标保持不变,纵坐标分别乘-1,所得图形与原图形关于x轴成轴对称;
(2)纵坐标保持不变,横坐标分别乘-1,所得图形与原图形关于y轴成轴对称.
例1
把下图中的“鱼”的顶点的横坐标不变,纵坐标分别乘-1,画出图形,并说明它与原图形的关系.
解析
纵坐标乘-1后各顶点的坐标分别为(0,0)(5,-4),(3,0),(5,-1),(5,1),(3,0),(4,2),(0,0).
描点、连线如图所示,所得图形与原图形关于x轴成轴对称.
知识点二
关于坐标轴对称的点的坐标特征
文字语言
符号语言
关于x轴对称的两个点的坐标,横坐标相等,纵坐标互为相反数
点P(m,n)关于x轴的对称点的坐标是(m,-n)
关于y轴对称的两个点的坐标,纵坐标相等,横坐标互为相反数
点P(m,n)关于y轴的对称点的坐标是(-m,n)
知识点二
关于坐标轴对称的点的坐标特征
文字语言
符号语言
关于x轴对称的两个点的坐标,横坐标相等,纵坐标互为相反数
点P(m,n)关于x轴的对称点的坐标是(m,-n)
关于y轴对称的两个点的坐标,纵坐标相等,横坐标互为相反数
点P(m,n)关于y轴的对称点的坐标是(-m,n)
温馨提示
关于原点对称的两个点,横、纵坐标都互为相反数.
例2
已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为__________.
例2
已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为__________.
解析
∵P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,解得a=3,b=-4,
则(a+b)2020=(3-4)2020=1.
例2
已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2020的值为____1_____.
解析
∵P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,解得a=3,b=-4,
则(a+b)2020=(3-4)2020=1.
经典例题
题型
坐标系中作已知图形关于坐标轴对称的图形
例题
如图所示,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(-3,0),B(-3,-3),C(-1,-3).在图中作出△ABC关于x轴对称的图形△DEF,并写出D,E,F的坐标.
解析
D,E,F的坐标分别为D(-3,0),E(-3,3)F(-1,3).
所画图形如图所示,其中△DEF即为所求.
点拨
解决此类问题的关键是先确定各个顶点关于坐标轴对称的点的坐标,然后在平面直角坐标系中各对应点,顺次连接各点得到的图形就是所求作的图形.
易错易混
易错点
混淆图形的变化与坐标之间的关系
在平面直角坐标系中,图形关于x轴对称,点的横坐标相同,纵坐标互为相反数;图形关于y轴对称,点的纵坐标相同,横坐标互为相反数.
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
解析
因为平面直角坐标系中关于y轴对称的点的坐标特点:横坐标互为相反数,纵坐标不变,可得点A(-2,6)关于y轴对称的点B的坐标为(2,6).故选C.
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
C
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
解析
因为平面直角坐标系中关于y轴对称的点的坐标特点:横坐标互为相反数,纵坐标不变,可得点A(-2,6)关于y轴对称的点B的坐标为(2,6).故选C.
例题
平面直角坐标系中,点A(-2,6)与点B关于y轴对称,则点B的坐标是(
C
)
A.(-2,6)
B.(-2,-6)
C.(2,6)
D.(2,-6)
解析
因为平面直角坐标系中关于y轴对称的点的坐标特点:横坐标互为相反数,纵坐标不变,可得点A(-2,6)关于y轴对称的点B的坐标为(2,6).故选C.
易错分析
熟记图形的变化与点的坐标变化之间的关系,数形结合是解决此类问题的重要方法.
