《第五章 位置与坐标》单元测试题(含答案)
文档属性
| 名称 | 《第五章 位置与坐标》单元测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 13:27:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《第五章
位置与坐标》单元测试题
(时间:60分钟
满分:100分)
一、选择题(每小题3分,共24分)
1下列说法中,能确定物体位置的是(
)
A.天空中的一只小鸟
B.电影院中18座
C.东经120°,北纬30°
D.北偏西35°方向
2.在平面直角坐标系中,点P(-2,-6)所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.点E(a,b)在第二象限,它到x轴的距离是4,到y轴的距离是3,则有(
)
A.a=3,b=4
B.a=-3,b=4
C.a=-4,b=3
D.a=4,b=-3
4.若=0,则点P(x,y)在(
)
A.横轴上
B去掉原点的横轴上
C.纵轴上
D.去掉原点的纵轴上
5.在平面直角坐标系xOy中,△ABC的顶点C的坐标为(3,-1),则点C关于x轴,y轴对称的点的坐标分别为(
)
A.(3,1),(-3,-1)
B.(-3,1),(-3,-1)
C.(3,1),(1,3)
D.(-3,-1),(3,1)
6.如图所示,若“马”所在位置的坐标为(-2,-1),“象”所在位置的坐标为(-1,1)则“兵”所在位置的坐标为(
)
A.(-2,1)
B.(-2,2)
C.(1,-2)
D.(2,-2)
7.如果长方形ABCD的中心与平面直角坐标系的原点重合,且点A和点B的坐标分别为(-2,3)和(2,3),则长方形ABCD的面积为(
)
A.32
B.24
C.16
D.8
8.如图所示,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于,MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为(
)
A.a=b
B.2a+b=-1
C.2a-b=1
D.2a+b=1
二、填空题(每小题4分,共24分
9.某小区用有序数对(5,2)表示5号楼2单元的住户,那么(9,3)表示的是_____号楼_______单元的住户.
10.若点P(x,y)在第四象限,且x2=4,|y|=3,则P点的坐标为_________________.
11.点A、B是平面直角坐标系中x轴上的两点,且AB=2,有一点P与AB构成三角形,若△PAB的面积为3,则点P的纵坐标为__________.
12.已知点A(m-1,-5)和点B(2,m+1),若直线AB∥x轴,则线段AB的长为________.
13.在平面直角坐标系中放置了一个边长为的正方形,如图所示,点B在y轴上,且坐标是(0,2),点C在x轴上,则点D的坐标为__________.
14.如图所示,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是_________.(点D不与点C重合)
三、解答题(共52分)
15.(8分)已知点O(0,0),B(1,2),点A在坐标轴上,且S△OAB=2,试求出所有满足条件的点A的坐标.
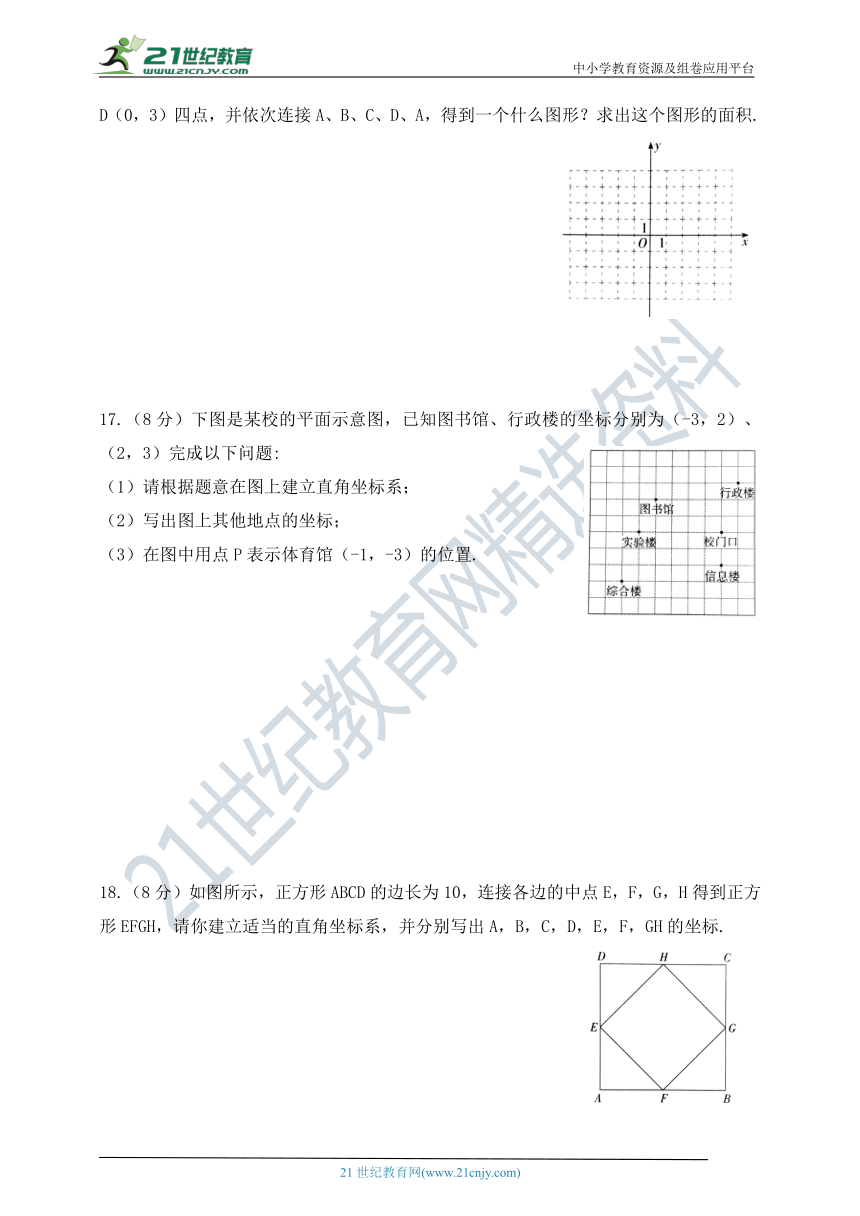
16.(8分)在如图所示的平面直角坐标系中描出A(-1,0),B(5,0),C(2,3),D(0,3)四点,并依次连接A、B、C、D、A,得到一个什么图形?求出这个图形的面积.
17.(8分)下图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2)、(2,3)完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标;
(3)在图中用点P表示体育馆(-1,-3)的位置.
18.(8分)如图所示,正方形ABCD的边长为10,连接各边的中点E,F,G,H得到正方形EFGH,请你建立适当的直角坐标系,并分别写出A,B,C,D,E,F,GH的坐标.
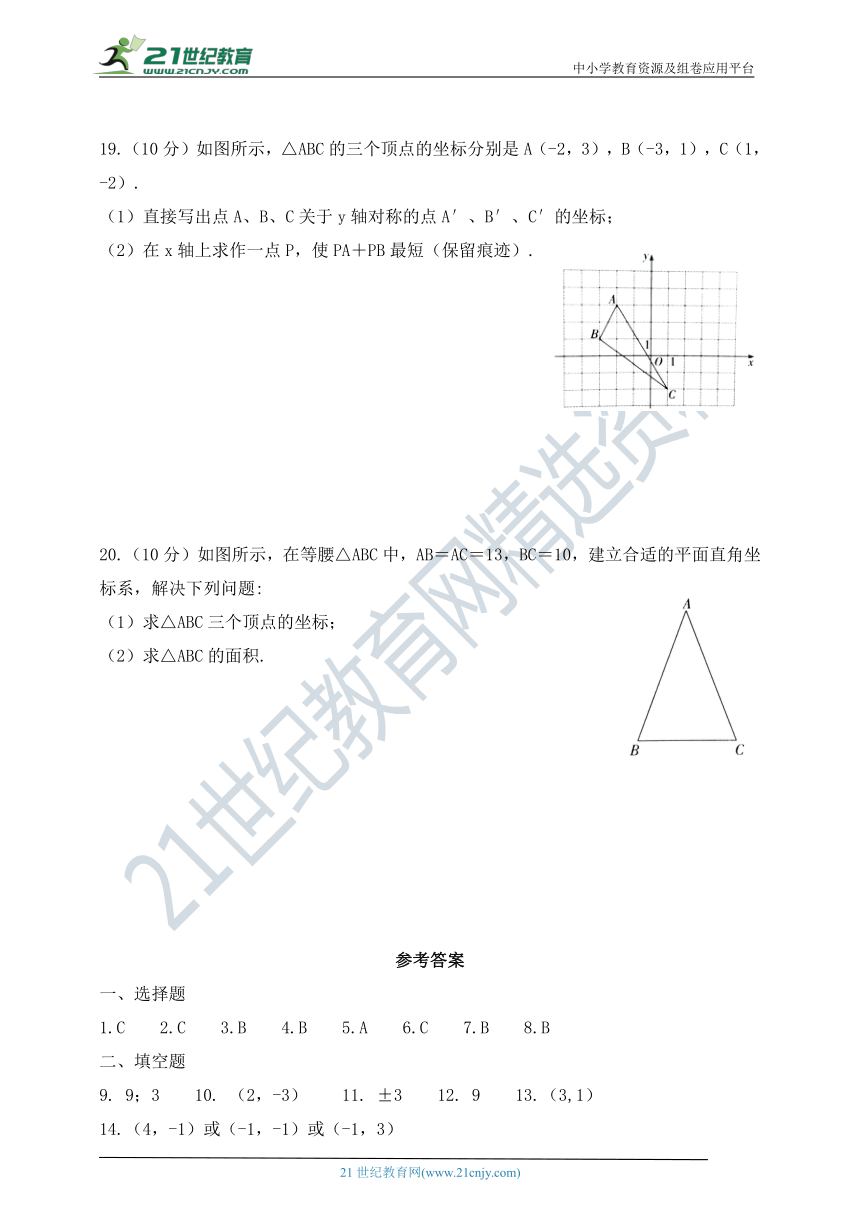
19.(10分)如图所示,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
(1)直接写出点A、B、C关于y轴对称的点A′、B′、C′的坐标;
(2)在x轴上求作一点P,使PA+PB最短(保留痕迹).
20.(10分)如图所示,在等腰△ABC中,AB=AC=13,BC=10,建立合适的平面直角坐标系,解决下列问题:
(1)求△ABC三个顶点的坐标;
(2)求△ABC的面积.
参考答案
一、选择题
1.C
2.C
3.B
4.B
5.A
6.C
7.B
8.B
二、填空题
9.
9;3
10.
(2,-3)
11.
±3
12.
9
13.(3,1)
14.(4,-1)或(-1,-1)或(-1,3)
三、解答题
15.解析
若点A在x轴上,则S△OAB=OA×2=2,解得OA=2,
所以点A的坐标为(2,0)或(-2,0).
若点A在y轴上,则S△OAB=OA×1=2,解得OA=4,
所以点A的坐标为(0,4)或(0,-4).
综上所述,点A的坐标为(2,0)或(-2,0)或(0,4)或(0,-4).
16.解析
如图,∵A(-1,0),B(5,0),C(2,3),D(0,3),
∴CD//AB,
CD=2,
AB=6,
DO=3,
易知四边形ABCD是一个梯形,
∴S梯形ABCD=×(CD+AB)×3=×8×3=12.
17.解析
(1)建立直角坐标系如图所示.
(2)根据坐标系得,校门口(1,0),实验楼(-4,0),综合楼(-5,-3),信息楼(1,-2).
(3)如图所示,P点即为所求.
18.解析
答案不唯一,如:以EG所在直线为x轴,以FH所在直线为y轴,建立如图所示的直角坐标系,则A,B,C,D,E,F,G,H的坐标分别为A(-5,-5),B(5,-5),C(5,5),D(-5,5),E(-5,0),F(0,-5),G(5,0),H(0,5).
19.解析
(1)A′(2,3),B′(3,1),C′(-1,-2).
(2)如图,作点B关于x轴的对称点B1.
连接AB1,交x轴于点P,连接BP,此时PA+PB最短,则点P即为所求.
20.解析
(1)建立坐标系不唯一,以点B为原点,BC所在的直线为x轴建立平面直角坐标系,如图,过点A作AD⊥BC于D,
∵AB=AC=13,BC=10,∴BD=CD=BC=×10=5,
由勾股定理得AD2=AB2-BD2=132-52=144,∴AD=12,
∴A(5,12),B(0,0),C(10,0)
(2)易知AD=12,则S△ABC=BC·AD=×10×12=60.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
《第五章
位置与坐标》单元测试题
(时间:60分钟
满分:100分)
一、选择题(每小题3分,共24分)
1下列说法中,能确定物体位置的是(
)
A.天空中的一只小鸟
B.电影院中18座
C.东经120°,北纬30°
D.北偏西35°方向
2.在平面直角坐标系中,点P(-2,-6)所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.点E(a,b)在第二象限,它到x轴的距离是4,到y轴的距离是3,则有(
)
A.a=3,b=4
B.a=-3,b=4
C.a=-4,b=3
D.a=4,b=-3
4.若=0,则点P(x,y)在(
)
A.横轴上
B去掉原点的横轴上
C.纵轴上
D.去掉原点的纵轴上
5.在平面直角坐标系xOy中,△ABC的顶点C的坐标为(3,-1),则点C关于x轴,y轴对称的点的坐标分别为(
)
A.(3,1),(-3,-1)
B.(-3,1),(-3,-1)
C.(3,1),(1,3)
D.(-3,-1),(3,1)
6.如图所示,若“马”所在位置的坐标为(-2,-1),“象”所在位置的坐标为(-1,1)则“兵”所在位置的坐标为(
)
A.(-2,1)
B.(-2,2)
C.(1,-2)
D.(2,-2)
7.如果长方形ABCD的中心与平面直角坐标系的原点重合,且点A和点B的坐标分别为(-2,3)和(2,3),则长方形ABCD的面积为(
)
A.32
B.24
C.16
D.8
8.如图所示,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于,MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为(
)
A.a=b
B.2a+b=-1
C.2a-b=1
D.2a+b=1
二、填空题(每小题4分,共24分
9.某小区用有序数对(5,2)表示5号楼2单元的住户,那么(9,3)表示的是_____号楼_______单元的住户.
10.若点P(x,y)在第四象限,且x2=4,|y|=3,则P点的坐标为_________________.
11.点A、B是平面直角坐标系中x轴上的两点,且AB=2,有一点P与AB构成三角形,若△PAB的面积为3,则点P的纵坐标为__________.
12.已知点A(m-1,-5)和点B(2,m+1),若直线AB∥x轴,则线段AB的长为________.
13.在平面直角坐标系中放置了一个边长为的正方形,如图所示,点B在y轴上,且坐标是(0,2),点C在x轴上,则点D的坐标为__________.
14.如图所示,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是_________.(点D不与点C重合)
三、解答题(共52分)
15.(8分)已知点O(0,0),B(1,2),点A在坐标轴上,且S△OAB=2,试求出所有满足条件的点A的坐标.
16.(8分)在如图所示的平面直角坐标系中描出A(-1,0),B(5,0),C(2,3),D(0,3)四点,并依次连接A、B、C、D、A,得到一个什么图形?求出这个图形的面积.
17.(8分)下图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2)、(2,3)完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标;
(3)在图中用点P表示体育馆(-1,-3)的位置.
18.(8分)如图所示,正方形ABCD的边长为10,连接各边的中点E,F,G,H得到正方形EFGH,请你建立适当的直角坐标系,并分别写出A,B,C,D,E,F,GH的坐标.
19.(10分)如图所示,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
(1)直接写出点A、B、C关于y轴对称的点A′、B′、C′的坐标;
(2)在x轴上求作一点P,使PA+PB最短(保留痕迹).
20.(10分)如图所示,在等腰△ABC中,AB=AC=13,BC=10,建立合适的平面直角坐标系,解决下列问题:
(1)求△ABC三个顶点的坐标;
(2)求△ABC的面积.
参考答案
一、选择题
1.C
2.C
3.B
4.B
5.A
6.C
7.B
8.B
二、填空题
9.
9;3
10.
(2,-3)
11.
±3
12.
9
13.(3,1)
14.(4,-1)或(-1,-1)或(-1,3)
三、解答题
15.解析
若点A在x轴上,则S△OAB=OA×2=2,解得OA=2,
所以点A的坐标为(2,0)或(-2,0).
若点A在y轴上,则S△OAB=OA×1=2,解得OA=4,
所以点A的坐标为(0,4)或(0,-4).
综上所述,点A的坐标为(2,0)或(-2,0)或(0,4)或(0,-4).
16.解析
如图,∵A(-1,0),B(5,0),C(2,3),D(0,3),
∴CD//AB,
CD=2,
AB=6,
DO=3,
易知四边形ABCD是一个梯形,
∴S梯形ABCD=×(CD+AB)×3=×8×3=12.
17.解析
(1)建立直角坐标系如图所示.
(2)根据坐标系得,校门口(1,0),实验楼(-4,0),综合楼(-5,-3),信息楼(1,-2).
(3)如图所示,P点即为所求.
18.解析
答案不唯一,如:以EG所在直线为x轴,以FH所在直线为y轴,建立如图所示的直角坐标系,则A,B,C,D,E,F,G,H的坐标分别为A(-5,-5),B(5,-5),C(5,5),D(-5,5),E(-5,0),F(0,-5),G(5,0),H(0,5).
19.解析
(1)A′(2,3),B′(3,1),C′(-1,-2).
(2)如图,作点B关于x轴的对称点B1.
连接AB1,交x轴于点P,连接BP,此时PA+PB最短,则点P即为所求.
20.解析
(1)建立坐标系不唯一,以点B为原点,BC所在的直线为x轴建立平面直角坐标系,如图,过点A作AD⊥BC于D,
∵AB=AC=13,BC=10,∴BD=CD=BC=×10=5,
由勾股定理得AD2=AB2-BD2=132-52=144,∴AD=12,
∴A(5,12),B(0,0),C(10,0)
(2)易知AD=12,则S△ABC=BC·AD=×10×12=60.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
