5.2.1《方程的意义》教案(含反思)
文档属性
| 名称 | 5.2.1《方程的意义》教案(含反思) |

|
|
| 格式 | docx | ||
| 文件大小 | 412.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览

文档简介
5.2.1《方程的意义》
教学目标
知识与技能
1.初步理解方程的意义,明确方程与等式的关系。
2.会判断一个式子是不是方程。
过程与方法
1.经历由天平称物体抽象出方程的过程,体会观察、比较、分析的学习方法。
2.在自主探究的学习过程中,让学生体会分类思想。
情感、态度与价值观
1.培养学生认真观察、积极思考的学习态度,增强学生的合作意识。
2.让学生感受方程与生活的密切联系,发展其抽象思维能力和符号感。
重点难点
重点:理解方程的意义。
难点:掌握判断一个式子是不是方程的方法。
课前准备
教师准备 天平 PPT课件
学生准备 小黑板
教学过程
板块一 创设情境,引入新知
师:同学们,日常生活中,你们见过哪些两侧平衡的现象?(天平、跷跷板)
师:老师这里有一架天平,在什么情况下,天平才能平衡呢?(两边一样重时,天平才能平衡。)
师:天平平衡时,如何用数学等式来表示呢?今天,我们就来学习新知识。(板书课题:方程的意义)
操作指导
通过学生熟知的天平,初步感知两边平衡、两边相等的概念。为学习方程的意义做了铺垫。
板块二 合作交流,抽象模型
活动1 观察思考,体会等式与不等式
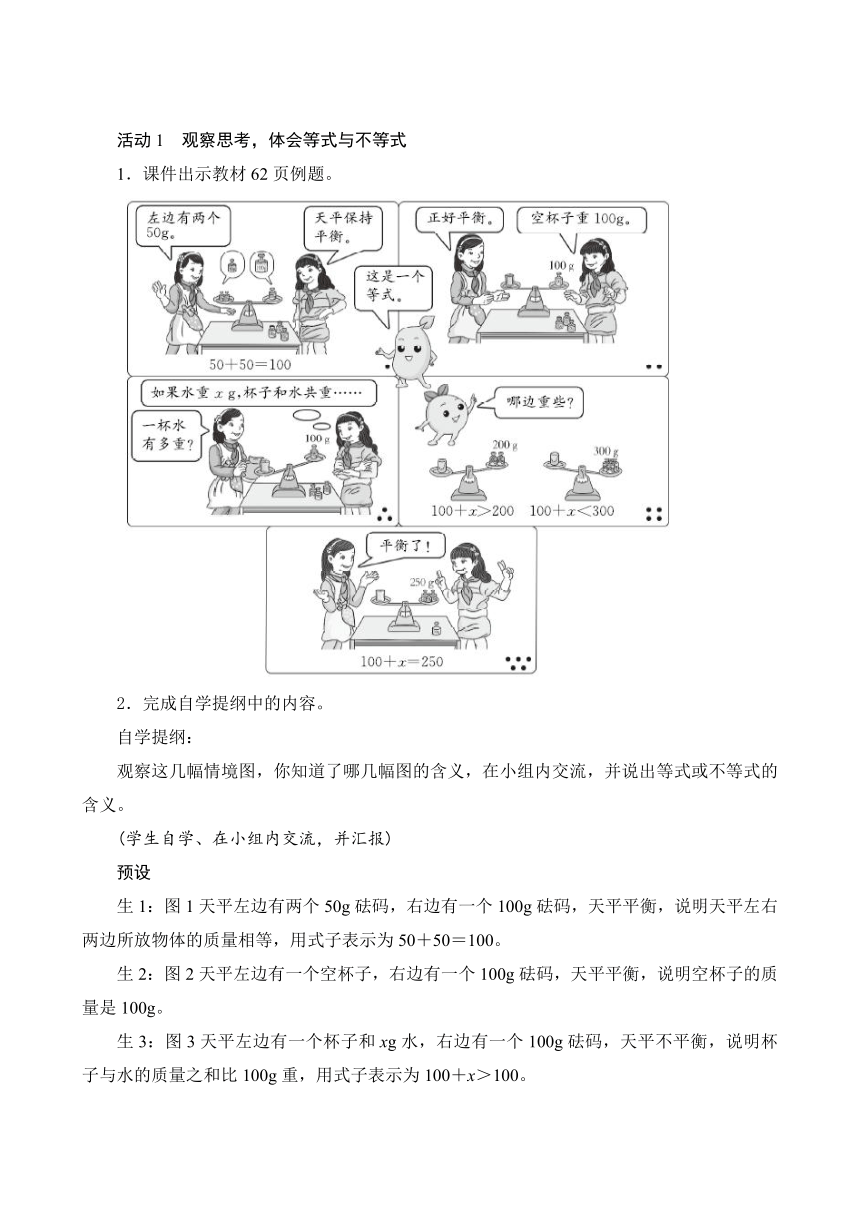
1.课件出示教材62页例题。
2.完成自学提纲中的内容。
自学提纲:
观察这几幅情境图,你知道了哪几幅图的含义,在小组内交流,并说出等式或不等式的含义。
(学生自学、在小组内交流,并汇报)
预设
生1:图1天平左边有两个50g砝码,右边有一个100g砝码,天平平衡,说明天平左右两边所放物体的质量相等,用式子表示为50+50=100。
生2:图2天平左边有一个空杯子,右边有一个100g砝码,天平平衡,说明空杯子的质量是100g。
生3:图3天平左边有一个杯子和xg水,右边有一个100g砝码,天平不平衡,说明杯子与水的质量之和比100g重,用式子表示为100+x>100。
生4:图4两架天平都不平衡,第一架天平用式子表示为100+x>200;第二架天平用式子表示为100+x<300。
生5:图5天平平衡,用式子表示为100+x=250。
师:根据情境图列出的式子中哪些是等式?哪个是含有未知数的等式?
预设
生1:50+50=100,100+x=250是等式。
生2:100+x=250是含有未知数的等式。
活动2 理解方程的意义
师:利用天平我们列出了等式,还列出了含有未知数的等式,那么,离开天平是否还可以列出含有未知数的等式呢?请同学们第二次自学,并完成自学提纲中的内容。
1.课件出示教材63页例题。
像100+x=250,3x=2.4……这样,含有未知数的等式就是方程。
2.完成自学提纲中的内容。
自学提纲:
(1)根据练习本图列出等式。
(2)什么是方程?方程应具备哪几个基本条件?
(3)完成教材63页“做一做”1题。
(4)自己尝试写出几个方程。
(学生自学、交流、汇报)
预设
生1:每本练习本x元,有3本练习本,就是x×3,写成3x,一共是2.4元,所以列出等式为3x=2.4。
生2:像100+x=250,3x=2.4……这样,含有未知数的等式就是方程。方程应具备的基本条件是含有未知数,还要是等式。
生3:5x+32=47,6(y+2)=42是方程。
3.整理分类,加深理解。
(1)组织学生分组活动,根据黑板上的算式特点进行分类。
(2)交流汇报,说出分类依据。
4.独立思考,汇报订正。
(1)独立完成教材63页“做一做”2题,并汇报,集体订正。
(2)判断0=5z-15是不是方程。
5.引导发现,概括总结。
(1)任何字母都可以作为未知数,而且在一个方程中可以出现2个或2个以上的未知数。
(2)未知数可以出现在等号的左右两边。
操作指导
教师先让学生观察教材插图中的小朋友们都写了哪些方程,通过交流,使学生明确判断一个式子是不是方程的两个要素:一看是不是等式,二看有没有未知数。在练习中,教师要随机应变,注意提问学生“方程应该具备哪几个基本条件”。如果一部分同学答对,一部分同学答错。这时教师可以先找答错的一名同学汇报讲解。讲解时随时和其他的同学互动交流,在同学们的讨论过程中,教师应适时引导、提问,指导学生判断正误的方法。
板块三 巩固练习,拓展延伸
1.完成教材66页1题。(引导学生明确方程必须具备的两个基本条件,缺一不可)
2.你会根据下面的图列出方程吗?
板块四 课堂总结,布置作业
1.课堂总结。
同学们这节课表现得都很不错。利用方程还可以解决我们生活中许多较为复杂的问题,希望同学们在今后的学习中继续发扬自主探究的学习精神。
2.布置作业。
教材66页3题。
板书设计
方程的意义
不是等式 是等式
100+x>200
100+x=250
100+x<300
像100+x=250,3x=2.4……这样,含有未知数的等式就是方程。
教学反思
本节课教师没有将等式、方程的概念强加给学生,而是充分尊重学生的原有知识水平,结合具体情境,运用天平平衡的原理来解释各数量之间的相等关系,按照教材上的连环画,学生一步一步观察,思考每个步骤的数学含义,逐步理解式子中的“=”表示天平平衡,从而初步体会方程的意义。在学生明确方程的意义后,教师引导学生自己写方程,识别方程并说出理由,进一步理解方程的意义,明确判断一个式子是不是方程的两个要素:一看是不是等式,二看有没有未知数。教师要注意的是,如果学生写出了含有两个未知数的方程,那么教师要及时说明是二元一次方程,也是方程。
教学目标
知识与技能
1.初步理解方程的意义,明确方程与等式的关系。
2.会判断一个式子是不是方程。
过程与方法
1.经历由天平称物体抽象出方程的过程,体会观察、比较、分析的学习方法。
2.在自主探究的学习过程中,让学生体会分类思想。
情感、态度与价值观
1.培养学生认真观察、积极思考的学习态度,增强学生的合作意识。
2.让学生感受方程与生活的密切联系,发展其抽象思维能力和符号感。
重点难点
重点:理解方程的意义。
难点:掌握判断一个式子是不是方程的方法。
课前准备
教师准备 天平 PPT课件
学生准备 小黑板
教学过程
板块一 创设情境,引入新知
师:同学们,日常生活中,你们见过哪些两侧平衡的现象?(天平、跷跷板)
师:老师这里有一架天平,在什么情况下,天平才能平衡呢?(两边一样重时,天平才能平衡。)
师:天平平衡时,如何用数学等式来表示呢?今天,我们就来学习新知识。(板书课题:方程的意义)
操作指导
通过学生熟知的天平,初步感知两边平衡、两边相等的概念。为学习方程的意义做了铺垫。
板块二 合作交流,抽象模型
活动1 观察思考,体会等式与不等式
1.课件出示教材62页例题。
2.完成自学提纲中的内容。
自学提纲:
观察这几幅情境图,你知道了哪几幅图的含义,在小组内交流,并说出等式或不等式的含义。
(学生自学、在小组内交流,并汇报)
预设
生1:图1天平左边有两个50g砝码,右边有一个100g砝码,天平平衡,说明天平左右两边所放物体的质量相等,用式子表示为50+50=100。
生2:图2天平左边有一个空杯子,右边有一个100g砝码,天平平衡,说明空杯子的质量是100g。
生3:图3天平左边有一个杯子和xg水,右边有一个100g砝码,天平不平衡,说明杯子与水的质量之和比100g重,用式子表示为100+x>100。
生4:图4两架天平都不平衡,第一架天平用式子表示为100+x>200;第二架天平用式子表示为100+x<300。
生5:图5天平平衡,用式子表示为100+x=250。
师:根据情境图列出的式子中哪些是等式?哪个是含有未知数的等式?
预设
生1:50+50=100,100+x=250是等式。
生2:100+x=250是含有未知数的等式。
活动2 理解方程的意义
师:利用天平我们列出了等式,还列出了含有未知数的等式,那么,离开天平是否还可以列出含有未知数的等式呢?请同学们第二次自学,并完成自学提纲中的内容。
1.课件出示教材63页例题。
像100+x=250,3x=2.4……这样,含有未知数的等式就是方程。
2.完成自学提纲中的内容。
自学提纲:
(1)根据练习本图列出等式。
(2)什么是方程?方程应具备哪几个基本条件?
(3)完成教材63页“做一做”1题。
(4)自己尝试写出几个方程。
(学生自学、交流、汇报)
预设
生1:每本练习本x元,有3本练习本,就是x×3,写成3x,一共是2.4元,所以列出等式为3x=2.4。
生2:像100+x=250,3x=2.4……这样,含有未知数的等式就是方程。方程应具备的基本条件是含有未知数,还要是等式。
生3:5x+32=47,6(y+2)=42是方程。
3.整理分类,加深理解。
(1)组织学生分组活动,根据黑板上的算式特点进行分类。
(2)交流汇报,说出分类依据。
4.独立思考,汇报订正。
(1)独立完成教材63页“做一做”2题,并汇报,集体订正。
(2)判断0=5z-15是不是方程。
5.引导发现,概括总结。
(1)任何字母都可以作为未知数,而且在一个方程中可以出现2个或2个以上的未知数。
(2)未知数可以出现在等号的左右两边。
操作指导
教师先让学生观察教材插图中的小朋友们都写了哪些方程,通过交流,使学生明确判断一个式子是不是方程的两个要素:一看是不是等式,二看有没有未知数。在练习中,教师要随机应变,注意提问学生“方程应该具备哪几个基本条件”。如果一部分同学答对,一部分同学答错。这时教师可以先找答错的一名同学汇报讲解。讲解时随时和其他的同学互动交流,在同学们的讨论过程中,教师应适时引导、提问,指导学生判断正误的方法。
板块三 巩固练习,拓展延伸
1.完成教材66页1题。(引导学生明确方程必须具备的两个基本条件,缺一不可)
2.你会根据下面的图列出方程吗?
板块四 课堂总结,布置作业
1.课堂总结。
同学们这节课表现得都很不错。利用方程还可以解决我们生活中许多较为复杂的问题,希望同学们在今后的学习中继续发扬自主探究的学习精神。
2.布置作业。
教材66页3题。
板书设计
方程的意义
不是等式 是等式
100+x>200
100+x=250
100+x<300
像100+x=250,3x=2.4……这样,含有未知数的等式就是方程。
教学反思
本节课教师没有将等式、方程的概念强加给学生,而是充分尊重学生的原有知识水平,结合具体情境,运用天平平衡的原理来解释各数量之间的相等关系,按照教材上的连环画,学生一步一步观察,思考每个步骤的数学含义,逐步理解式子中的“=”表示天平平衡,从而初步体会方程的意义。在学生明确方程的意义后,教师引导学生自己写方程,识别方程并说出理由,进一步理解方程的意义,明确判断一个式子是不是方程的两个要素:一看是不是等式,二看有没有未知数。教师要注意的是,如果学生写出了含有两个未知数的方程,那么教师要及时说明是二元一次方程,也是方程。
