数学人教A版(2019)必修第一册教案 4.4.2 对数函数的图像和性质( 表格式)
文档属性
| 名称 | 数学人教A版(2019)必修第一册教案 4.4.2 对数函数的图像和性质( 表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 261.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 20:54:47 | ||
图片预览


文档简介
第四章
指数函数与对数函数
4.4.2
对数函数的图像和性质
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.4.2节《对数函数的图像和性质》
是高中数学在指数函数之后的重要初等函数之一。对数函数与指数函数联系密切,无论是研究的思想方法方法还是图像及性质,都有其共通之处。相较于指数函数,对数函数的图象亦有其独特的美感。在类比推理的过程中,感受图像的变化,认识变化的规律,这是提高学生直观想象能力的一个重要的过程。为之后学习数学提供了更多角度的分析方法。培养和发展学生逻辑推理、数学直观、数学抽象、和数学建模的核心素养。
课程目标
学科素养
1、掌握对数函数的图像和性质;能利用对数函数的图像与性质来解决简单问题;2、经过探究对数函数的图像和性质,对数函数与指数函数图像之间的联系,对数函数内部的的联系。培养学生观察问题、分析问题和归纳问题的思维能力以及数学交流能力;渗透类比等基本数学思想方法。3、在学习对数函数过程中,使学生学会认识事物的特殊性与一般性之间的关系,培养数学应用的意识,探索数学。
a.数学抽象:对数函数的性质;b.逻辑推理:对数函数与指数函数的关系;c.数学运算:运用对数函数的性质比较大小;d.直观想象:对数函数的图像;e.数学建模:运用对数函数解决实际问题;
教学重点:掌握对数函数的图像和性质,对数函数与指数函数之间的联系,不同底数的对数函数图
象之间的联系。
教学难点:
对数函数的图像与指数函数的关系;不同底数的对数函数之间的联系。
多媒体
教学过程
设计意图核心教学素养目标
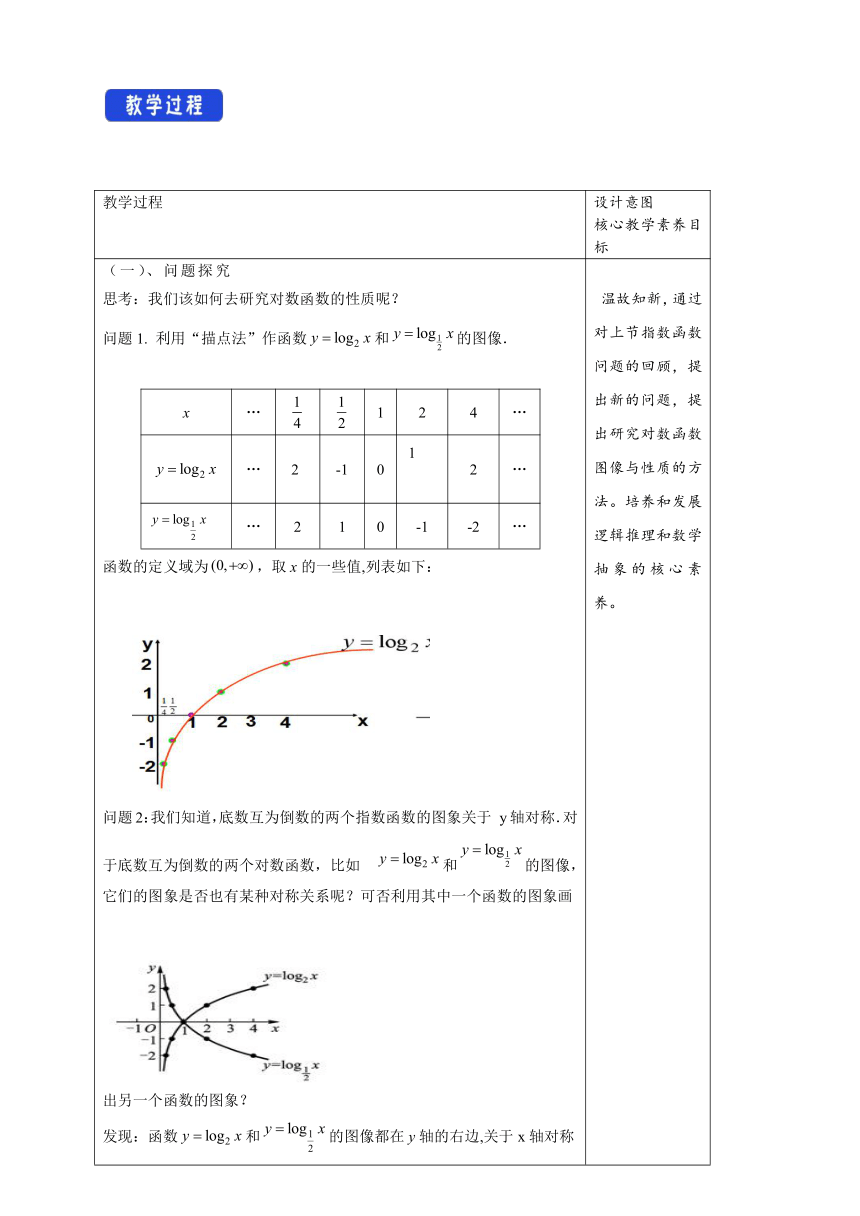
(一)、问题探究思考:我们该如何去研究对数函数的性质呢?问题1.
利用“描点法”作函数和的图像.函数的定义域为,取x的一些值,列表如下:x…124……2[-101[来源:]2……210-1-2…问题2:我们知道,底数互为倒数的两个指数函数的图象关于
y轴对称.对于底数互为倒数的两个对数函数,
比如
和的图像,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?发现:函数和的图像都在y轴的右边,关于x轴对称
问题3:底数a(a>0,且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性由此你能概括出对数函数(a>0,且a≠1)的值域和性质吗?结论1.函数和的图像都在y轴的右边;
2.图像都经过点;3.函数的图像自左至右呈上升趋势;函数的图像自左至右呈下降趋势.观察两幅图象,得到a>1和0函数图象看底数;
底数只能大于0,
等于1来也不行;底数若是大于1,
图象从下往上增;底数0到1之间,
图象从上往下减;无论函数增和减,
图象都过(1,0)点.
(二)、典例解析例1
比较下面两个值的大小⑴
,;⑵
,⑶
,(
a>0
,
a≠1
)解析:(1):用对数函数的单调性,考察函数y=log
2
x
∵a=2
>
1,∴函数在区间(0,+∞)上是增函数;∵3.4<8.5,∴
log23.4<
log28.5(2):考察函数y=log
0.3
x
,
∵a=0.3<
1,
∴函数在区间(0,+∞)上是减函数;∵1.8<2.7
∴
log
0.3
1.8>
log
0.3
2.7
(3):考察函数log
a
5.1与
log
a
5.9
可看作函数y=log
a
x的两个函值
,
对数函数的单调性取决于底数a是大于1还是小于1,因此需要对底数a进行讨论;当a
>
1时,
因为y=log
a
x是增函数,且5.1
<5.9,所以log
a
5.1
<
log
a
5.9
;当0<
a
<
1时,
因为y=log
a
x是减函数,且5.1
<5.9,所以log
a
5.1
>
log
a
5.9
;归纳总结:1.当底数相同时,利用对数函数的单调性比较大小.2.当底数不确定时,要对底数a与1的大小进行分类讨论.跟踪训练1.
比较下列各题中两个值的大小:
⑴
log106
log108
;
⑵
log0.56
log0.54⑶
log0.10.5
log0.10.6;⑷
log1.51.6
log1.51.4答案:<;<;>;>跟踪训练2:已知下列不等式,比较正数m,n
的大小:
(1)
log
3
m
<
log
3
n;
(2)
log
0.3
m
>
log
0.3
n
(3)
log
a
m
<
loga
n
(0(4)
log
a
m
>
log
a
n
(a>1)答案:m
<
n;m
<
n;m
>
n;m
>
n已知函数
y=2x
(x∈R
,y
∈(0,+∞))
可得到x=log2y
,对于任意一个y∈(0,+∞),通过式子x=log2y
,x在R中都有唯一确定的值和它对应。也就是说,可以把y作为自变量,x作为y的函数,这是我们就说x=log2y
(y∈(0,+∞))是函数
y=2x
(
x∈R)
的反函数。
但习惯上,我们通常用x表示自变量,y表示函数。为此我们常常对调函数x=log2y
中的字母x,y,把它写成y=log2x
,这样,对数函数y=log2x
(
x∈(0,+∞)
)是指数函数y=2x
(x∈R
)的反函数。
因此,函数
y
=
logax
(a>0,且a≠1)与指数函数y
=
ax互为反函数。它们的定义域和值域恰好相反。
温故知新,通过对上节指数函数问题的回顾,提出新的问题,提出研究对数函数图像与性质的方法。培养和发展逻辑推理和数学抽象的核心素养。通过画出特殊的对数函数的图形,观察归纳出对数函数的性质,发展学生逻辑推理,数学抽象、数学运算等核心素养;通过典例问题的分析,让学生进一步熟悉对数函数的图像与性质。培养逻辑推理核心素养。运用对数函数的性质解决比较大小问题,发展学生数学运算、逻辑推理的核心素养;通过对应用问题的解决,发展学生数学建模的核心素养;
三、当堂达标1.函数y=logax的图象如图所示,则实数a的可能取值为( )A.5 B.
C.
D.【答案】A [由图可知,a>1,故选A.] 2.当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象为( )
A
B
C
D【答案】:C [(1)∵a>1,∴0<<1,∴y=a-x是减函数,y=logax是增函数,故选C.]3.已知f(x)=loga|x|,满足f(-5)=1,试画出函数f(x)的图象.
解析: ∵f(x)=loga|x|,∴f(-5)=loga5=1,即a=5,∴f(x)=log5|x|,∴f(x)是偶函数,其图象如图所示.4.函数f(x)=loga(2x-5)的图象恒过定点________.【答案】(3,0) [由2x-5=1得x=3,∴f(3)=loga1=0.即函数f(x)恒过定点(3,0).]5.比较下列各组数中两个值的大小:
解:(1)∵log67>log66=1,log76<log77=1,∴log67>log76(2)∵log3π>log31=0,log20.8<log21=0,∴log3π>log20.86:解不等式:
解:原不等式可化为:,
通过练习巩固本节所学知识,巩固对数函数的概念,增强学生的数学抽象、数学运算、逻辑推理的核心素养。
四、小结1.对数函数的图象及性质a的范围01图象定义域(0,+∞)值域R性质定点(1,0),即x=1时,y=0单调性在(0,+∞)上是减函数在(0,+∞)上是增函数2.反函数指数函数y=ax(a>0,且a≠1)和对数函数y=logx(a>0且a≠1)互为反函数.3.思想方法类比:
类比的思想方法;类比指数函数的研究方法;数形结合思想方法是研究函数图像和性质;五、作业1.
课时练
2.
预习下节课内容
学生根据课堂学习,自主总结知识要点,及运用的思想方法。注意总结自己在学习中的易错点;
指数函数与对数函数
4.4.2
对数函数的图像和性质
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.4.2节《对数函数的图像和性质》
是高中数学在指数函数之后的重要初等函数之一。对数函数与指数函数联系密切,无论是研究的思想方法方法还是图像及性质,都有其共通之处。相较于指数函数,对数函数的图象亦有其独特的美感。在类比推理的过程中,感受图像的变化,认识变化的规律,这是提高学生直观想象能力的一个重要的过程。为之后学习数学提供了更多角度的分析方法。培养和发展学生逻辑推理、数学直观、数学抽象、和数学建模的核心素养。
课程目标
学科素养
1、掌握对数函数的图像和性质;能利用对数函数的图像与性质来解决简单问题;2、经过探究对数函数的图像和性质,对数函数与指数函数图像之间的联系,对数函数内部的的联系。培养学生观察问题、分析问题和归纳问题的思维能力以及数学交流能力;渗透类比等基本数学思想方法。3、在学习对数函数过程中,使学生学会认识事物的特殊性与一般性之间的关系,培养数学应用的意识,探索数学。
a.数学抽象:对数函数的性质;b.逻辑推理:对数函数与指数函数的关系;c.数学运算:运用对数函数的性质比较大小;d.直观想象:对数函数的图像;e.数学建模:运用对数函数解决实际问题;
教学重点:掌握对数函数的图像和性质,对数函数与指数函数之间的联系,不同底数的对数函数图
象之间的联系。
教学难点:
对数函数的图像与指数函数的关系;不同底数的对数函数之间的联系。
多媒体
教学过程
设计意图核心教学素养目标
(一)、问题探究思考:我们该如何去研究对数函数的性质呢?问题1.
利用“描点法”作函数和的图像.函数的定义域为,取x的一些值,列表如下:x…124……2[-101[来源:]2……210-1-2…问题2:我们知道,底数互为倒数的两个指数函数的图象关于
y轴对称.对于底数互为倒数的两个对数函数,
比如
和的图像,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?发现:函数和的图像都在y轴的右边,关于x轴对称
问题3:底数a(a>0,且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性由此你能概括出对数函数(a>0,且a≠1)的值域和性质吗?结论1.函数和的图像都在y轴的右边;
2.图像都经过点;3.函数的图像自左至右呈上升趋势;函数的图像自左至右呈下降趋势.观察两幅图象,得到a>1和0
底数只能大于0,
等于1来也不行;底数若是大于1,
图象从下往上增;底数0到1之间,
图象从上往下减;无论函数增和减,
图象都过(1,0)点.
(二)、典例解析例1
比较下面两个值的大小⑴
,;⑵
,⑶
,(
a>0
,
a≠1
)解析:(1):用对数函数的单调性,考察函数y=log
2
x
∵a=2
>
1,∴函数在区间(0,+∞)上是增函数;∵3.4<8.5,∴
log23.4<
log28.5(2):考察函数y=log
0.3
x
,
∵a=0.3<
1,
∴函数在区间(0,+∞)上是减函数;∵1.8<2.7
∴
log
0.3
1.8>
log
0.3
2.7
(3):考察函数log
a
5.1与
log
a
5.9
可看作函数y=log
a
x的两个函值
,
对数函数的单调性取决于底数a是大于1还是小于1,因此需要对底数a进行讨论;当a
>
1时,
因为y=log
a
x是增函数,且5.1
<5.9,所以log
a
5.1
<
log
a
5.9
;当0<
a
<
1时,
因为y=log
a
x是减函数,且5.1
<5.9,所以log
a
5.1
>
log
a
5.9
;归纳总结:1.当底数相同时,利用对数函数的单调性比较大小.2.当底数不确定时,要对底数a与1的大小进行分类讨论.跟踪训练1.
比较下列各题中两个值的大小:
⑴
log106
log108
;
⑵
log0.56
log0.54⑶
log0.10.5
log0.10.6;⑷
log1.51.6
log1.51.4答案:<;<;>;>跟踪训练2:已知下列不等式,比较正数m,n
的大小:
(1)
log
3
m
<
log
3
n;
(2)
log
0.3
m
>
log
0.3
n
(3)
log
a
m
<
loga
n
(0
log
a
m
>
log
a
n
(a>1)答案:m
<
n;m
<
n;m
>
n;m
>
n已知函数
y=2x
(x∈R
,y
∈(0,+∞))
可得到x=log2y
,对于任意一个y∈(0,+∞),通过式子x=log2y
,x在R中都有唯一确定的值和它对应。也就是说,可以把y作为自变量,x作为y的函数,这是我们就说x=log2y
(y∈(0,+∞))是函数
y=2x
(
x∈R)
的反函数。
但习惯上,我们通常用x表示自变量,y表示函数。为此我们常常对调函数x=log2y
中的字母x,y,把它写成y=log2x
,这样,对数函数y=log2x
(
x∈(0,+∞)
)是指数函数y=2x
(x∈R
)的反函数。
因此,函数
y
=
logax
(a>0,且a≠1)与指数函数y
=
ax互为反函数。它们的定义域和值域恰好相反。
温故知新,通过对上节指数函数问题的回顾,提出新的问题,提出研究对数函数图像与性质的方法。培养和发展逻辑推理和数学抽象的核心素养。通过画出特殊的对数函数的图形,观察归纳出对数函数的性质,发展学生逻辑推理,数学抽象、数学运算等核心素养;通过典例问题的分析,让学生进一步熟悉对数函数的图像与性质。培养逻辑推理核心素养。运用对数函数的性质解决比较大小问题,发展学生数学运算、逻辑推理的核心素养;通过对应用问题的解决,发展学生数学建模的核心素养;
三、当堂达标1.函数y=logax的图象如图所示,则实数a的可能取值为( )A.5 B.
C.
D.【答案】A [由图可知,a>1,故选A.] 2.当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象为( )
A
B
C
D【答案】:C [(1)∵a>1,∴0<<1,∴y=a-x是减函数,y=logax是增函数,故选C.]3.已知f(x)=loga|x|,满足f(-5)=1,试画出函数f(x)的图象.
解析: ∵f(x)=loga|x|,∴f(-5)=loga5=1,即a=5,∴f(x)=log5|x|,∴f(x)是偶函数,其图象如图所示.4.函数f(x)=loga(2x-5)的图象恒过定点________.【答案】(3,0) [由2x-5=1得x=3,∴f(3)=loga1=0.即函数f(x)恒过定点(3,0).]5.比较下列各组数中两个值的大小:
解:(1)∵log67>log66=1,log76<log77=1,∴log67>log76(2)∵log3π>log31=0,log20.8<log21=0,∴log3π>log20.86:解不等式:
解:原不等式可化为:,
通过练习巩固本节所学知识,巩固对数函数的概念,增强学生的数学抽象、数学运算、逻辑推理的核心素养。
四、小结1.对数函数的图象及性质a的范围0
类比的思想方法;类比指数函数的研究方法;数形结合思想方法是研究函数图像和性质;五、作业1.
课时练
2.
预习下节课内容
学生根据课堂学习,自主总结知识要点,及运用的思想方法。注意总结自己在学习中的易错点;
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
