勾股定理
图片预览




文档简介
(共23张PPT)
课题:勾股定理
一:实例展示
二:讲授新课
三:定理应用
课 件 制 作: 王 严 生
制 作 单 位: 昆 山 中 学
制 作 时 间: 二零一二年三月二十七日
四:小结与练习
小蜗牛走路
A
B
C
D
蜗牛走了多长的路
小鸟飞行
小鸟飞了多远
8米
2米
8米
飞机的速度有
多少啊???
乙
甲
北
南
西
东
港口
A
B
轮 船 航 海
返回
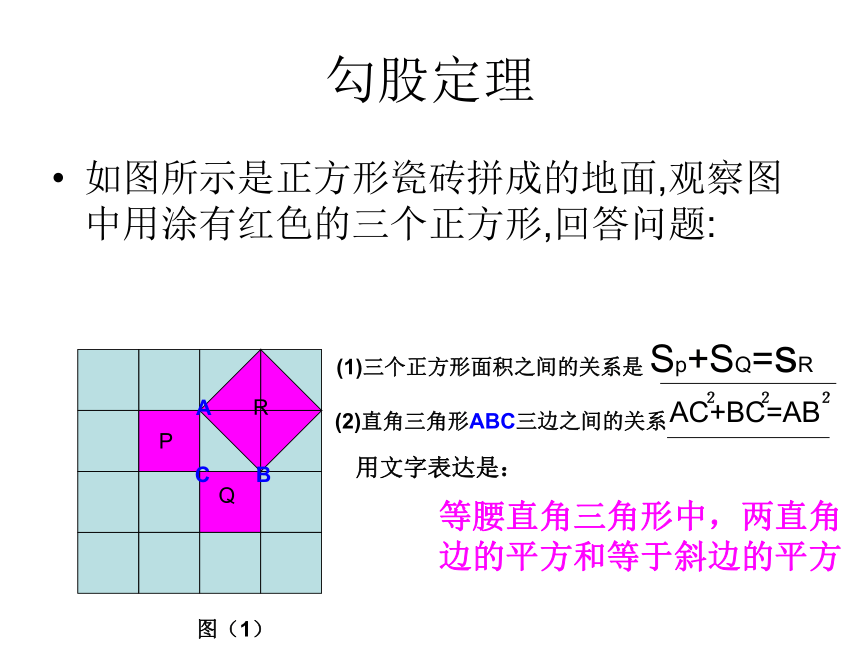
勾股定理
如图所示是正方形瓷砖拼成的地面,观察图中用涂有红色的三个正方形,回答问题:
Q
P
R
(1)三个正方形面积之间的关系是
Sp+SQ=sR
(2)直角三角形ABC三边之间的关系
AC+BC=AB
用文字表达是:
A
B
C
等腰直角三角形中,两直角
边的平方和等于斜边的平方
2
2
2
图(1)
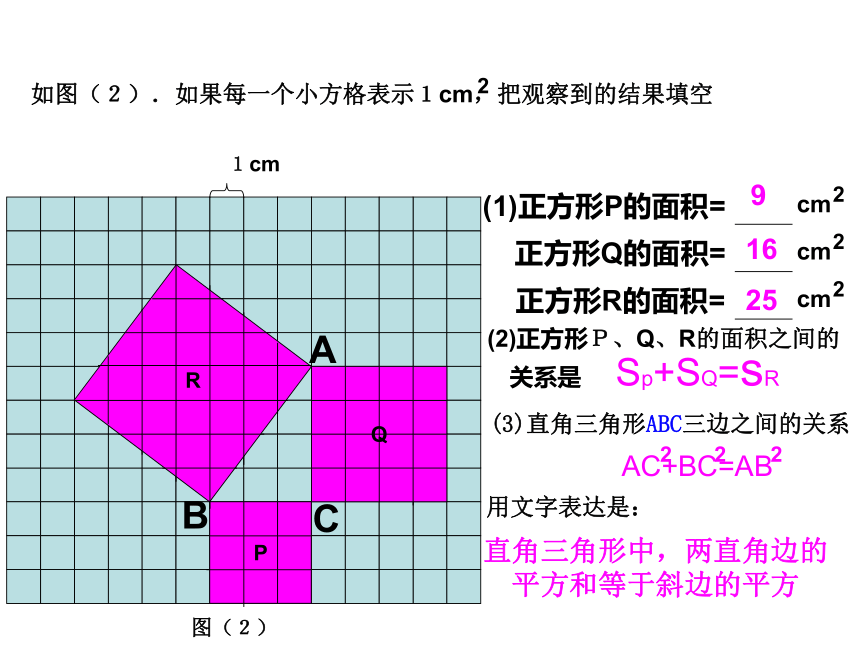
如图(2).如果每一个小方格表示1cm,把观察到的结果填空
图(2)
Sp+SQ=sR
Q
P
R
1cm
2
(1)正方形P的面积=
cm
2
正方形Q的面积=
cm
2
正方形R的面积=
cm
2
(2)正方形P、Q、R的面积之间的
关系是
9
16
25
(3)直角三角形ABC三边之间的关系
用文字表达是:
直角三角形中,两直角边的
平方和等于斜边的平方
AC+BC=AB
2
2
2
A
C
B
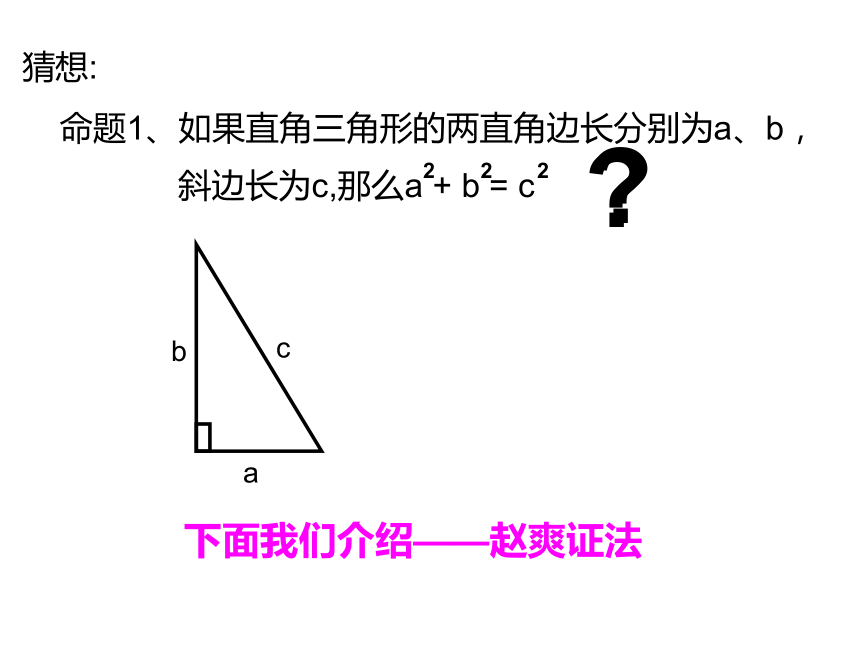
猜想:
命题1、如果直角三角形的两直角边长分别为a、b,
斜边长为c,那么a + b = c
2
2
2
a
c
b
下面我们介绍——赵爽证法
下图是2002年北京国际数学家大会会标,
为什么选它作为这次大会的会标呢?
赵爽弦图
∴a +b =c
a
b
c
(1) 弦图证法
将一个火柴盒侧面ABCD倒下到ABCD的位置,AB=a,BC=b,AC=c利用四边ADBA的面积证明勾股定理.
B
A
D
C
,
,
,
,
,
A
’
D
’
B
,
思考:
a
b
c
(2)美国总统证法:
b
c
a
b
c
a
A
B
C
D
∴a +b =c
定义:
经过被确认正确的命题叫定理。
(也称作勾股定理)
即命题1:如果直角三角形的两直角边长
分别为a、b,
斜边长为c,那么
a + b = c
2
2
2
(2)使用前提是直角三角形
(3)分清直角边、斜边
注意变式: (1) a = c – b a= c – b 等.
2
2
2
2
2
勾
股
弦
A
C
B
a
b
c
勾+股=弦
2
2
2
返回
勾股定理的简单应用
1、如图中的各个直角三角形,求未知边的长。
3
4
A
B
C
?
12
?
13
E
F
G
解:
(1)在直角三角形ABC中
因为AB = AC + BC
所以AB=5
2
2
2
(2)在直角三角形EFG中
因为GF = GE - EF
所以GF=5
2
2
2
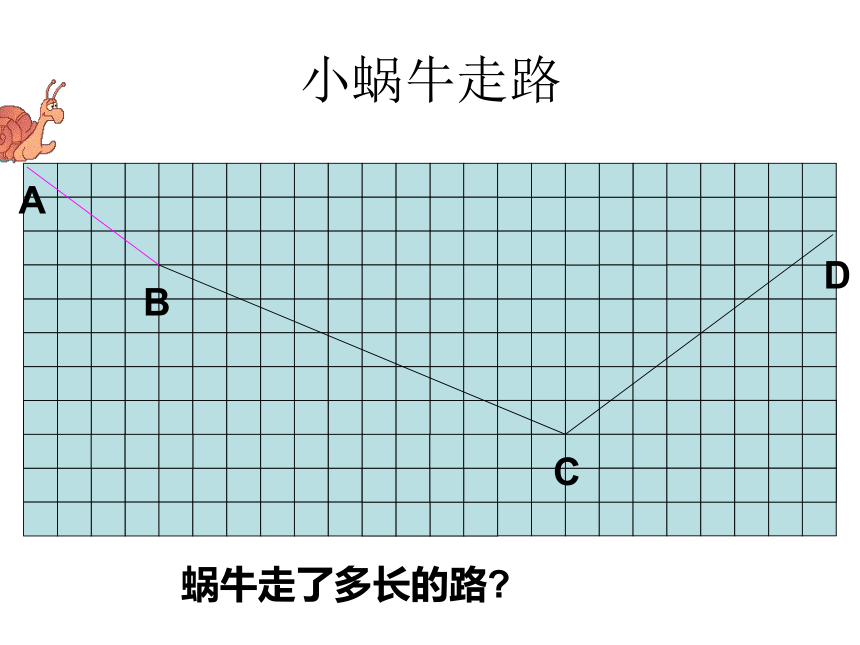
勾股定理的应用一:蜗牛走路
小蜗牛从A点沿图中的折线ABCD到D点,如果
每个小方格的边长是一分米,那么它走了多少米
A
B
C
D
解:由图可知
所以蜗牛走的路为5+13+10=28分米, 即2.8米
AB = 3 + 4 =5
2
2
CD = 6 + 8 =10
2
2
BC = 5 + 12 =13
2
2
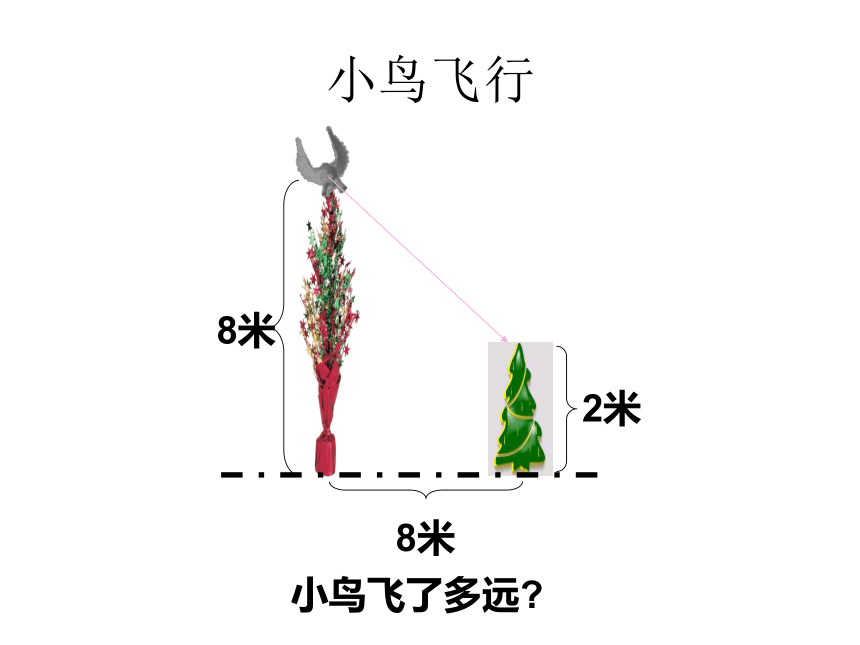
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米
8米
2米
8米
8
2
8
A
B
C
E
. .
.
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米
8
2
8
A
B
C
E
则CE=AD=8m,BE=AB-CD=6m
答:至少飞行10米
解:过点C作CE AB,垂足是E
在直角三角形BEC中,
BC =BE + CE = 6 + 8 =100
2
2
2
2
2
BC = 100=10m
D
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机速度
5000
B
C
4000
A
分析:求BC
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机飞行了多少千米
5000
B
C
4000
A
解:由勾股定理可知
AB = BC + AC
即5000 = BC + 4000
所以BC=3000
飞机飞行了3000米用了20秒
那么它一小时的飞行的距离
是3000 3 60=540000米
即速度是540千米/时
2
2
2
2
2
2
乙
甲
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东北方向航
行,乙船同时以20海里/时速度向东南方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
分析:求AB
A
B
乙
甲
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东南方向航
行,乙船同时以20海里/时速度向东北方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
A
B
解:2小时甲、乙各行的路程是
甲:20 2=40
乙:15 2=30
东南方向与东北方向夹角是90
由勾股定理可知
AB = 40 + 30
AB=50海里
答:它们离开港口2小时后相距
50海里.
2
2
2
返回
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直
角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和,
等于斜边c平方
a2+b2 =c2
⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长.
巩固练习
1、如图,在高为3米,斜坡长为5米的楼梯表面铺
地毯,则地毯长度至少需 米.
2、在三角形ABC中, C=90 AC=4,BC=3
求斜边AB边上的高CD。
A
B
C
D
3、如图:已知AD=14, AB=6, DC=8, BE=EC=y
求AE,ED及y的长。
A
E
D
C
B
6
8
y
y
课题:勾股定理
一:实例展示
二:讲授新课
三:定理应用
课 件 制 作: 王 严 生
制 作 单 位: 昆 山 中 学
制 作 时 间: 二零一二年三月二十七日
四:小结与练习
小蜗牛走路
A
B
C
D
蜗牛走了多长的路
小鸟飞行
小鸟飞了多远
8米
2米
8米
飞机的速度有
多少啊???
乙
甲
北
南
西
东
港口
A
B
轮 船 航 海
返回
勾股定理
如图所示是正方形瓷砖拼成的地面,观察图中用涂有红色的三个正方形,回答问题:
Q
P
R
(1)三个正方形面积之间的关系是
Sp+SQ=sR
(2)直角三角形ABC三边之间的关系
AC+BC=AB
用文字表达是:
A
B
C
等腰直角三角形中,两直角
边的平方和等于斜边的平方
2
2
2
图(1)
如图(2).如果每一个小方格表示1cm,把观察到的结果填空
图(2)
Sp+SQ=sR
Q
P
R
1cm
2
(1)正方形P的面积=
cm
2
正方形Q的面积=
cm
2
正方形R的面积=
cm
2
(2)正方形P、Q、R的面积之间的
关系是
9
16
25
(3)直角三角形ABC三边之间的关系
用文字表达是:
直角三角形中,两直角边的
平方和等于斜边的平方
AC+BC=AB
2
2
2
A
C
B
猜想:
命题1、如果直角三角形的两直角边长分别为a、b,
斜边长为c,那么a + b = c
2
2
2
a
c
b
下面我们介绍——赵爽证法
下图是2002年北京国际数学家大会会标,
为什么选它作为这次大会的会标呢?
赵爽弦图
∴a +b =c
a
b
c
(1) 弦图证法
将一个火柴盒侧面ABCD倒下到ABCD的位置,AB=a,BC=b,AC=c利用四边ADBA的面积证明勾股定理.
B
A
D
C
,
,
,
,
,
A
’
D
’
B
,
思考:
a
b
c
(2)美国总统证法:
b
c
a
b
c
a
A
B
C
D
∴a +b =c
定义:
经过被确认正确的命题叫定理。
(也称作勾股定理)
即命题1:如果直角三角形的两直角边长
分别为a、b,
斜边长为c,那么
a + b = c
2
2
2
(2)使用前提是直角三角形
(3)分清直角边、斜边
注意变式: (1) a = c – b a= c – b 等.
2
2
2
2
2
勾
股
弦
A
C
B
a
b
c
勾+股=弦
2
2
2
返回
勾股定理的简单应用
1、如图中的各个直角三角形,求未知边的长。
3
4
A
B
C
?
12
?
13
E
F
G
解:
(1)在直角三角形ABC中
因为AB = AC + BC
所以AB=5
2
2
2
(2)在直角三角形EFG中
因为GF = GE - EF
所以GF=5
2
2
2
勾股定理的应用一:蜗牛走路
小蜗牛从A点沿图中的折线ABCD到D点,如果
每个小方格的边长是一分米,那么它走了多少米
A
B
C
D
解:由图可知
所以蜗牛走的路为5+13+10=28分米, 即2.8米
AB = 3 + 4 =5
2
2
CD = 6 + 8 =10
2
2
BC = 5 + 12 =13
2
2
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米
8米
2米
8米
8
2
8
A
B
C
E
. .
.
勾股定理的应用二:小鸟飞行
如图.有两棵数,一棵高8米,另一棵高2米,两树相距
8米,一只小鸟从一棵数的梢飞到另一棵树的树梢
求小鸟至少飞了多少米
8
2
8
A
B
C
E
则CE=AD=8m,BE=AB-CD=6m
答:至少飞行10米
解:过点C作CE AB,垂足是E
在直角三角形BEC中,
BC =BE + CE = 6 + 8 =100
2
2
2
2
2
BC = 100=10m
D
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机速度
5000
B
C
4000
A
分析:求BC
勾股定理的应用三:生活实例
3、飞机在空中水平飞行某一时刻刚好飞到一男孩
头顶正上方4000米处,过了20秒,飞机距离这个男孩
头顶5000米,求飞机飞行了多少千米
5000
B
C
4000
A
解:由勾股定理可知
AB = BC + AC
即5000 = BC + 4000
所以BC=3000
飞机飞行了3000米用了20秒
那么它一小时的飞行的距离
是3000 3 60=540000米
即速度是540千米/时
2
2
2
2
2
2
乙
甲
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东北方向航
行,乙船同时以20海里/时速度向东南方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
分析:求AB
A
B
乙
甲
勾股定理的应用四:航海问题
甲轮船以15海里/时的速度从港口向东南方向航
行,乙船同时以20海里/时速度向东北方向航行
求它们离开港口2小时后相距多远?
北
南
西
东
港口
A
B
解:2小时甲、乙各行的路程是
甲:20 2=40
乙:15 2=30
东南方向与东北方向夹角是90
由勾股定理可知
AB = 40 + 30
AB=50海里
答:它们离开港口2小时后相距
50海里.
2
2
2
返回
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直
角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和,
等于斜边c平方
a2+b2 =c2
⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长.
巩固练习
1、如图,在高为3米,斜坡长为5米的楼梯表面铺
地毯,则地毯长度至少需 米.
2、在三角形ABC中, C=90 AC=4,BC=3
求斜边AB边上的高CD。
A
B
C
D
3、如图:已知AD=14, AB=6, DC=8, BE=EC=y
求AE,ED及y的长。
A
E
D
C
B
6
8
y
y
