24.1.2垂直于弦的直径教学课件 2021--2022学年人教版九年级数学上册(15张)
文档属性
| 名称 | 24.1.2垂直于弦的直径教学课件 2021--2022学年人教版九年级数学上册(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
垂直于弦的直径
1.进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质,并能应用它解决一些简单的计算.(重点)
学
习
目
标
自学指导
自学课本81-82页,解决以下问题:
1、圆是轴对称图形吗?如果是,它的对称轴是什么?有多少条对称轴?
2、垂径定理的题设和结论分别是什么?
(3分钟后检查自学效果,如有疑问可以小声问同学或举手问老师)
一、学中感知
圆是轴对称图形,有无数条对称轴,
任何一条直径所在直线都是它的对称轴.
二、导中获知
1、圆的轴对称性
垂径定理的题设和结论分别是什么?
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
题设垂直于弦的直径
结论平分弦,并且平分弦所对的两条弧.
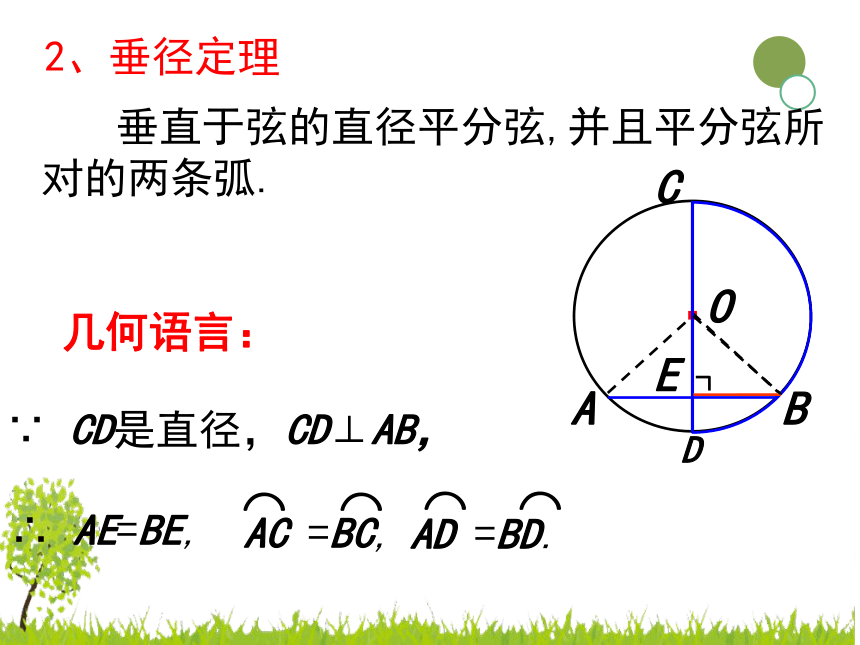
2、垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵
CD是直径,CD⊥AB,
∴
AE=BE,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
几何语言:
·
O
B
E
C
A
D
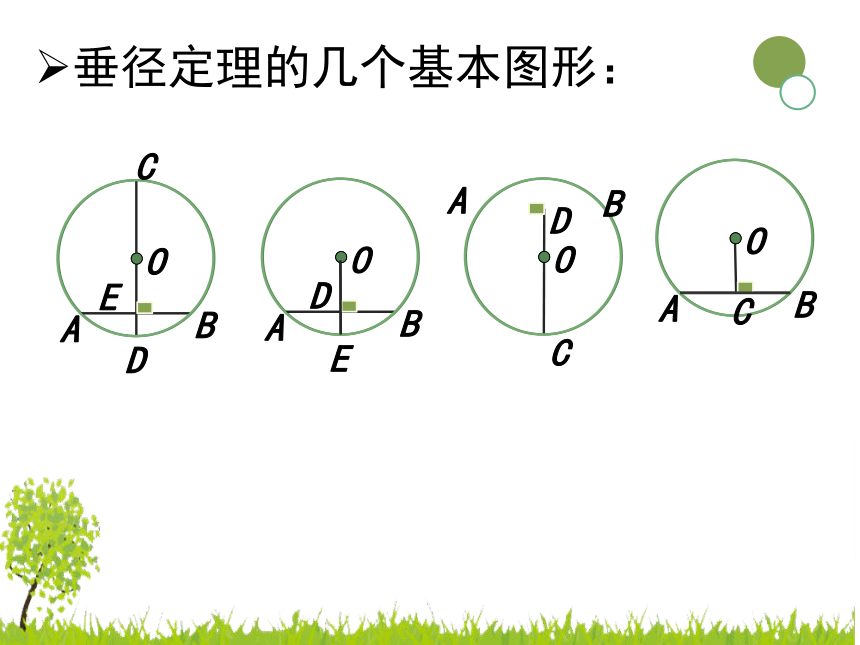
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
例1
如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB=
cm.
·
O
A
B
E
解:连接OA
∴
AB=2AE=16cm.
16
一
∴
cm.
四、练中提能
∵OE⊥AB∴AE=BE
在RtΔAOE中,AO=10cm,OE=6cm
例2
如图,
⊙O的弦AB=8cm
,直径CE⊥AB于D,DC=2cm,求半径OC的长.
·
O
A
B
E
C
D
解:连接OA,∵
直径CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,
根据勾股定理,得
解得
x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
(变式训练)
如图,
⊙O的弦AB=8cm
,直径CE⊥AB于D,ED=8cm,求半径OC的长.
·
O
A
B
E
C
D
解:连接OA,∵
直径CE⊥AB于D,
∴
设OC=xcm,则OD=8-x,
根据勾股定理,得
解得
x=5,
即半径OC的长为5cm.
x2=42+(8-x)2,
方法提炼:
涉及到圆中半径,弦长,弦心距的计算时,
方法:构造________三角形
常作辅助线:
连_______或作弦的___
定理:_____定理和______定理
勾股
垂径
半径
直角
垂线
垂径定理
内容
辅助线
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作垂径
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
五、课堂小结
堂堂清
C
B
课本89页第8题
必做题:
选做题:
1.课本83页第2题
2.课本90页第9题
六、课堂小结
本节课结束
同学们再见
垂直于弦的直径
1.进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质,并能应用它解决一些简单的计算.(重点)
学
习
目
标
自学指导
自学课本81-82页,解决以下问题:
1、圆是轴对称图形吗?如果是,它的对称轴是什么?有多少条对称轴?
2、垂径定理的题设和结论分别是什么?
(3分钟后检查自学效果,如有疑问可以小声问同学或举手问老师)
一、学中感知
圆是轴对称图形,有无数条对称轴,
任何一条直径所在直线都是它的对称轴.
二、导中获知
1、圆的轴对称性
垂径定理的题设和结论分别是什么?
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
题设垂直于弦的直径
结论平分弦,并且平分弦所对的两条弧.
2、垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵
CD是直径,CD⊥AB,
∴
AE=BE,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
几何语言:
·
O
B
E
C
A
D
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
例1
如图,OE⊥AB于E,若⊙O的半径为10cm,OE=6cm,则AB=
cm.
·
O
A
B
E
解:连接OA
∴
AB=2AE=16cm.
16
一
∴
cm.
四、练中提能
∵OE⊥AB∴AE=BE
在RtΔAOE中,AO=10cm,OE=6cm
例2
如图,
⊙O的弦AB=8cm
,直径CE⊥AB于D,DC=2cm,求半径OC的长.
·
O
A
B
E
C
D
解:连接OA,∵
直径CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,
根据勾股定理,得
解得
x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
(变式训练)
如图,
⊙O的弦AB=8cm
,直径CE⊥AB于D,ED=8cm,求半径OC的长.
·
O
A
B
E
C
D
解:连接OA,∵
直径CE⊥AB于D,
∴
设OC=xcm,则OD=8-x,
根据勾股定理,得
解得
x=5,
即半径OC的长为5cm.
x2=42+(8-x)2,
方法提炼:
涉及到圆中半径,弦长,弦心距的计算时,
方法:构造________三角形
常作辅助线:
连_______或作弦的___
定理:_____定理和______定理
勾股
垂径
半径
直角
垂线
垂径定理
内容
辅助线
垂直于弦的直径平分弦,
并且平分弦所对的两条弧
两条辅助线:
连半径,作垂径
构造Rt△利用勾股定理计算或建立方程.
基本图形及变式图形
五、课堂小结
堂堂清
C
B
课本89页第8题
必做题:
选做题:
1.课本83页第2题
2.课本90页第9题
六、课堂小结
本节课结束
同学们再见
同课章节目录
