1.4.1正弦函数、余弦函数的图象课件-2021-2022学年高一下学期数学人教A版必修4(共22张PPT)
文档属性
| 名称 | 1.4.1正弦函数、余弦函数的图象课件-2021-2022学年高一下学期数学人教A版必修4(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
三角函数图象
正弦函数、余弦函数图象
2.一个函数总具有许多基本性质,要直观、全面了解正、余弦函数的基本特性,我们应从哪个方面入手?
1.设实数x对应的角的正弦值为y,则对应关系y=sinx就是一个函数,称为正弦函数;同样y=
cosx也是一个函数,称为余弦函数,这两个函数的定义域是什么?
3.前面我们在学习函数时,先作出函数的图象,再根据函数图象的的特点总结出函数的性质.我们怎样做出正弦函数和余弦函数的图象呢?
新课引入
学习新知
思考1:诱导公式一告诉我们什么结论?
思考2:用描点法作正弦函数y=sinx在[0,2π]内的图象,可取哪些点?
思考3:如何在直角坐标系中比较精确地描出这些点,并画出y=sinx在[0,2π]内的图象?
新课引入
1
-1
0
y
x
●
●
●
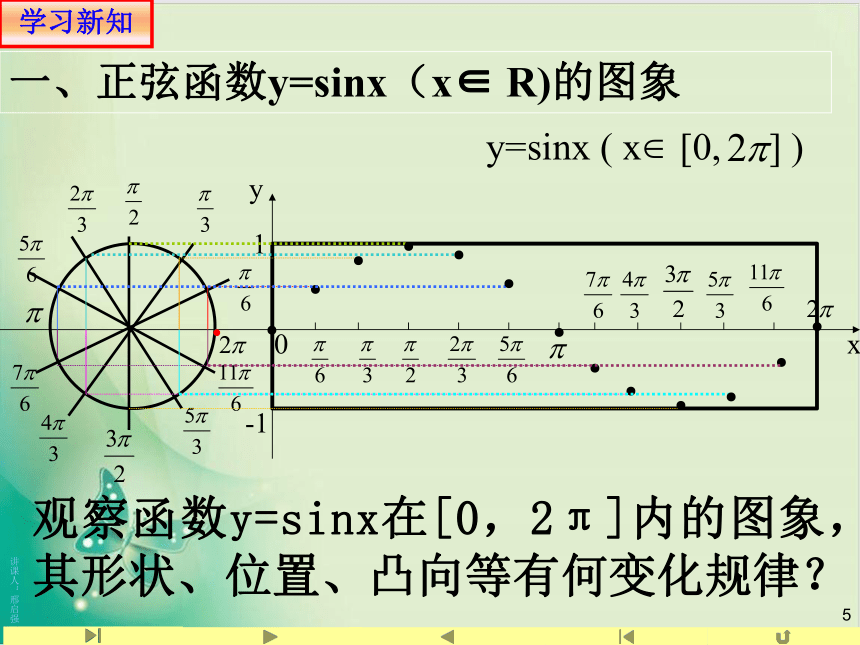
一、正弦函数y=sinx(x∈
R)的图象
y=sinx
(
x
[0,
]
)
●
●
●
●
●
●
●
●
●
●
观察函数y=sinx在[0,2π]内的图象,其形状、位置、凸向等有何变化规律?
学习新知
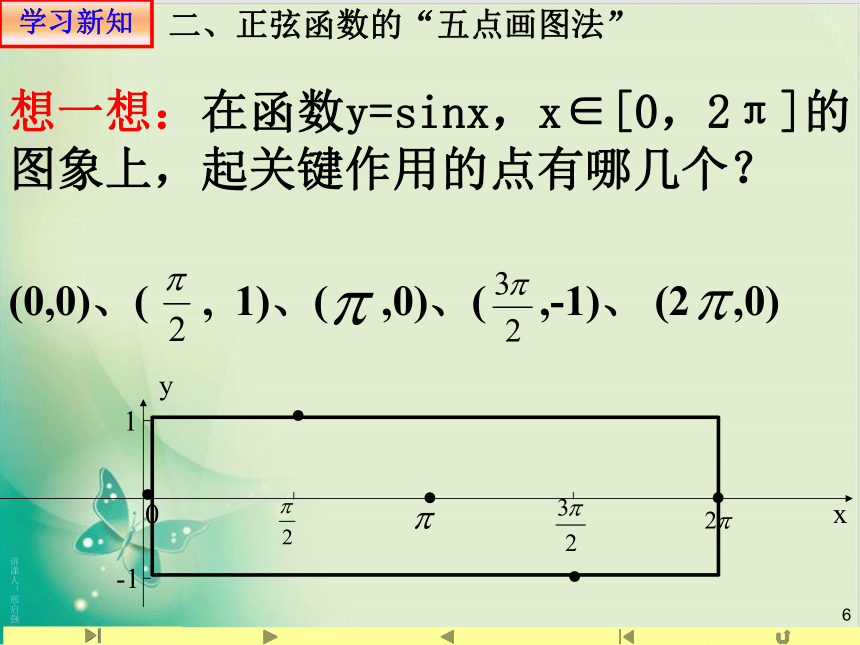
二、正弦函数的“五点画图法”
(0,0)、(
,
1)、(
,0)、(
,-1)、
(2
,0)
0
x
y
1
-1
●
●
●
●
●
想一想:在函数y=sinx,x∈[0,2π]的图象上,起关键作用的点有哪几个?
学习新知
sin(2k
+x)=
(k
Z)
sinx
x
y
0
1
-1
y=sinx
(x
R)
当x∈[2π,4π],
[-2π,0],…时,y=sinx的图象如何?
学习新知
函数y=sinx,x∈R的图象叫做正弦曲线,正弦曲线的分布有什么特点?
y
-1
x
O
1
π
2π
3π
4π
5π
6π
-2π
-3π
-4π
-5π
-6π
-π
你能画出函数y=|sinx|,x∈[0,2π]的图象吗?
y
x
O
π
1
2π
-1
学习新知
是一条“波浪起伏”的连续光滑曲线
一般地,函数y=f(x+a)(a>0)的图象是由函数y=f(x)的图象经过怎样的变换而得到的?
向左平移a个单位.
想一想:设想由正弦函数的图象作出余弦函数的图象,那么先要将余弦函数y=cosx转化为正弦函数,你可以根据哪个公式完成这个转化?
思考4:由诱导公式可知,y=cosx与
是同一个函数,如何作函数
在[0,2π]内的图象?
x
y
O
2π
π
1
y=sinx
-1
思考5:函数y=cosx,x∈[0,2π]的图象如何?其中起关键作用的点有哪几个?
x
y
O
2π
π
1
-1
(0,1)、(
,0)、(
,-1)、(
,0)、(
,
1)
思考6:函数y=cosx,x∈R的图象叫做余弦曲线,怎样画出余弦曲线,余弦曲线的分布有什么特点?
x
y
O
1
-1
例:画出下列函数的简图
(1)y=1+sinx,
x
[0,
]
(2)y=-
cosx,
x
[0,
]
解:(1)按五个关键点列表
x
sinx
1+sinx
0
0
1
0
-1
0
1
2
1
0
1
o
x
y
1
2
●
●
●
●
●
y=1+sinx
x
[0,
]
(1)y=1+sinx,
x
[0,
)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
(2)按五个关键点列表
x
cosx
-cosx
0
1
0
-1
0
1
-1
0
1
0
-1
o
x
y
1
●
●
●
●
●
y=-cosx
x
[0,
]
-1
(2)y=
-cosx,x
[0,
]
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
o
-1
1
2
y=sinx
x
[0,
]
y=1+sinx
x
[0,
]
y
x
y
x
o
-1
1
y=cosx
x
[0,
]
y=-cosx
x
[0,
]
思考
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系?
函数y=-cosx的图象与函数y=cosx的图象有什么关系?
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
例2
当x∈[0,2π]时,求不等式
的解集.
x
y
O
2π
π
1
-1
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
小结:
正弦函数、余弦函数图象的五点法
练习:(1)画出函数y=-sinx
x∈
[0,2π]
(2)画出函数y=1+cosx
x∈
[0,2π]
(3)画出函数y=2sinx
x∈
[0,2π]
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
1
-1
y=
-sinx,
x
[0,
]
1
2
y=1+cosx,
x
[0,
]
(1)
(2)
x
x
y
y
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
(3)
2
1
-1
-2
y
x
y=2sinx,
x
[0,
]
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
小结作业
1.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线.
2.作与正、余弦函数有关的函数图象,是解题的基本要求,用“五点法”作图是常用的方法.
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
3.正、余弦函数的图象不仅是进一步研究函数性质的基础,也是解决有关三角函数问题的工具,这是一种数形结合的数学思想.
作业:P34练习:2
P46习题1.4
A组:
1
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
三角函数图象
正弦函数、余弦函数图象
2.一个函数总具有许多基本性质,要直观、全面了解正、余弦函数的基本特性,我们应从哪个方面入手?
1.设实数x对应的角的正弦值为y,则对应关系y=sinx就是一个函数,称为正弦函数;同样y=
cosx也是一个函数,称为余弦函数,这两个函数的定义域是什么?
3.前面我们在学习函数时,先作出函数的图象,再根据函数图象的的特点总结出函数的性质.我们怎样做出正弦函数和余弦函数的图象呢?
新课引入
学习新知
思考1:诱导公式一告诉我们什么结论?
思考2:用描点法作正弦函数y=sinx在[0,2π]内的图象,可取哪些点?
思考3:如何在直角坐标系中比较精确地描出这些点,并画出y=sinx在[0,2π]内的图象?
新课引入
1
-1
0
y
x
●
●
●
一、正弦函数y=sinx(x∈
R)的图象
y=sinx
(
x
[0,
]
)
●
●
●
●
●
●
●
●
●
●
观察函数y=sinx在[0,2π]内的图象,其形状、位置、凸向等有何变化规律?
学习新知
二、正弦函数的“五点画图法”
(0,0)、(
,
1)、(
,0)、(
,-1)、
(2
,0)
0
x
y
1
-1
●
●
●
●
●
想一想:在函数y=sinx,x∈[0,2π]的图象上,起关键作用的点有哪几个?
学习新知
sin(2k
+x)=
(k
Z)
sinx
x
y
0
1
-1
y=sinx
(x
R)
当x∈[2π,4π],
[-2π,0],…时,y=sinx的图象如何?
学习新知
函数y=sinx,x∈R的图象叫做正弦曲线,正弦曲线的分布有什么特点?
y
-1
x
O
1
π
2π
3π
4π
5π
6π
-2π
-3π
-4π
-5π
-6π
-π
你能画出函数y=|sinx|,x∈[0,2π]的图象吗?
y
x
O
π
1
2π
-1
学习新知
是一条“波浪起伏”的连续光滑曲线
一般地,函数y=f(x+a)(a>0)的图象是由函数y=f(x)的图象经过怎样的变换而得到的?
向左平移a个单位.
想一想:设想由正弦函数的图象作出余弦函数的图象,那么先要将余弦函数y=cosx转化为正弦函数,你可以根据哪个公式完成这个转化?
思考4:由诱导公式可知,y=cosx与
是同一个函数,如何作函数
在[0,2π]内的图象?
x
y
O
2π
π
1
y=sinx
-1
思考5:函数y=cosx,x∈[0,2π]的图象如何?其中起关键作用的点有哪几个?
x
y
O
2π
π
1
-1
(0,1)、(
,0)、(
,-1)、(
,0)、(
,
1)
思考6:函数y=cosx,x∈R的图象叫做余弦曲线,怎样画出余弦曲线,余弦曲线的分布有什么特点?
x
y
O
1
-1
例:画出下列函数的简图
(1)y=1+sinx,
x
[0,
]
(2)y=-
cosx,
x
[0,
]
解:(1)按五个关键点列表
x
sinx
1+sinx
0
0
1
0
-1
0
1
2
1
0
1
o
x
y
1
2
●
●
●
●
●
y=1+sinx
x
[0,
]
(1)y=1+sinx,
x
[0,
)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
(2)按五个关键点列表
x
cosx
-cosx
0
1
0
-1
0
1
-1
0
1
0
-1
o
x
y
1
●
●
●
●
●
y=-cosx
x
[0,
]
-1
(2)y=
-cosx,x
[0,
]
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
o
-1
1
2
y=sinx
x
[0,
]
y=1+sinx
x
[0,
]
y
x
y
x
o
-1
1
y=cosx
x
[0,
]
y=-cosx
x
[0,
]
思考
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系?
函数y=-cosx的图象与函数y=cosx的图象有什么关系?
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
例2
当x∈[0,2π]时,求不等式
的解集.
x
y
O
2π
π
1
-1
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
小结:
正弦函数、余弦函数图象的五点法
练习:(1)画出函数y=-sinx
x∈
[0,2π]
(2)画出函数y=1+cosx
x∈
[0,2π]
(3)画出函数y=2sinx
x∈
[0,2π]
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
1
-1
y=
-sinx,
x
[0,
]
1
2
y=1+cosx,
x
[0,
]
(1)
(2)
x
x
y
y
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
(3)
2
1
-1
-2
y
x
y=2sinx,
x
[0,
]
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
小结作业
1.正、余弦函数的图象每相隔2π个单位重复出现,因此,只要记住它们在[0,2π]内的图象形态,就可以画出正弦曲线和余弦曲线.
2.作与正、余弦函数有关的函数图象,是解题的基本要求,用“五点法”作图是常用的方法.
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
3.正、余弦函数的图象不仅是进一步研究函数性质的基础,也是解决有关三角函数问题的工具,这是一种数形结合的数学思想.
作业:P34练习:2
P46习题1.4
A组:
1
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
山东省滕州市第一中学人教版高中数学新教材必修第一册课件:5.4.1正弦函数、余弦函数的图象(共22张PPT)
