2021-2022学年沪教新版六年级上册数学《第4章 圆和扇形》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年沪教新版六年级上册数学《第4章 圆和扇形》单元测试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览



文档简介
2021-2022学年沪教新版六年级上册数学《第4章
圆和扇形》单元测试卷
一.选择题
1.某校计划在校园内修建一座周长为12米的花坛,同学们设计出正三角形、正方形和圆共三种图案,其中使花坛面积最大的图案是( )
A.正三角形
B.正方形
C.圆
D.不能确定
2.用同样长的三根铁丝分别围成长方形、正方形、圆,其中面积最大的图形是( )
A.长方形
B.正方形
C.圆
D.由于不知道铁丝的长度而无法确定
3.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A.甲先到B点
B.乙先到B点
C.甲、乙同时到B
D.无法确定
4.下列说法中正确的是( )
A.弦是直径
B.弧是半圆
C.半圆是圆中最长的弧
D.直径是圆中最长的弦
5.下列说法错误的是( )
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆叫做等圆
6.如图,圆O的弦中最长的是( )
A.AB
B.CD
C.EF
D.GH
7.下列说法正确的是( )
A.弦是直径
B.弧是半圆
C.直径是圆中最长的弦
D.半圆是圆中最长的弧
8.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条
B.3条
C.4条
D.5条
9.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径
B.等弧的长度一定相等
C.周长相等的两个圆是等圆
D.同一条弦所对的两条弧一定是等弧
10.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
A.π
B.2π
C.3π
D.4π
二.填空题
11.到点A的距离为2cm的所有的点组成的图形是
.
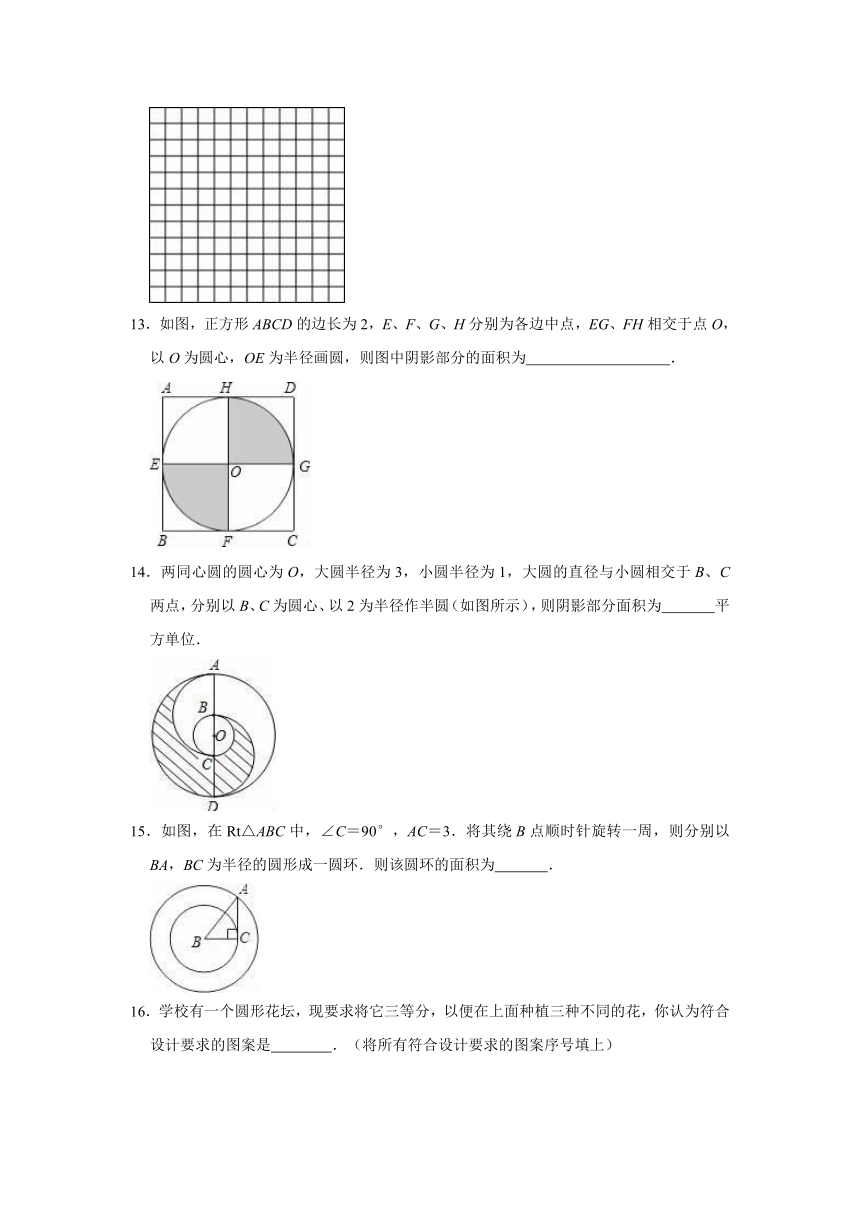
12.请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的
个格点.
13.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为
.
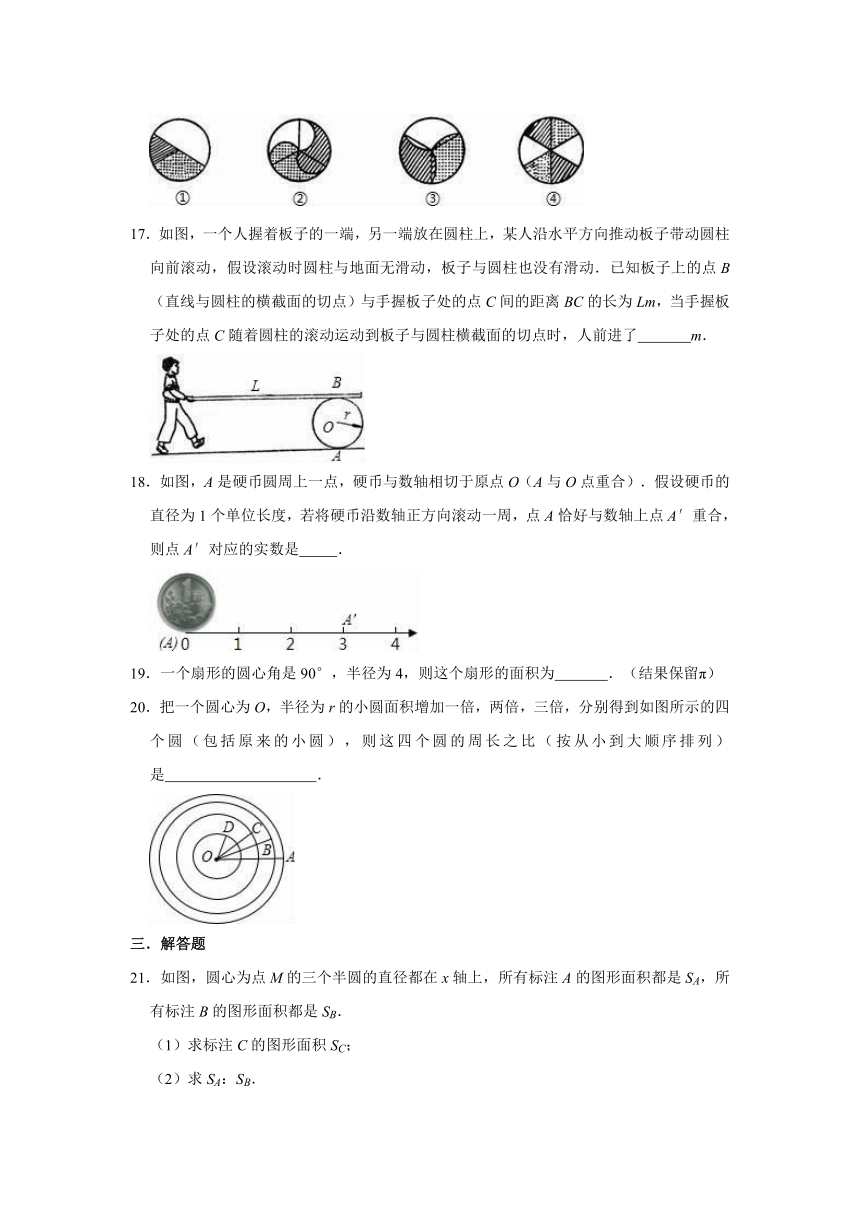
14.两同心圆的圆心为O,大圆半径为3,小圆半径为1,大圆的直径与小圆相交于B、C两点,分别以B、C为圆心、以2为半径作半圆(如图所示),则阴影部分面积为
平方单位.
15.如图,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.则该圆环的面积为
.
16.学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花,你认为符合设计要求的图案是
.(将所有符合设计要求的图案序号填上)
17.如图,一个人握着板子的一端,另一端放在圆柱上,某人沿水平方向推动板子带动圆柱向前滚动,假设滚动时圆柱与地面无滑动,板子与圆柱也没有滑动.已知板子上的点B(直线与圆柱的横截面的切点)与手握板子处的点C间的距离BC的长为Lm,当手握板子处的点C随着圆柱的滚动运动到板子与圆柱横截面的切点时,人前进了
m.
18.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是
.
19.一个扇形的圆心角是90°,半径为4,则这个扇形的面积为
.(结果保留π)
20.把一个圆心为O,半径为r的小圆面积增加一倍,两倍,三倍,分别得到如图所示的四个圆(包括原来的小圆),则这四个圆的周长之比(按从小到大顺序排列)是
.
三.解答题
21.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
22.如图,在△OAB中,OA=OB=2,∠OAE=30°,⊙O切AB于E,且分别交OA、OB于C、D,求图中阴影部分的面积.
23.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
24.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
25.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
参考答案与试题解析
一.选择题
1.解:当设计成正三角形,则边长是4米,则面积是=4平方米;
当设计成正方形时,边长是3米,则面积是9平方米;
当设计成圆时,半径是=米,则面积是π(=平方米.
∵这三个数中最大,
∴使花坛面积最大的图案是圆.
故选:C.
2.解:长方形:设一边为x,S1=x(﹣x)=﹣x2+x,
那么当x=时,S1最大,此时S1=;
正方形:S2=×=;
圆:2πr=L,r=,S3=π?r2=;
∴S3>S2≥S1.
故选:C.
3.解:π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,
因此两个同时到B点.
故选:C.
4.解:A、错误.弦不一定是直径.
B、错误.弧是圆上两点间的部分.
C、错误.优弧大于半圆.
D、正确.直径是圆中最长的弦.
故选:D.
5.解:A、圆有无数条直径,故本选项说法正确;
B、连接圆上任意两点的线段叫弦,故本选项说法正确;
C、过圆心的弦是直径,故本选项说法错误;
D、能够重合的圆全等,则它们是等圆,故本选项说法正确;
故选:C.
6.解:如图所示,圆O的弦中最长的是AB.
故选:A.
7.解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
C、直径是圆中最长的弦,正确,符合题意;
D、半圆是小于优弧而大于劣弧的弧,故错误,不符合题意,
故选:C.
8.解:图中的弦有AB,BC,CE共三条,
故选:B.
9.解:A、过圆心的弦是圆的直径,说法正确;
B、等弧的长度一定相等,说法正确;
C、周长相等的两个圆是等圆,说法正确;
D、同一条弦所对的两条弧一定是等弧,说法错误,应是同一条弦对的两条弧只有在这条弦是直径的情况下是等弧,故原说法错误,符合题意;
故选:D.
10.解:连接OD,BC,
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD,
∵OC∥BD,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,
∴OD=DB,
∴△BOD是等边三角形,
∴∠BOD=60°,
∴∠BOC=60°,
∵DM=CM,
∴S△OBC=S△OBD,
∵OC∥DB,
∴S△OBD=S△CBD,
∴S△OBC=S△DBC,
∴图中阴影部分的面积==2π,
故选:B.
二.填空题
11.解:到点A的距离为2cm的所有的点组成的图形是:以点A为圆心,2cm长为半径的圆.
12.解:如图,画半径为5的圆,可知圆最多能经过169个格点中的12个格点.
故答案为:12.
13.解:由题意可得:OE=1,
阴影面积==.
14.解:∵OA=OD=3,OB=OC=1,
∴AC=BD=4,
∴⊙B和⊙C是等圆,
∴S⊙B=S⊙C,
∴S阴影=S大⊙O﹣S小⊙O=(π×9﹣π×1)=4π.
15.解:圆环的面积=π?AB2﹣π?BC2=π(AB2﹣BC2),在直角△ABC中,根据勾股定理得到AC2=AB2﹣BC2,因而圆环的面积是π?AC2=9π.
16.解:②③④符合要求.
17.解:因为圆向前滚动的距离是Lm,所以人前进了2Lm.
18.解:将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A'重合,则转过的距离是圆的周长是π,因而点A'对应的实数是π.
故答案为:π.
19.解:S扇形==4π,
故答案为:4π.
20.解:设最小的圆的面积是a,则其它三个圆的面积分别是2a,3a,4a,
所有的圆都是相似形,面积的比等于半径的比的平方,
因而半径的比是1:::2,周长的比等于相似比,即半径的比,是1:::2.
故答案为:1:::2.
三.解答题
21.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
22.解:连接OE.
∵⊙O切AB于E,∴OE⊥AB,∴∠OEA=90度.
在Rt△OEA中,∠OAE=30°,OA=2
∴OE=OA=1,∠AOE=60°.
∴AE==.
∵OE⊥AB,OB=OA,
∴BE=2AE=2,∠AOB=2∠OBE=120°.
∴S阴影=S△OAB﹣S扇形OCD=AB?OE﹣=﹣.
23.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
24.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
25.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
圆和扇形》单元测试卷
一.选择题
1.某校计划在校园内修建一座周长为12米的花坛,同学们设计出正三角形、正方形和圆共三种图案,其中使花坛面积最大的图案是( )
A.正三角形
B.正方形
C.圆
D.不能确定
2.用同样长的三根铁丝分别围成长方形、正方形、圆,其中面积最大的图形是( )
A.长方形
B.正方形
C.圆
D.由于不知道铁丝的长度而无法确定
3.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A.甲先到B点
B.乙先到B点
C.甲、乙同时到B
D.无法确定
4.下列说法中正确的是( )
A.弦是直径
B.弧是半圆
C.半圆是圆中最长的弧
D.直径是圆中最长的弦
5.下列说法错误的是( )
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆叫做等圆
6.如图,圆O的弦中最长的是( )
A.AB
B.CD
C.EF
D.GH
7.下列说法正确的是( )
A.弦是直径
B.弧是半圆
C.直径是圆中最长的弦
D.半圆是圆中最长的弧
8.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条
B.3条
C.4条
D.5条
9.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径
B.等弧的长度一定相等
C.周长相等的两个圆是等圆
D.同一条弦所对的两条弧一定是等弧
10.如图,AB是⊙O的直径,弦CD⊥AB,垂足为点M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
A.π
B.2π
C.3π
D.4π
二.填空题
11.到点A的距离为2cm的所有的点组成的图形是
.
12.请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的
个格点.
13.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为
.
14.两同心圆的圆心为O,大圆半径为3,小圆半径为1,大圆的直径与小圆相交于B、C两点,分别以B、C为圆心、以2为半径作半圆(如图所示),则阴影部分面积为
平方单位.
15.如图,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.则该圆环的面积为
.
16.学校有一个圆形花坛,现要求将它三等分,以便在上面种植三种不同的花,你认为符合设计要求的图案是
.(将所有符合设计要求的图案序号填上)
17.如图,一个人握着板子的一端,另一端放在圆柱上,某人沿水平方向推动板子带动圆柱向前滚动,假设滚动时圆柱与地面无滑动,板子与圆柱也没有滑动.已知板子上的点B(直线与圆柱的横截面的切点)与手握板子处的点C间的距离BC的长为Lm,当手握板子处的点C随着圆柱的滚动运动到板子与圆柱横截面的切点时,人前进了
m.
18.如图,A是硬币圆周上一点,硬币与数轴相切于原点O(A与O点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A′重合,则点A′对应的实数是
.
19.一个扇形的圆心角是90°,半径为4,则这个扇形的面积为
.(结果保留π)
20.把一个圆心为O,半径为r的小圆面积增加一倍,两倍,三倍,分别得到如图所示的四个圆(包括原来的小圆),则这四个圆的周长之比(按从小到大顺序排列)是
.
三.解答题
21.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
22.如图,在△OAB中,OA=OB=2,∠OAE=30°,⊙O切AB于E,且分别交OA、OB于C、D,求图中阴影部分的面积.
23.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
24.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
25.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
参考答案与试题解析
一.选择题
1.解:当设计成正三角形,则边长是4米,则面积是=4平方米;
当设计成正方形时,边长是3米,则面积是9平方米;
当设计成圆时,半径是=米,则面积是π(=平方米.
∵这三个数中最大,
∴使花坛面积最大的图案是圆.
故选:C.
2.解:长方形:设一边为x,S1=x(﹣x)=﹣x2+x,
那么当x=时,S1最大,此时S1=;
正方形:S2=×=;
圆:2πr=L,r=,S3=π?r2=;
∴S3>S2≥S1.
故选:C.
3.解:π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,
因此两个同时到B点.
故选:C.
4.解:A、错误.弦不一定是直径.
B、错误.弧是圆上两点间的部分.
C、错误.优弧大于半圆.
D、正确.直径是圆中最长的弦.
故选:D.
5.解:A、圆有无数条直径,故本选项说法正确;
B、连接圆上任意两点的线段叫弦,故本选项说法正确;
C、过圆心的弦是直径,故本选项说法错误;
D、能够重合的圆全等,则它们是等圆,故本选项说法正确;
故选:C.
6.解:如图所示,圆O的弦中最长的是AB.
故选:A.
7.解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
C、直径是圆中最长的弦,正确,符合题意;
D、半圆是小于优弧而大于劣弧的弧,故错误,不符合题意,
故选:C.
8.解:图中的弦有AB,BC,CE共三条,
故选:B.
9.解:A、过圆心的弦是圆的直径,说法正确;
B、等弧的长度一定相等,说法正确;
C、周长相等的两个圆是等圆,说法正确;
D、同一条弦所对的两条弧一定是等弧,说法错误,应是同一条弦对的两条弧只有在这条弦是直径的情况下是等弧,故原说法错误,符合题意;
故选:D.
10.解:连接OD,BC,
∵CD⊥AB,OC=OD,
∴DM=CM,∠COB=∠BOD,
∵OC∥BD,
∴∠COB=∠OBD,
∴∠BOD=∠OBD,
∴OD=DB,
∴△BOD是等边三角形,
∴∠BOD=60°,
∴∠BOC=60°,
∵DM=CM,
∴S△OBC=S△OBD,
∵OC∥DB,
∴S△OBD=S△CBD,
∴S△OBC=S△DBC,
∴图中阴影部分的面积==2π,
故选:B.
二.填空题
11.解:到点A的距离为2cm的所有的点组成的图形是:以点A为圆心,2cm长为半径的圆.
12.解:如图,画半径为5的圆,可知圆最多能经过169个格点中的12个格点.
故答案为:12.
13.解:由题意可得:OE=1,
阴影面积==.
14.解:∵OA=OD=3,OB=OC=1,
∴AC=BD=4,
∴⊙B和⊙C是等圆,
∴S⊙B=S⊙C,
∴S阴影=S大⊙O﹣S小⊙O=(π×9﹣π×1)=4π.
15.解:圆环的面积=π?AB2﹣π?BC2=π(AB2﹣BC2),在直角△ABC中,根据勾股定理得到AC2=AB2﹣BC2,因而圆环的面积是π?AC2=9π.
16.解:②③④符合要求.
17.解:因为圆向前滚动的距离是Lm,所以人前进了2Lm.
18.解:将硬币沿数轴正方向滚动一周,点A恰好与数轴上点A'重合,则转过的距离是圆的周长是π,因而点A'对应的实数是π.
故答案为:π.
19.解:S扇形==4π,
故答案为:4π.
20.解:设最小的圆的面积是a,则其它三个圆的面积分别是2a,3a,4a,
所有的圆都是相似形,面积的比等于半径的比的平方,
因而半径的比是1:::2,周长的比等于相似比,即半径的比,是1:::2.
故答案为:1:::2.
三.解答题
21.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
22.解:连接OE.
∵⊙O切AB于E,∴OE⊥AB,∴∠OEA=90度.
在Rt△OEA中,∠OAE=30°,OA=2
∴OE=OA=1,∠AOE=60°.
∴AE==.
∵OE⊥AB,OB=OA,
∴BE=2AE=2,∠AOB=2∠OBE=120°.
∴S阴影=S△OAB﹣S扇形OCD=AB?OE﹣=﹣.
23.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
24.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
25.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
