2021-2022学年人教版数学八年级上册第十一章推理专练2:与三角形有关的探究 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册第十一章推理专练2:与三角形有关的探究 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 951.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
与三角形计算有关的探究推理
第十一章三角形课件
人教版八年级上册
2
推理
专练
以三角形为基础
以四边形为基础
什么是动点问题?
以运动的点、线段、变化的角、图形的面积为基本条件,
给出一个或多个变量,要求确定变量与其他量之间的函数
等其他关系;或变量在一定条件为定值时,进行相关的计
算和综合解答。
数形结合思想
分类讨论思想
从特殊到一般思想
方程思想
数学思想
动中求静
特殊入手
抓不变量
根据点的运动和图形的变化过程,
对其不同情况分类求解
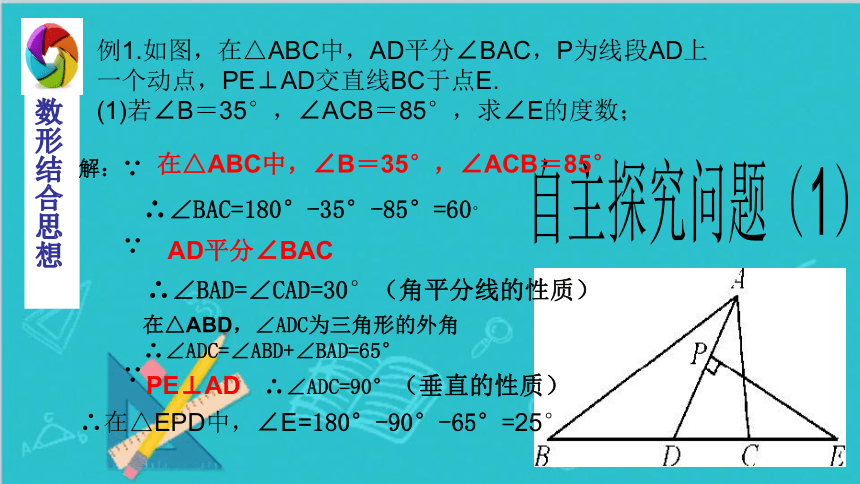
例1.如图,在△ABC中,AD平分∠BAC,P为线段AD上一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
自主探究问题(1)
数形结合思想
在△ABC中,∠B=35°,∠ACB=85°
PE⊥AD
∴∠BAD=∠CAD=30°(角平分线的性质)
AD平分∠BAC
∴∠BAC=180°-35°-85°=60°
∴∠ADC=90°(垂直的性质)
在△ABD,∠ADC为三角形的外角
∴∠ADC=∠ABD+∠BAD=65°
∴在△EPD中,∠E=180°-90°-65°=25°
解:∵
∵
∵
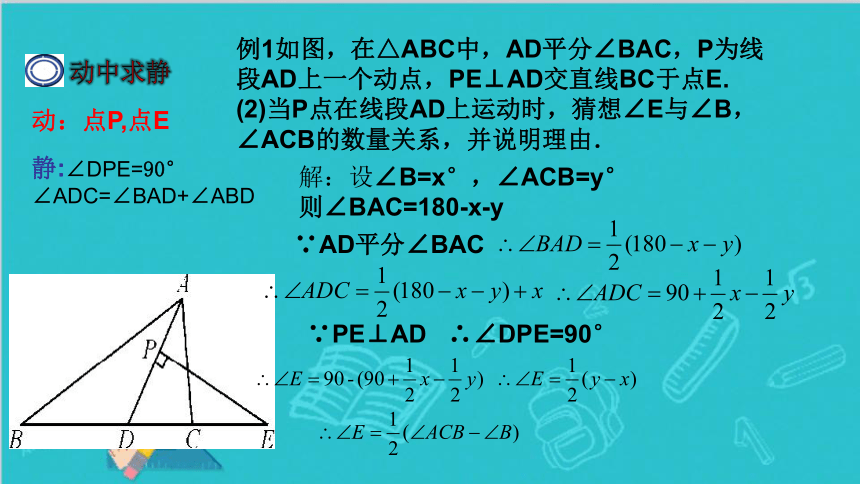
例1如图,在△ABC中,AD平分∠BAC,P为线段AD上一个动点,PE⊥AD交直线BC于点E.
(2)当P点在线段AD上运动时,猜想∠E与∠B,∠ACB的数量关系,并说明理由.
动中求静
动:点P,点E
静:∠DPE=90°
∠ADC=∠BAD+∠ABD
解:设∠B=x°,∠ACB=y°
则∠BAC=180-x-y
∵AD平分∠BAC
∵PE⊥AD
∴∠DPE=90°
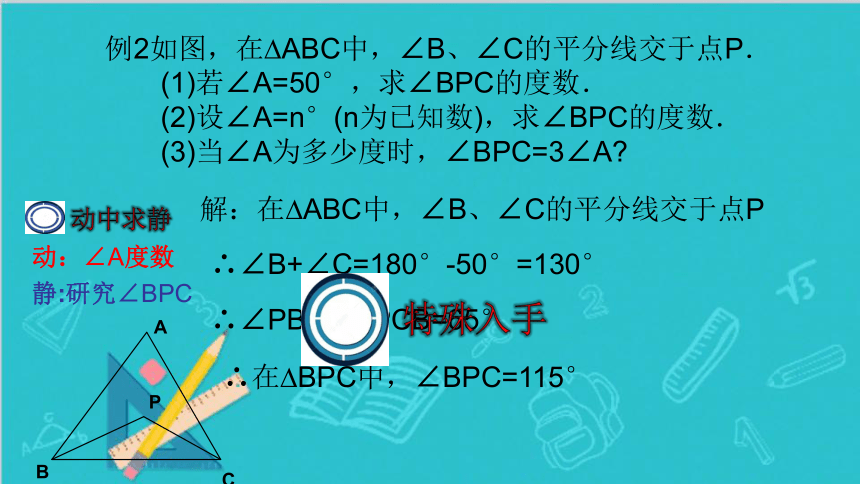
例2如图,在?ABC中,∠B、∠C的平分线交于点P.
(1)若∠A=50°,求∠BPC的度数.
(2)设∠A=n°(n为已知数),求∠BPC的度数.
(3)当∠A为多少度时,∠BPC=3∠A?
动中求静
动:∠A度数
静:研究∠BPC
解:在?ABC中,∠B、∠C的平分线交于点P
∴∠B+∠C=180°-50°=130°
∴∠PBC+∠PCB=65°
∴在?BPC中,∠BPC=115°
特殊入手
例2.如图,在?ABC中,∠B、∠C的平分线交于点P.
(2)设∠A=n°(n为已知数),求∠BPC的度数.
解:在?ABC中,∠B、∠C的平分线交于点P
∴∠B+∠C=180°-n°
∴∠PBC+∠PCB=
方程思想
从特殊到一般思想
例2.如图,在?ABC中,∠B、∠C的平分线交于点P.
(3)当∠A为多少度时,∠BPC=3∠A?
∴∠A=36°
∴即∠A=36°时,∠BPC=3∠A
例3.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,
当∠A=40°时,∠B+∠C+∠1+∠2=______
(3)如图③,是由图①的△ABC沿DE折叠得到的,
如果∠A=30°,则求x+y的值;
猜想∠BDA+∠CEA与∠A的关系为
动中求静
动:图形运动
静:与∠A的关系
解:(1)∠1+∠2=∠B+∠C
∵在△ADE中,∠1+∠2+∠A=180°
∵在△ABC中,∠B+∠C+∠A=180°
∴∠1+∠2=∠B+∠C
自主探究问题(1)
(2)把图①△ABC沿DE折叠,得到图②,
当∠A=40°时,∠B+∠C+∠1+∠2=______
解:(2)∵∠1+∠2=∠B+∠C
∵在△ADE中,∠1+∠2+∠A=180°
∵在△ABC中,∠B+∠C+∠A=180°
∴∠1+∠2+∠B+∠C=140°+140°=280°
自主探究问题(2)
(3)如图③,是由图①的△ABC沿DE折叠得到的,
如果∠A=30°,则求x+y的值;
猜想∠BDA+∠CEA与∠A的关系,并证明
方程思想
解:(3)∵∠1+∠2=∠B+∠C
合作探究问题(3)
∵∠A=30°
∴∠1+∠2=150°
∴x+y=360°-2(∠1+∠2)=∠60°
∠BDA+∠CEA=2∠A
理由如下∵∠1+∠2+∠A=180°
∴2(∠1+∠2+∠A)=360°
又∵2∠1+2∠2+x+y=360°
∴x+y=2∠A
即∠BDA+∠CEA=2∠A
1.如图,在△ABC中,∠1=∠2,∠C>∠B,E为AD上一点,且EF⊥BC于点F.(1)若∠B=40°,∠C=60°,试求∠DEF的度数;
(2)由解答(1)的过程,试探索∠DEF与∠B,∠C的数量关系,并说明理由.
练习:
2.取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转得到△ABC′(如图②),设∠CAC′=α(0°<α<45°).
(1)当α=15°时,求证:AB∥CD;
(2)连接BD,当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC的度数是否变化?若变化,求出变化范围;若不变,求出其度数.
你有什么收获
同学们,再见
与三角形计算有关的探究推理
第十一章三角形课件
人教版八年级上册
2
推理
专练
以三角形为基础
以四边形为基础
什么是动点问题?
以运动的点、线段、变化的角、图形的面积为基本条件,
给出一个或多个变量,要求确定变量与其他量之间的函数
等其他关系;或变量在一定条件为定值时,进行相关的计
算和综合解答。
数形结合思想
分类讨论思想
从特殊到一般思想
方程思想
数学思想
动中求静
特殊入手
抓不变量
根据点的运动和图形的变化过程,
对其不同情况分类求解
例1.如图,在△ABC中,AD平分∠BAC,P为线段AD上一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
自主探究问题(1)
数形结合思想
在△ABC中,∠B=35°,∠ACB=85°
PE⊥AD
∴∠BAD=∠CAD=30°(角平分线的性质)
AD平分∠BAC
∴∠BAC=180°-35°-85°=60°
∴∠ADC=90°(垂直的性质)
在△ABD,∠ADC为三角形的外角
∴∠ADC=∠ABD+∠BAD=65°
∴在△EPD中,∠E=180°-90°-65°=25°
解:∵
∵
∵
例1如图,在△ABC中,AD平分∠BAC,P为线段AD上一个动点,PE⊥AD交直线BC于点E.
(2)当P点在线段AD上运动时,猜想∠E与∠B,∠ACB的数量关系,并说明理由.
动中求静
动:点P,点E
静:∠DPE=90°
∠ADC=∠BAD+∠ABD
解:设∠B=x°,∠ACB=y°
则∠BAC=180-x-y
∵AD平分∠BAC
∵PE⊥AD
∴∠DPE=90°
例2如图,在?ABC中,∠B、∠C的平分线交于点P.
(1)若∠A=50°,求∠BPC的度数.
(2)设∠A=n°(n为已知数),求∠BPC的度数.
(3)当∠A为多少度时,∠BPC=3∠A?
动中求静
动:∠A度数
静:研究∠BPC
解:在?ABC中,∠B、∠C的平分线交于点P
∴∠B+∠C=180°-50°=130°
∴∠PBC+∠PCB=65°
∴在?BPC中,∠BPC=115°
特殊入手
例2.如图,在?ABC中,∠B、∠C的平分线交于点P.
(2)设∠A=n°(n为已知数),求∠BPC的度数.
解:在?ABC中,∠B、∠C的平分线交于点P
∴∠B+∠C=180°-n°
∴∠PBC+∠PCB=
方程思想
从特殊到一般思想
例2.如图,在?ABC中,∠B、∠C的平分线交于点P.
(3)当∠A为多少度时,∠BPC=3∠A?
∴∠A=36°
∴即∠A=36°时,∠BPC=3∠A
例3.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,
当∠A=40°时,∠B+∠C+∠1+∠2=______
(3)如图③,是由图①的△ABC沿DE折叠得到的,
如果∠A=30°,则求x+y的值;
猜想∠BDA+∠CEA与∠A的关系为
动中求静
动:图形运动
静:与∠A的关系
解:(1)∠1+∠2=∠B+∠C
∵在△ADE中,∠1+∠2+∠A=180°
∵在△ABC中,∠B+∠C+∠A=180°
∴∠1+∠2=∠B+∠C
自主探究问题(1)
(2)把图①△ABC沿DE折叠,得到图②,
当∠A=40°时,∠B+∠C+∠1+∠2=______
解:(2)∵∠1+∠2=∠B+∠C
∵在△ADE中,∠1+∠2+∠A=180°
∵在△ABC中,∠B+∠C+∠A=180°
∴∠1+∠2+∠B+∠C=140°+140°=280°
自主探究问题(2)
(3)如图③,是由图①的△ABC沿DE折叠得到的,
如果∠A=30°,则求x+y的值;
猜想∠BDA+∠CEA与∠A的关系,并证明
方程思想
解:(3)∵∠1+∠2=∠B+∠C
合作探究问题(3)
∵∠A=30°
∴∠1+∠2=150°
∴x+y=360°-2(∠1+∠2)=∠60°
∠BDA+∠CEA=2∠A
理由如下∵∠1+∠2+∠A=180°
∴2(∠1+∠2+∠A)=360°
又∵2∠1+2∠2+x+y=360°
∴x+y=2∠A
即∠BDA+∠CEA=2∠A
1.如图,在△ABC中,∠1=∠2,∠C>∠B,E为AD上一点,且EF⊥BC于点F.(1)若∠B=40°,∠C=60°,试求∠DEF的度数;
(2)由解答(1)的过程,试探索∠DEF与∠B,∠C的数量关系,并说明理由.
练习:
2.取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转得到△ABC′(如图②),设∠CAC′=α(0°<α<45°).
(1)当α=15°时,求证:AB∥CD;
(2)连接BD,当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC的度数是否变化?若变化,求出变化范围;若不变,求出其度数.
你有什么收获
同学们,再见
