2021-2022学年人教版数学八年级上册 12.2.6直角三角形全等的应用 推理专练 课件(24张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 12.2.6直角三角形全等的应用 推理专练 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
12.2(6)直角三角形全等的
应用
人教版八年级数学上册
推理专练4
合作探究
直角三角形全等判定定理
典例剖析
回顾
三角形
全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形
全等特有的条件:
HL.
适合所有的三角形
三对等量关系
必须有一组对应边
两对对应边
知识回顾
一对直角相等
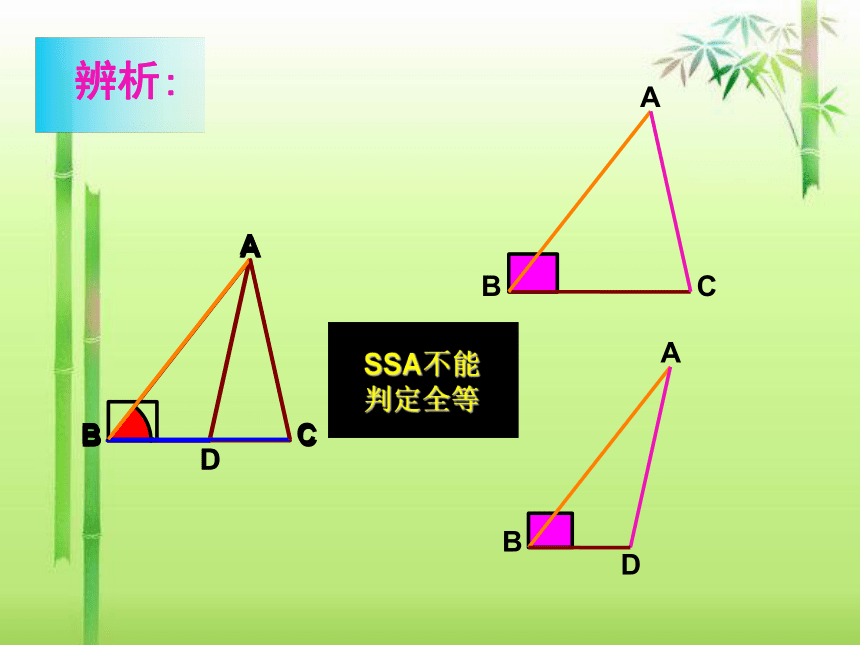
辨析:
A
B
D
A
B
C
SSA不能判定全等
A
B
C
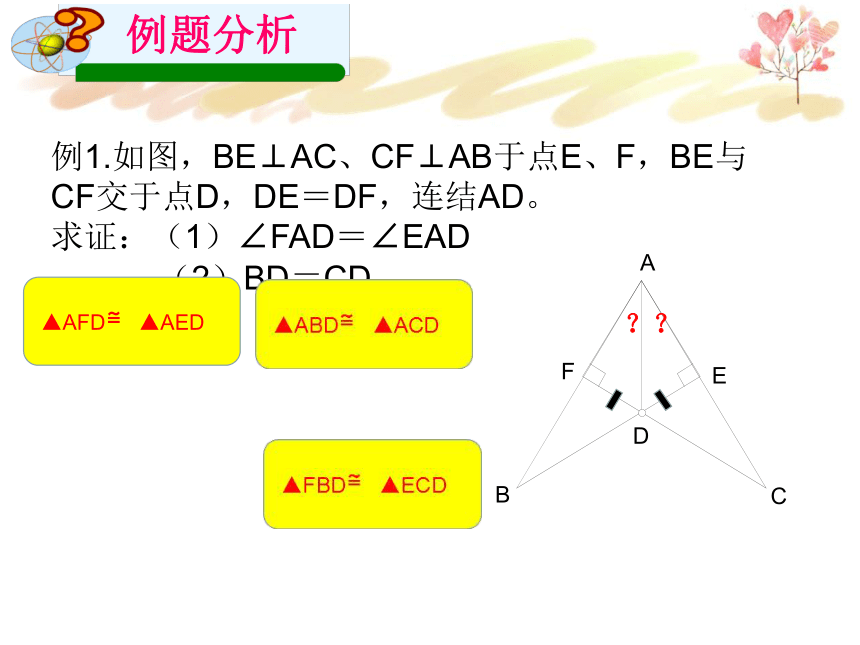
例1.如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,DE=DF,连结AD。
求证:(1)∠FAD=∠EAD
例题分析
?
?
(2)BD=CD
▲AFD≌▲AED
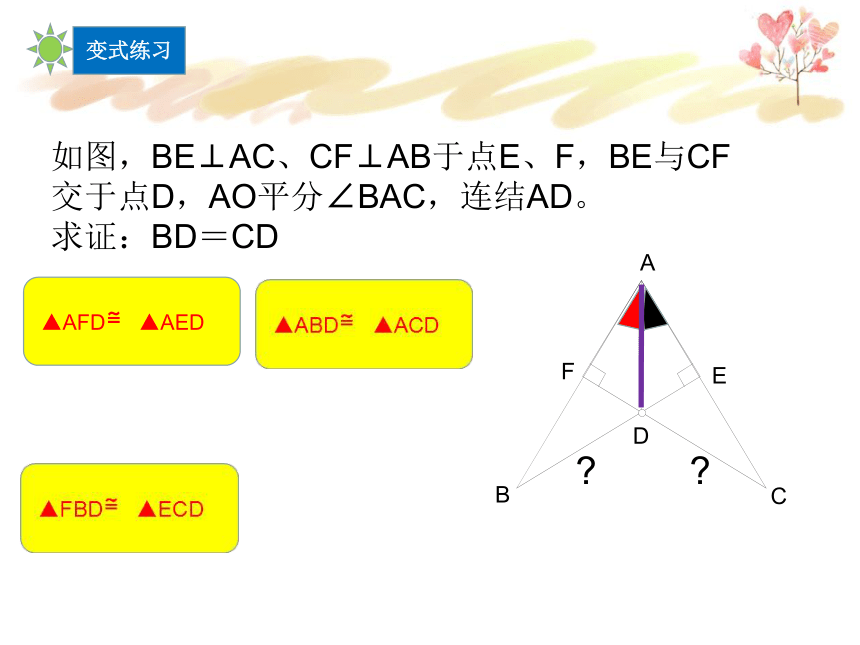
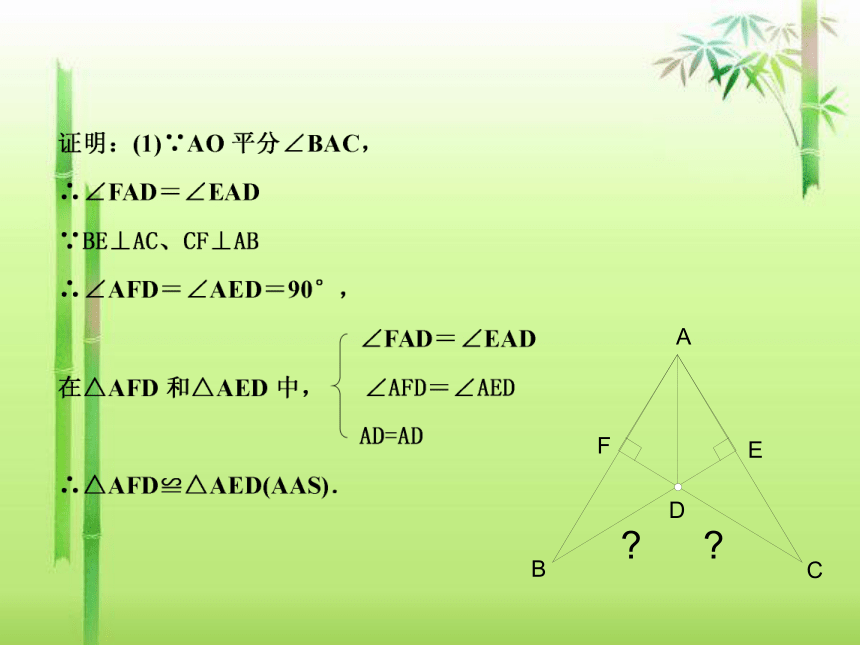
如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,AO平分∠BAC,连结AD。
求证:BD=CD
变式练习
?
?
▲AFD≌▲AED
?
?
?
?
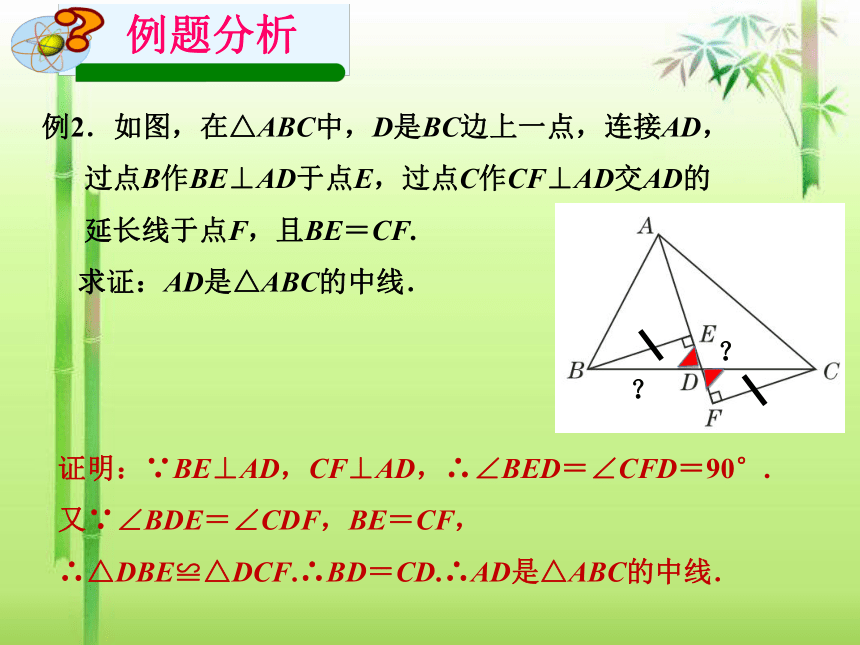
例2.如图,在△ABC中,D是BC边上一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.
求证:AD是△ABC的中线.
证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.
又∵∠BDE=∠CDF,BE=CF,
∴△DBE≌△DCF.∴BD=CD.∴AD是△ABC的中线.
例题分析
?
?
例3已知:如图,△ABC≌△A1B1C1,AD、A1D1分别是△ABC和△A1B1C1的高.
求证:AD=A1D1
证明:∵△ABC≌△A1B1C1(已知)
∴AB=A1B1,∠B=∠B1(全等三角形的对应边、对应角相等)
∵AD、A1D1分别是△ABC、△A1B1C1的高(已知)
∴∠ADB=∠A1D1B1=
90°.
????
在△ABD和△A1B1D1中
∠B=∠B1(已证)
∠ADB=∠A1D1B1(已证)
AB=A1B(已证)
∴△ABD≌△A1B1D1
(AAS)
∴AD=A1D1(全等三角形的对应边相等)
说明:类似的题目还有角平分线相等、中线相等.
1.
如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
合作探究
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
2.如图,在△ABC中,∠ACB=90°,AC=7
cm,BC=3
cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2
cm/s的速度运动,过点E作BC的垂线交直线CD于点F.
(1)求证:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.
?
?
(1)求证:∠A=∠BCD;
(1)证明:由题知∠A+∠ACD=90°,
∠BCD+∠ACD=90°,
∴∠A=∠BCD.
?
?
(2)点E运动多长时间,CF=AB?并说明理由.
?
?
3
7
如图,①当点E在射线BC上运动时,若点E运动5
s,则BE=2×5=10(cm),
∴CE=BE-BC=10-3=7(cm),
∴CE=AC,
在△CFE与△ABC中,
∠CEF=∠ACB=90°,
∠A=∠BCD
CE=AC
∴△CEF≌△ACB,∴CF=AB.
{
E
F
(2)点E运动多长时间,CF=AB?并说明理由.
②当点E在射线CB上运动时,若点E运动2
s,则BE′=2×2=4(cm),
∴CE′=BE′+BC=4+3=7(cm),
∴CE′=AC,
在△CF′E′与△ABC中,
∠E′CF′=∠CAB,∠CF′E′=∠ACB,CE′=AC,
∴△CF′E′≌△ABC,
∴CF′=AB.
综上,当点E在直线CB上运动5
s或2
s时,CF=AB.
3
7
方法总结:
已知直角三角形的直角边(或斜边)相等,
找斜边(或直角边)相等
总结与反思
1.
如图,已知点A,B,C,D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,CE=BF,
求证
AB=CD
巩固与检测
2.如图,AC⊥BC,BD⊥AD,AC=BD,求证:BC=AD.
3.已知:如图AB=AE,∠B=∠E,BC=ED
AF⊥CD
求证:点F是CD的中点
连结AC,AD
1.如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,BD=CD
,连结AD。
求证:AO平分∠BAC
课下作业
2.如图,已知:∠A=90°,
AB=BD,ED⊥BC于
D.
求证:AE=ED
提示:找两个全等三角形,需连结BE.
12.2(6)直角三角形全等的
应用
人教版八年级数学上册
推理专练4
合作探究
直角三角形全等判定定理
典例剖析
回顾
三角形
全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形
全等特有的条件:
HL.
适合所有的三角形
三对等量关系
必须有一组对应边
两对对应边
知识回顾
一对直角相等
辨析:
A
B
D
A
B
C
SSA不能判定全等
A
B
C
例1.如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,DE=DF,连结AD。
求证:(1)∠FAD=∠EAD
例题分析
?
?
(2)BD=CD
▲AFD≌▲AED
如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,AO平分∠BAC,连结AD。
求证:BD=CD
变式练习
?
?
▲AFD≌▲AED
?
?
?
?
例2.如图,在△ABC中,D是BC边上一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.
求证:AD是△ABC的中线.
证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.
又∵∠BDE=∠CDF,BE=CF,
∴△DBE≌△DCF.∴BD=CD.∴AD是△ABC的中线.
例题分析
?
?
例3已知:如图,△ABC≌△A1B1C1,AD、A1D1分别是△ABC和△A1B1C1的高.
求证:AD=A1D1
证明:∵△ABC≌△A1B1C1(已知)
∴AB=A1B1,∠B=∠B1(全等三角形的对应边、对应角相等)
∵AD、A1D1分别是△ABC、△A1B1C1的高(已知)
∴∠ADB=∠A1D1B1=
90°.
????
在△ABD和△A1B1D1中
∠B=∠B1(已证)
∠ADB=∠A1D1B1(已证)
AB=A1B(已证)
∴△ABD≌△A1B1D1
(AAS)
∴AD=A1D1(全等三角形的对应边相等)
说明:类似的题目还有角平分线相等、中线相等.
1.
如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
合作探究
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
2.如图,在△ABC中,∠ACB=90°,AC=7
cm,BC=3
cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2
cm/s的速度运动,过点E作BC的垂线交直线CD于点F.
(1)求证:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.
?
?
(1)求证:∠A=∠BCD;
(1)证明:由题知∠A+∠ACD=90°,
∠BCD+∠ACD=90°,
∴∠A=∠BCD.
?
?
(2)点E运动多长时间,CF=AB?并说明理由.
?
?
3
7
如图,①当点E在射线BC上运动时,若点E运动5
s,则BE=2×5=10(cm),
∴CE=BE-BC=10-3=7(cm),
∴CE=AC,
在△CFE与△ABC中,
∠CEF=∠ACB=90°,
∠A=∠BCD
CE=AC
∴△CEF≌△ACB,∴CF=AB.
{
E
F
(2)点E运动多长时间,CF=AB?并说明理由.
②当点E在射线CB上运动时,若点E运动2
s,则BE′=2×2=4(cm),
∴CE′=BE′+BC=4+3=7(cm),
∴CE′=AC,
在△CF′E′与△ABC中,
∠E′CF′=∠CAB,∠CF′E′=∠ACB,CE′=AC,
∴△CF′E′≌△ABC,
∴CF′=AB.
综上,当点E在直线CB上运动5
s或2
s时,CF=AB.
3
7
方法总结:
已知直角三角形的直角边(或斜边)相等,
找斜边(或直角边)相等
总结与反思
1.
如图,已知点A,B,C,D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,CE=BF,
求证
AB=CD
巩固与检测
2.如图,AC⊥BC,BD⊥AD,AC=BD,求证:BC=AD.
3.已知:如图AB=AE,∠B=∠E,BC=ED
AF⊥CD
求证:点F是CD的中点
连结AC,AD
1.如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,BD=CD
,连结AD。
求证:AO平分∠BAC
课下作业
2.如图,已知:∠A=90°,
AB=BD,ED⊥BC于
D.
求证:AE=ED
提示:找两个全等三角形,需连结BE.
