22.1.1 相似图形与比例线段—沪科版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 22.1.1 相似图形与比例线段—沪科版九年级数学上册课时作业(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 402.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览

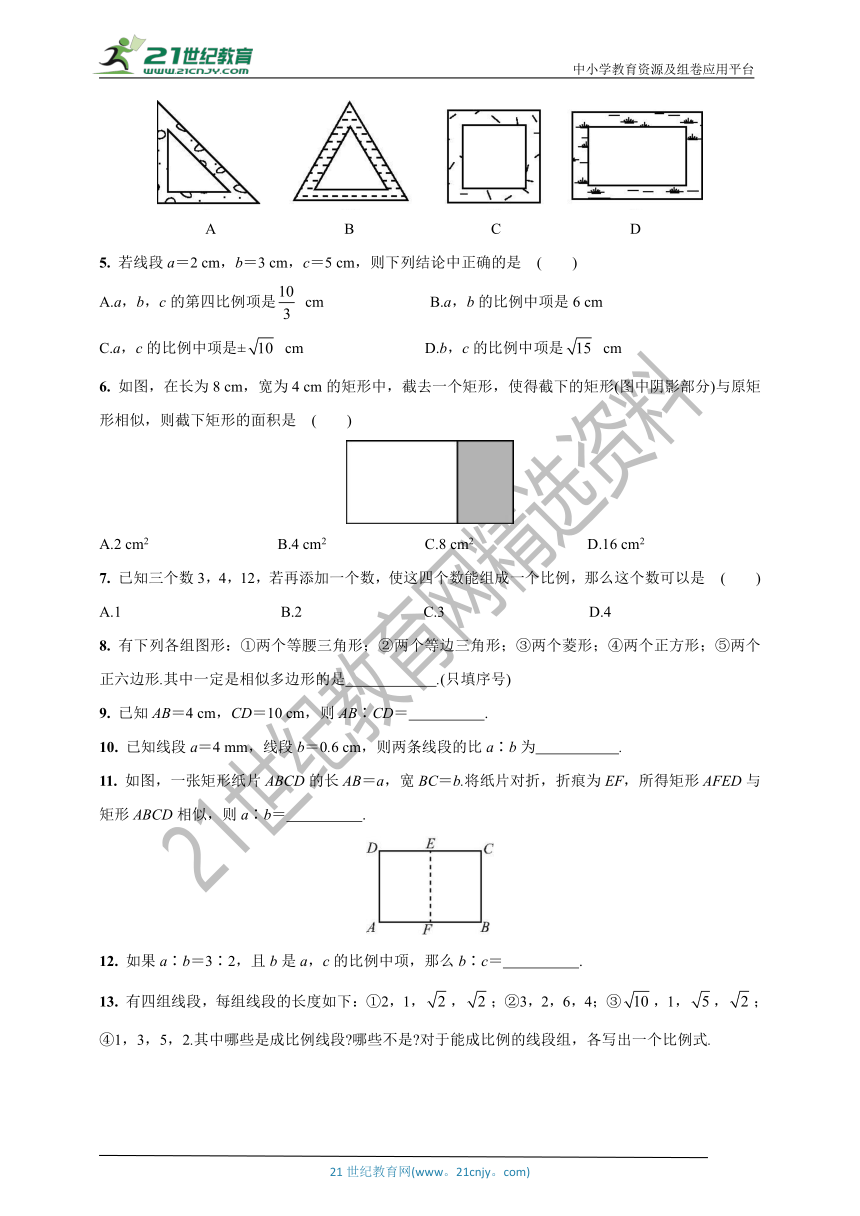
文档简介
中小学教育资源及组卷应用平台
沪科版九年级数学上册课时作业
第22章 相似形
22.1 比例线段
第1课时 相似图形与比例线段
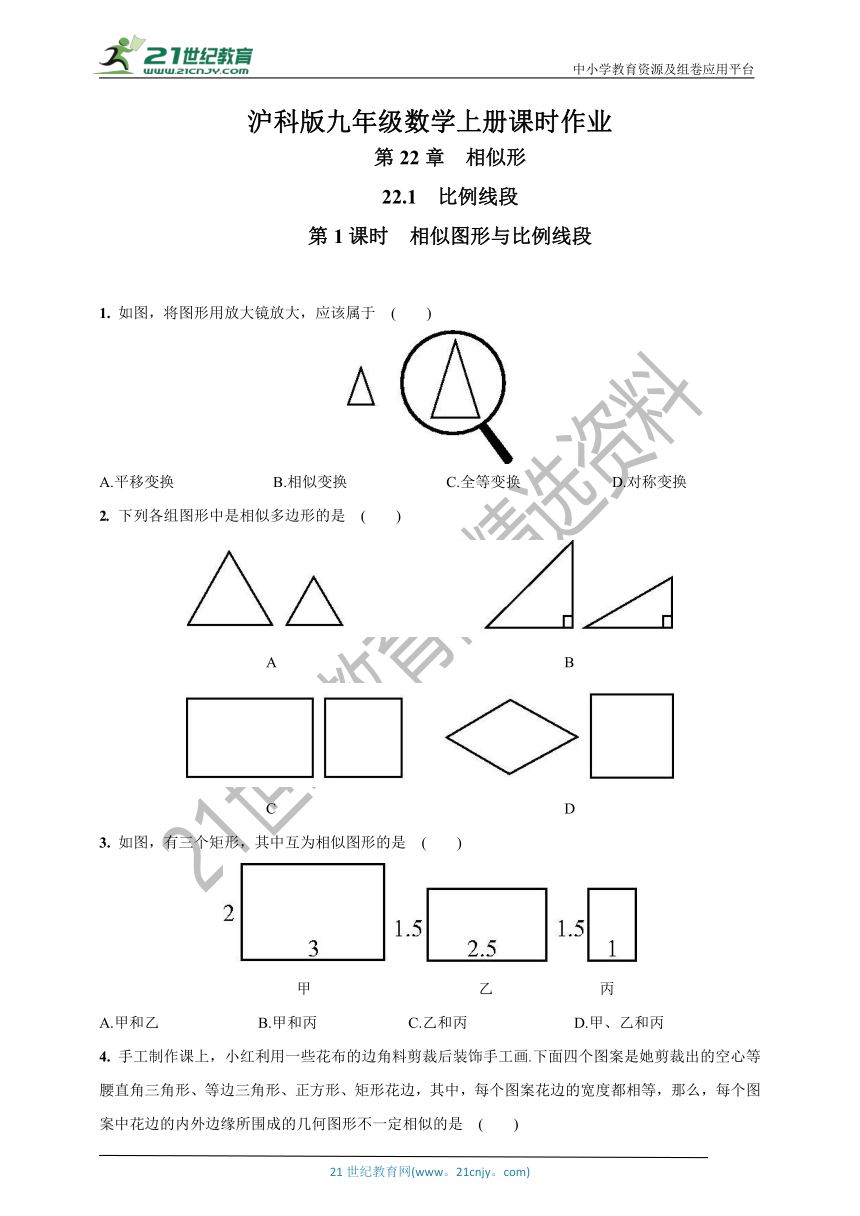
1.
如图,将图形用放大镜放大,应该属于
(
)
A.平移变换
B.相似变换
C.全等变换
D.对称变换
2.
下列各组图形中是相似多边形的是
(
)
A
B
C
D
3.
如图,有三个矩形,其中互为相似图形的是
(
)
甲
乙
丙
A.甲和乙
B.甲和丙
C.乙和丙
D.甲、乙和丙
4.
手工制作课上,小红利用一些花布的边角料剪裁后装饰手工画.下面四个图案是她剪裁出的空心等腰直角三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不一定相似的是
(
)
A
B
C
D
5.
若线段a=2
cm,b=3
cm,c=5
cm,则下列结论中正确的是
(
)
A.a,b,c的第四比例项是
cm
B.a,b的比例中项是6
cm
C.a,c的比例中项是±
cm
D.b,c的比例中项是
cm
6.
如图,在长为8
cm,宽为4
cm的矩形中,截去一个矩形,使得截下的矩形(图中阴影部分)与原矩形相似,则截下矩形的面积是
(
)
A.2
cm2
B.4
cm2
C.8
cm2
D.16
cm2
7.
已知三个数3,4,12,若再添加一个数,使这四个数能组成一个比例,那么这个数可以是
(
)
A.1
B.2
C.3
D.4
8.
有下列各组图形:①两个等腰三角形;②两个等边三角形;③两个菱形;④两个正方形;⑤两个正六边形.其中一定是相似多边形的是
.(只填序号)?
9.
已知AB=4
cm,CD=10
cm,则AB∶CD=
.
10.
已知线段a=4
mm,线段b=0.6
cm,则两条线段的比a∶b为
.?
11.
如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a∶b=
.
12.
如果a∶b=3∶2,且b是a,c的比例中项,那么b∶c=
.
13.
有四组线段,每组线段的长度如下:①2,1,,;②3,2,6,4;③,1,,;④1,3,5,2.其中哪些是成比例线段?哪些不是?对于能成比例的线段组,各写出一个比例式.
14.
如图,C是AB的中点,点D在BC上,AB=24,BD=5,分别求,,的值.
15.
如图,在?ABCD中,AB∥EF.若AB=1,AD=2,AE=AB,则?ABFE与?BCDA相似吗?请说明理由.
16.
已知三条线段的长度分别是4,8,5,试写出另一条线段所有可能的长度,使这四条线段是成比例线段.
17.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高.已知BC=6,AB=10.
(1)求和的值;
(2)再找两条线段和AC,BC构成比例线段(不用说明理由).
参
考
答
案
1.
B
2.
A
3.
B
4.
D
5.
D
6.
C
7.
A
8.
②④⑤
9.
2∶5
10.
2∶3
11.
∶1
12.
3∶2
13.
解:①②③是成比例线段,④不是成比例线段.
①=,②=,③=.
14.
解:由题意可知AC=BC=12,CD=7,BD=5,AD=19,∴=,=,=.
15.
解:相似.理由如下:∵在?ABCD中,AB∥EF,AB=1,AD=2,AE=AB,∴====2.
又∵四边形ABCD是平行四边形,AB∥EF,∴∠A=∠C=∠BFE,∠B=∠D=∠AEF,∴?ABFE与?BCDA相似.
16.
解:设所求的线段长度为x,当x∶4=8∶5时,可得x=;当x∶4=5∶8时,可得x==;当4∶8=5∶x时,可得x==10.
所以所求的线段长度可能为或或10.
17.
解:(1)∵在Rt△ABC中,∠ACB=90°,BC=6,AB=10,∴AC==8,∴==.
又∵在Rt△ABC中,S△ABC=AC·BC=AB·CD,∴CD==4.8,∴==.
(2)CD∶BD=AC∶BC,AD∶CD=AC∶BC.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www。21cnjy。com)
沪科版九年级数学上册课时作业
第22章 相似形
22.1 比例线段
第1课时 相似图形与比例线段
1.
如图,将图形用放大镜放大,应该属于
(
)
A.平移变换
B.相似变换
C.全等变换
D.对称变换
2.
下列各组图形中是相似多边形的是
(
)
A
B
C
D
3.
如图,有三个矩形,其中互为相似图形的是
(
)
甲
乙
丙
A.甲和乙
B.甲和丙
C.乙和丙
D.甲、乙和丙
4.
手工制作课上,小红利用一些花布的边角料剪裁后装饰手工画.下面四个图案是她剪裁出的空心等腰直角三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不一定相似的是
(
)
A
B
C
D
5.
若线段a=2
cm,b=3
cm,c=5
cm,则下列结论中正确的是
(
)
A.a,b,c的第四比例项是
cm
B.a,b的比例中项是6
cm
C.a,c的比例中项是±
cm
D.b,c的比例中项是
cm
6.
如图,在长为8
cm,宽为4
cm的矩形中,截去一个矩形,使得截下的矩形(图中阴影部分)与原矩形相似,则截下矩形的面积是
(
)
A.2
cm2
B.4
cm2
C.8
cm2
D.16
cm2
7.
已知三个数3,4,12,若再添加一个数,使这四个数能组成一个比例,那么这个数可以是
(
)
A.1
B.2
C.3
D.4
8.
有下列各组图形:①两个等腰三角形;②两个等边三角形;③两个菱形;④两个正方形;⑤两个正六边形.其中一定是相似多边形的是
.(只填序号)?
9.
已知AB=4
cm,CD=10
cm,则AB∶CD=
.
10.
已知线段a=4
mm,线段b=0.6
cm,则两条线段的比a∶b为
.?
11.
如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a∶b=
.
12.
如果a∶b=3∶2,且b是a,c的比例中项,那么b∶c=
.
13.
有四组线段,每组线段的长度如下:①2,1,,;②3,2,6,4;③,1,,;④1,3,5,2.其中哪些是成比例线段?哪些不是?对于能成比例的线段组,各写出一个比例式.
14.
如图,C是AB的中点,点D在BC上,AB=24,BD=5,分别求,,的值.
15.
如图,在?ABCD中,AB∥EF.若AB=1,AD=2,AE=AB,则?ABFE与?BCDA相似吗?请说明理由.
16.
已知三条线段的长度分别是4,8,5,试写出另一条线段所有可能的长度,使这四条线段是成比例线段.
17.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高.已知BC=6,AB=10.
(1)求和的值;
(2)再找两条线段和AC,BC构成比例线段(不用说明理由).
参
考
答
案
1.
B
2.
A
3.
B
4.
D
5.
D
6.
C
7.
A
8.
②④⑤
9.
2∶5
10.
2∶3
11.
∶1
12.
3∶2
13.
解:①②③是成比例线段,④不是成比例线段.
①=,②=,③=.
14.
解:由题意可知AC=BC=12,CD=7,BD=5,AD=19,∴=,=,=.
15.
解:相似.理由如下:∵在?ABCD中,AB∥EF,AB=1,AD=2,AE=AB,∴====2.
又∵四边形ABCD是平行四边形,AB∥EF,∴∠A=∠C=∠BFE,∠B=∠D=∠AEF,∴?ABFE与?BCDA相似.
16.
解:设所求的线段长度为x,当x∶4=8∶5时,可得x=;当x∶4=5∶8时,可得x==;当4∶8=5∶x时,可得x==10.
所以所求的线段长度可能为或或10.
17.
解:(1)∵在Rt△ABC中,∠ACB=90°,BC=6,AB=10,∴AC==8,∴==.
又∵在Rt△ABC中,S△ABC=AC·BC=AB·CD,∴CD==4.8,∴==.
(2)CD∶BD=AC∶BC,AD∶CD=AC∶BC.
21世纪教育网
www。21cnjy。com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www。21cnjy。com)
