1.3集合的基本运算 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共26张PPT)
文档属性
| 名称 | 1.3集合的基本运算 课件-2021-2022学年高一上学期数学人教A版(2019)必修第一册(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览





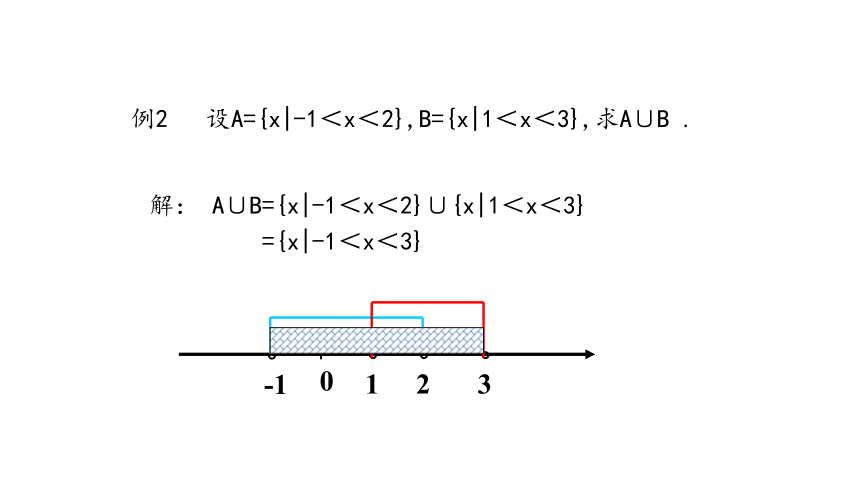

文档简介
(共26张PPT)
集合的基本运算
(一)创设情境
某兴趣小组有20名学生,学号分别是1,2,3,…,20,现新到a,b两本新书,
已知学号是偶数的读过新书a,学号是3的倍数的读过新书b.
(1)
至少读过一本书的学生有2,3,4,6,8,9,10,12,14,15,16,18,20.
(2)
同时读了a,b两本书的学生有6,12,18.
(3)
一本书也没有读的学生有1,5,7,11,13,17,19.
问:
(1)
至少读过一本书的有哪些学生?
(2)
同时读了a,b两本书的有哪些学生?
(3)
一本书也没有读的有哪些学生?
答:
(一)新知导入
2.探索交流
解决问题
【思考1】
设集合A={读过新书a},B={读过新书b},上述问题,与集合A,B的运算有什么联系?
[提示]
两个实数除了可以比较大小外,还可以进行加法运算,类比实数的加法运算,两个集合是否也可以“相加”呢?
?
可以发现,在(1)(2)中的两个集合A和B和C,都具有这样一种
关系:集合C是由所有属于集合A和所有属于集合B的元素组成的。
【思考2】
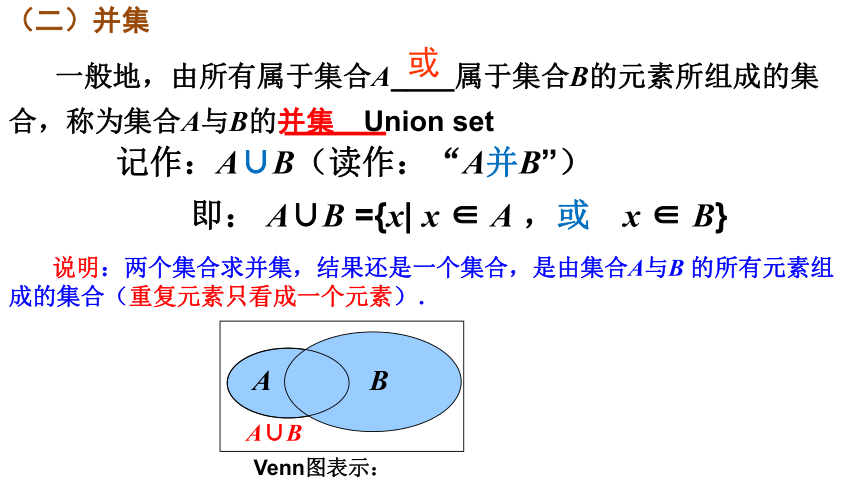
一般地,由所有属于集合A____属于集合B的元素所组成的集合,称为集合A与B的并集(Union
set).
记作:A∪B(读作:“A并B”)
即:
A∪B
={x|
x
∈
A
,或 x
∈
B}
Venn图表示:
A∪B
A
B
说明:两个集合求并集,结果还是一个集合,是由集合A与B
的所有元素组成的集合(重复元素只看成一个元素).
或
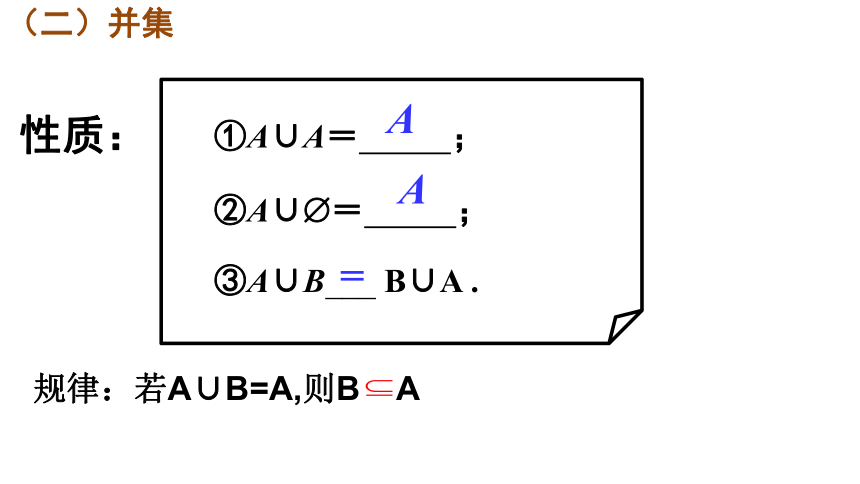
(二)并集
①A∪A=
;
②A∪?=
;
③A∪B___
B∪A
.
A
A
性质:
=
规律:若A∪B=A,则B
A
(二)并集
例1.设A={4,5,6,8},B={3,5,7,8},求
A
U
B.
解:
例2.设集合A={x|-1求AUB.
解:
可以在数轴上表示例2中的并集,如下图:
例2
设A={x|-1<x<2},B={x|1<x<3},求A∪B
.
解:
A∪B={x|-1<x<2}∪{x|1<x<3}
={x|-1<x<3}
。
-1
。
1
。
2
。
3
0
经典例题
例:
已知集合A={x|0≤x≤4},集合B={x|m+1≤x≤1-m},且A∪B=A,求实数m的取值范围.
分析:A∪B=A等价于B?A,
分B=?和B≠?两种情况讨论.
借助于数轴,列出关于m的不等式组,解不等式组得到m的取值范围.
拓展:集合运算的参数问题
经典例题
解:∵A∪B=A,∴B?A.∵A={x|0≤x≤4}≠?,∴B=?或B≠?.
当B=?时,有m+1>1-m,解得m>0.
当B≠?时,用数轴表示集合A和B,如图所示,
综上所得,实数m的取值范围是m>0或-1≤m≤0,即m≥-1.
思考:
求集合的并集是集合间的一种运算,那么,集合间还有其他运算吗?
可以发现,在(1)(2)中,集合C中的元素既属于集合A,又属于集合B,也
就是说集合C是由集合A和B的公共元素组成的集合。
?
一般地,由属于集合A_____属于集合B的所有元素组成的集合,称为A与B的交集(intersection
set).
记作:A∩B(读作:“A交B”)
即:
A
∩
B
={x|
x
∈
A
且x
∈
B}
说明:两个集合求交集,结果还是一个集合,是由集合A与B
的公共元素组成的集合.
且
(三)交集
?
?
?
【解】平面内的两条直线有三种位置关系:①平行;②相交;③重合
?
?
?
A∩A=____,
A∩?=
_______
,
A∩B
____
B∩A.
性质:
A
?
=
规律:若A∩B=A,则A
B
(三)交集
(三)交集
1.(2020北京,1,4分)已知集合A={-1,0,1,2},B={x|0A.{-1,0,1} ????B.{0,1} ????C.{-1,1,2} ????D.{1,2}
解析????集合A与集合B的公共元素为1,2,由交集的定义知A∩B={1,2},故选D.
D
2.已知集合A={x|1 [0,+∞)????.
解析 ①当2m≥1-m,即m≥?时,B=?,符合题意;
②当2m<1-m,即m综上,实数m的取值范围是[0,+∞).
(三)交集
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合全集(Universe
set).通常记作U.
概念
(四)全集
对于一个集合A
,由全集U中不属于集合A的所有元素组成的集合称为集合
A
相对于全集U
的补集(complementary
set),简称为集合A的补集.
Venn图表示:
说明:补集的概念必须要有全集的限制.
记作:
A
即:
A={x|
x
∈
U
且x
A}
A
U
A
(五)补集
例5.
设U={x|x是小于9的正整数}
,
A={1,2,3}
B={3,4,5,6}
,求CUA,CUB
解:∵
U={1,2,3,4,5,6,7,8}
∴
CUA
={4,5,6,7,8}
CUB
={1,2,7,8}
补集例题
Venn图
补集例题
例6.设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.
求A∩B,
(A∪B)
解:根据三角形的分类可知
A∩B=
,
A∪B=
{x|x是锐角三角形或钝角三角形}
(A∪B)={x|x是直角三角形}.
课堂小结
课后习题
4.(2016·全国卷Ⅱ)已知集合A={1,2,3},B={x|(x+1)·(x-2)<0,x∈Z},则A∪B=( )
A.{1}
B.{1,2}
C.{0,1,2,3}
D.{-1,0,1,2,3}
C
解析
因为B={x|(x+1)(x-2)<0,x∈Z}={x|-1求集合并集的2种方法:
(1)定义法:若是用列举法表示的数集,可以根据并集的定义直接观察或用
Venn图表示出集合运算的结果.
(2)数形结合法:若是用描述法表示的数集,可借助数轴分析写出结果,
此时要注意当端点不在集合中时,应用“空心点”表示.
提醒:若两个集合中有相同元素,在求其并集时只能算作一个.
【类题通法】
集合的基本运算
(一)创设情境
某兴趣小组有20名学生,学号分别是1,2,3,…,20,现新到a,b两本新书,
已知学号是偶数的读过新书a,学号是3的倍数的读过新书b.
(1)
至少读过一本书的学生有2,3,4,6,8,9,10,12,14,15,16,18,20.
(2)
同时读了a,b两本书的学生有6,12,18.
(3)
一本书也没有读的学生有1,5,7,11,13,17,19.
问:
(1)
至少读过一本书的有哪些学生?
(2)
同时读了a,b两本书的有哪些学生?
(3)
一本书也没有读的有哪些学生?
答:
(一)新知导入
2.探索交流
解决问题
【思考1】
设集合A={读过新书a},B={读过新书b},上述问题,与集合A,B的运算有什么联系?
[提示]
两个实数除了可以比较大小外,还可以进行加法运算,类比实数的加法运算,两个集合是否也可以“相加”呢?
?
可以发现,在(1)(2)中的两个集合A和B和C,都具有这样一种
关系:集合C是由所有属于集合A和所有属于集合B的元素组成的。
【思考2】
一般地,由所有属于集合A____属于集合B的元素所组成的集合,称为集合A与B的并集(Union
set).
记作:A∪B(读作:“A并B”)
即:
A∪B
={x|
x
∈
A
,或 x
∈
B}
Venn图表示:
A∪B
A
B
说明:两个集合求并集,结果还是一个集合,是由集合A与B
的所有元素组成的集合(重复元素只看成一个元素).
或
(二)并集
①A∪A=
;
②A∪?=
;
③A∪B___
B∪A
.
A
A
性质:
=
规律:若A∪B=A,则B
A
(二)并集
例1.设A={4,5,6,8},B={3,5,7,8},求
A
U
B.
解:
例2.设集合A={x|-1
解:
可以在数轴上表示例2中的并集,如下图:
例2
设A={x|-1<x<2},B={x|1<x<3},求A∪B
.
解:
A∪B={x|-1<x<2}∪{x|1<x<3}
={x|-1<x<3}
。
-1
。
1
。
2
。
3
0
经典例题
例:
已知集合A={x|0≤x≤4},集合B={x|m+1≤x≤1-m},且A∪B=A,求实数m的取值范围.
分析:A∪B=A等价于B?A,
分B=?和B≠?两种情况讨论.
借助于数轴,列出关于m的不等式组,解不等式组得到m的取值范围.
拓展:集合运算的参数问题
经典例题
解:∵A∪B=A,∴B?A.∵A={x|0≤x≤4}≠?,∴B=?或B≠?.
当B=?时,有m+1>1-m,解得m>0.
当B≠?时,用数轴表示集合A和B,如图所示,
综上所得,实数m的取值范围是m>0或-1≤m≤0,即m≥-1.
思考:
求集合的并集是集合间的一种运算,那么,集合间还有其他运算吗?
可以发现,在(1)(2)中,集合C中的元素既属于集合A,又属于集合B,也
就是说集合C是由集合A和B的公共元素组成的集合。
?
一般地,由属于集合A_____属于集合B的所有元素组成的集合,称为A与B的交集(intersection
set).
记作:A∩B(读作:“A交B”)
即:
A
∩
B
={x|
x
∈
A
且x
∈
B}
说明:两个集合求交集,结果还是一个集合,是由集合A与B
的公共元素组成的集合.
且
(三)交集
?
?
?
【解】平面内的两条直线有三种位置关系:①平行;②相交;③重合
?
?
?
A∩A=____,
A∩?=
_______
,
A∩B
____
B∩A.
性质:
A
?
=
规律:若A∩B=A,则A
B
(三)交集
(三)交集
1.(2020北京,1,4分)已知集合A={-1,0,1,2},B={x|0
解析????集合A与集合B的公共元素为1,2,由交集的定义知A∩B={1,2},故选D.
D
2.已知集合A={x|1
解析 ①当2m≥1-m,即m≥?时,B=?,符合题意;
②当2m<1-m,即m综上,实数m的取值范围是[0,+∞).
(三)交集
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合全集(Universe
set).通常记作U.
概念
(四)全集
对于一个集合A
,由全集U中不属于集合A的所有元素组成的集合称为集合
A
相对于全集U
的补集(complementary
set),简称为集合A的补集.
Venn图表示:
说明:补集的概念必须要有全集的限制.
记作:
A
即:
A={x|
x
∈
U
且x
A}
A
U
A
(五)补集
例5.
设U={x|x是小于9的正整数}
,
A={1,2,3}
B={3,4,5,6}
,求CUA,CUB
解:∵
U={1,2,3,4,5,6,7,8}
∴
CUA
={4,5,6,7,8}
CUB
={1,2,7,8}
补集例题
Venn图
补集例题
例6.设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.
求A∩B,
(A∪B)
解:根据三角形的分类可知
A∩B=
,
A∪B=
{x|x是锐角三角形或钝角三角形}
(A∪B)={x|x是直角三角形}.
课堂小结
课后习题
4.(2016·全国卷Ⅱ)已知集合A={1,2,3},B={x|(x+1)·(x-2)<0,x∈Z},则A∪B=( )
A.{1}
B.{1,2}
C.{0,1,2,3}
D.{-1,0,1,2,3}
C
解析
因为B={x|(x+1)(x-2)<0,x∈Z}={x|-1
(1)定义法:若是用列举法表示的数集,可以根据并集的定义直接观察或用
Venn图表示出集合运算的结果.
(2)数形结合法:若是用描述法表示的数集,可借助数轴分析写出结果,
此时要注意当端点不在集合中时,应用“空心点”表示.
提醒:若两个集合中有相同元素,在求其并集时只能算作一个.
【类题通法】
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
