江苏省南京市2022届高三上学期零模考前复习卷(8月)数试题 (Word版含答案)
文档属性
| 名称 | 江苏省南京市2022届高三上学期零模考前复习卷(8月)数试题 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 680.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览



文档简介
南京市2022届高三年级零模考前复习卷
数学
2021.08
第Ⅰ卷(选择题
共60分)
一、单项选择题(本大题共8小题,每题5分,共40分)
1.已知复数,设复数,则的虚部是(
)
A.
B.1
C.
D.
2.已知,为非零实数,则“”是“”的(
)
A.充分而不必要条件
B.必要而不充分条件
C.既不充分也不必要条件
D.充要条件
3.在中,,,,则(
)
A.
B.1
C.2
D.3
4.棱长为的正方体中,点,,分别为棱,,的中点,则过,,三点的平面截正方体所得截面面积为(
)
A.
B.
C.
D.
5.若为锐角,,则(
)
A.
B.
C.
D.
6.将正整数12分解成两个正整数的乘积有,,三种,其中是这三种分解中两数差的绝对值最小的,我们称为12的最佳分解.当是正整数的最佳分解时,我们定义函数,例如,则(
)
A.
B.
C.
D.
7.过点作倾斜角为150°的直线与抛物线:交于两点,,若,则的值为(
)
A.4
B.
C.
D.
8.已知,,且,则下列结论一定正确的是(
)
A.
B.
C.
D.
二、多项选择题(本大题共4小题,每题5分,共20分.每题全选对的得5分,部分选对的得2分,有选错的得0分)
9.已知函数,(,)图象的一条对称轴为,,且在内单调递减,则以下说法正确的是(
)
A.是其中一个对称中心
B.
C.在单增
D.
10.在中,角,,所对的边分别为,,,且,将分别绕边,,所在的直线旋转一周,形成的几何体的体积分别记为,,,侧面积分别记为,,,则(
)
A.
B.
C.
D.
11.设集合,,,,,中至少有两个元素,且,满足:
①对于任意,,若,都有
②对于任意,,若,则;
下列情况中可能出现的有(
)
A.有4个元素,有7个元素
B.有4个元素,有6个元素
C.有3个元素,有5个元素
D.有3个元素,有4个元素
12.甲、乙两人进行围棋比赛,共比赛局,且每局甲获胜的概率和乙获胜的概率均为.如果某人获胜的局数多于另一人,则此人赢得比赛记甲赢得比赛的概率为,则(
)
A.
B.
C.
D.的最大值为
第Ⅱ卷(非选择题
共90分)
三、填空题(本大题共4小题,每题5分,共20分)
13.已知,,则________.
14.根据下面的数据:
1
2
3
4
32
48
72
88
求得关于的回归直线方程为,则这组数据相对于所求的回归直线方程的4个残差的方差为________.(注:残差是指实际观察值与估计值之间的差)
15.斜率为的直线与椭圆:相交于,两点,线段的中点坐标为,则椭圆的离心率等于________.
16.“韩信点兵”问题在我国古代数学史上有不少有趣的名称,如“物不知数”鬼谷算”“隔墙算”“大衍求一术”等,其中《孙子算经》中“物不知数”问题的解法直至1852年传由传教士传入至欧洲,后验证符合由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.原文如下:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”这是一个已知某数被3除余2,被5除余3,被7除余2,求此数的问题.满足条件的数中最小的正整数是________;1至2021这2021个数中满足条件的数的个数是________.
四、解答题(本大题共6小题,共70分)
17.(本题满分10分)
内角,,的对边分别为,,,,.
(1)证明:;
(2)若AC+CB=8,求△ABC的周长.
18.(本题满分12分)
设等差数列的前项和为,已知,且.
(1)求和;
(2)是否存在等差数列,使得对成立?并证明你的结论.
19.(本题满分12分)
为保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏,促进学生身心健康发展,教育部于2021年1月15日下发《关于加强中小学生手机管理工作的通知》,对中小学生的手机使用和管理作出了相关的规定.某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,现对我校80名学生调查得到统计数据如下表,记为事件:“学习成绩优秀且不使用手机”;为事件:“学习成绩不优秀且不使用手机”,且已知事件的频率是事件的频率的2倍.
不使用手机
使用手机
合计
学习成绩优秀人数
12
学习成绩不优秀人数
26
合计
(1)运用独立性检验思想,判断是否有99.5%的把握为中学生使用手机对学习成绩有影响?
(2)采用分层抽样的方法从这80名学生中抽出6名学生,并安排其中3人做书面发言,记做书面发言的成绩优秀的学生数为,求的分布列和数学期望.
参考数据:,其中.
0.10
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
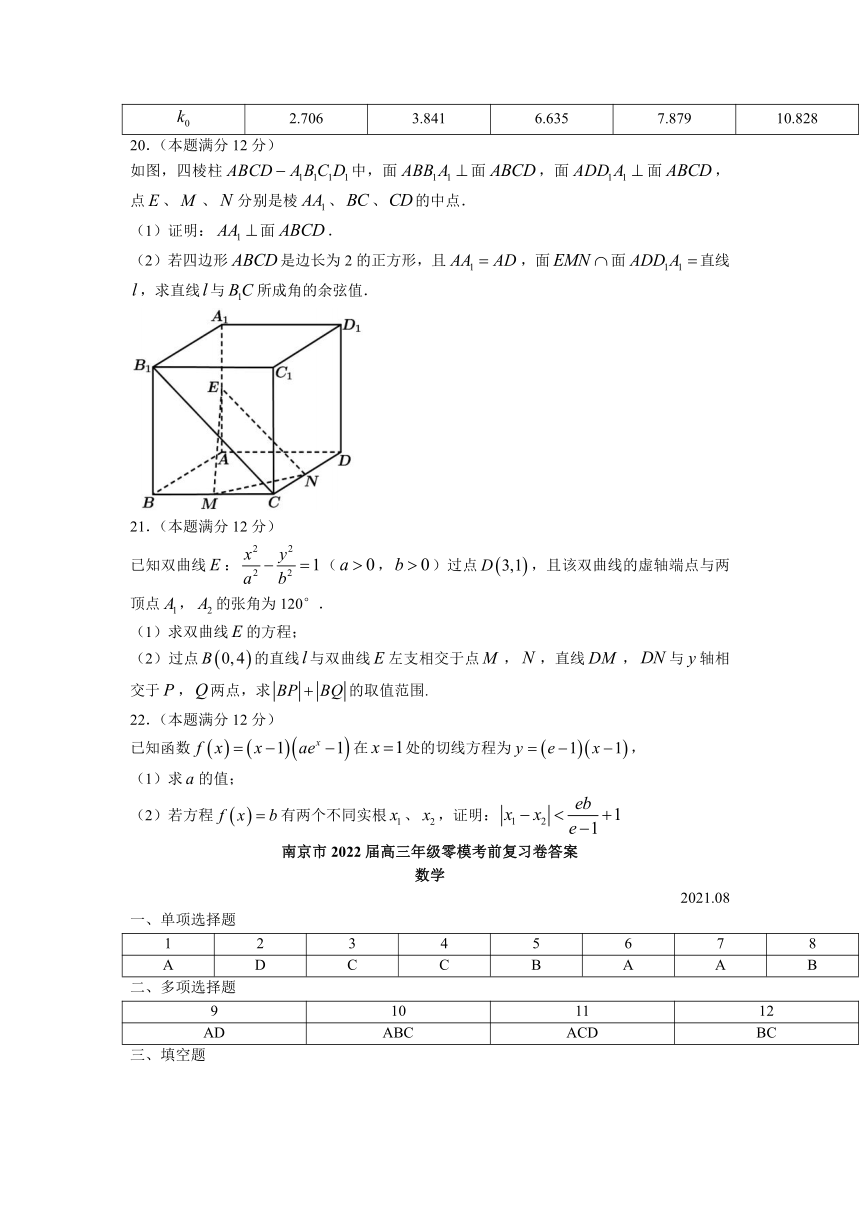
20.(本题满分12分)
如图,四棱柱中,面面,面面,点、、分别是棱、、的中点.
(1)证明:面.
(2)若四边形是边长为2的正方形,且,面面直线,求直线与所成角的余弦值.
21.(本题满分12分)
已知双曲线:(,)过点,且该双曲线的虚轴端点与两顶点,的张角为120°.
(1)求双曲线的方程;
(2)过点的直线与双曲线左支相交于点,,直线,与轴相交于,两点,求的取值范围.
22.(本题满分12分)
已知函数在处的切线方程为,
(1)求的值;
(2)若方程有两个不同实根、,证明:
南京市2022届高三年级零模考前复习卷答案
数学
2021.08
一、单项选择题
1
2
3
4
5
6
7
8
A
D
C
C
B
A
A
B
二、多项选择题
9
10
11
12
AD
ABC
ACD
BC
三、填空题
13.4
14.3.2
15.
16.23,20
四、解答题
17.(1)由,可得,
所以,所以为锐角,,
所以,
由正弦定理可得.
(2)由(1)知,
所以,
设,,,则,解得,
所以的周长为.
18.解:(1)设数列的公差为,则,
解得,,∴,,∴;
(2)设,由可得,
由,可得,
故存在等差数列满足条件,其中,,
下面用数学归纳法证明:当时,对成立,
①当时,由上面过程可知,等式成立,
②假设时等式成立,即,
则当时,
,
,
即当时等式成立,
由①②可知,(其中)对成立.
19.(1)由己知得解得
补全表中所缺数据如下:
不使用手机
使用手机
合计
学习成绩优秀人数
28
12
40
学习成绩不优秀人数
14
26
40
合计
42
38
80
根据题意计算观测值为,
所以有99.5%的把握认为中学生使用手机对学习有影响.
(2)根据题意由分层抽样方法可知,抽取成绩优秀的学生3名,成绩不优秀的学生3名.
从而的所有可能取值为0,1,2,3,
且,,
,,
所以的分布列为
0
1
2
3
的数学期望为.
20.(1)如图所示,在底面中,过点分别作,
因为平面平面面,,且平面,
由面面垂直的性质定理,可得平面,
又由平面,所以,
同理可证:,
又因为,且,平面,所以平面.
(2)因为四边形是边长为2的正方形,且,
可得四棱柱为棱长为2的正方体,
延长交于点,连接,即为平面平面,
则直线与所成角即为直线与所成的角,
取的中点,连接,可得,
则异面直线与所成的角即为与所成的角,设为,其中,
在直角中,可得,
在中,可得,
即直线与所成角的余弦值为
21.(1)由已知∴∴
(2)设直线方程为,,,
直线的方程为,可得
直线的方程为,可得
联立,消去,整理得.
可得
又,所以的范围是.
22.(1)∵,∴,∴;
(2)由(1)得,又,,且
在上单调递增
所以有唯一实根,
时,,递减,时,,递增,
故两根分别在与内,无妨设,
设,,则,
时,,递减,时,,递增,
∴有最小值,即恒成立,,
∴,又因为函数在处的切线方程为,
所以恒成立,
∴,于是.
数学
2021.08
第Ⅰ卷(选择题
共60分)
一、单项选择题(本大题共8小题,每题5分,共40分)
1.已知复数,设复数,则的虚部是(
)
A.
B.1
C.
D.
2.已知,为非零实数,则“”是“”的(
)
A.充分而不必要条件
B.必要而不充分条件
C.既不充分也不必要条件
D.充要条件
3.在中,,,,则(
)
A.
B.1
C.2
D.3
4.棱长为的正方体中,点,,分别为棱,,的中点,则过,,三点的平面截正方体所得截面面积为(
)
A.
B.
C.
D.
5.若为锐角,,则(
)
A.
B.
C.
D.
6.将正整数12分解成两个正整数的乘积有,,三种,其中是这三种分解中两数差的绝对值最小的,我们称为12的最佳分解.当是正整数的最佳分解时,我们定义函数,例如,则(
)
A.
B.
C.
D.
7.过点作倾斜角为150°的直线与抛物线:交于两点,,若,则的值为(
)
A.4
B.
C.
D.
8.已知,,且,则下列结论一定正确的是(
)
A.
B.
C.
D.
二、多项选择题(本大题共4小题,每题5分,共20分.每题全选对的得5分,部分选对的得2分,有选错的得0分)
9.已知函数,(,)图象的一条对称轴为,,且在内单调递减,则以下说法正确的是(
)
A.是其中一个对称中心
B.
C.在单增
D.
10.在中,角,,所对的边分别为,,,且,将分别绕边,,所在的直线旋转一周,形成的几何体的体积分别记为,,,侧面积分别记为,,,则(
)
A.
B.
C.
D.
11.设集合,,,,,中至少有两个元素,且,满足:
①对于任意,,若,都有
②对于任意,,若,则;
下列情况中可能出现的有(
)
A.有4个元素,有7个元素
B.有4个元素,有6个元素
C.有3个元素,有5个元素
D.有3个元素,有4个元素
12.甲、乙两人进行围棋比赛,共比赛局,且每局甲获胜的概率和乙获胜的概率均为.如果某人获胜的局数多于另一人,则此人赢得比赛记甲赢得比赛的概率为,则(
)
A.
B.
C.
D.的最大值为
第Ⅱ卷(非选择题
共90分)
三、填空题(本大题共4小题,每题5分,共20分)
13.已知,,则________.
14.根据下面的数据:
1
2
3
4
32
48
72
88
求得关于的回归直线方程为,则这组数据相对于所求的回归直线方程的4个残差的方差为________.(注:残差是指实际观察值与估计值之间的差)
15.斜率为的直线与椭圆:相交于,两点,线段的中点坐标为,则椭圆的离心率等于________.
16.“韩信点兵”问题在我国古代数学史上有不少有趣的名称,如“物不知数”鬼谷算”“隔墙算”“大衍求一术”等,其中《孙子算经》中“物不知数”问题的解法直至1852年传由传教士传入至欧洲,后验证符合由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.原文如下:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”这是一个已知某数被3除余2,被5除余3,被7除余2,求此数的问题.满足条件的数中最小的正整数是________;1至2021这2021个数中满足条件的数的个数是________.
四、解答题(本大题共6小题,共70分)
17.(本题满分10分)
内角,,的对边分别为,,,,.
(1)证明:;
(2)若AC+CB=8,求△ABC的周长.
18.(本题满分12分)
设等差数列的前项和为,已知,且.
(1)求和;
(2)是否存在等差数列,使得对成立?并证明你的结论.
19.(本题满分12分)
为保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏,促进学生身心健康发展,教育部于2021年1月15日下发《关于加强中小学生手机管理工作的通知》,对中小学生的手机使用和管理作出了相关的规定.某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,现对我校80名学生调查得到统计数据如下表,记为事件:“学习成绩优秀且不使用手机”;为事件:“学习成绩不优秀且不使用手机”,且已知事件的频率是事件的频率的2倍.
不使用手机
使用手机
合计
学习成绩优秀人数
12
学习成绩不优秀人数
26
合计
(1)运用独立性检验思想,判断是否有99.5%的把握为中学生使用手机对学习成绩有影响?
(2)采用分层抽样的方法从这80名学生中抽出6名学生,并安排其中3人做书面发言,记做书面发言的成绩优秀的学生数为,求的分布列和数学期望.
参考数据:,其中.
0.10
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
20.(本题满分12分)
如图,四棱柱中,面面,面面,点、、分别是棱、、的中点.
(1)证明:面.
(2)若四边形是边长为2的正方形,且,面面直线,求直线与所成角的余弦值.
21.(本题满分12分)
已知双曲线:(,)过点,且该双曲线的虚轴端点与两顶点,的张角为120°.
(1)求双曲线的方程;
(2)过点的直线与双曲线左支相交于点,,直线,与轴相交于,两点,求的取值范围.
22.(本题满分12分)
已知函数在处的切线方程为,
(1)求的值;
(2)若方程有两个不同实根、,证明:
南京市2022届高三年级零模考前复习卷答案
数学
2021.08
一、单项选择题
1
2
3
4
5
6
7
8
A
D
C
C
B
A
A
B
二、多项选择题
9
10
11
12
AD
ABC
ACD
BC
三、填空题
13.4
14.3.2
15.
16.23,20
四、解答题
17.(1)由,可得,
所以,所以为锐角,,
所以,
由正弦定理可得.
(2)由(1)知,
所以,
设,,,则,解得,
所以的周长为.
18.解:(1)设数列的公差为,则,
解得,,∴,,∴;
(2)设,由可得,
由,可得,
故存在等差数列满足条件,其中,,
下面用数学归纳法证明:当时,对成立,
①当时,由上面过程可知,等式成立,
②假设时等式成立,即,
则当时,
,
,
即当时等式成立,
由①②可知,(其中)对成立.
19.(1)由己知得解得
补全表中所缺数据如下:
不使用手机
使用手机
合计
学习成绩优秀人数
28
12
40
学习成绩不优秀人数
14
26
40
合计
42
38
80
根据题意计算观测值为,
所以有99.5%的把握认为中学生使用手机对学习有影响.
(2)根据题意由分层抽样方法可知,抽取成绩优秀的学生3名,成绩不优秀的学生3名.
从而的所有可能取值为0,1,2,3,
且,,
,,
所以的分布列为
0
1
2
3
的数学期望为.
20.(1)如图所示,在底面中,过点分别作,
因为平面平面面,,且平面,
由面面垂直的性质定理,可得平面,
又由平面,所以,
同理可证:,
又因为,且,平面,所以平面.
(2)因为四边形是边长为2的正方形,且,
可得四棱柱为棱长为2的正方体,
延长交于点,连接,即为平面平面,
则直线与所成角即为直线与所成的角,
取的中点,连接,可得,
则异面直线与所成的角即为与所成的角,设为,其中,
在直角中,可得,
在中,可得,
即直线与所成角的余弦值为
21.(1)由已知∴∴
(2)设直线方程为,,,
直线的方程为,可得
直线的方程为,可得
联立,消去,整理得.
可得
又,所以的范围是.
22.(1)∵,∴,∴;
(2)由(1)得,又,,且
在上单调递增
所以有唯一实根,
时,,递减,时,,递增,
故两根分别在与内,无妨设,
设,,则,
时,,递减,时,,递增,
∴有最小值,即恒成立,,
∴,又因为函数在处的切线方程为,
所以恒成立,
∴,于是.
同课章节目录
