2020-2021学年山东省潍坊市八年级(下)期末数学试卷(Word版含解析)
文档属性
| 名称 | 2020-2021学年山东省潍坊市八年级(下)期末数学试卷(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 10:44:12 | ||
图片预览




文档简介
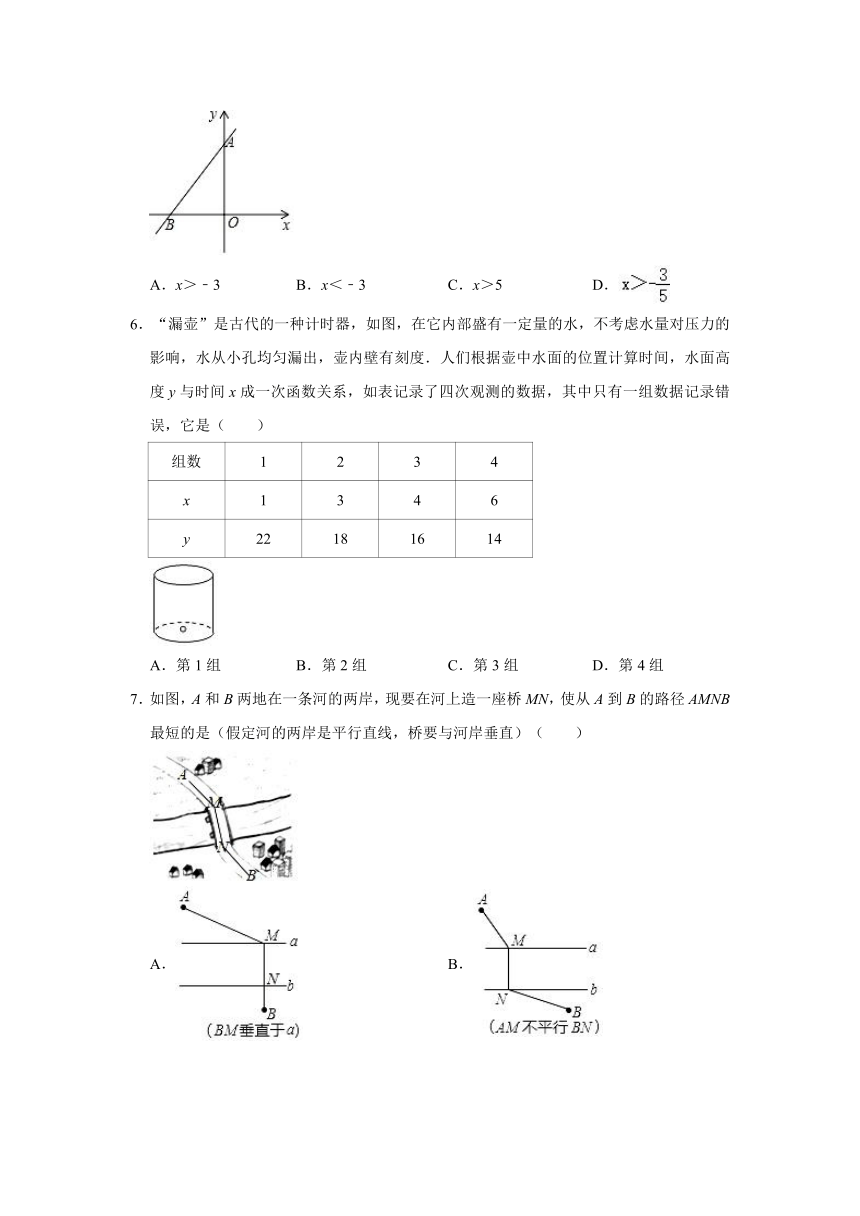
2020-2021学年山东省潍坊市青州市、临朐县、昌邑县、诸城市、昌乐县、寿光市八年级(下)期末数学试卷
一、选择题(共8个题,每小题3分,共24分).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
2.下列选项中,计算正确的是( )
A.3+2=5
B.﹣=
C.×=
D.÷=
3.如图所示,以A为圆心的圆交数轴于B,C两点,若A,B两点表示的数分别为1,,则点C表示的数是( )
A.﹣1
B.2﹣
C.2﹣2
D.1﹣
4.如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标是( )
A.(0,2)
B.(0,2.5)
C.(0,3)
D.(0,4)
5.如图,直线y=ax+b(a≠0)过点A(0,5),B(﹣3,0),则不等式ax+b>0的解集是( )
A.x>﹣3
B.x<﹣3
C.x>5
D.
6.“漏壶”是古代的一种计时器,如图,在它内部盛有一定量的水,不考虑水量对压力的影响,水从小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,水面高度y与时间x成一次函数关系,如表记录了四次观测的数据,其中只有一组数据记录错误,它是( )
组数
1
2
3
4
x
1
3
4
6
y
22
18
16
14
A.第1组
B.第2组
C.第3组
D.第4组
7.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.
B.
C.
D.
8.如图,△ABC的顶点A在y轴上,B,C两点都在x轴上,将边AB向右平移,平移后点A的对应点为D,点B的对应点为O,线段DO交AC于点E(2,),若AB=5,则点D的坐标为( )
A.(3,3)
B.(4,4)
C.(3,)
D.(3,4)
二、选择题(本题共4小题,每小题3分,共12分.在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分.)
9.若a>b,则下列不等式一定成立的是
.
A.a+2>b+2
B.<
C.﹣2a<﹣2b
D.a2<b2
10.满足下列条件的三角形中,是直角三角形的是
.
A.三个内角度数之比是1:2:3
B.三个外角度数比为2:3:4
C.三边长之比为5:12:13
D.三边长的平方之比是1:3:4
11.已知点A(﹣2,3)经变换后到点B,下面的说法正确的是
.
A.点A与点B关于x轴对称,则点B的坐标为B(2,3)
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为B(3,2)
C.点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2)
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为B(2,6)
12.如图,△ABC的两条中线BE,CD交于点O,则下列结论正确的是
.
A.BC=2DE
B.=
C.△ADE∽△ABC
D.S△DOE:S△BOC=1:4
三、填空题(本大题共6小题,共18分,只要求填写最后结果,每小题填对得3分)
13.满足a﹣2≥的最小整数a=
.
14.已知m=+,n=﹣,则m2﹣n2的值为
.
15.中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式=来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式=所对应两直线交点坐标是
.
16.如图,△ABC沿AC平移得到△A'B'C',A'B'交BC于点D,若AC=6,D是BC的中点,则C'C=
.
17.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B=
度.
18.如图,在△ABC中,∠ACB=90°,AE平分∠BAC,AE与BC交于点D,CD:BD=3:5,AC=3,BE⊥AE,则BE的长度为
.
四、解答题(本大题共6小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤)
19.计算:
(1)
(2)(3)(3)﹣()2.
20.解不等式组:,并将解集在数轴上表示出来.
21.如图,在△ABC中,点D在边AB上,AD=9,BD=7.AC=12.△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)若AF=8,求AE的长度.
22.某品牌山地自行车经销商经营的A型车去年销售总额为50000元,今年每辆车的售价比去年降低500元,若卖出的数量相同,销售总额将比去年减少12500元.A、B两种型号车今年的进货和销售价格信息如表所示.
A型车
B型车
进货价
1100元/辆
1400元/辆
销售价
2000元/辆
(1)今年A型车每辆售价为多少元?
(2)该品牌经销商计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的3倍,请问应如何安排两种型号车的进货数量,才能使这批越野自行车售出后获利最多?最大利润是多少?
23.如图,在正方形ABCD中,以边AD为边长在其内部构造等边△ADE,将△ADE绕点D逆时针旋转α(0°<α<60°),得到△A′DE′,AE与A′E′交于点F,连接AA′,EE′.
求证:(1)AA′=EE′;
(2)A′F=EF.
24.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0),点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出结果:线段AB的长
,点C的坐标
;
(2)求直线CD的函数表达式;
(3)点P在直线CD上,使得S△PAC=2S△OAB,求点P的坐标.
参考答案
一、选择题(共8个题,每小题3分,共24分).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据中心对称图形以及轴对称图形的概念对各选项分析判断即可得解.
解:A.不是轴对称图形,也不是中心对称图形,故本选项不合题意;
B.不是轴对称图形,是中心对称图形,故本选项不合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.既是轴对称图形,也是中心对称图形,故本选项符合题意.
故选:D.
2.下列选项中,计算正确的是( )
A.3+2=5
B.﹣=
C.×=
D.÷=
【分析】根据二次根式的加减法和乘除法可以判断各个选项中的式子是否正确.
解:3+2不能合并,故选项A不符合题意;
不能合并,故选项B不符合题意;
×=,故选项C符合题意;
=,故选项D不符合题意;
故选:C.
3.如图所示,以A为圆心的圆交数轴于B,C两点,若A,B两点表示的数分别为1,,则点C表示的数是( )
A.﹣1
B.2﹣
C.2﹣2
D.1﹣
【分析】根据数轴两点间的距离求出⊙A的半径AB=,从而得到AC=,即可求解.
解:∵A,B两点表示的数分别为1,,
∴,
∵AB=AC,
∴,
∵点C在点A的左边,
∴点C表示的数为,
故选:B.
4.如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标是( )
A.(0,2)
B.(0,2.5)
C.(0,3)
D.(0,4)
【分析】连接CF,交y轴于点P,根据位似图形的概念得到CD∥GF,根据相似三角形的性质求出GP,进而求出OP,得到答案.
解:连接CF,交y轴于点P,则点P为位似中心,
由题意得,CD=4,GF=2,DG=3,OG=1,
∵矩形OEFG与矩形ABCD是位似图形,
∴CD∥GF,
∴△CDP∽△FGP,
∴=,即=,
解得,GP=1,
∴OP=2,
∴位似中心P的坐标为(0,2)
故选:A.
5.如图,直线y=ax+b(a≠0)过点A(0,5),B(﹣3,0),则不等式ax+b>0的解集是( )
A.x>﹣3
B.x<﹣3
C.x>5
D.
【分析】写出函数图象在x轴上方所对应的自变量的范围即可.
解:当x>﹣3时,y>0,
所以不等式ax+b>0的解集为x>﹣3.
故选:A.
6.“漏壶”是古代的一种计时器,如图,在它内部盛有一定量的水,不考虑水量对压力的影响,水从小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,水面高度y与时间x成一次函数关系,如表记录了四次观测的数据,其中只有一组数据记录错误,它是( )
组数
1
2
3
4
x
1
3
4
6
y
22
18
16
14
A.第1组
B.第2组
C.第3组
D.第4组
【分析】根据题意,可知y随t的增大而减小,符合一次函数图象,从而可以解答本题.
解:∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,t表示漏水时间,y表示壶底到水面的高度,
∴y随t的增大而减小,且第1、2、3组数据满足y与x之间的关系式y=﹣2x+24,第4组数据不满足y与x之间的关系式y=﹣2x+24.
故选:D.
7.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.
B.
C.
D.
【分析】过A作河的垂线AH,要使最短,MN⊥直线a,AI=MN,连接BI即可得出N,作出AM、MN、BN即可.
解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),
只要AM+BN最短就行,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.连接IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
8.如图,△ABC的顶点A在y轴上,B,C两点都在x轴上,将边AB向右平移,平移后点A的对应点为D,点B的对应点为O,线段DO交AC于点E(2,),若AB=5,则点D的坐标为( )
A.(3,3)
B.(4,4)
C.(3,)
D.(3,4)
【分析】作DF⊥BC垂足为F,EG⊥BC,垂足为G,根据相似三角形的判定与性质得===,根据平移性质和勾股定理得OF,DF的长,由此可得答案.
解:如图,分别作DF⊥BC垂足为F,EG⊥BC,垂足为G,
∴∠OFE=∠OFD=90°,
∵E(2,),
∴OG=2,GE=,
∵△EOG和△DOF有公共角∠DOF,
∴△EOG∽△DOF,
∴===,
根据平移的性质可知OD=AB=5,
设OF=3x,则DF=4x,
在Rt△ODF中:OD2=DF2+OF2,
即52=(4x)2+(3x)2,
∴x=1或x=﹣1(舍去),
∴OF=3x=3,DF=4x=4.
故D点的坐标为(3,4).
故选:D.
二、选择题(本题共4小题,每小题3分,共12分.在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分.)
9.若a>b,则下列不等式一定成立的是
AC .
A.a+2>b+2
B.<
C.﹣2a<﹣2b
D.a2<b2
【分析】根据不等式的性质进行分析判断.
解:A、在不等式a>b的两边同时加上2,不等号的方向不变,即a+2>b+2,原变形正确,故此选项符合题意;
B、在不等式a>b的两边同时除以4,不等号的方向不变,即>,原变形错误,故此选项不符合题意;
C、在不等式a>b的两边同时乘以﹣2,不等号的方向改变,即﹣2a<﹣2b成立,原变形正确,故此选项符合题意;
D、当a>b>0时,不等式a2>b2成立,原变形错误,故此选项不符合题意.
故答案为:AC.
10.满足下列条件的三角形中,是直角三角形的是
ACD .
A.三个内角度数之比是1:2:3
B.三个外角度数比为2:3:4
C.三边长之比为5:12:13
D.三边长的平方之比是1:3:4
【分析】根据三角形内角和定理判断A;根据三角形外角和定理判断B;根据勾股定理的逆定理判断C和D.
解:当三个内角度数之比是1:2:3时,最大的角的度数是:180°×=90°,故选项A符合题意;
当三个外角度数比为2:3:4时,最小的外角是:360°×=80°,最大的角的度数是:180°﹣80°=100°>90°,故选项B不符合题意;
当三边长之比为5:12:13时,52+122=132,故该三角形是直角三角形,故选项C符合题意;
当三边长的平方比为1:3:4时,因为12+()2=22,故该三角形是直角三角形,故选项D符合题意;
故答案为:ACD.
11.已知点A(﹣2,3)经变换后到点B,下面的说法正确的是
B,D .
A.点A与点B关于x轴对称,则点B的坐标为B(2,3)
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为B(3,2)
C.点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2)
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为B(2,6)
【分析】根据轴对称,中心对称,旋转变换的性质一一判断即可.
解:A.点A与点B关于x轴对称,则点B的坐标为B(2,3),错误,应该是(﹣2,﹣3).
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为B(3,2),正确
C.点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2),错误,应该是(2,﹣3).
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为B(2,6),正确,
故答案为:B,D.
12.如图,△ABC的两条中线BE,CD交于点O,则下列结论正确的是
ACD .
A.BC=2DE
B.=
C.△ADE∽△ABC
D.S△DOE:S△BOC=1:4
【分析】先判断DE为△ABC的中位线,根据三角形中位线的性质得到BC=2DE,DE∥BC,则可对A选项进行判断;利用三角形面积公式得到S△ADC=S△ABC,S△ABE=S△ABC,则可对B选项进行判断;由DE∥BC得到△ADE∽△ABC,则可对C选项进行判断;利用O点为△ABC的重心得到OB=2OE,再由DE∥BC得到△ODE∽△OCB,然后根据相似三角形的性质可对D选项进行判断.
解:∵△ABC的两条中线BE,CD交于点O,
∴DE为△ABC的中位线,
∴BC=2DE,DE∥BC,所以A选项的结论正确;
∵D点为AB的中点,
∴S△ADC=S△ABC,
∵E点为AC的中点,
∴S△ABE=S△ABC,
∴S△ABE=S△ADC,所以B选项的结论错误;
∵DE∥BC,
∴△ADE∽△ABC,所以C选项的结论正确;
∵△ABC的两条中线BE,CD交于点O,
∴O点为△ABC的重心,
∴OB=2OE,
∵DE∥BC,
∴△ODE∽△OCB,
∴S△DOE:S△BOC=()2=1:4,所以D选项的结论正确.
故答案为ACD.
三、填空题(本大题共6小题,共18分,只要求填写最后结果,每小题填对得3分)
13.满足a﹣2≥的最小整数a= 9 .
【分析】求出不等式的解集,确定出最小整数a的值即可.
解:不等式a﹣2≥,
解得:a≥+2≈8.3,
则a﹣2≥的最小整数a=9.
故答案为:9.
14.已知m=+,n=﹣,则m2﹣n2的值为
4 .
【分析】先计算出m+n与m﹣n,再利用平方差公式得到m2﹣n2=(m+n)(m﹣n),然后利用整体代入的方法计算.
解:∵m=+,n=﹣,
∴m+n=2,m﹣n=2,
∴m2﹣n2=(m+n)(m﹣n)=2×2=4.
故答案为4.
15.中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式=来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式=所对应两直线交点坐标是 (2,5) .
【分析】根据题意得出方程组,求出方程组的解,再得出答案即可.
解:根据题意得:
,
①+②,得x=2,
把x=2代入①,得8﹣y=3,
解得:y=5,
所以方程组的解为,
∴两直线交点坐标是(2,5),
故答案为:(2,5).
16.如图,△ABC沿AC平移得到△A'B'C',A'B'交BC于点D,若AC=6,D是BC的中点,则C'C= 3 .
【分析】证明AA′=CA′=3,可得结论.
解:由平移的性质,可知,A′D∥AB,
∵BD=CD,
∴AA′=A′C=3,
∴CC′=AA′=3,
故答案为:3.
17.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B= 30 度.
【分析】证明∠CAB=2∠B,根据直角三角形两锐角互余,构建方程求解即可.
解:由作图可知,AD平分∠CAB,
∴∠CAD=∠DAB,
∵△DAC∽△ABC,
∴∠CAD=∠B,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为30.
18.如图,在△ABC中,∠ACB=90°,AE平分∠BAC,AE与BC交于点D,CD:BD=3:5,AC=3,BE⊥AE,则BE的长度为 .
【分析】设CD=3x,BD=5x,过D作DH⊥AB于H,根据HL定理证得Rt△ACD≌Rt△AHD,得到AH=AC=3,由勾股定理得到BH=4x,再根据勾股定理求出x,进而求出AD,根据三角形的面积公式即可求得BE.
解:设CD=3x,BD=5x,
过D作DH⊥AB于H,
∵∠ACB=90°,AE平分∠BAC,
∴DH=CD=3x,
在Rt△ACD和Rt△AHD中,
∴Rt△ACD≌Rt△AHD(HL),
∴AH=AC=3,
在Rt△BDH中,BH==4x,
在Rt△ABC中,
∵AB2=BC2+AC2,
∴(3+4x)2=(5x+3x)2+32,
解得:x1=0(不合题意,舍去),x2=,
∴BH=2,BH=CD=,
∴AB=5,
∴AD===,
∵S△ABD=AB?DH=AD?BE,
∴BE===,
故答案为:.
四、解答题(本大题共6小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤)
19.计算:
(1)
(2)(3)(3)﹣()2.
【分析】(1)利用二次根式的乘法法则运算;
(2)利用平方差公式和完全平方公式计算.
解:(1)原式=4+﹣+2
=3﹣+2
=3+;
(2)原式=18﹣12﹣(3﹣2+2)
=6﹣5+2
=1+2.
20.解不等式组:,并将解集在数轴上表示出来.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:解不等式3(x+2)>x﹣2,得x>﹣4;
解不等式,得x≤3,
将不等式组的解集表示在数轴上如下:
∴不等式组的解集为﹣4<x≤3.
21.如图,在△ABC中,点D在边AB上,AD=9,BD=7.AC=12.△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)若AF=8,求AE的长度.
【分析】(1)求得AB的长,利用AB:AC=AC:AD,且夹角相等,可证△ACD∽△ABC;
(2)利用△ACD∽△ABC,求得△ABE∽△ACF,再根据对应线段成比例求解.
解:(1)∵AD=9,BD=7,AC=12,
∴AB=AD+BD=16,
∵==,==,
∴=,
∵∠BAC=∠CAD,
∴△ACD∽△ABC;
(2)由(1)可知,△ACD∽△ABC,
∴∠ABF=∠ACF,
∵AE平分∠BAC,
∴∠BAE=∠CAF,
∴△ABE∽△ACF,
∴=,即=,
∴AE==.
22.某品牌山地自行车经销商经营的A型车去年销售总额为50000元,今年每辆车的售价比去年降低500元,若卖出的数量相同,销售总额将比去年减少12500元.A、B两种型号车今年的进货和销售价格信息如表所示.
A型车
B型车
进货价
1100元/辆
1400元/辆
销售价
2000元/辆
(1)今年A型车每辆售价为多少元?
(2)该品牌经销商计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的3倍,请问应如何安排两种型号车的进货数量,才能使这批越野自行车售出后获利最多?最大利润是多少?
【分析】(1)根据“A型车去年销售总额为50000元,今年每辆车的售价比去年降低500元,若卖出的数量相同,销售总额将比去年减少12500元”列出分式方程,解之即可;
(2)设经销商新进A型车a辆,则B型车为(60﹣a)辆,获利y元,则y=﹣200a+36000,根据“B型车的进货数量不超过A型车数量的3倍”列出不等式,求出a的取值范围,利用一次函数的性质即可得到最大利润.
解:(1)设今年A型车每辆售价为x元,根据题意得:
=,
解得x=1500,
经检验,x=1500是方程的解,且符合题意,
答:今年A型车每辆售价为1500元;
(2)设经销商新进A型车a辆,则B型车为(60﹣a)辆,获利y元,根据题意得:
y=(1500﹣1100)a+(2000﹣1400)(60﹣a)=﹣200a+36000,
∵B型车的进货数量不超过A型车数量的3倍,
∴60﹣a≤3a,
解得a≥15,
∵﹣200<0,
∴y随a的增大而减小,
∴a=15时,y的值最大,最大利润为33000元,
∴60﹣a=60﹣15=45,
∴当经销商新进A型车15辆,B型车45辆时,获利最多,最大利润为33000元.
23.如图,在正方形ABCD中,以边AD为边长在其内部构造等边△ADE,将△ADE绕点D逆时针旋转α(0°<α<60°),得到△A′DE′,AE与A′E′交于点F,连接AA′,EE′.
求证:(1)AA′=EE′;
(2)A′F=EF.
【分析】(1)利用旋转的性质得到∠ADA′=∠EDE′=α,DA=DA′,DE=DE′,再利用等边三角形的性质得到DA=DE,所以DA=DA′=DE=DE′,然后根据“SAS”证明△DAA′≌△DEE′,从而得到结论;
(2)先由△DAA′≌△DEE′得到∠DA′A=∠DE′E,则∠DA′A=∠DEE′,再证明∠AA′F=∠E′EF,然后根据“ASA”证明△AA′F≌△E′EF,从而得到结论.
【解答】证明:(1)∵△ADE绕点D逆时针旋转α得到△A′DE′
∴∠ADA′=∠EDE′=α,DA=DA′,DE=DE′,
∵△ADE为等边三角形,
∴DA=DE,
∴DA=DA′=DE=DE′,
在△DAA′和△DEE′中,
,
∴△DAA′≌△DEE′(SAS),
∴AA′=EE′;
(2)∵△DAA′≌△DEE′,
∴∠DA′A=∠DE′E,
而DE=DE′,
∴∠DA′A=∠DEE′,
∵△DAE和△DA′E′都为等边三角形,
∴∠DA′E′=∠DEA=60°,
∴∠AA′F=∠E′EF,
在△AA′F和△E′EF中,
,
∴△AA′F≌△E′EF(ASA),
∴A′F=EF.
24.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0),点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出结果:线段AB的长
5 ,点C的坐标
(8,0) ;
(2)求直线CD的函数表达式;
(3)点P在直线CD上,使得S△PAC=2S△OAB,求点P的坐标.
【分析】(1)利用勾股定理计算AB的长,再利用折叠的性质得到AC=AB=5,从而可确定C点坐标;
(2)设D(0,t),则BD=4﹣t,根据折叠的性质得到DC=DB=4﹣t,再在Rt△OCD中利用勾股定理得到t2+82=(4﹣t)2,则解方程得到D点坐标,然后利用待定系数法求直线CD的解析式;
(3)设P(m,m﹣6),先利用三角形面积公式计算出S△OAB=6,则S△PAC=12,利用三角形面积公式得到×5×|m﹣6|=12,然后解方程求出m,从而得到P点坐标.
解:(1)∵点A(3,0),点B(0,4),
∴AB==5,
∵将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,
∴AC=AB=5,
∴OC=OA+AC=8,
∴C(8,,0);
故答案为5,(8,0);
(2)设D(0,t),则BD=4﹣t,
∵将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,
∴DC=DB=4﹣t,
在Rt△OCD中,t2+82=(4﹣t)2,解得t=﹣6,
∴D(0,﹣6);
设直线CD的解析式为y=kx+b,
把C(8,0),D(0,﹣6)分别代入得,解得,
∴直线CD的解析式为y=x﹣6;
(3)设P(m,m﹣6),
∵S△OAB=×3×4=6,
而S△PAC=2S△OAB,
∴S△PAC=12,
即×5×|m﹣6|=12,解得m=或,
∴P点坐标为(,﹣)或(,).
一、选择题(共8个题,每小题3分,共24分).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
2.下列选项中,计算正确的是( )
A.3+2=5
B.﹣=
C.×=
D.÷=
3.如图所示,以A为圆心的圆交数轴于B,C两点,若A,B两点表示的数分别为1,,则点C表示的数是( )
A.﹣1
B.2﹣
C.2﹣2
D.1﹣
4.如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标是( )
A.(0,2)
B.(0,2.5)
C.(0,3)
D.(0,4)
5.如图,直线y=ax+b(a≠0)过点A(0,5),B(﹣3,0),则不等式ax+b>0的解集是( )
A.x>﹣3
B.x<﹣3
C.x>5
D.
6.“漏壶”是古代的一种计时器,如图,在它内部盛有一定量的水,不考虑水量对压力的影响,水从小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,水面高度y与时间x成一次函数关系,如表记录了四次观测的数据,其中只有一组数据记录错误,它是( )
组数
1
2
3
4
x
1
3
4
6
y
22
18
16
14
A.第1组
B.第2组
C.第3组
D.第4组
7.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.
B.
C.
D.
8.如图,△ABC的顶点A在y轴上,B,C两点都在x轴上,将边AB向右平移,平移后点A的对应点为D,点B的对应点为O,线段DO交AC于点E(2,),若AB=5,则点D的坐标为( )
A.(3,3)
B.(4,4)
C.(3,)
D.(3,4)
二、选择题(本题共4小题,每小题3分,共12分.在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分.)
9.若a>b,则下列不等式一定成立的是
.
A.a+2>b+2
B.<
C.﹣2a<﹣2b
D.a2<b2
10.满足下列条件的三角形中,是直角三角形的是
.
A.三个内角度数之比是1:2:3
B.三个外角度数比为2:3:4
C.三边长之比为5:12:13
D.三边长的平方之比是1:3:4
11.已知点A(﹣2,3)经变换后到点B,下面的说法正确的是
.
A.点A与点B关于x轴对称,则点B的坐标为B(2,3)
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为B(3,2)
C.点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2)
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为B(2,6)
12.如图,△ABC的两条中线BE,CD交于点O,则下列结论正确的是
.
A.BC=2DE
B.=
C.△ADE∽△ABC
D.S△DOE:S△BOC=1:4
三、填空题(本大题共6小题,共18分,只要求填写最后结果,每小题填对得3分)
13.满足a﹣2≥的最小整数a=
.
14.已知m=+,n=﹣,则m2﹣n2的值为
.
15.中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式=来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式=所对应两直线交点坐标是
.
16.如图,△ABC沿AC平移得到△A'B'C',A'B'交BC于点D,若AC=6,D是BC的中点,则C'C=
.
17.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B=
度.
18.如图,在△ABC中,∠ACB=90°,AE平分∠BAC,AE与BC交于点D,CD:BD=3:5,AC=3,BE⊥AE,则BE的长度为
.
四、解答题(本大题共6小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤)
19.计算:
(1)
(2)(3)(3)﹣()2.
20.解不等式组:,并将解集在数轴上表示出来.
21.如图,在△ABC中,点D在边AB上,AD=9,BD=7.AC=12.△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)若AF=8,求AE的长度.
22.某品牌山地自行车经销商经营的A型车去年销售总额为50000元,今年每辆车的售价比去年降低500元,若卖出的数量相同,销售总额将比去年减少12500元.A、B两种型号车今年的进货和销售价格信息如表所示.
A型车
B型车
进货价
1100元/辆
1400元/辆
销售价
2000元/辆
(1)今年A型车每辆售价为多少元?
(2)该品牌经销商计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的3倍,请问应如何安排两种型号车的进货数量,才能使这批越野自行车售出后获利最多?最大利润是多少?
23.如图,在正方形ABCD中,以边AD为边长在其内部构造等边△ADE,将△ADE绕点D逆时针旋转α(0°<α<60°),得到△A′DE′,AE与A′E′交于点F,连接AA′,EE′.
求证:(1)AA′=EE′;
(2)A′F=EF.
24.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0),点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出结果:线段AB的长
,点C的坐标
;
(2)求直线CD的函数表达式;
(3)点P在直线CD上,使得S△PAC=2S△OAB,求点P的坐标.
参考答案
一、选择题(共8个题,每小题3分,共24分).
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据中心对称图形以及轴对称图形的概念对各选项分析判断即可得解.
解:A.不是轴对称图形,也不是中心对称图形,故本选项不合题意;
B.不是轴对称图形,是中心对称图形,故本选项不合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.既是轴对称图形,也是中心对称图形,故本选项符合题意.
故选:D.
2.下列选项中,计算正确的是( )
A.3+2=5
B.﹣=
C.×=
D.÷=
【分析】根据二次根式的加减法和乘除法可以判断各个选项中的式子是否正确.
解:3+2不能合并,故选项A不符合题意;
不能合并,故选项B不符合题意;
×=,故选项C符合题意;
=,故选项D不符合题意;
故选:C.
3.如图所示,以A为圆心的圆交数轴于B,C两点,若A,B两点表示的数分别为1,,则点C表示的数是( )
A.﹣1
B.2﹣
C.2﹣2
D.1﹣
【分析】根据数轴两点间的距离求出⊙A的半径AB=,从而得到AC=,即可求解.
解:∵A,B两点表示的数分别为1,,
∴,
∵AB=AC,
∴,
∵点C在点A的左边,
∴点C表示的数为,
故选:B.
4.如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标是( )
A.(0,2)
B.(0,2.5)
C.(0,3)
D.(0,4)
【分析】连接CF,交y轴于点P,根据位似图形的概念得到CD∥GF,根据相似三角形的性质求出GP,进而求出OP,得到答案.
解:连接CF,交y轴于点P,则点P为位似中心,
由题意得,CD=4,GF=2,DG=3,OG=1,
∵矩形OEFG与矩形ABCD是位似图形,
∴CD∥GF,
∴△CDP∽△FGP,
∴=,即=,
解得,GP=1,
∴OP=2,
∴位似中心P的坐标为(0,2)
故选:A.
5.如图,直线y=ax+b(a≠0)过点A(0,5),B(﹣3,0),则不等式ax+b>0的解集是( )
A.x>﹣3
B.x<﹣3
C.x>5
D.
【分析】写出函数图象在x轴上方所对应的自变量的范围即可.
解:当x>﹣3时,y>0,
所以不等式ax+b>0的解集为x>﹣3.
故选:A.
6.“漏壶”是古代的一种计时器,如图,在它内部盛有一定量的水,不考虑水量对压力的影响,水从小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,水面高度y与时间x成一次函数关系,如表记录了四次观测的数据,其中只有一组数据记录错误,它是( )
组数
1
2
3
4
x
1
3
4
6
y
22
18
16
14
A.第1组
B.第2组
C.第3组
D.第4组
【分析】根据题意,可知y随t的增大而减小,符合一次函数图象,从而可以解答本题.
解:∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,t表示漏水时间,y表示壶底到水面的高度,
∴y随t的增大而减小,且第1、2、3组数据满足y与x之间的关系式y=﹣2x+24,第4组数据不满足y与x之间的关系式y=﹣2x+24.
故选:D.
7.如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( )
A.
B.
C.
D.
【分析】过A作河的垂线AH,要使最短,MN⊥直线a,AI=MN,连接BI即可得出N,作出AM、MN、BN即可.
解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),
只要AM+BN最短就行,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.连接IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
8.如图,△ABC的顶点A在y轴上,B,C两点都在x轴上,将边AB向右平移,平移后点A的对应点为D,点B的对应点为O,线段DO交AC于点E(2,),若AB=5,则点D的坐标为( )
A.(3,3)
B.(4,4)
C.(3,)
D.(3,4)
【分析】作DF⊥BC垂足为F,EG⊥BC,垂足为G,根据相似三角形的判定与性质得===,根据平移性质和勾股定理得OF,DF的长,由此可得答案.
解:如图,分别作DF⊥BC垂足为F,EG⊥BC,垂足为G,
∴∠OFE=∠OFD=90°,
∵E(2,),
∴OG=2,GE=,
∵△EOG和△DOF有公共角∠DOF,
∴△EOG∽△DOF,
∴===,
根据平移的性质可知OD=AB=5,
设OF=3x,则DF=4x,
在Rt△ODF中:OD2=DF2+OF2,
即52=(4x)2+(3x)2,
∴x=1或x=﹣1(舍去),
∴OF=3x=3,DF=4x=4.
故D点的坐标为(3,4).
故选:D.
二、选择题(本题共4小题,每小题3分,共12分.在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分.)
9.若a>b,则下列不等式一定成立的是
AC .
A.a+2>b+2
B.<
C.﹣2a<﹣2b
D.a2<b2
【分析】根据不等式的性质进行分析判断.
解:A、在不等式a>b的两边同时加上2,不等号的方向不变,即a+2>b+2,原变形正确,故此选项符合题意;
B、在不等式a>b的两边同时除以4,不等号的方向不变,即>,原变形错误,故此选项不符合题意;
C、在不等式a>b的两边同时乘以﹣2,不等号的方向改变,即﹣2a<﹣2b成立,原变形正确,故此选项符合题意;
D、当a>b>0时,不等式a2>b2成立,原变形错误,故此选项不符合题意.
故答案为:AC.
10.满足下列条件的三角形中,是直角三角形的是
ACD .
A.三个内角度数之比是1:2:3
B.三个外角度数比为2:3:4
C.三边长之比为5:12:13
D.三边长的平方之比是1:3:4
【分析】根据三角形内角和定理判断A;根据三角形外角和定理判断B;根据勾股定理的逆定理判断C和D.
解:当三个内角度数之比是1:2:3时,最大的角的度数是:180°×=90°,故选项A符合题意;
当三个外角度数比为2:3:4时,最小的外角是:360°×=80°,最大的角的度数是:180°﹣80°=100°>90°,故选项B不符合题意;
当三边长之比为5:12:13时,52+122=132,故该三角形是直角三角形,故选项C符合题意;
当三边长的平方比为1:3:4时,因为12+()2=22,故该三角形是直角三角形,故选项D符合题意;
故答案为:ACD.
11.已知点A(﹣2,3)经变换后到点B,下面的说法正确的是
B,D .
A.点A与点B关于x轴对称,则点B的坐标为B(2,3)
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为B(3,2)
C.点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2)
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为B(2,6)
【分析】根据轴对称,中心对称,旋转变换的性质一一判断即可.
解:A.点A与点B关于x轴对称,则点B的坐标为B(2,3),错误,应该是(﹣2,﹣3).
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为B(3,2),正确
C.点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2),错误,应该是(2,﹣3).
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为B(2,6),正确,
故答案为:B,D.
12.如图,△ABC的两条中线BE,CD交于点O,则下列结论正确的是
ACD .
A.BC=2DE
B.=
C.△ADE∽△ABC
D.S△DOE:S△BOC=1:4
【分析】先判断DE为△ABC的中位线,根据三角形中位线的性质得到BC=2DE,DE∥BC,则可对A选项进行判断;利用三角形面积公式得到S△ADC=S△ABC,S△ABE=S△ABC,则可对B选项进行判断;由DE∥BC得到△ADE∽△ABC,则可对C选项进行判断;利用O点为△ABC的重心得到OB=2OE,再由DE∥BC得到△ODE∽△OCB,然后根据相似三角形的性质可对D选项进行判断.
解:∵△ABC的两条中线BE,CD交于点O,
∴DE为△ABC的中位线,
∴BC=2DE,DE∥BC,所以A选项的结论正确;
∵D点为AB的中点,
∴S△ADC=S△ABC,
∵E点为AC的中点,
∴S△ABE=S△ABC,
∴S△ABE=S△ADC,所以B选项的结论错误;
∵DE∥BC,
∴△ADE∽△ABC,所以C选项的结论正确;
∵△ABC的两条中线BE,CD交于点O,
∴O点为△ABC的重心,
∴OB=2OE,
∵DE∥BC,
∴△ODE∽△OCB,
∴S△DOE:S△BOC=()2=1:4,所以D选项的结论正确.
故答案为ACD.
三、填空题(本大题共6小题,共18分,只要求填写最后结果,每小题填对得3分)
13.满足a﹣2≥的最小整数a= 9 .
【分析】求出不等式的解集,确定出最小整数a的值即可.
解:不等式a﹣2≥,
解得:a≥+2≈8.3,
则a﹣2≥的最小整数a=9.
故答案为:9.
14.已知m=+,n=﹣,则m2﹣n2的值为
4 .
【分析】先计算出m+n与m﹣n,再利用平方差公式得到m2﹣n2=(m+n)(m﹣n),然后利用整体代入的方法计算.
解:∵m=+,n=﹣,
∴m+n=2,m﹣n=2,
∴m2﹣n2=(m+n)(m﹣n)=2×2=4.
故答案为4.
15.中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式=来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式=所对应两直线交点坐标是 (2,5) .
【分析】根据题意得出方程组,求出方程组的解,再得出答案即可.
解:根据题意得:
,
①+②,得x=2,
把x=2代入①,得8﹣y=3,
解得:y=5,
所以方程组的解为,
∴两直线交点坐标是(2,5),
故答案为:(2,5).
16.如图,△ABC沿AC平移得到△A'B'C',A'B'交BC于点D,若AC=6,D是BC的中点,则C'C= 3 .
【分析】证明AA′=CA′=3,可得结论.
解:由平移的性质,可知,A′D∥AB,
∵BD=CD,
∴AA′=A′C=3,
∴CC′=AA′=3,
故答案为:3.
17.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B= 30 度.
【分析】证明∠CAB=2∠B,根据直角三角形两锐角互余,构建方程求解即可.
解:由作图可知,AD平分∠CAB,
∴∠CAD=∠DAB,
∵△DAC∽△ABC,
∴∠CAD=∠B,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为30.
18.如图,在△ABC中,∠ACB=90°,AE平分∠BAC,AE与BC交于点D,CD:BD=3:5,AC=3,BE⊥AE,则BE的长度为 .
【分析】设CD=3x,BD=5x,过D作DH⊥AB于H,根据HL定理证得Rt△ACD≌Rt△AHD,得到AH=AC=3,由勾股定理得到BH=4x,再根据勾股定理求出x,进而求出AD,根据三角形的面积公式即可求得BE.
解:设CD=3x,BD=5x,
过D作DH⊥AB于H,
∵∠ACB=90°,AE平分∠BAC,
∴DH=CD=3x,
在Rt△ACD和Rt△AHD中,
∴Rt△ACD≌Rt△AHD(HL),
∴AH=AC=3,
在Rt△BDH中,BH==4x,
在Rt△ABC中,
∵AB2=BC2+AC2,
∴(3+4x)2=(5x+3x)2+32,
解得:x1=0(不合题意,舍去),x2=,
∴BH=2,BH=CD=,
∴AB=5,
∴AD===,
∵S△ABD=AB?DH=AD?BE,
∴BE===,
故答案为:.
四、解答题(本大题共6小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤)
19.计算:
(1)
(2)(3)(3)﹣()2.
【分析】(1)利用二次根式的乘法法则运算;
(2)利用平方差公式和完全平方公式计算.
解:(1)原式=4+﹣+2
=3﹣+2
=3+;
(2)原式=18﹣12﹣(3﹣2+2)
=6﹣5+2
=1+2.
20.解不等式组:,并将解集在数轴上表示出来.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:解不等式3(x+2)>x﹣2,得x>﹣4;
解不等式,得x≤3,
将不等式组的解集表示在数轴上如下:
∴不等式组的解集为﹣4<x≤3.
21.如图,在△ABC中,点D在边AB上,AD=9,BD=7.AC=12.△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)若AF=8,求AE的长度.
【分析】(1)求得AB的长,利用AB:AC=AC:AD,且夹角相等,可证△ACD∽△ABC;
(2)利用△ACD∽△ABC,求得△ABE∽△ACF,再根据对应线段成比例求解.
解:(1)∵AD=9,BD=7,AC=12,
∴AB=AD+BD=16,
∵==,==,
∴=,
∵∠BAC=∠CAD,
∴△ACD∽△ABC;
(2)由(1)可知,△ACD∽△ABC,
∴∠ABF=∠ACF,
∵AE平分∠BAC,
∴∠BAE=∠CAF,
∴△ABE∽△ACF,
∴=,即=,
∴AE==.
22.某品牌山地自行车经销商经营的A型车去年销售总额为50000元,今年每辆车的售价比去年降低500元,若卖出的数量相同,销售总额将比去年减少12500元.A、B两种型号车今年的进货和销售价格信息如表所示.
A型车
B型车
进货价
1100元/辆
1400元/辆
销售价
2000元/辆
(1)今年A型车每辆售价为多少元?
(2)该品牌经销商计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的3倍,请问应如何安排两种型号车的进货数量,才能使这批越野自行车售出后获利最多?最大利润是多少?
【分析】(1)根据“A型车去年销售总额为50000元,今年每辆车的售价比去年降低500元,若卖出的数量相同,销售总额将比去年减少12500元”列出分式方程,解之即可;
(2)设经销商新进A型车a辆,则B型车为(60﹣a)辆,获利y元,则y=﹣200a+36000,根据“B型车的进货数量不超过A型车数量的3倍”列出不等式,求出a的取值范围,利用一次函数的性质即可得到最大利润.
解:(1)设今年A型车每辆售价为x元,根据题意得:
=,
解得x=1500,
经检验,x=1500是方程的解,且符合题意,
答:今年A型车每辆售价为1500元;
(2)设经销商新进A型车a辆,则B型车为(60﹣a)辆,获利y元,根据题意得:
y=(1500﹣1100)a+(2000﹣1400)(60﹣a)=﹣200a+36000,
∵B型车的进货数量不超过A型车数量的3倍,
∴60﹣a≤3a,
解得a≥15,
∵﹣200<0,
∴y随a的增大而减小,
∴a=15时,y的值最大,最大利润为33000元,
∴60﹣a=60﹣15=45,
∴当经销商新进A型车15辆,B型车45辆时,获利最多,最大利润为33000元.
23.如图,在正方形ABCD中,以边AD为边长在其内部构造等边△ADE,将△ADE绕点D逆时针旋转α(0°<α<60°),得到△A′DE′,AE与A′E′交于点F,连接AA′,EE′.
求证:(1)AA′=EE′;
(2)A′F=EF.
【分析】(1)利用旋转的性质得到∠ADA′=∠EDE′=α,DA=DA′,DE=DE′,再利用等边三角形的性质得到DA=DE,所以DA=DA′=DE=DE′,然后根据“SAS”证明△DAA′≌△DEE′,从而得到结论;
(2)先由△DAA′≌△DEE′得到∠DA′A=∠DE′E,则∠DA′A=∠DEE′,再证明∠AA′F=∠E′EF,然后根据“ASA”证明△AA′F≌△E′EF,从而得到结论.
【解答】证明:(1)∵△ADE绕点D逆时针旋转α得到△A′DE′
∴∠ADA′=∠EDE′=α,DA=DA′,DE=DE′,
∵△ADE为等边三角形,
∴DA=DE,
∴DA=DA′=DE=DE′,
在△DAA′和△DEE′中,
,
∴△DAA′≌△DEE′(SAS),
∴AA′=EE′;
(2)∵△DAA′≌△DEE′,
∴∠DA′A=∠DE′E,
而DE=DE′,
∴∠DA′A=∠DEE′,
∵△DAE和△DA′E′都为等边三角形,
∴∠DA′E′=∠DEA=60°,
∴∠AA′F=∠E′EF,
在△AA′F和△E′EF中,
,
∴△AA′F≌△E′EF(ASA),
∴A′F=EF.
24.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0),点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出结果:线段AB的长
5 ,点C的坐标
(8,0) ;
(2)求直线CD的函数表达式;
(3)点P在直线CD上,使得S△PAC=2S△OAB,求点P的坐标.
【分析】(1)利用勾股定理计算AB的长,再利用折叠的性质得到AC=AB=5,从而可确定C点坐标;
(2)设D(0,t),则BD=4﹣t,根据折叠的性质得到DC=DB=4﹣t,再在Rt△OCD中利用勾股定理得到t2+82=(4﹣t)2,则解方程得到D点坐标,然后利用待定系数法求直线CD的解析式;
(3)设P(m,m﹣6),先利用三角形面积公式计算出S△OAB=6,则S△PAC=12,利用三角形面积公式得到×5×|m﹣6|=12,然后解方程求出m,从而得到P点坐标.
解:(1)∵点A(3,0),点B(0,4),
∴AB==5,
∵将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,
∴AC=AB=5,
∴OC=OA+AC=8,
∴C(8,,0);
故答案为5,(8,0);
(2)设D(0,t),则BD=4﹣t,
∵将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,
∴DC=DB=4﹣t,
在Rt△OCD中,t2+82=(4﹣t)2,解得t=﹣6,
∴D(0,﹣6);
设直线CD的解析式为y=kx+b,
把C(8,0),D(0,﹣6)分别代入得,解得,
∴直线CD的解析式为y=x﹣6;
(3)设P(m,m﹣6),
∵S△OAB=×3×4=6,
而S△PAC=2S△OAB,
∴S△PAC=12,
即×5×|m﹣6|=12,解得m=或,
∴P点坐标为(,﹣)或(,).
同课章节目录
