3.4等腰梯形的性质和判定

(共19张PPT)
兴化市板桥初级中学初二备课组
1.4 等腰梯形的性质和判定
学习目标：
1、会能证明等腰梯形的性质定理和判定定理。
2、逐步学会分析和综合的思考方法，发展思考能力。
3、经历证明的过程，不断感受证明的必要性、感受合情
推理和演绎推理都是人们正确认识事物的重要途径。
4、感受探索活动中所体现的转化的数学思想方法。
1．等腰梯形概念：
_______________________________的图形叫做等腰梯形
2．等腰梯形的判定：
______________________________
3．等腰梯形的性质：
_______________________________
_______________________________
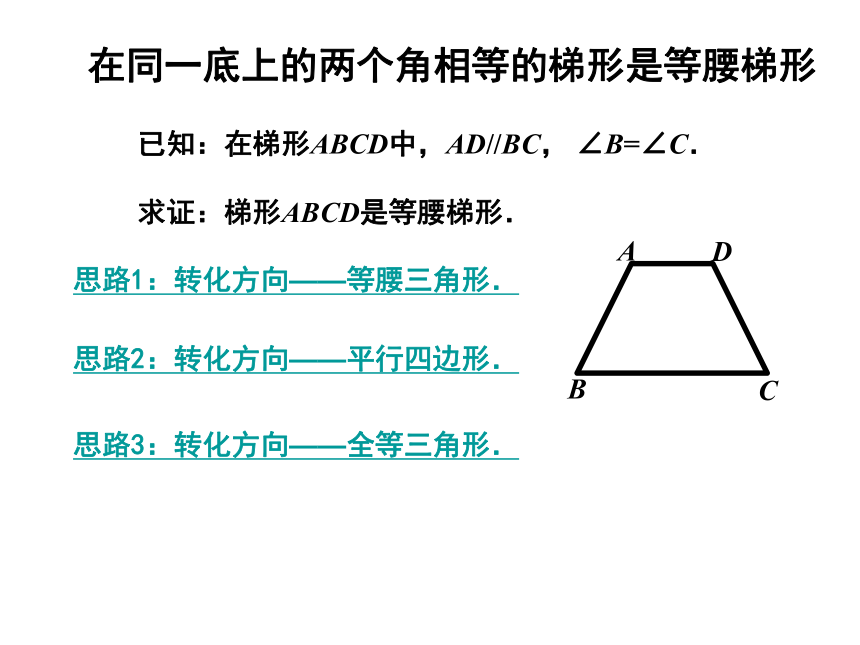
在同一底上的两个角相等的梯形是等腰梯形
已知：在梯形ABCD中，AD//BC， ∠B=∠C．
求证：梯形ABCD是等腰梯形．
A
B
C
D
思路1：转化方向——等腰三角形．
思路2：转化方向——平行四边形．
思路3：转化方向——全等三角形．
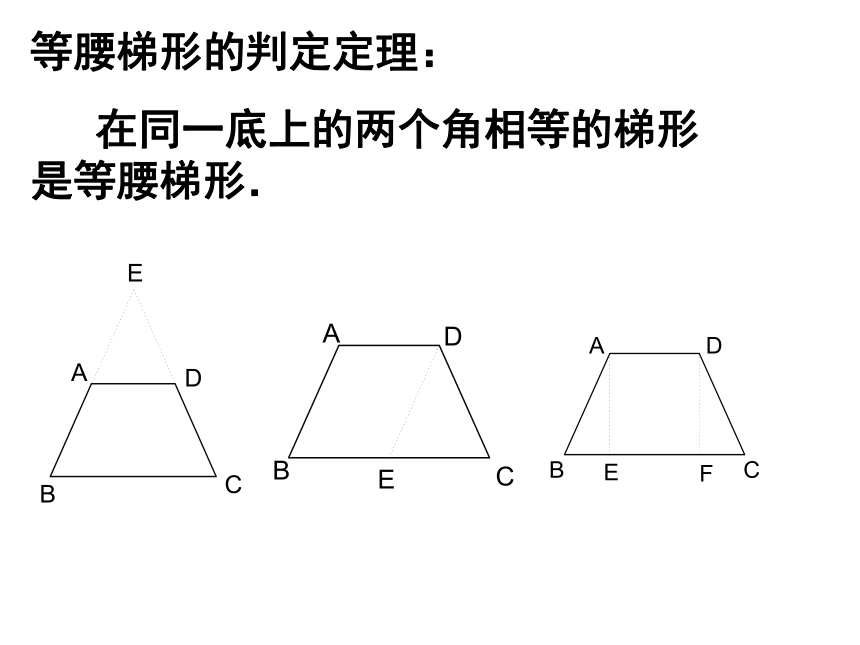
等腰梯形的判定定理：
在同一底上的两个角相等的梯形是等腰梯形．
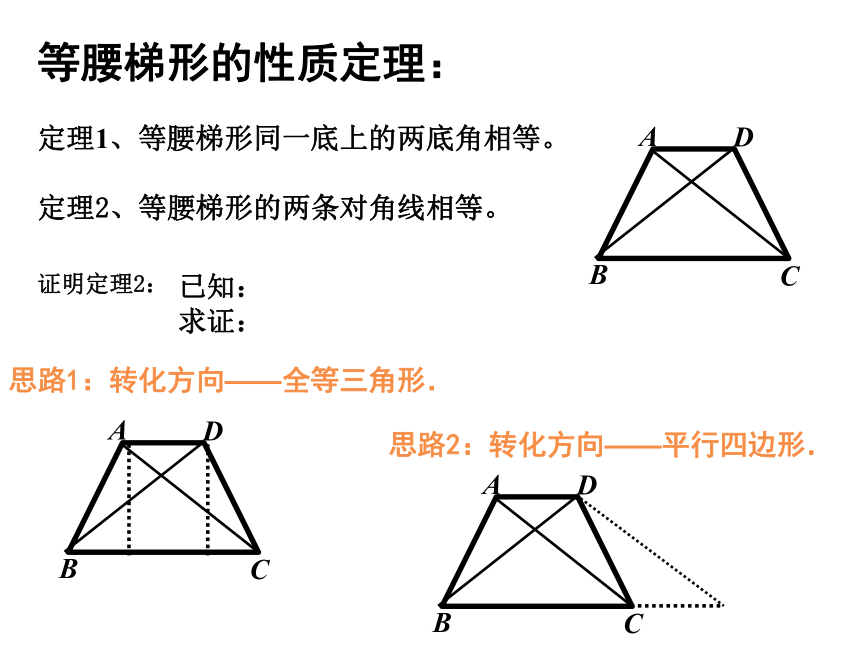
等腰梯形的性质定理：
定理1、等腰梯形同一底上的两底角相等。
定理2、等腰梯形的两条对角线相等。
证明定理2：
已知：
求证：
A
B
C
D
A
B
C
D
思路1：转化方向——全等三角形．
思路2：转化方向——平行四边形．
A
B
C
D
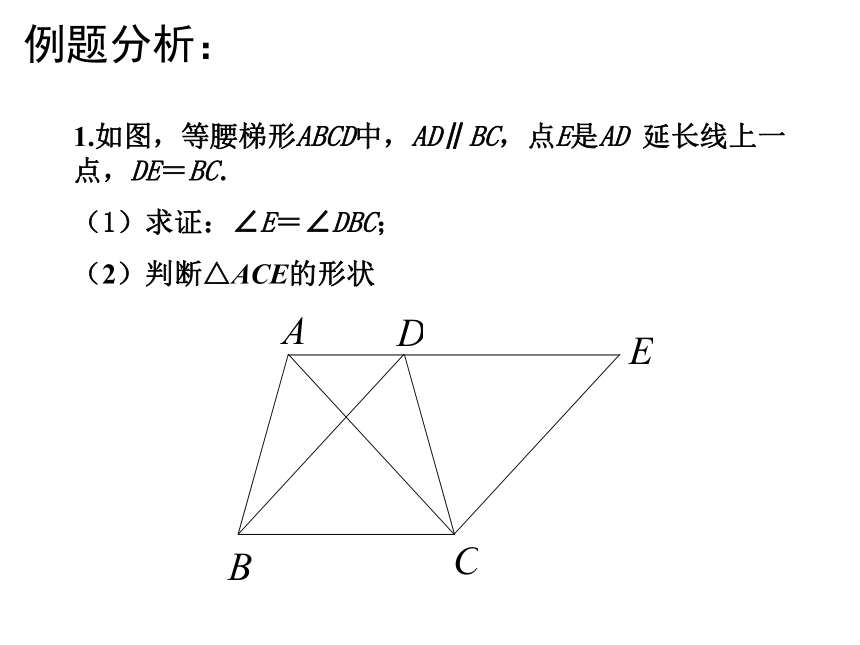
例题分析：
1.如图，等腰梯形ABCD中，AD∥BC，点E是AD 延长线上一点，DE＝BC．
（1）求证：∠E＝∠DBC；
（2）判断△ACE的形状
例题分析：
2.已知，在梯形ABCD中，AD∥BC，点E是BC 边的中点，EM⊥AB，EN⊥CD，垂足分别为M、N且 EM=EN．
求证：梯形ABCD是等腰梯形。
A
B
C
D
E
M
N
例题分析：
3.如图，已知在梯形ABCD中，AD∥BC，AB=DC，对角线AC和BD相交于点O，E是BC边上的一个动点（点E不于B、C两点重合），EF∥BD交AC于点F。EG∥AC交BD于点G。
（1）、求证：四边形EFOG的周长等于2OB；
（2）、请将上述题目的条件“梯形ABCD中，AD∥BC，AB=DC”改为另一种四边形，其他条件不变，使得结论“四边形EFOG的周长等于2OB”仍成立，并将改编后的题目画出图形，写出已知、求证，不必证明。
A
B
C
D
G
E
F
O
练习
1.如图，梯形ABCD中，AB∥CD，点E、F、G分别是BD、AC、DC的中点.已知两底差是6，两腰和是12，则△EFG的周长是（ ）
A.8 B.9 C.10 D.12
A
B
C
D
E
F
G
2.已知直角梯形ABCD中， AD∥BC，∠BCD=90°, BC = CD=2AD , E、F分别是BC、CD边的中点，连接BF、DE交于点P，连接CP并延长交AB于点Q，连接AF，则下列结论不正确的是（ ）
A . CP 平分∠BCD
B. 四边形 ABED 为平行四边形
C. CQ将直角梯形 ABCD 分为面积相等的两部分
D. △ABF为等腰三角形
3. 如图，已知梯形ABCD，AD∥BC，对角线AC，BD相交于点O，△AOD与△BOC的面积之比为1：9，若AD=1，则BC的长是 ．
4.如图，在梯形ABCD中，AB∥DC，∠ADC的平分线与∠BCD的平分线的交点E恰在AB上．若AD＝7cm，BC＝8cm，则AB的长度是 cm．
5.已知，在梯形ABCD中，AD∥BC，∠ABC=900，BC=2AD，E是BC的中点，连接AE、AC.
（1）点F是DC上一点，连接EF，交AC于点O（如图①），求证：△AOE∽△COF
（2）若点F是DC的中点，连接BD，交AE于点G（如图②），求证：四边形EFDG是菱形。
6.如图，梯形ABCD中，AD∥BC，∠DCB＝45°，CD ＝2，BD⊥CD ．过点C作CE⊥AB于E，交对角线BD于F．点G为BC中点，连结EG、AF．
(1)求EG的长；
(2)求证：CF ＝AB ＋AF．
小结与思考：
解决梯形问题常用的方法：
（1）平移腰：构造平行四边形
（2）“作高”：使两腰在两个直角三角形中．
（3）“平移对角线”：使两条对角线在同一个三角形中．
（4）“延长两腰”：构造具有公共角的两个等腰三角形．
（5）取一腰的中点：构造全等三角形，将上底下移
新问题
老问题
等腰梯形
三角形或特殊四边形
转化
转化
学有所获
思路1：转化方向——等腰三角形．
证明：延长BA，CD相交于点E.
∵∠B=∠C，
∴BE=CE.
∵四边形ABCD是梯形，
∴AD∥BC.
∴∠EAD=∠B,∠EDA=∠C.
∴∠EAD=∠EDA.
∴AE=DE.
∴AB=CD．
∴梯形ABCD是等腰梯形.
思路2：转化方向——平行四边形．
证明：过点A作AE∥DC，交BC于点E.
此时四边形AECD是平行四边形.
则AE∥CD且AE=CD，
∴∠AEB=∠C.
又∵∠B=∠C，
∴∠B=∠AEB.
∴AB=AE.
∴AB=CD.
∴梯形ABCD是等腰梯形.
思路3：转化方向——全等三角形．
证明：过点A作AE⊥BC，DF⊥BC，垂足分别为点E，F，
则有∠AEB=∠DFC.
∵AD∥BC，
∴AE=DF，
∵∠B=∠C，
∴△AEB≌△DFC(AAS)．
∴AB=CD.
∴梯形ABCD是等腰梯形.