山东青岛市2011—2012学年度第二学期八年级下数学期末模拟试卷及答案
文档属性
| 名称 | 山东青岛市2011—2012学年度第二学期八年级下数学期末模拟试卷及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-10 09:36:45 | ||
图片预览




文档简介
山东省青岛市2011—2012学年度第二学期八年级
下数学期末模拟试卷
A卷(共100分)
一、选择题:(本大题共有10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是正确的,把正确选项的代号填在题后的括号内.
1、排列做操队形时,甲、乙、丙位置如图所示,
甲对乙说,如果我的位置用(0,0)来表示,
你的位置用(2,1)表示,那么丙的位置是( )
(A)(5,4) (B)(4,5)
(C)(3,4) (D)(4、3)
2.4辆板车和5辆卡车一次能运27吨货,10辆
板车和3车卡车一次能运货20吨,设每辆板
车每次可运x吨货,每辆卡车每次能运y吨货,则可列方程组( )
(A) (B)
(C) (D)
3.能判定一个四边形是菱形的条件是( )
(A)对角线相等且互相垂直 (B)对角线相等且互相平分
(C)对角线互相垂直 (D)对角线互相垂直平分
4、在平面直角坐标系中,位于第二象限的点是( )
(A) (-2,-3) (B) (2,4) (C) (-2,3) (D) (2,3)
5、下列几组数据能作为直角三角形的三边长的是( )
(A) 2,3,4 (B) 5,3,4 (C) 4,6,9 (D) 5,11,13
6、已知是方程的一个解,那么 HYPERLINK "http://www./" 的值是( )
(A) 1 (B)3 (C)-3 (D) -1
7、下列图形中,既是轴对称又是中心对称的图形是( )
(A)正三角形 (B)平行四边形 (C)等腰梯形 (D)正方形
8、在平面直角坐标系中,直线不经过( )
(A)第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
9、如图,将一张矩形纸片对折后再对折,然后沿着图中的虚线剪下,得到①、②两部分,将②展开后得到的平面图形是( )
(A) 矩形 (B)平行四边形 (C)梯形 (D) 菱形
10、如图,再平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0)、(5,0)、(2,3),则顶点C的坐标是( ).
(A) (3,7) (B) (5,3) (C) (7,3) (D)(8,2)
二、填空题:(每小题4分,共16分)
11、若,那么 HYPERLINK "http://www./" =_________
12、若菱形的两条对角线长分别为6cm,8cm,则其周长为_________cm。
13、对于一次函数,如果 HYPERLINK "http://www./" ,那么(填“>”、“=”、“<”)。
14、如图是用形状、大小完全相同的等腰梯形密铺成的图案的一部分,则该图案中等腰梯形的较大内角的度数为_________度。
三、(第15题每小题6分,第16题6分,共18分)
15、解下列各题:
(1) 解方程组: HYPERLINK "http://www./"
(2)化简:
16、如果为的算术平方根,为 HYPERLINK "http://www./" 的立方根,求的平方根。
四、(每小题8分,共16分)
17、已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF。
求证:AF=DC;
若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论。
18、某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李票(元)与行李质量 HYPERLINK "http://www./" (千克)间的一次函数关系式为,现知贝贝带了60千克的行李,交了行李费5元。
(1)若京京带了84千克的行李,则该交行李费多少元?
(2)旅客最多可免费携带多少千克的行李?
五、(每小题10分,共20分)
19、如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm。
(1)求BE的长;
(2)当AD=4cm时,求四边形BDAE的面积。
20、如图,在平面直角坐标系xOy中,一次函数与x轴、y轴分别相交于点A和点B,直线经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求△ABO的面积;
(2)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式。
B卷(共50分)
一、填空题:(每小题4分,共20分)
21、若某数的平方根为 HYPERLINK "http://www./" 和,则 HYPERLINK "http://www./" =_________。
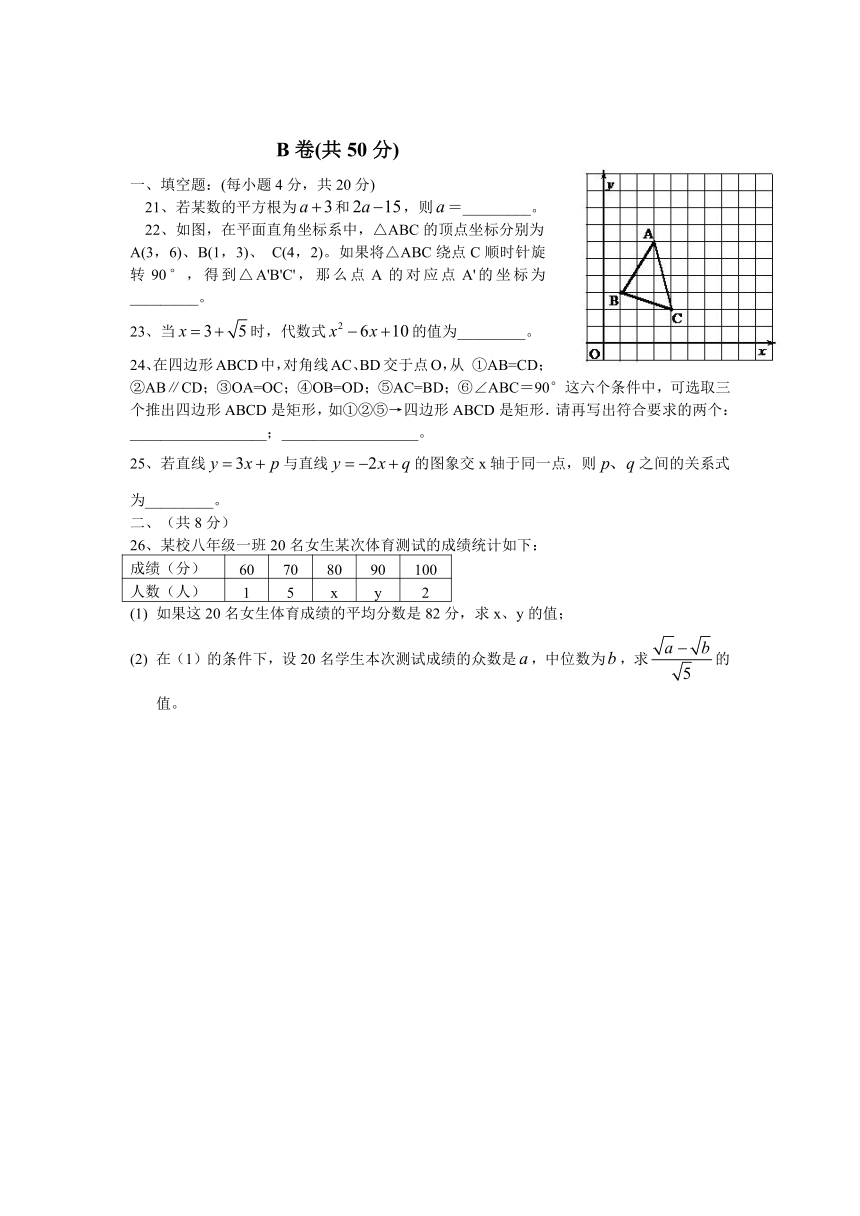
22、如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,6)、B(1,3)、 C(4,2)。如果将△ABC绕点C顺时针旋转90°,得到△A'B'C',那么点A的对应点A'的坐标为_________。
23、当时,代数式 HYPERLINK "http://www./" 的值为_________。
24、在四边形ABCD中,对角线AC、BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个:__________________;__________________。
25、若直线与直线 HYPERLINK "http://www./" 的图象交x轴于同一点,则之间的关系式为_________。
二、(共8分)
26、某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
如果这20名女生体育成绩的平均分数是82分,求x、y的值;
在(1)的条件下,设20名学生本次测试成绩的众数是 HYPERLINK "http://www./" ,中位数为,求的值。
三、(共10分)
27、如图①,在Rt△ABC中,已知∠A=90°,AB=AC,G、F分别是AB、AC上的两点,且GF∥BC,AF=2,BG=4。
(1)求梯形BCFG的面积;
(2)有一梯形DEFG与梯形BCFG重合,固定△ABC,将梯形DEFG向右运动,直到点D与点C重合为止,如图②.
①若某时段运动后形成的四边形BDG'G中,DG⊥BG',求运动路程BD的长,并求此时 HYPERLINK "http://www./" 的值;
②设运动中BD的长度为x,试用含x的代数式表示出梯形DEFG与Rt△ABC重合部分的面积S。
四、(共12分)
28、如图,在平面直角坐标系xOy中,已知直线PA是一次函数的图象,直线PB是一次函数 HYPERLINK "http://www./" 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点。
(1)用分别表示点A、B、P的坐标及∠PAB的度数;
(2)若四边形PQOB的面积是 HYPERLINK "http://www./" ,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;
(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由。
山东省青岛市2011—2012学年度第二学期八年级
下数学期末模拟试卷
答案:
A 卷(100分)
一、选择题:(每小题3分,共30分)
1.A; 2.C; 3.D;4.C; 5.B; 6.A; 7.D;8.C; 9.D; 10.C.
二、填空题:(每小题4分,共16分)
11.2; 12.20; 1 3.<; 1 4.1 20.
三、(第15题每小题6分,第16题6分,共18分)
15.(1)解:由①,得 …③ 1分
将③代人②,得.解得. 2分
将代人③,得. ……2分
∴该方程组的解为 ……1分
(2)解:原式= …4分
= ……2分
16.解:由题意,有, ……2分
解得. ……2分
∴. ……1分
∴.……1分
四、(每小题8分,共16分)
17.解:如图,由题意可得AF∥DC.∴∠AFE=∠DCE.
又∠AEF=∠DEC(对顶角相等),AE=DE(E为AD的中点), ……2分
∴△AEF≌△DEC(AAS). ……1分
∴AF=DC. ……1分
(2)矩形. ……1分
由(1),有AF=DC且AF∥DC。∴AFDC是平行四边形.……2分
又AD=CF,∴AFDC是矩形(对角线相等的平行四边形是矩形).……1分
18.解:(1)将代入了中,解得.……2分
∴一次函数的表达式为.……1分
将代入中,解得.
∴京京该交行李费9元. ……1分
(2)令,即,解得,解得.
∴旅客最多可免费携带30千克行李. ……3分
答:京京该交行李费9元,旅客最多可免费携带30千克行李。……1分
五、(每小题10分,共20分)
19.解:(1)由题意,有ED=DC,∠ADE=∠ADC=45°,∴∠EDC=90°. ……1分
又AD为△ABC的中线,∴CD,ED=DC=BD=3(cm). ……2分
在Rt△BDE中,由勾股定理,有(cm). ……2分
(2)在Rt△BDE中,∵BD=DE,∴∠EBD=45°.∴∠EBD=∠ADC=45°.
∴BE∥AD.∴BDAE是梯形. ……2分
过D作DF⊥BE于点F.
在Rt△BDE中,有
∴DF= (cm). ……1分
∴ ……2分
20.解:(1)在直线中,令,得. ∴B(0,2). ……1分
令,得. ∴A(3,0). ……2分
∴. ……2分
(2). ……1分
∵点P在第一象限,
∴.
解得. ……1分
而点P又在直线上,∴.解得.
∴P(). ……1分
将点C(1,0)、P(),代入中,有.∴
∴直线CP的函数表达式为. ……2分
B卷(共50分)
一、填空题:(每小题4分,共20分)
21.4;22.(8,3);23.6;24.①②⑥→四边形ABCD是矩形,③④⑤→四边形ABCD是矩形,
③④⑥→四边形AB(如是矩形(任选其中两个皆可);25. (或或).
二、(共8分)
26.解:(1)由题意,有 ……2分
解得 ……2分
(2)由(1),有众数,中位数. ……2分
∴ ……2分
三、(共10分)
27.解:(1)在Rt△ABC中,∵AB=AC,∴∠ABC=∠ACB=45°.又∵GF∥BC,∴∠AGF=∠AFG=45°.∴AG=AF=2,AB=AC=6. ……2分
∴. ……2分
(2)①∵在运动过程中有DG′∥BG且DG′=BG,∴BDG′G是平行四边形.
当DG⊥BG′时,BDG′G是菱形.∴BD=BG=4. ……2分
如图③,当BDG′G为菱形时,过点G′作G′M⊥BC于点M.
在Rt△G′DM中,∠G′DM=45°,DG′=4,∴DM=G′M且.
∴DM=G′M=,∴BM=.连接G′B.
在Rt△G′BM中,.……2分
②当o≤x≤时,其重合部分为梯形,如图②.
在Rt△AGF与Rt△ABC中,,.过G点作GH垂直BC于点H,得GH=.
由①,知BD=GG′=x,DC=,.
∴.……1分
当≤x≤时,其重合部分为等腰直角三角形,如图③.
∵斜边DC=,斜边上的高为,
∴.……1分
四、(共12分)
28.解:(1)在直线中,令,得. ∴点A(,0).……1分
在直线中,令,得. ∴点B(,o).……1分
由 得 ∴点P
在直线中,令,得,∴,即有AO=QO.
又∠AOQ=90°,∴∠PAB=45°. ……1分
(2)∵,,AO=CO,而CQ:AO=1:2
而 HYPERLINK "http://www./" .
过点P作PE垂直x轴于点E.
.
……2分
∴(舍去).得.∴P().
∴PA的函数表达式为,PB的函数表达式为. ……1分
(3)存在.
过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点,过点A作BP的平行线交PM于点,过点A、B分别作BP、AP的平行线交于点.
①∵∥AB且∥AP,∴是平行四边形.此时,易得;
②∵∥AB且∥BP,∴是平行四边形.此时,易得;
③∵∥AP且∥BP,此时是平行四边形.∵∥AP且B(2,O),∴。同理可得.
由 得 ∴ ……3分
甲
乙
丙
第9题图
下数学期末模拟试卷
A卷(共100分)
一、选择题:(本大题共有10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是正确的,把正确选项的代号填在题后的括号内.
1、排列做操队形时,甲、乙、丙位置如图所示,
甲对乙说,如果我的位置用(0,0)来表示,
你的位置用(2,1)表示,那么丙的位置是( )
(A)(5,4) (B)(4,5)
(C)(3,4) (D)(4、3)
2.4辆板车和5辆卡车一次能运27吨货,10辆
板车和3车卡车一次能运货20吨,设每辆板
车每次可运x吨货,每辆卡车每次能运y吨货,则可列方程组( )
(A) (B)
(C) (D)
3.能判定一个四边形是菱形的条件是( )
(A)对角线相等且互相垂直 (B)对角线相等且互相平分
(C)对角线互相垂直 (D)对角线互相垂直平分
4、在平面直角坐标系中,位于第二象限的点是( )
(A) (-2,-3) (B) (2,4) (C) (-2,3) (D) (2,3)
5、下列几组数据能作为直角三角形的三边长的是( )
(A) 2,3,4 (B) 5,3,4 (C) 4,6,9 (D) 5,11,13
6、已知是方程的一个解,那么 HYPERLINK "http://www./" 的值是( )
(A) 1 (B)3 (C)-3 (D) -1
7、下列图形中,既是轴对称又是中心对称的图形是( )
(A)正三角形 (B)平行四边形 (C)等腰梯形 (D)正方形
8、在平面直角坐标系中,直线不经过( )
(A)第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
9、如图,将一张矩形纸片对折后再对折,然后沿着图中的虚线剪下,得到①、②两部分,将②展开后得到的平面图形是( )
(A) 矩形 (B)平行四边形 (C)梯形 (D) 菱形
10、如图,再平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0)、(5,0)、(2,3),则顶点C的坐标是( ).
(A) (3,7) (B) (5,3) (C) (7,3) (D)(8,2)
二、填空题:(每小题4分,共16分)
11、若,那么 HYPERLINK "http://www./" =_________
12、若菱形的两条对角线长分别为6cm,8cm,则其周长为_________cm。
13、对于一次函数,如果 HYPERLINK "http://www./" ,那么(填“>”、“=”、“<”)。
14、如图是用形状、大小完全相同的等腰梯形密铺成的图案的一部分,则该图案中等腰梯形的较大内角的度数为_________度。
三、(第15题每小题6分,第16题6分,共18分)
15、解下列各题:
(1) 解方程组: HYPERLINK "http://www./"
(2)化简:
16、如果为的算术平方根,为 HYPERLINK "http://www./" 的立方根,求的平方根。
四、(每小题8分,共16分)
17、已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF。
求证:AF=DC;
若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论。
18、某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李票(元)与行李质量 HYPERLINK "http://www./" (千克)间的一次函数关系式为,现知贝贝带了60千克的行李,交了行李费5元。
(1)若京京带了84千克的行李,则该交行李费多少元?
(2)旅客最多可免费携带多少千克的行李?
五、(每小题10分,共20分)
19、如图,已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm。
(1)求BE的长;
(2)当AD=4cm时,求四边形BDAE的面积。
20、如图,在平面直角坐标系xOy中,一次函数与x轴、y轴分别相交于点A和点B,直线经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求△ABO的面积;
(2)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式。
B卷(共50分)
一、填空题:(每小题4分,共20分)
21、若某数的平方根为 HYPERLINK "http://www./" 和,则 HYPERLINK "http://www./" =_________。
22、如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,6)、B(1,3)、 C(4,2)。如果将△ABC绕点C顺时针旋转90°,得到△A'B'C',那么点A的对应点A'的坐标为_________。
23、当时,代数式 HYPERLINK "http://www./" 的值为_________。
24、在四边形ABCD中,对角线AC、BD交于点O,从 ①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤→四边形ABCD是矩形.请再写出符合要求的两个:__________________;__________________。
25、若直线与直线 HYPERLINK "http://www./" 的图象交x轴于同一点,则之间的关系式为_________。
二、(共8分)
26、某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
如果这20名女生体育成绩的平均分数是82分,求x、y的值;
在(1)的条件下,设20名学生本次测试成绩的众数是 HYPERLINK "http://www./" ,中位数为,求的值。
三、(共10分)
27、如图①,在Rt△ABC中,已知∠A=90°,AB=AC,G、F分别是AB、AC上的两点,且GF∥BC,AF=2,BG=4。
(1)求梯形BCFG的面积;
(2)有一梯形DEFG与梯形BCFG重合,固定△ABC,将梯形DEFG向右运动,直到点D与点C重合为止,如图②.
①若某时段运动后形成的四边形BDG'G中,DG⊥BG',求运动路程BD的长,并求此时 HYPERLINK "http://www./" 的值;
②设运动中BD的长度为x,试用含x的代数式表示出梯形DEFG与Rt△ABC重合部分的面积S。
四、(共12分)
28、如图,在平面直角坐标系xOy中,已知直线PA是一次函数的图象,直线PB是一次函数 HYPERLINK "http://www./" 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点。
(1)用分别表示点A、B、P的坐标及∠PAB的度数;
(2)若四边形PQOB的面积是 HYPERLINK "http://www./" ,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;
(3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由。
山东省青岛市2011—2012学年度第二学期八年级
下数学期末模拟试卷
答案:
A 卷(100分)
一、选择题:(每小题3分,共30分)
1.A; 2.C; 3.D;4.C; 5.B; 6.A; 7.D;8.C; 9.D; 10.C.
二、填空题:(每小题4分,共16分)
11.2; 12.20; 1 3.<; 1 4.1 20.
三、(第15题每小题6分,第16题6分,共18分)
15.(1)解:由①,得 …③ 1分
将③代人②,得.解得. 2分
将代人③,得. ……2分
∴该方程组的解为 ……1分
(2)解:原式= …4分
= ……2分
16.解:由题意,有, ……2分
解得. ……2分
∴. ……1分
∴.……1分
四、(每小题8分,共16分)
17.解:如图,由题意可得AF∥DC.∴∠AFE=∠DCE.
又∠AEF=∠DEC(对顶角相等),AE=DE(E为AD的中点), ……2分
∴△AEF≌△DEC(AAS). ……1分
∴AF=DC. ……1分
(2)矩形. ……1分
由(1),有AF=DC且AF∥DC。∴AFDC是平行四边形.……2分
又AD=CF,∴AFDC是矩形(对角线相等的平行四边形是矩形).……1分
18.解:(1)将代入了中,解得.……2分
∴一次函数的表达式为.……1分
将代入中,解得.
∴京京该交行李费9元. ……1分
(2)令,即,解得,解得.
∴旅客最多可免费携带30千克行李. ……3分
答:京京该交行李费9元,旅客最多可免费携带30千克行李。……1分
五、(每小题10分,共20分)
19.解:(1)由题意,有ED=DC,∠ADE=∠ADC=45°,∴∠EDC=90°. ……1分
又AD为△ABC的中线,∴CD,ED=DC=BD=3(cm). ……2分
在Rt△BDE中,由勾股定理,有(cm). ……2分
(2)在Rt△BDE中,∵BD=DE,∴∠EBD=45°.∴∠EBD=∠ADC=45°.
∴BE∥AD.∴BDAE是梯形. ……2分
过D作DF⊥BE于点F.
在Rt△BDE中,有
∴DF= (cm). ……1分
∴ ……2分
20.解:(1)在直线中,令,得. ∴B(0,2). ……1分
令,得. ∴A(3,0). ……2分
∴. ……2分
(2). ……1分
∵点P在第一象限,
∴.
解得. ……1分
而点P又在直线上,∴.解得.
∴P(). ……1分
将点C(1,0)、P(),代入中,有.∴
∴直线CP的函数表达式为. ……2分
B卷(共50分)
一、填空题:(每小题4分,共20分)
21.4;22.(8,3);23.6;24.①②⑥→四边形ABCD是矩形,③④⑤→四边形ABCD是矩形,
③④⑥→四边形AB(如是矩形(任选其中两个皆可);25. (或或).
二、(共8分)
26.解:(1)由题意,有 ……2分
解得 ……2分
(2)由(1),有众数,中位数. ……2分
∴ ……2分
三、(共10分)
27.解:(1)在Rt△ABC中,∵AB=AC,∴∠ABC=∠ACB=45°.又∵GF∥BC,∴∠AGF=∠AFG=45°.∴AG=AF=2,AB=AC=6. ……2分
∴. ……2分
(2)①∵在运动过程中有DG′∥BG且DG′=BG,∴BDG′G是平行四边形.
当DG⊥BG′时,BDG′G是菱形.∴BD=BG=4. ……2分
如图③,当BDG′G为菱形时,过点G′作G′M⊥BC于点M.
在Rt△G′DM中,∠G′DM=45°,DG′=4,∴DM=G′M且.
∴DM=G′M=,∴BM=.连接G′B.
在Rt△G′BM中,.……2分
②当o≤x≤时,其重合部分为梯形,如图②.
在Rt△AGF与Rt△ABC中,,.过G点作GH垂直BC于点H,得GH=.
由①,知BD=GG′=x,DC=,.
∴.……1分
当≤x≤时,其重合部分为等腰直角三角形,如图③.
∵斜边DC=,斜边上的高为,
∴.……1分
四、(共12分)
28.解:(1)在直线中,令,得. ∴点A(,0).……1分
在直线中,令,得. ∴点B(,o).……1分
由 得 ∴点P
在直线中,令,得,∴,即有AO=QO.
又∠AOQ=90°,∴∠PAB=45°. ……1分
(2)∵,,AO=CO,而CQ:AO=1:2
而 HYPERLINK "http://www./" .
过点P作PE垂直x轴于点E.
.
……2分
∴(舍去).得.∴P().
∴PA的函数表达式为,PB的函数表达式为. ……1分
(3)存在.
过点P作直线PM平行于x轴,过点B作AP的平行线交PM于点,过点A作BP的平行线交PM于点,过点A、B分别作BP、AP的平行线交于点.
①∵∥AB且∥AP,∴是平行四边形.此时,易得;
②∵∥AB且∥BP,∴是平行四边形.此时,易得;
③∵∥AP且∥BP,此时是平行四边形.∵∥AP且B(2,O),∴。同理可得.
由 得 ∴ ……3分
甲
乙
丙
第9题图
同课章节目录
