2021-2022学年人教版七年级数学上册4.3.2 角的比较与运算同步经典题精练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册4.3.2 角的比较与运算同步经典题精练(Word版,附答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览





文档简介
2021-2022学年上学期初中数学人教新版七年级同步经典题精练之角的认识与运算
一、选择题(共8小题)
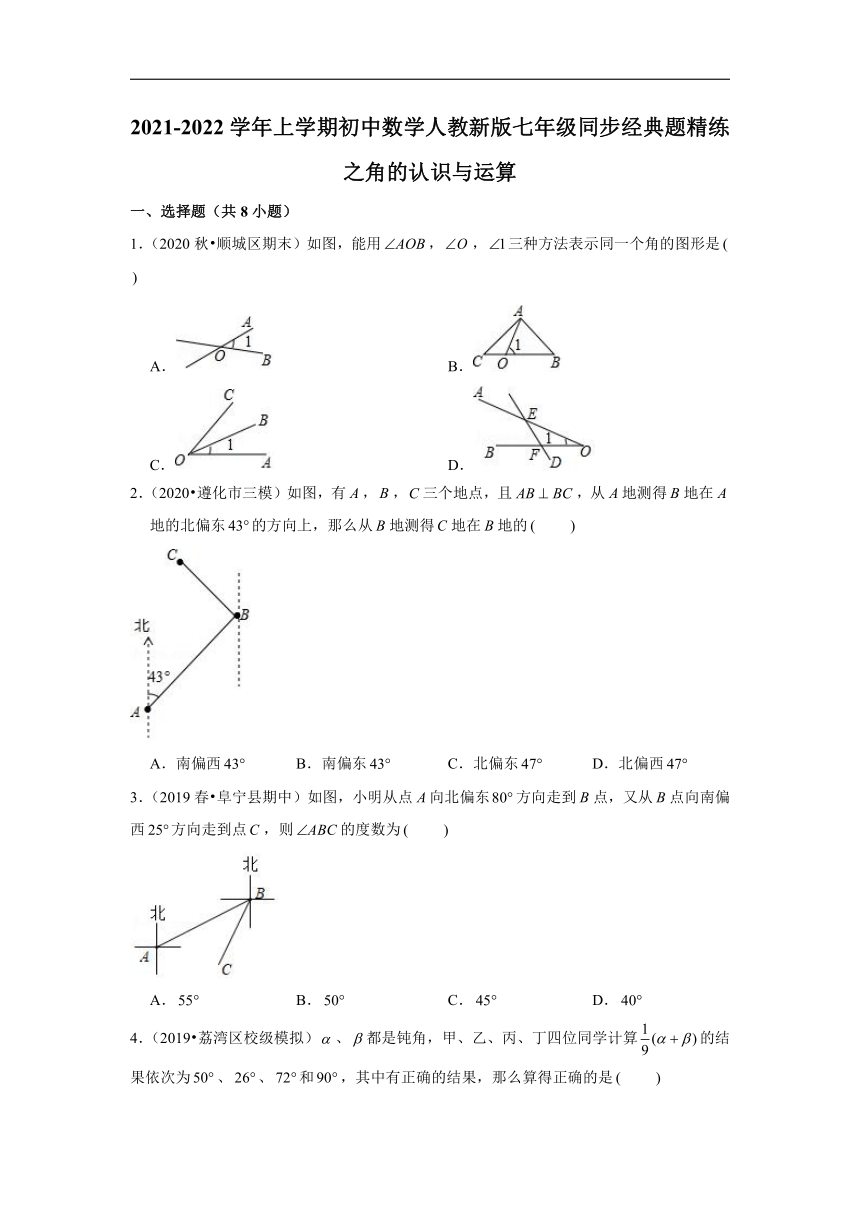
1.(2020秋?顺城区期末)如图,能用,,三种方法表示同一个角的图形是
A.
B.
C.
D.
2.(2020?遵化市三模)如图,有,,三个地点,且,从地测得地在地的北偏东的方向上,那么从地测得地在地的
A.南偏西
B.南偏东
C.北偏东
D.北偏西
3.(2019春?阜宁县期中)如图,小明从点向北偏东方向走到点,又从点向南偏西方向走到点,则的度数为
A.
B.
C.
D.
4.(2019?荔湾区校级模拟)、都是钝角,甲、乙、丙、丁四位同学计算的结果依次为、、和,其中有正确的结果,那么算得正确的是
A.甲
B.乙
C.丙
D.丁
5.(2018秋?渝北区期末)如图,张老师在点处观测到小明站位点位于北偏西的方向,同时观测到小刚站在点在南偏东的方向,那么的大小是
A.
B.
C.
D.
6.(2018秋?汝州市期末)已知:,,,下列结论正确的是
A.
B.
C.
D.三个角互不相等
7.(2018秋?罗庄区期末)时钟在2时40分时,时针与分针所夹的角的度数是
A.
B.
C.
D.
8.(2018秋?金东区期末)借助一副三角尺,你能画出下面哪个度数的角
A.
B.
C.
D.
二、填空题(共6小题)
9.(2018秋?永新县期末)已知和是共顶点的两个角,的边始终在的内部,并且的边把分为的两个角,若,,则的度数是 .
10.(2018秋?宿松县期末)如图,是线段上一点,连,用不等号“”表示与的大小关系为 .
11.(2018秋?蓝山县期末)王老师每晚都要看央视的“新闻联播”节目,这一时刻钟面上时针与分针的夹角是
度.
12.(2018秋?嘉陵区期末)如图,线段条数为,小于平角的角的个数为,则 .
13.(2018秋?定安县期末)如图,、分别是、的平分线,,则 度.
14.(2018秋?安顺期末)如图,甲从点出发向北偏东方向走至点,乙从出发向南偏西方向走至点,则的度数是
.
三、解答题(共6小题)
15.(2019春?成都期末)林湾乡修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村水渠从村沿什么方向修建,可以保持与的方向一致?
16.(2018秋?榆次区期末)如图所示,平分,分成的两部分,,求的度数.
17.(2018秋?会昌县期末)如图,一副三角板的两个直角顶点重合在一起.
(1)若,求的度数;
(2)比较与的大小,并写出理由.
18.(2018秋?庐江县期末)如图,是的平分线,是的平分线.
(1)如图1,当是直角,时,的度数是多少?
(2)如图2,当,时,猜想与的数量关系;
(3)如图3,当,时,猜想:与、有数量关系吗?如果有,指出结论并说明理由.
19.(2018秋?嘉祥县期末)如图,射线的方向是北偏东,射线的方向是北偏西,,射线是的反向延长线.
(1)射线的方向是 ;
(2)若射线平分,求的度数;
(3)直接写出一对互余的角是 ,一对互补的角是 .
20.(2018秋?大同期末)阅读并填空
问题:在一条直线上有,,,四个点,那么这条直线上总共有多少条线段?要解决这个问题,我们可以这样考虑,以为端点的线段有,,条,同样以为端点,以为端点,以为端点的线段也各有3条,这样共有4个3,即(条,但和是同一条线段,即每一条线段重复一次,所以一共有条线段.那么,如果在一条直线上有5个点,则这条直线上共有 条线段.如果在一条直线上有个点,那么这条直线上共有 条线段.
知识迁移:
如果在一个锐角内部画2条射线,,那么这个图形中总共有 个角,若在内画条射线,则总共有 个角.
学以致用:一段铁路上共有5个火车端,若一列客车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备 种不同的车票.
2021-2022学年上学期初中数学人教新版七年级同步经典题精练之角的认识与运算
参考答案与试题解析
一、选择题(共8小题)
1.(2020秋?顺城区期末)如图,能用,,三种方法表示同一个角的图形是
A.
B.
C.
D.
【答案】
【考点】角的概念
【专题】线段、角、相交线与平行线
【分析】根据角的四种表示方法和具体要求回答即可.
【解答】解:、以为顶点的角不止一个,不能用表示,故选项错误;
、以为顶点的角不止一个,不能用表示,故选项错误;
、以为顶点的角不止一个,不能用表示,故选项错误;
、能用,,三种方法表示同一个角,故选项正确.
故选:.
【点评】本题考查了角的表示方法的应用,掌握角的表示方法是解题的关键.
2.(2020?遵化市三模)如图,有,,三个地点,且,从地测得地在地的北偏东的方向上,那么从地测得地在地的
A.南偏西
B.南偏东
C.北偏东
D.北偏西
【考点】:方向角
【专题】11:计算题
【分析】根据方向角的概念,和平行线的性质求解.
【解答】解:,
,
,
,
,
地在地的北偏西的方向上.
故选:.
【点评】本题主要考查了方位角,平行线的性质,正确的识别图形是解题的关键.
3.(2019春?阜宁县期中)如图,小明从点向北偏东方向走到点,又从点向南偏西方向走到点,则的度数为
A.
B.
C.
D.
【考点】:方向角
【专题】551:线段、角、相交线与平行线
【分析】根据题意画出方位角,利用平行线的性质和角的和差关系即可求解.
【解答】解:如图,,
,
,
,
,
即.
故选:.
【点评】考查了方向角,答此类题需要从运动的角度,正确画出方位角,根据平行线的性质解答即可.
4.(2019?荔湾区校级模拟)、都是钝角,甲、乙、丙、丁四位同学计算的结果依次为、、和,其中有正确的结果,那么算得正确的是
A.甲
B.乙
C.丙
D.丁
【考点】:角的计算
【专题】551:线段、角、相交线与平行线
【分析】根据钝角的取值范围,确定的取值范围,即可求解.
【解答】解:、都是钝角,
,,
,
在此范围内,
故选:.
【点评】本题考查角的分类,角的范围.能够准确用不等式确定的范围是解题的关键.
5.(2018秋?渝北区期末)如图,张老师在点处观测到小明站位点位于北偏西的方向,同时观测到小刚站在点在南偏东的方向,那么的大小是
A.
B.
C.
D.
【考点】:度分秒的换算;:方向角
【专题】66:运算能力;551:线段、角、相交线与平行线
【分析】根据角的和差关系可得,再计算即可.
【解答】解:由题意得:,
故选:.
【点评】此题主要考查了度分秒的换算,以及方向角,关键是掌握1度分,即,1分秒,即.
6.(2018秋?汝州市期末)已知:,,,下列结论正确的是
A.
B.
C.
D.三个角互不相等
【考点】:度分秒的换算
【分析】根据小单位华大单位除以进率,可得答案.
【解答】解:,
故选:.
【点评】本题考查了度分秒的换算,小单位华大单位除以进率是解题关键.
7.(2018秋?罗庄区期末)时钟在2时40分时,时针与分针所夹的角的度数是
A.
B.
C.
D.
【考点】:钟面角
【专题】551:线段、角、相交线与平行线;66:运算能力
【分析】根据分针每分钟转,时针每分钟转得到40分钟分针从数字12开始转了,时针从数字2开始转了,于是2时40分时,时针与分针所夹的角度等于.
【解答】解:2时40分时,分针从数字12开始转了,时针从数字2开始转了
所以2时40分时,时针与分针所夹的角度.
故选:.
【点评】本题考查了钟面角.解题的关键是明确钟面角:钟面被分成12大格,每大格;分针每分钟转,时针每分钟转.
8.(2018秋?金东区期末)借助一副三角尺,你能画出下面哪个度数的角
A.
B.
C.
D.
【考点】:角的计算
【分析】先了解一副三角尺有,,,,然后根据这些角的和差可画出是的倍数的角,则可得.
【解答】解:用一副三角尺,可以画出小于的角有:,,,,,,,,,,.
故选:.
【点评】本题考查了三角板的知识.注意在大于而小于的范围内,只要是的倍数角都可以用一副三角尺画出.
二、填空题(共6小题)
9.(2018秋?永新县期末)已知和是共顶点的两个角,的边始终在的内部,并且的边把分为的两个角,若,,则的度数是 或或 .
【考点】角的计算
【专题】线段、角、相交线与平行线;几何直观
【分析】根据角的和差和角的倍分关系即可得到结论.
【解答】解:如图1,,,把分为的两个角,
,
;
如图2,
,,把分为的两个角,
,
;
如图3,,,把分为的两个角,
,
;
如图4,
,,把分为的两个角,
,
;
综上所述,的度数是或或.
故答案为:或或.
【点评】本题考查了角的计算,熟练掌握角的和、差、倍分关系是解题的关键.
10.(2018秋?宿松县期末)如图,是线段上一点,连,用不等号“”表示与的大小关系为 .
【考点】:角的大小比较;:角的概念
【专题】64:几何直观;552:三角形
【分析】三角形的一个外角大于和它不相邻的任何一个内角.根据三角形外角的性质得出即可.
【解答】解:是的一个外角,
,
即,
故答案为:.
【点评】本题考查了三角形的外角的性质,能熟记三角形外角的性质的内容是解此题的关键,注意:三角形的一个外角大于任意一个和它不相邻的内角.
11.(2018秋?蓝山县期末)王老师每晚都要看央视的“新闻联播”节目,这一时刻钟面上时针与分针的夹角是 150 度.
【考点】:钟面角
【专题】11:计算题
【分析】画出草图,利用钟表表盘的特征解答.
【解答】解:,时针和分针中间相差5大格.
钟表12个数字,每相邻两个数字之间的夹角为,
分针与时针的夹角是,
故答案为:150.
【点评】此题考查的知识点是钟面角,用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为.
12.(2018秋?嘉陵区期末)如图,线段条数为,小于平角的角的个数为,则 15 .
【考点】:直线、射线、线段;:角的概念
【专题】551:线段、角、相交线与平行线;64:几何直观
【分析】有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.依据线段和角的概念进行判断.
【解答】解:由图可得,线段条数为7,小于平角的角的个数为8,
则,
故答案为:15.
【点评】本题主要考查了线段和角的概念,有公共端点是两条射线组成的图形叫做角.
13.(2018秋?定安县期末)如图,、分别是、的平分线,,则 90 度.
【考点】:角平分线的定义
【专题】551:线段、角、相交线与平行线
【分析】根据和分别是与的角平分线,从而可以求解.
【解答】解:、分别是、的平分线,
,,
,
.
故答案为:90.
【点评】本题主要考查了角平分线的性质,根据角平分线定义得出所求角,难度适中.
14.(2018秋?安顺期末)如图,甲从点出发向北偏东方向走至点,乙从出发向南偏西方向走至点,则的度数是 .
【考点】:方向角
【分析】根据方向角,可得、,根据角的和差,可得答案.
【解答】解:甲从点出发向北偏东方向走至点,乙从出发向南偏西方向走至点,
,,
,
,
故答案为:.
【点评】本题考查了方向角,利用了方向角的表示方法,角的和差.
三、解答题(共6小题)
15.(2019春?成都期末)林湾乡修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村水渠从村沿什么方向修建,可以保持与的方向一致?
【考点】:方向角
【分析】利用平行线的性质得出,可得,进而得出的度数即可得出答案.
【解答】解:如图所示:
由题意可得:,
当保持与的方向一致,
则,可得,
故,
则,
即从村沿北偏东方向修建,可以保持与的方向一致.
【点评】此题主要考查了方向角以及平行线的性质,得出的度数是解题关键.
16.(2018秋?榆次区期末)如图所示,平分,分成的两部分,,求的度数.
【考点】:角平分线的定义
【专题】11:计算题
【分析】此题的关键是要先设的度数.然后再利用题中的关系求出,的值,让它与列成等式.从而求出的度数.
【解答】解:设,则,
得
答:.
【点评】此题的关键是设未知数,然后找出题中的等量关系解未知数.
17.(2018秋?会昌县期末)如图,一副三角板的两个直角顶点重合在一起.
(1)若,求的度数;
(2)比较与的大小,并写出理由.
【答案】(1);
(2),理由见解答过程.
【考点】余角和补角;角的大小比较
【专题】线段、角、相交线与平行线;几何直观
【分析】(1)根据和都为进行计算;
(2)利用同角的余角相等可以得与的大小关系.
【解答】解:(1),,
,
,
;
(2),理由:
,
,
.
【点评】本题考查了余角的定义和性质,关键是明确同角的余角相等,灵活运用角的和差关系进行计算.
18.(2018秋?庐江县期末)如图,是的平分线,是的平分线.
(1)如图1,当是直角,时,的度数是多少?
(2)如图2,当,时,猜想与的数量关系;
(3)如图3,当,时,猜想:与、有数量关系吗?如果有,指出结论并说明理由.
【考点】角平分线的定义;角的计算
【专题】线段、角、相交线与平行线
【分析】(1)求出度数,求出和的度数,代入求出即可;
(2)求出度数,求出和的度数,代入求出即可;
(3)求出度数,求出和的度数,代入求出即可.
【解答】解:(1)如图1,,,
,
平分,平分,
,
.
(2)如图2,,
理由是:,,
,
平分,平分,
,
.
(3)如图3,,与的大小无关.
理由:,,
.
是的平分线,是的平分线,
,
,
.
即.
【点评】本题考查了角平分线定义和角的有关计算,关键是求出、、的度数和得出.
19.(2018秋?嘉祥县期末)如图,射线的方向是北偏东,射线的方向是北偏西,,射线是的反向延长线.
(1)射线的方向是 北偏东 ;
(2)若射线平分,求的度数;
(3)直接写出一对互余的角是 ,一对互补的角是 .
【考点】:角平分线的定义;:余角和补角;:方向角
【专题】551:线段、角、相交线与平行线
【分析】(1)先求出,再求得的度数,即可确定的方向;
(2)根据射线平分,即可求出再利用求出答案即可;
(3)根据余角和补角的定义即可得到结论.
【解答】解:(1)的方向是北偏西,的方向是北偏东,
,,
,
,
,
,
的方向是北偏东;
故答案为:北偏东;
(2),,
,
又射线是的反向延长线,
,
,
平分,
.
,
;
(3),,
一对互余的角是与,一对互补的角是与.
故答案为:与,与.
【点评】此题主要考查了方向角的表达即方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南偏东(西多少度.
20.(2018秋?大同期末)阅读并填空
问题:在一条直线上有,,,四个点,那么这条直线上总共有多少条线段?要解决这个问题,我们可以这样考虑,以为端点的线段有,,条,同样以为端点,以为端点,以为端点的线段也各有3条,这样共有4个3,即(条,但和是同一条线段,即每一条线段重复一次,所以一共有条线段.那么,如果在一条直线上有5个点,则这条直线上共有 10 条线段.如果在一条直线上有个点,那么这条直线上共有 条线段.
知识迁移:
如果在一个锐角内部画2条射线,,那么这个图形中总共有 个角,若在内画条射线,则总共有 个角.
学以致用:一段铁路上共有5个火车端,若一列客车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备 种不同的车票.
【考点】列代数式;规律型:图形的变化类;直线、射线、线段;直线的性质:两点确定一条直线;角的概念
【专题】线段、角、相交线与平行线
【分析】问题:根据线段的定义解答;
知识迁移:根据角的定义解答;
学以致用:先计算出线段的条数,再根据两站之间需要两种车票解答.
【解答】解:问题:如果在一条直线上有5个点,则这条直线上共有条线段.如果在一条直线上有个点,那么这条直线上共有条线段.;
知识迁移:在内部画2条射线,,则图中有6个不同的角,在内部画条射线,,,,则图中有个不同的角;
学以致用:5个火车站代表的所有线段的条数,
需要车票的种数:(种.
故答案为:10,,6,,20.
【点评】此题主要考查了线段的计数问题,解本题的关键是找出规律,此类题目容易数重或遗漏,要特别注意.
考点卡片
1.列代数式
(1)定义:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
(2)列代数式五点注意:①仔细辨别词义.
列代数式时,要先认真审题,抓住关键词语,仔细辩析词义.如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分.
②分清数量关系.要正确列代数式,只有分清数量之间的关系.
③注意运算顺序.列代数式时,一般应在语言叙述的数量关系中,先读的先写,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来.④规范书写格式.列代数时要按要求规范地书写.像数字与字母、字母与字母相乘可省略乘号不写,数与数相乘必须写乘号;除法可写成分数形式,带分数与字母相乘需把代分数化为假分数,书写单位名称什么时不加括号,什么时要加括号.注意代数式括号的适当运用.
⑤正确进行代换.列代数式时,有时需将题中的字母代入公式,这就要求正确进行代换.
【规律方法】列代数式应该注意的四个问题
1.在同一个式子或具体问题中,每一个字母只能代表一个量.
2.要注意书写的规范性.用字母表示数以后,在含有字母与数字的乘法中,通常将“×”简写作“?”或者省略不写.
3.在数和表示数的字母乘积中,一般把数写在字母的前面,这个数若是带分数要把它化成假分数.
4.含有字母的除法,一般不用“÷”(除号),而是写成分数的形式.
2.规律型:图形的变化类
图形的变化类的规律题
首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
3.直线、射线、线段
(1)直线、射线、线段的表示方法
①直线:用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB.
②射线:是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边.
③线段:线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).
(2)点与直线的位置关系:①点经过直线,说明点在直线上;②点不经过直线,说明点在直线外.
4.直线的性质:两点确定一条直线
(1)直线公理:经过两点有且只有一条直线.
简称:两点确定一条直线.
(2)经过一点的直线有无数条,过两点就唯一确定,过三点就不一定了.
5.角的概念
(1)角的定义:有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.
(2)角的表示方法:角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母(如∠α,∠β,∠γ、…)表示,或用阿拉伯数字(∠1,∠2…)表示.
(3)平角、周角:角也可以看作是由一条射线绕它的端点旋转而形成的图形,当始边与终边成一条直线时形成平角,当始
边与终边旋转重合时,形成周角.
(4)角的度量:度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
6.钟面角
(1)钟面一周平均分60格,相邻两格刻度之间的时间间隔是1分钟,时针1分钟走格,分针1分钟走1格.钟面上每一格的度数为360°÷12=30°.
(2)计算钟面上时针与分针所成角的度数,一般先从钟面上找出某一时刻分针与时针所处的位置,确定其夹角,再根据表面上每一格30°的规律,计算出分针与时针的夹角的度数.
(3)钟面上的路程问题
分针:60分钟转一圈,每分钟转动的角度为:360°÷60=6°
时针:12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°.
7.方向角
方向角是从正北或正南方向到目标方向所形成的小于90°的角
(1)方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
(2)用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
(3)画方向角
以正南或正北方向作方向角的始边,另一边则表示对象所处的方向的射线.
8.度分秒的换算
(1)度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
(2)具体换算可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60.同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
9.角平分线的定义
(1)角平分线的定义
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
(2)性质:若OC是∠AOB的平分线
则∠AOC=∠BOC=∠AOB或∠AOB=2∠AOC=2∠BOC.
(3)平分角的方法有很多,如度量法、折叠法、尺规作图法等,要注意积累,多动手实践.
10.角的计算
(1)角的和差倍分
①∠AOB是∠AOC和∠BOC的和,记作:∠AOB=∠AOC+∠BOC.∠AOC是∠AOB和∠BOC的差,记作:∠AOC=∠AOB﹣∠BOC.②若射线OC是∠AOB的三等分线,则∠AOB=3∠BOC或∠BOC=∠AOB.
(2)度、分、秒的加减运算.在进行度分秒的加减时,要将度与度,分与分,秒与秒相加减,分秒相加,逢60要进位,相减时,要借1化60.
(3)度、分、秒的乘除运算.①乘法:度、分、秒分别相乘,结果逢60要进位.②除法:度、分、秒分别去除,把每一次的余数化作下一级单位进一步去除.
11.余角和补角
(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
(3)性质:等角的补角相等.等角的余角相等.
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联.
注意:余角(补角)与这两个角的位置没有关系.不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系.
12.角的大小比较
(1)比较角的大小有两种方法:
①测量法,即用量角器量角的度数,角的度数越大,角越大.
②叠合法,即将两个角叠合在一起比较,使两个角的顶点及一边重合,观察另一边的位置.
(2)表示法:
①∠AOB>∠A′O′B′,
②∠AOB=∠A′O′B′,
③∠AOB<∠A′O′B′.
一、选择题(共8小题)
1.(2020秋?顺城区期末)如图,能用,,三种方法表示同一个角的图形是
A.
B.
C.
D.
2.(2020?遵化市三模)如图,有,,三个地点,且,从地测得地在地的北偏东的方向上,那么从地测得地在地的
A.南偏西
B.南偏东
C.北偏东
D.北偏西
3.(2019春?阜宁县期中)如图,小明从点向北偏东方向走到点,又从点向南偏西方向走到点,则的度数为
A.
B.
C.
D.
4.(2019?荔湾区校级模拟)、都是钝角,甲、乙、丙、丁四位同学计算的结果依次为、、和,其中有正确的结果,那么算得正确的是
A.甲
B.乙
C.丙
D.丁
5.(2018秋?渝北区期末)如图,张老师在点处观测到小明站位点位于北偏西的方向,同时观测到小刚站在点在南偏东的方向,那么的大小是
A.
B.
C.
D.
6.(2018秋?汝州市期末)已知:,,,下列结论正确的是
A.
B.
C.
D.三个角互不相等
7.(2018秋?罗庄区期末)时钟在2时40分时,时针与分针所夹的角的度数是
A.
B.
C.
D.
8.(2018秋?金东区期末)借助一副三角尺,你能画出下面哪个度数的角
A.
B.
C.
D.
二、填空题(共6小题)
9.(2018秋?永新县期末)已知和是共顶点的两个角,的边始终在的内部,并且的边把分为的两个角,若,,则的度数是 .
10.(2018秋?宿松县期末)如图,是线段上一点,连,用不等号“”表示与的大小关系为 .
11.(2018秋?蓝山县期末)王老师每晚都要看央视的“新闻联播”节目,这一时刻钟面上时针与分针的夹角是
度.
12.(2018秋?嘉陵区期末)如图,线段条数为,小于平角的角的个数为,则 .
13.(2018秋?定安县期末)如图,、分别是、的平分线,,则 度.
14.(2018秋?安顺期末)如图,甲从点出发向北偏东方向走至点,乙从出发向南偏西方向走至点,则的度数是
.
三、解答题(共6小题)
15.(2019春?成都期末)林湾乡修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村水渠从村沿什么方向修建,可以保持与的方向一致?
16.(2018秋?榆次区期末)如图所示,平分,分成的两部分,,求的度数.
17.(2018秋?会昌县期末)如图,一副三角板的两个直角顶点重合在一起.
(1)若,求的度数;
(2)比较与的大小,并写出理由.
18.(2018秋?庐江县期末)如图,是的平分线,是的平分线.
(1)如图1,当是直角,时,的度数是多少?
(2)如图2,当,时,猜想与的数量关系;
(3)如图3,当,时,猜想:与、有数量关系吗?如果有,指出结论并说明理由.
19.(2018秋?嘉祥县期末)如图,射线的方向是北偏东,射线的方向是北偏西,,射线是的反向延长线.
(1)射线的方向是 ;
(2)若射线平分,求的度数;
(3)直接写出一对互余的角是 ,一对互补的角是 .
20.(2018秋?大同期末)阅读并填空
问题:在一条直线上有,,,四个点,那么这条直线上总共有多少条线段?要解决这个问题,我们可以这样考虑,以为端点的线段有,,条,同样以为端点,以为端点,以为端点的线段也各有3条,这样共有4个3,即(条,但和是同一条线段,即每一条线段重复一次,所以一共有条线段.那么,如果在一条直线上有5个点,则这条直线上共有 条线段.如果在一条直线上有个点,那么这条直线上共有 条线段.
知识迁移:
如果在一个锐角内部画2条射线,,那么这个图形中总共有 个角,若在内画条射线,则总共有 个角.
学以致用:一段铁路上共有5个火车端,若一列客车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备 种不同的车票.
2021-2022学年上学期初中数学人教新版七年级同步经典题精练之角的认识与运算
参考答案与试题解析
一、选择题(共8小题)
1.(2020秋?顺城区期末)如图,能用,,三种方法表示同一个角的图形是
A.
B.
C.
D.
【答案】
【考点】角的概念
【专题】线段、角、相交线与平行线
【分析】根据角的四种表示方法和具体要求回答即可.
【解答】解:、以为顶点的角不止一个,不能用表示,故选项错误;
、以为顶点的角不止一个,不能用表示,故选项错误;
、以为顶点的角不止一个,不能用表示,故选项错误;
、能用,,三种方法表示同一个角,故选项正确.
故选:.
【点评】本题考查了角的表示方法的应用,掌握角的表示方法是解题的关键.
2.(2020?遵化市三模)如图,有,,三个地点,且,从地测得地在地的北偏东的方向上,那么从地测得地在地的
A.南偏西
B.南偏东
C.北偏东
D.北偏西
【考点】:方向角
【专题】11:计算题
【分析】根据方向角的概念,和平行线的性质求解.
【解答】解:,
,
,
,
,
地在地的北偏西的方向上.
故选:.
【点评】本题主要考查了方位角,平行线的性质,正确的识别图形是解题的关键.
3.(2019春?阜宁县期中)如图,小明从点向北偏东方向走到点,又从点向南偏西方向走到点,则的度数为
A.
B.
C.
D.
【考点】:方向角
【专题】551:线段、角、相交线与平行线
【分析】根据题意画出方位角,利用平行线的性质和角的和差关系即可求解.
【解答】解:如图,,
,
,
,
,
即.
故选:.
【点评】考查了方向角,答此类题需要从运动的角度,正确画出方位角,根据平行线的性质解答即可.
4.(2019?荔湾区校级模拟)、都是钝角,甲、乙、丙、丁四位同学计算的结果依次为、、和,其中有正确的结果,那么算得正确的是
A.甲
B.乙
C.丙
D.丁
【考点】:角的计算
【专题】551:线段、角、相交线与平行线
【分析】根据钝角的取值范围,确定的取值范围,即可求解.
【解答】解:、都是钝角,
,,
,
在此范围内,
故选:.
【点评】本题考查角的分类,角的范围.能够准确用不等式确定的范围是解题的关键.
5.(2018秋?渝北区期末)如图,张老师在点处观测到小明站位点位于北偏西的方向,同时观测到小刚站在点在南偏东的方向,那么的大小是
A.
B.
C.
D.
【考点】:度分秒的换算;:方向角
【专题】66:运算能力;551:线段、角、相交线与平行线
【分析】根据角的和差关系可得,再计算即可.
【解答】解:由题意得:,
故选:.
【点评】此题主要考查了度分秒的换算,以及方向角,关键是掌握1度分,即,1分秒,即.
6.(2018秋?汝州市期末)已知:,,,下列结论正确的是
A.
B.
C.
D.三个角互不相等
【考点】:度分秒的换算
【分析】根据小单位华大单位除以进率,可得答案.
【解答】解:,
故选:.
【点评】本题考查了度分秒的换算,小单位华大单位除以进率是解题关键.
7.(2018秋?罗庄区期末)时钟在2时40分时,时针与分针所夹的角的度数是
A.
B.
C.
D.
【考点】:钟面角
【专题】551:线段、角、相交线与平行线;66:运算能力
【分析】根据分针每分钟转,时针每分钟转得到40分钟分针从数字12开始转了,时针从数字2开始转了,于是2时40分时,时针与分针所夹的角度等于.
【解答】解:2时40分时,分针从数字12开始转了,时针从数字2开始转了
所以2时40分时,时针与分针所夹的角度.
故选:.
【点评】本题考查了钟面角.解题的关键是明确钟面角:钟面被分成12大格,每大格;分针每分钟转,时针每分钟转.
8.(2018秋?金东区期末)借助一副三角尺,你能画出下面哪个度数的角
A.
B.
C.
D.
【考点】:角的计算
【分析】先了解一副三角尺有,,,,然后根据这些角的和差可画出是的倍数的角,则可得.
【解答】解:用一副三角尺,可以画出小于的角有:,,,,,,,,,,.
故选:.
【点评】本题考查了三角板的知识.注意在大于而小于的范围内,只要是的倍数角都可以用一副三角尺画出.
二、填空题(共6小题)
9.(2018秋?永新县期末)已知和是共顶点的两个角,的边始终在的内部,并且的边把分为的两个角,若,,则的度数是 或或 .
【考点】角的计算
【专题】线段、角、相交线与平行线;几何直观
【分析】根据角的和差和角的倍分关系即可得到结论.
【解答】解:如图1,,,把分为的两个角,
,
;
如图2,
,,把分为的两个角,
,
;
如图3,,,把分为的两个角,
,
;
如图4,
,,把分为的两个角,
,
;
综上所述,的度数是或或.
故答案为:或或.
【点评】本题考查了角的计算,熟练掌握角的和、差、倍分关系是解题的关键.
10.(2018秋?宿松县期末)如图,是线段上一点,连,用不等号“”表示与的大小关系为 .
【考点】:角的大小比较;:角的概念
【专题】64:几何直观;552:三角形
【分析】三角形的一个外角大于和它不相邻的任何一个内角.根据三角形外角的性质得出即可.
【解答】解:是的一个外角,
,
即,
故答案为:.
【点评】本题考查了三角形的外角的性质,能熟记三角形外角的性质的内容是解此题的关键,注意:三角形的一个外角大于任意一个和它不相邻的内角.
11.(2018秋?蓝山县期末)王老师每晚都要看央视的“新闻联播”节目,这一时刻钟面上时针与分针的夹角是 150 度.
【考点】:钟面角
【专题】11:计算题
【分析】画出草图,利用钟表表盘的特征解答.
【解答】解:,时针和分针中间相差5大格.
钟表12个数字,每相邻两个数字之间的夹角为,
分针与时针的夹角是,
故答案为:150.
【点评】此题考查的知识点是钟面角,用到的知识点为:钟表上12个数字,每相邻两个数字之间的夹角为.
12.(2018秋?嘉陵区期末)如图,线段条数为,小于平角的角的个数为,则 15 .
【考点】:直线、射线、线段;:角的概念
【专题】551:线段、角、相交线与平行线;64:几何直观
【分析】有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.依据线段和角的概念进行判断.
【解答】解:由图可得,线段条数为7,小于平角的角的个数为8,
则,
故答案为:15.
【点评】本题主要考查了线段和角的概念,有公共端点是两条射线组成的图形叫做角.
13.(2018秋?定安县期末)如图,、分别是、的平分线,,则 90 度.
【考点】:角平分线的定义
【专题】551:线段、角、相交线与平行线
【分析】根据和分别是与的角平分线,从而可以求解.
【解答】解:、分别是、的平分线,
,,
,
.
故答案为:90.
【点评】本题主要考查了角平分线的性质,根据角平分线定义得出所求角,难度适中.
14.(2018秋?安顺期末)如图,甲从点出发向北偏东方向走至点,乙从出发向南偏西方向走至点,则的度数是 .
【考点】:方向角
【分析】根据方向角,可得、,根据角的和差,可得答案.
【解答】解:甲从点出发向北偏东方向走至点,乙从出发向南偏西方向走至点,
,,
,
,
故答案为:.
【点评】本题考查了方向角,利用了方向角的表示方法,角的和差.
三、解答题(共6小题)
15.(2019春?成都期末)林湾乡修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村水渠从村沿什么方向修建,可以保持与的方向一致?
【考点】:方向角
【分析】利用平行线的性质得出,可得,进而得出的度数即可得出答案.
【解答】解:如图所示:
由题意可得:,
当保持与的方向一致,
则,可得,
故,
则,
即从村沿北偏东方向修建,可以保持与的方向一致.
【点评】此题主要考查了方向角以及平行线的性质,得出的度数是解题关键.
16.(2018秋?榆次区期末)如图所示,平分,分成的两部分,,求的度数.
【考点】:角平分线的定义
【专题】11:计算题
【分析】此题的关键是要先设的度数.然后再利用题中的关系求出,的值,让它与列成等式.从而求出的度数.
【解答】解:设,则,
得
答:.
【点评】此题的关键是设未知数,然后找出题中的等量关系解未知数.
17.(2018秋?会昌县期末)如图,一副三角板的两个直角顶点重合在一起.
(1)若,求的度数;
(2)比较与的大小,并写出理由.
【答案】(1);
(2),理由见解答过程.
【考点】余角和补角;角的大小比较
【专题】线段、角、相交线与平行线;几何直观
【分析】(1)根据和都为进行计算;
(2)利用同角的余角相等可以得与的大小关系.
【解答】解:(1),,
,
,
;
(2),理由:
,
,
.
【点评】本题考查了余角的定义和性质,关键是明确同角的余角相等,灵活运用角的和差关系进行计算.
18.(2018秋?庐江县期末)如图,是的平分线,是的平分线.
(1)如图1,当是直角,时,的度数是多少?
(2)如图2,当,时,猜想与的数量关系;
(3)如图3,当,时,猜想:与、有数量关系吗?如果有,指出结论并说明理由.
【考点】角平分线的定义;角的计算
【专题】线段、角、相交线与平行线
【分析】(1)求出度数,求出和的度数,代入求出即可;
(2)求出度数,求出和的度数,代入求出即可;
(3)求出度数,求出和的度数,代入求出即可.
【解答】解:(1)如图1,,,
,
平分,平分,
,
.
(2)如图2,,
理由是:,,
,
平分,平分,
,
.
(3)如图3,,与的大小无关.
理由:,,
.
是的平分线,是的平分线,
,
,
.
即.
【点评】本题考查了角平分线定义和角的有关计算,关键是求出、、的度数和得出.
19.(2018秋?嘉祥县期末)如图,射线的方向是北偏东,射线的方向是北偏西,,射线是的反向延长线.
(1)射线的方向是 北偏东 ;
(2)若射线平分,求的度数;
(3)直接写出一对互余的角是 ,一对互补的角是 .
【考点】:角平分线的定义;:余角和补角;:方向角
【专题】551:线段、角、相交线与平行线
【分析】(1)先求出,再求得的度数,即可确定的方向;
(2)根据射线平分,即可求出再利用求出答案即可;
(3)根据余角和补角的定义即可得到结论.
【解答】解:(1)的方向是北偏西,的方向是北偏东,
,,
,
,
,
,
的方向是北偏东;
故答案为:北偏东;
(2),,
,
又射线是的反向延长线,
,
,
平分,
.
,
;
(3),,
一对互余的角是与,一对互补的角是与.
故答案为:与,与.
【点评】此题主要考查了方向角的表达即方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南偏东(西多少度.
20.(2018秋?大同期末)阅读并填空
问题:在一条直线上有,,,四个点,那么这条直线上总共有多少条线段?要解决这个问题,我们可以这样考虑,以为端点的线段有,,条,同样以为端点,以为端点,以为端点的线段也各有3条,这样共有4个3,即(条,但和是同一条线段,即每一条线段重复一次,所以一共有条线段.那么,如果在一条直线上有5个点,则这条直线上共有 10 条线段.如果在一条直线上有个点,那么这条直线上共有 条线段.
知识迁移:
如果在一个锐角内部画2条射线,,那么这个图形中总共有 个角,若在内画条射线,则总共有 个角.
学以致用:一段铁路上共有5个火车端,若一列客车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备 种不同的车票.
【考点】列代数式;规律型:图形的变化类;直线、射线、线段;直线的性质:两点确定一条直线;角的概念
【专题】线段、角、相交线与平行线
【分析】问题:根据线段的定义解答;
知识迁移:根据角的定义解答;
学以致用:先计算出线段的条数,再根据两站之间需要两种车票解答.
【解答】解:问题:如果在一条直线上有5个点,则这条直线上共有条线段.如果在一条直线上有个点,那么这条直线上共有条线段.;
知识迁移:在内部画2条射线,,则图中有6个不同的角,在内部画条射线,,,,则图中有个不同的角;
学以致用:5个火车站代表的所有线段的条数,
需要车票的种数:(种.
故答案为:10,,6,,20.
【点评】此题主要考查了线段的计数问题,解本题的关键是找出规律,此类题目容易数重或遗漏,要特别注意.
考点卡片
1.列代数式
(1)定义:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.
(2)列代数式五点注意:①仔细辨别词义.
列代数式时,要先认真审题,抓住关键词语,仔细辩析词义.如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分.
②分清数量关系.要正确列代数式,只有分清数量之间的关系.
③注意运算顺序.列代数式时,一般应在语言叙述的数量关系中,先读的先写,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来.④规范书写格式.列代数时要按要求规范地书写.像数字与字母、字母与字母相乘可省略乘号不写,数与数相乘必须写乘号;除法可写成分数形式,带分数与字母相乘需把代分数化为假分数,书写单位名称什么时不加括号,什么时要加括号.注意代数式括号的适当运用.
⑤正确进行代换.列代数式时,有时需将题中的字母代入公式,这就要求正确进行代换.
【规律方法】列代数式应该注意的四个问题
1.在同一个式子或具体问题中,每一个字母只能代表一个量.
2.要注意书写的规范性.用字母表示数以后,在含有字母与数字的乘法中,通常将“×”简写作“?”或者省略不写.
3.在数和表示数的字母乘积中,一般把数写在字母的前面,这个数若是带分数要把它化成假分数.
4.含有字母的除法,一般不用“÷”(除号),而是写成分数的形式.
2.规律型:图形的变化类
图形的变化类的规律题
首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.
3.直线、射线、线段
(1)直线、射线、线段的表示方法
①直线:用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB.
②射线:是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边.
③线段:线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).
(2)点与直线的位置关系:①点经过直线,说明点在直线上;②点不经过直线,说明点在直线外.
4.直线的性质:两点确定一条直线
(1)直线公理:经过两点有且只有一条直线.
简称:两点确定一条直线.
(2)经过一点的直线有无数条,过两点就唯一确定,过三点就不一定了.
5.角的概念
(1)角的定义:有公共端点是两条射线组成的图形叫做角,其中这个公共端点是角的顶点,这两条射线是角的两条边.
(2)角的表示方法:角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母(如∠α,∠β,∠γ、…)表示,或用阿拉伯数字(∠1,∠2…)表示.
(3)平角、周角:角也可以看作是由一条射线绕它的端点旋转而形成的图形,当始边与终边成一条直线时形成平角,当始
边与终边旋转重合时,形成周角.
(4)角的度量:度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
6.钟面角
(1)钟面一周平均分60格,相邻两格刻度之间的时间间隔是1分钟,时针1分钟走格,分针1分钟走1格.钟面上每一格的度数为360°÷12=30°.
(2)计算钟面上时针与分针所成角的度数,一般先从钟面上找出某一时刻分针与时针所处的位置,确定其夹角,再根据表面上每一格30°的规律,计算出分针与时针的夹角的度数.
(3)钟面上的路程问题
分针:60分钟转一圈,每分钟转动的角度为:360°÷60=6°
时针:12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°.
7.方向角
方向角是从正北或正南方向到目标方向所形成的小于90°的角
(1)方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
(2)用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
(3)画方向角
以正南或正北方向作方向角的始边,另一边则表示对象所处的方向的射线.
8.度分秒的换算
(1)度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
(2)具体换算可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60.同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
9.角平分线的定义
(1)角平分线的定义
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
(2)性质:若OC是∠AOB的平分线
则∠AOC=∠BOC=∠AOB或∠AOB=2∠AOC=2∠BOC.
(3)平分角的方法有很多,如度量法、折叠法、尺规作图法等,要注意积累,多动手实践.
10.角的计算
(1)角的和差倍分
①∠AOB是∠AOC和∠BOC的和,记作:∠AOB=∠AOC+∠BOC.∠AOC是∠AOB和∠BOC的差,记作:∠AOC=∠AOB﹣∠BOC.②若射线OC是∠AOB的三等分线,则∠AOB=3∠BOC或∠BOC=∠AOB.
(2)度、分、秒的加减运算.在进行度分秒的加减时,要将度与度,分与分,秒与秒相加减,分秒相加,逢60要进位,相减时,要借1化60.
(3)度、分、秒的乘除运算.①乘法:度、分、秒分别相乘,结果逢60要进位.②除法:度、分、秒分别去除,把每一次的余数化作下一级单位进一步去除.
11.余角和补角
(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
(3)性质:等角的补角相等.等角的余角相等.
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联.
注意:余角(补角)与这两个角的位置没有关系.不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系.
12.角的大小比较
(1)比较角的大小有两种方法:
①测量法,即用量角器量角的度数,角的度数越大,角越大.
②叠合法,即将两个角叠合在一起比较,使两个角的顶点及一边重合,观察另一边的位置.
(2)表示法:
①∠AOB>∠A′O′B′,
②∠AOB=∠A′O′B′,
③∠AOB<∠A′O′B′.
