解直角三角形复习
图片预览


文档简介
(共20张PPT)
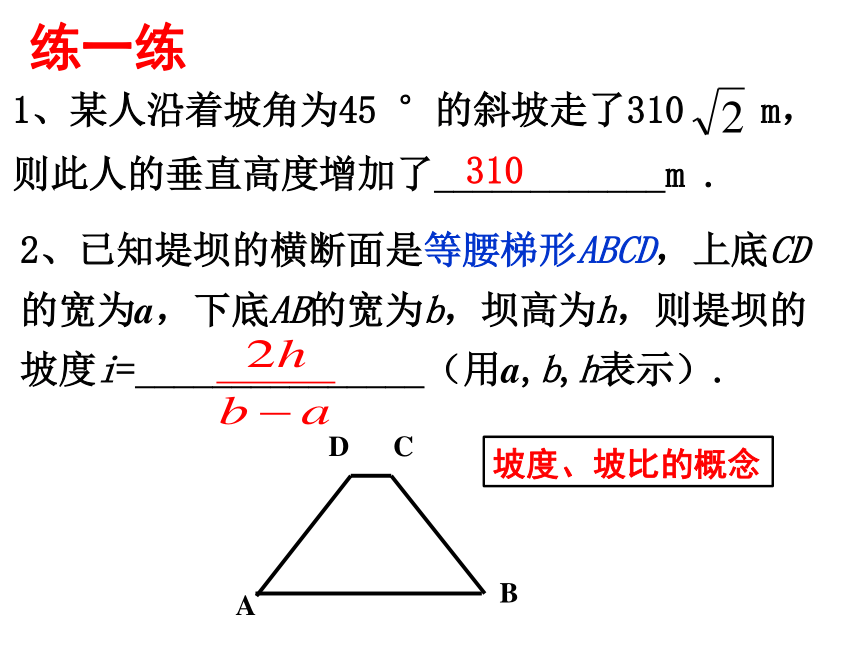
1、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m .
2、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示).
A
D
C
B
310
坡度、坡比的概念
练一练
3、cos2700+cos450·sin450+sin2700
变:sin2200+cos300·sin450+sin2700
变:sin210+sin220+…+sin2880+sin2890
练一练
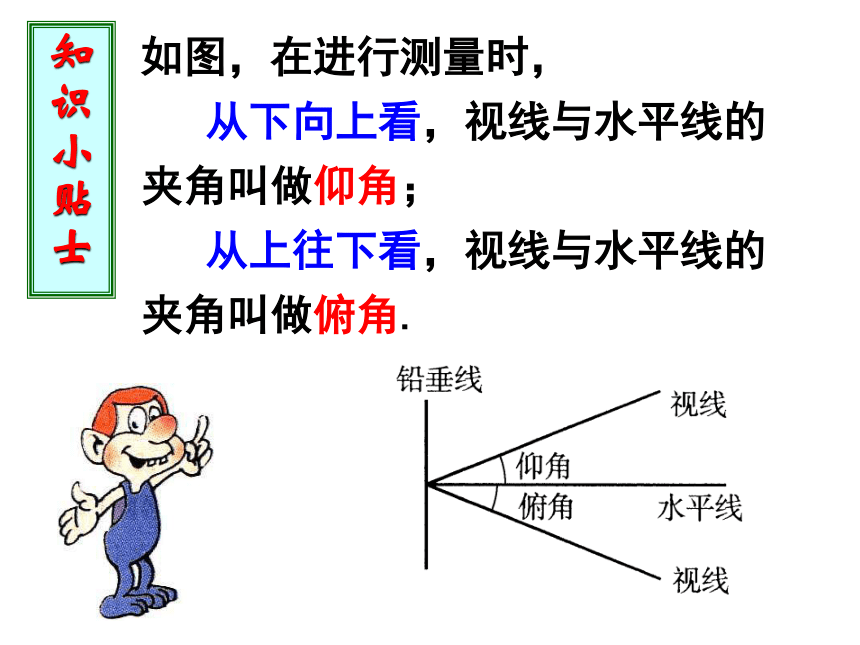
如图,在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
知识小贴士
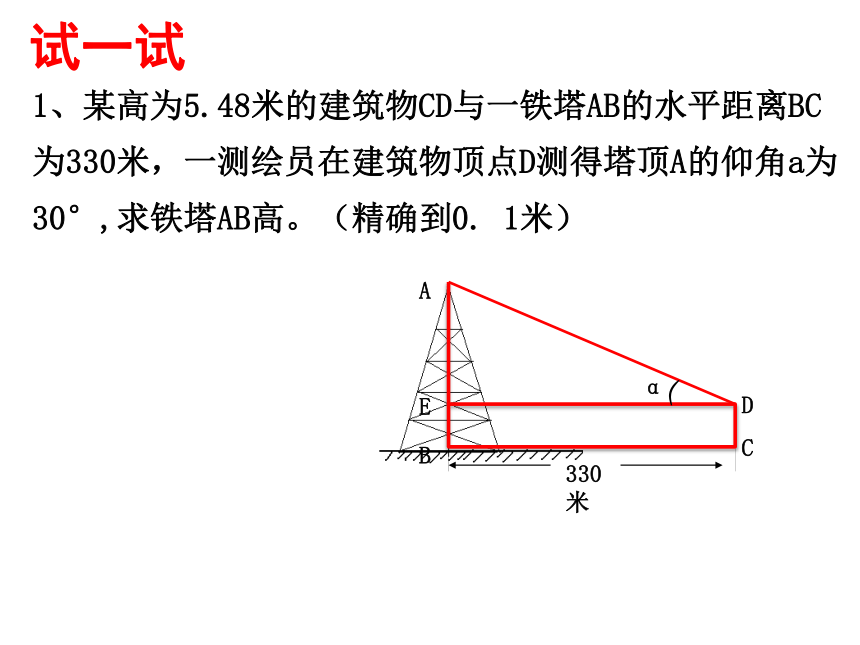
330米
A
B
C
D
E
α
︶
1、某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高。(精确到0. 1米)
试一试
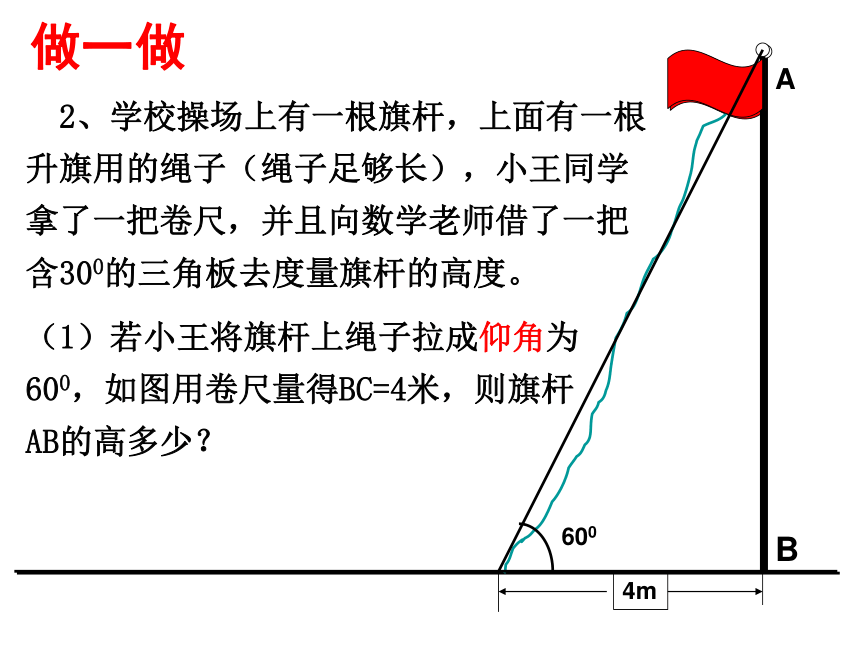
2、学校操场上有一根旗杆,上面有一根升旗用的绳子(绳子足够长),小王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若小王将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
A
B
4m
600
做一做
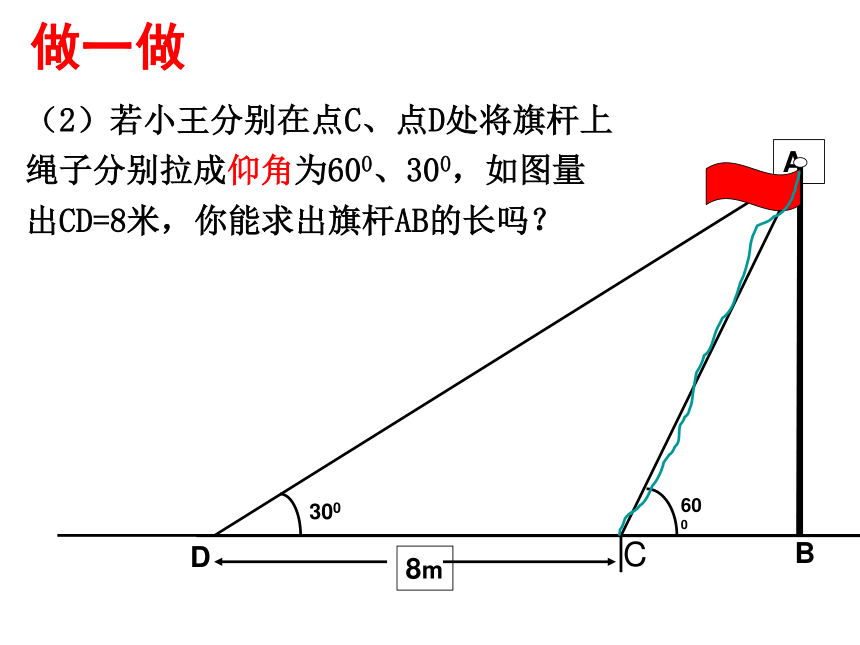
(2)若小王分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
A
B
D
8m
300
600
C
做一做
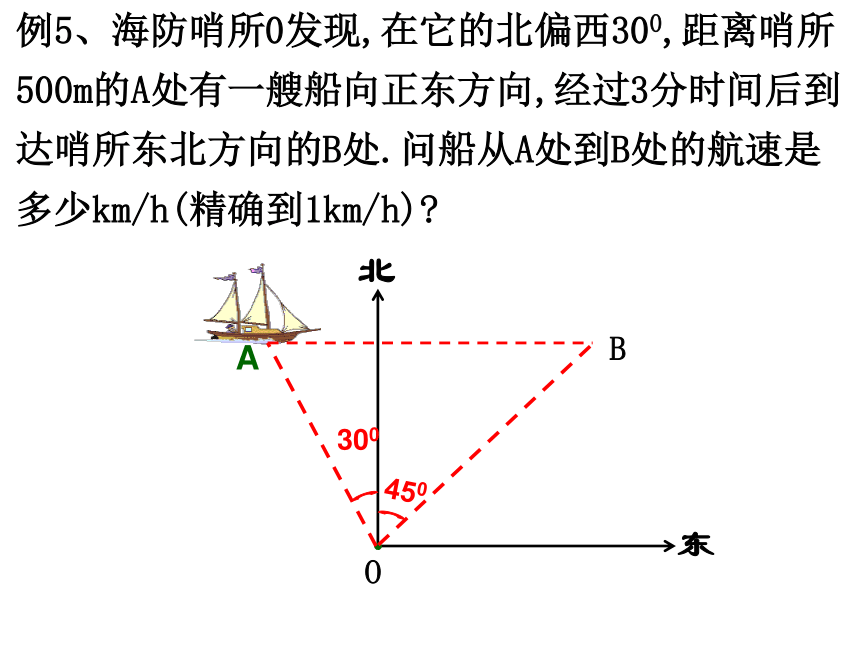
例5、海防哨所0发现,在它的北偏西300,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)
北
东
300
450
O
A
B
500
北
东
300
450
O
A
B
C
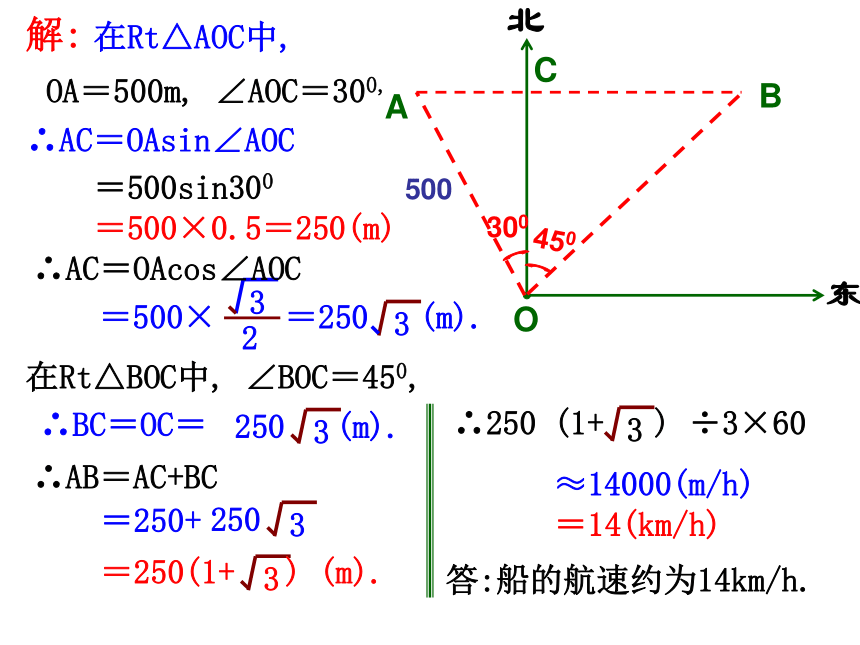
解:
在Rt△AOC中,
OA=500m, ∠AOC=300,
∴AC=OAsin∠AOC
=500sin300
=500× =250 (m).
3
2
3
在Rt△BOC中, ∠BOC=450,
=500×0.5=250(m)
∴AC=OAcos∠AOC
∴BC=OC=
250 (m).
3
∴AB=AC+BC
=250+
250
3
∴250 (1+ ) ÷3×60
3
3
=250(1+ ) (m).
≈14000(m/h)
=14(km/h)
答:船的航速约为14km/h.
模型一
模型二
模型三
模型四
例3:已知在△ABC中,sinA= ,AB=8,AC=6,
求△ABC的面积.
1、已知在△ABC中,AB+AC=9,AB和AC的夹角为30度,
设当AB=x时,△ABC面积为S
(1)求S关于x的函数解析式.
(2)问何时△ABC面积最大 最大面积是多少
提高题
许多有关图形的计算问题都可以直接,或通过添辅助线,化归为直角三角形问题来解决.
2、如图所示,在RT△ABC中,∠C=900,AC=8cm,BC=6cm,P点从B点出发,以2cm/s的速度向点A移动,Q点从A点出发以1cm/s的速度向C移动,P,Q同时出发,一点到达终点,另一点立即停止。设运动时间为t
(1)t为何值时,PQ∥BC
(2)t为何值,△APQ与△ABC相似
(3)设△APQ面积为s,求s关于t的函数关系式,并求自变量t的取值范围。
模型三
同类问题
优化122:5
优化123:8
例3:优化122页 例2
P
A
B
C
a
B
X
h
1、两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45度,测得低楼的底部C点的俯角为60度,求两楼的高度。
A
D
B
C
30米
450
600
练一练
2、为知道甲,乙两楼间的距离,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35012′,观测到乙楼底C的俯角为43024′.求这两楼的高度(精确到0.1m)
32.6
A
B
C
D
E
F
35°12′
43°24′
练一练
通过实践了解仰角和俯角在解直角三角形中的作用。
解直角三角形的应用是数学中的应用问题,反映现实领域特征的问题情景,它包含着一定的数学概念、方法和结果。
通过对实际问题的抽象提炼,分辨出解直角三角形的基本模式,用常规的代数方法解决问题。
船有无触礁的危险
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗
A
B
C
D
北
东
楼梯加长了多少
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
A
B
C
D
┌
1、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m .
2、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示).
A
D
C
B
310
坡度、坡比的概念
练一练
3、cos2700+cos450·sin450+sin2700
变:sin2200+cos300·sin450+sin2700
变:sin210+sin220+…+sin2880+sin2890
练一练
如图,在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
知识小贴士
330米
A
B
C
D
E
α
︶
1、某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高。(精确到0. 1米)
试一试
2、学校操场上有一根旗杆,上面有一根升旗用的绳子(绳子足够长),小王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若小王将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
A
B
4m
600
做一做
(2)若小王分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
A
B
D
8m
300
600
C
做一做
例5、海防哨所0发现,在它的北偏西300,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)
北
东
300
450
O
A
B
500
北
东
300
450
O
A
B
C
解:
在Rt△AOC中,
OA=500m, ∠AOC=300,
∴AC=OAsin∠AOC
=500sin300
=500× =250 (m).
3
2
3
在Rt△BOC中, ∠BOC=450,
=500×0.5=250(m)
∴AC=OAcos∠AOC
∴BC=OC=
250 (m).
3
∴AB=AC+BC
=250+
250
3
∴250 (1+ ) ÷3×60
3
3
=250(1+ ) (m).
≈14000(m/h)
=14(km/h)
答:船的航速约为14km/h.
模型一
模型二
模型三
模型四
例3:已知在△ABC中,sinA= ,AB=8,AC=6,
求△ABC的面积.
1、已知在△ABC中,AB+AC=9,AB和AC的夹角为30度,
设当AB=x时,△ABC面积为S
(1)求S关于x的函数解析式.
(2)问何时△ABC面积最大 最大面积是多少
提高题
许多有关图形的计算问题都可以直接,或通过添辅助线,化归为直角三角形问题来解决.
2、如图所示,在RT△ABC中,∠C=900,AC=8cm,BC=6cm,P点从B点出发,以2cm/s的速度向点A移动,Q点从A点出发以1cm/s的速度向C移动,P,Q同时出发,一点到达终点,另一点立即停止。设运动时间为t
(1)t为何值时,PQ∥BC
(2)t为何值,△APQ与△ABC相似
(3)设△APQ面积为s,求s关于t的函数关系式,并求自变量t的取值范围。
模型三
同类问题
优化122:5
优化123:8
例3:优化122页 例2
P
A
B
C
a
B
X
h
1、两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45度,测得低楼的底部C点的俯角为60度,求两楼的高度。
A
D
B
C
30米
450
600
练一练
2、为知道甲,乙两楼间的距离,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35012′,观测到乙楼底C的俯角为43024′.求这两楼的高度(精确到0.1m)
32.6
A
B
C
D
E
F
35°12′
43°24′
练一练
通过实践了解仰角和俯角在解直角三角形中的作用。
解直角三角形的应用是数学中的应用问题,反映现实领域特征的问题情景,它包含着一定的数学概念、方法和结果。
通过对实际问题的抽象提炼,分辨出解直角三角形的基本模式,用常规的代数方法解决问题。
船有无触礁的危险
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗
A
B
C
D
北
东
楼梯加长了多少
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
A
B
C
D
┌
