垂径定理

(共41张PPT)
海伦市共合镇中学 张利
1、我们所学的圆是不是轴对称图形呢？
圆是轴对称图形，经过圆心的每一条直线都是它们的对称轴
.
2、我们所学的圆是不是中心对称图形呢？
圆是中心对称图形，圆心是对称中心
问题 ：你知道赵州桥吗 它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶．它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？
赵州桥主桥拱的半径是多少？
如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？
（2）你能发现图中有那些相等的线段和弧？为什么？
·
O
A
B
C
D
E
活 动 一
（1）是轴对称图形．直径CD所在的直线是它的对称轴
（2） 线段： AE=BE
⌒
⌒
弧：ＡＣ＝ＢＣ　，ＡＤ＝ＢＤ
⌒
⌒
把圆沿着直径CD折叠时，CD两侧的两个半圆重合，　
点A与点B重合，AE与BE重合，ＡＣ　和　ＢＣ　
重合，ＡＤ和　ＢＤ重合．
⌒
⌒
⌒
⌒
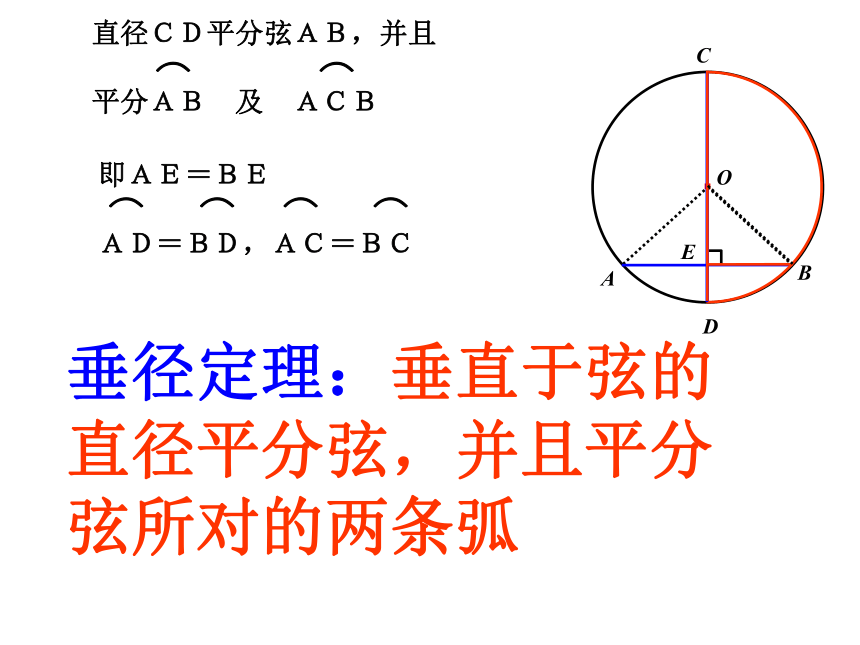
直径ＣＤ平分弦ＡＢ，并且
平分ＡＢ　及　ＡＣＢ
⌒
⌒
·
O
A
B
C
D
E
即ＡＥ＝ＢＥ　
ＡＤ＝ＢＤ，ＡＣ＝ＢＣ
⌒
⌒
⌒
⌒
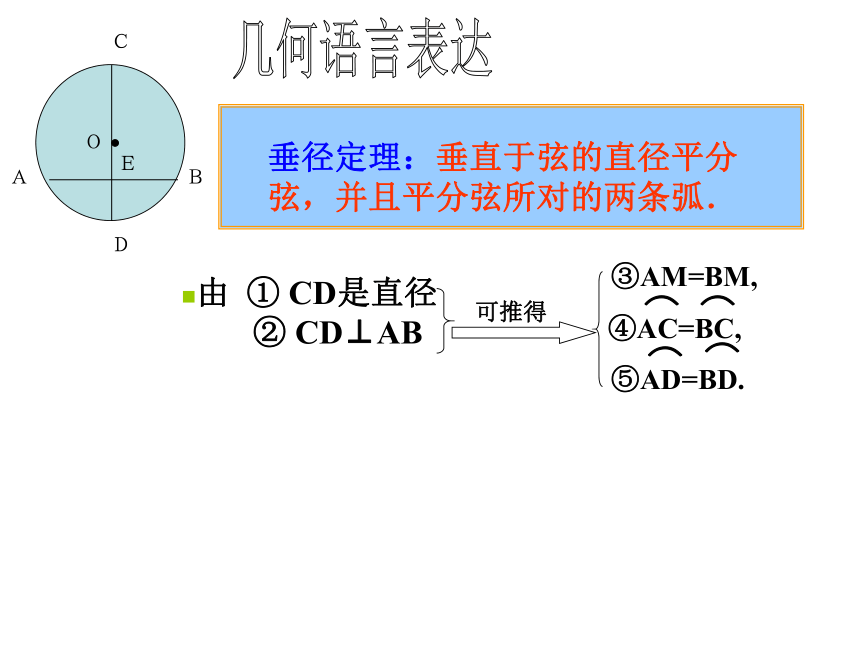
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧
③AM=BM,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
Ｄ
Ｃ
Ａ
Ｂ
Ｅ
Ｏ
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．
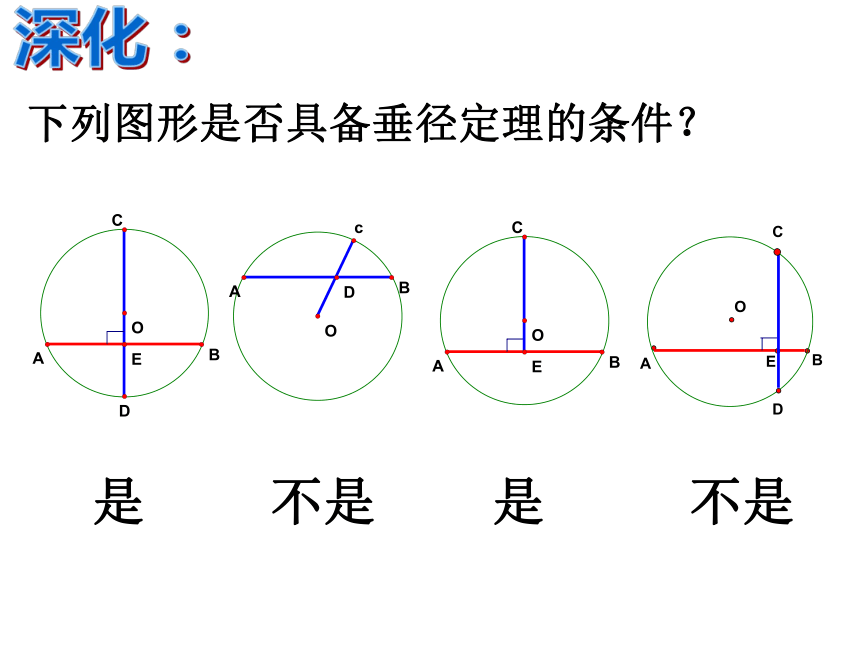
下列图形是否具备垂径定理的条件？
是
不是
是
不是
O
E
D
C
A
B
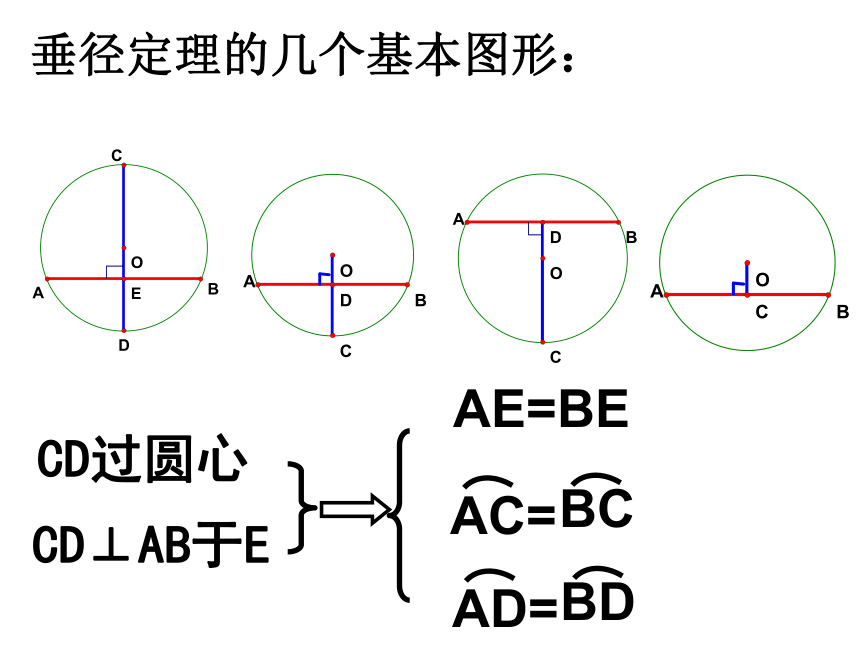
垂径定理的几个基本图形：
CD过圆心
CD⊥AB于E
AE=BE
AC=
BC
AD=
BD
思考：平分弦（不是直径）的直径有什么性质？
如图:
AB是⊙O的一条弦，直径CD交AB于M，AM=BM
垂径定理的推论
●O
A
B
C
D
M└
连接OA,OB,则OA=OB.
在△OAM和△OBM中,
∵OA=OB，OM=OM，AM=BM
∴△OAM≌△OBM.
∴∠AMO= ∠ BMO.
∴CD⊥AB
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
　AD =BD.
平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.
（1）
（4）
（5）
（2）
（3）
（1）
（5）
（2）
（3）
（4）
讨论
（1）
（3）
（2）
（4）
（5）
（1）
（4）
（2）
（3）
（5）
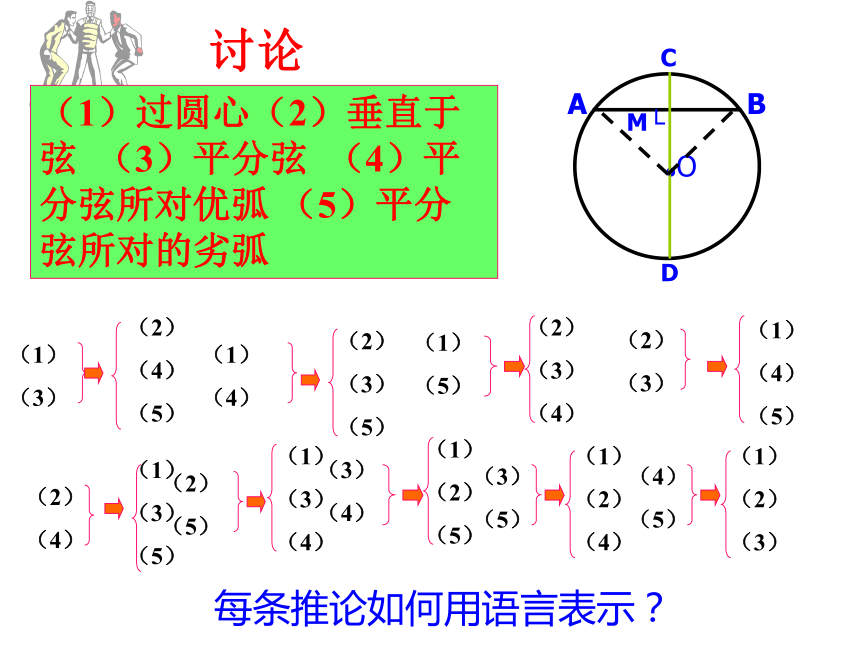
（1）过圆心（2）垂直于弦 （3）平分弦 （4）平分弦所对优弧 （5）平分弦所对的劣弧
（3）
（5）
（3）
（4）
（1）
（2）
（5）
（2）
（4）
（1）
（3）
（5）
（2）
（5）
（1）
（3）
（4）
（1）
（2）
（4）
（4）
（5）
（1）
（2）
（3）
●O
A
B
C
D
M└
每条推论如何用语言表示？
（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧
（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧
（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧
（4） …（5）… （6）…
（7）… （8）… （9）…
根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备
（1）过圆心 （2）垂直于弦 （3）平分弦
（4）平分弦所对的优弧 （5）平分弦所对的劣弧
上述五个条件中的任何两个条件都可以推出其他三个结论
结论
一、判断下列说法的正误
①平分弧的直径必平分弧所对的弦
　②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中，如果一条直线经过圆心且平分弦，　
　必平分此弦所对的弧
⑧分别过弦的三等分点作弦的垂线，将弦所对　
　的两条弧分别三等分
●O
A
B
C
D
M└
3．半径为2cm的圆中，过半径中点且
垂直于这条半径的弦长是 。
8cm
A
B
O
E
A
B
O
E
O
A
B
E
1．半径为4cm的⊙O中，弦AB=4cm,
那么圆心O到弦AB的距离是 。
2． ⊙O的直径为10cm，圆心O到弦AB的 距离为3cm，则弦AB的长是 。
二、填空：
●O
A
B
C
D
1.两条弦在圆心的同侧
●O
A
B
C
D
2.两条弦在圆心的两侧
4、⊙O的半径为10cm，弦AB∥CD，
AB=16，CD=12，则AB、CD间的
距离是___ .
2cm
或14cm
如图, △ABC的三个顶点在⊙O上，OE⊥AB于E，OF ⊥AC于F。
求证：EF∥BC，EF=
练习
O
A
B
C
E
F
∟
∟
∵OE⊥AB ∴E为AB的中点
∵OF ⊥AC ∴ F为AC的中点
∴EF为三角形ABC的中位线∴
1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．
·
O
A
B
E
再来！你行吗？
解：
答：⊙O的半径为5cm.
在Rt △ AOE 中
2：已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。
求证：AC＝BD。
证明：过O作OE⊥AB，垂足为E，
则AE＝BE，CE＝DE。
AE－CE＝BE－DE。
所以，AC＝BD
E
.
A
C
D
B
O
实际上，往往只需从圆心作一条与弦垂直的线段.就可以利用垂径定理来解决有关问题了.
3、已知：⊙O中弦AB∥CD。
求证：AC＝BD
⌒
⌒
证明：作直径MN⊥AB。
∵AB∥CD，∴MN⊥CD。
则AM＝BM，CM＝DM（垂直平分弦的直径平分弦所对的弦）
AM－CM＝BM－DM
∴AC＝BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
M
C
D
A
B
O
N
你能讲解吗？
夹在两条平行弦间的弧相等.
你能有一句话概括一下吗？
小结:
解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件。
.
C
D
A
B
O
M
N
E
.
A
C
D
B
O
.
A
B
O
说出你这节课的收获和体验，让大家与你一起分享！！！
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
垂径定理:
在解决有关圆的问题时，可以利用垂径定理将其转化为解直角三角形的问题 。
根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备
（1）过圆心 （2）垂直于弦 （3）平分弦
（4）平分弦所对的优弧 （5）平分弦所对的劣弧
上述五个条件中的任何两个条件都可以推出其他三个结论
垂径定理与推论的应用
如图，⊙O的直径为10，弦AB=8，P是弦AB上一个动点，
求OP的取值范围.
O
A
B
P
练习
3≤OP≤5
例1 如图，已知在⊙O中，弦AB的长为8厘米，圆心O到AB的距离为3厘米，求⊙O的半径.
解：连结OA。过O作OE⊥AB，垂足为E，则OE＝3厘米，AE＝BE。∵AB＝8厘米 ∴AE＝4厘米
在RtAOE中，根据勾股定理有OA＝5厘米 ∴⊙O的半径为5厘米。
.
A
E
B
O
讲解
例１、图示，在圆Ｏ中，弦ＡＢ的长为８厘米，圆心Ｏ到ＡＢ的距离为３厘米，求圆Ｏ的半径。
　　例１题图　　 　变式１题图　　 变式２题图
变式１：若以Ｏ为圆心，再画一个圆交ＡＤ与Ｂ、Ｃ两点，则ＡＢ与ＣＤ之间存在怎样的大小关系？
变式２：若以Ｏ为圆心，在变式１题图的基础上再画一个圆，则ＥＡ与ＢＦ，ＥＣ与ＤＦ之间存在怎样的大小关系？
变式３：在变式１题图的基础上，连结ＯＡ、ＯＢ，将大圆隐去，得到下图，设ＯＡ＝ＯＢ，试证明ＡＣ＝ＢＤ。
变式４：在变式１题图的基础上，将小圆隐去，得到下图，设ＯC＝ＯD，试证明ＡＣ＝ＢＤ。
　　变式３题图　　　　 变式４题图
学生练习
已知：AB是⊙O直径，CD
是弦，AE⊥CD，BF⊥CD
求证：EC＝DF
.
A
O
B
E
C
D
F
如图,A、B、C在圆上,且AB=AC=5厘米, BC=8厘米，求圆的半径。
试一试
B
C
A
O
D
2.已知，⊙O的直径AB和弦CD相交于点E，AE=6厘米，EB=2厘米，∠BED=30°，
求CD的长。
说明：
解决有关圆的问题，
常常需要添加辅助线，
针对各种具体情况，辅助线的添加有一定的规律，本例和上例中作“垂直于弦的直径”就是一个很好的例证。
练习
E
O
A
B
C
D
F
在直径是20cm的⊙O中，∠AOB的度数是60°, 那么弦AB的弦心距是　　　　　.
D
A
B
O
圆的圆心到圆上弦的距离叫做弦心距。
如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
D
·
O
A
B
C
E
证明：
∴四边形ADOE为矩形，
又　∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
问题 ：你知道赵州桥吗 它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶．它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？
赵州桥主桥拱的半径是多少？
解得：R≈27．9（m）
B
O
D
A
C
R
解决求赵州桥拱半径的问题
在Rt△OAD中，由勾股定理，得
即 R2=18.72+（R－7.2）2
∴赵州桥的主桥拱半径约为27.9m.
OA2=AD2+OD2
AB=37.4，CD=7.2，
OD=OC－CD=R－7.2
解：因为
如图，用 ＡＢ 表示主桥拱，设 ＡＢ所在圆的圆心为O，半径为R．经过圆心O 作弦AB 的垂线OC，D为垂足，OC与AB 相交于点D，根据前面的结论，D 是AB 的中点，C是ＡＢ 的中点，CD 就是拱高．
⌒
⌒
⌒
7.2
18.7
如图，弓形ABC中，弦AC的长为8厘米，弦的中点到劣弧中点间的长度是2厘米，
求圆的半径。
练习
A
B
C
D
O
x
4
2
x-2
A
B
O
E
D
油的最大深度ED=OD－OE=200(mm)
或者油的最大深度ED=OD + OE=450(mm).
(1)
在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm,求油的最大深度。
OE=125(mm)
(2)
B
A
O
E
D
解：
如图，某城市住宅社区，在相邻两楼之间修建一个上面是半圆，下面是矩形的仿古通道，其中半圆拱的圆心距地面2米，半径为1.3米，现有一辆高2.5米，宽2.3米的送家具的卡车，问这辆卡车能否通过通道，请说明理由。
解：如图，用半圆O表示通道上面的半圆，AB为直径，弦CD平行AB，过O作于E，连结OD，据垂径定理知：
某地有一座圆弧形拱桥圆心为Ｏ，桥下水面宽度为７、2 m ，过O 作OC ⊥ AB 于D， 交圆弧于C，CD=2、4m， 现有一艘宽3m，船舱顶部为方形并高出水面（AB）2m的货船要经过拱桥，此货船能否顺利通过这座拱桥？
C
N
M
A
E
H
F
B
D
O
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
在Rt△OAD中，由勾股定理，得
解得 R=3.9（m）.
在Rt△ONH中，由勾股定理，得
∴此货船能顺利通过这座拱桥.