人教版必修2第五章:曲线运动
文档属性
| 名称 | 人教版必修2第五章:曲线运动 |

|
|
| 格式 | zip | ||
| 文件大小 | 697.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-06-10 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第五章 曲线运动
知识要点
一、曲线运动
1、条件或原因:F与v夹角θ(0<θ<180°)
2、速度方向:切线方向,时刻变
3、运动性质:变速运动。速度方向时刻变。
4、分析方法:将曲化直,分解为两个方向讨论
(一般互相垂直)
二、运动的合成和分解:类似力
1、合运动和分运动:实际运动为合运动,例:
飞机起飞、船过河、飞机投弹
2、运动的独立性原理:各分运动互不影响
3、说明:
(1)合运动和分运动具有同时性
(2)两匀速时一定是直线;一匀速一匀变速时一定是曲线;两匀变速时可能是直线( a合与v合同向时)
三、平抛
1、定义:(1)只受重力;(2)V0水平
2、轨迹:抛物线
3、分解:水平方向匀速直线和竖直方向自由落体
4、运动规律:
(1)x=V0t,y=gt2/2,
tanα=y/x=gt/2V0;
(2)Vx=V0,Vy=gt,V=
tanθ= Vy/Vx =gt/V0=2tanα;
(3)a=g,匀变速曲线运动
5、说明:
(1)t由y决定;
(2)x由y、V0共同决定;
(3) △t等时,△v=g△t等;
(4)V反向延长过x/2处
x
y
小球的运动就可以看成是水平和竖直两个方向上运动的合成.t时间内小球合位移是多大
s
合位移的方向
水平方向:
vx=v0
竖直方向:
vy=gt
合速度:
方向:
tanβ=v0/gt =2 tanα
β
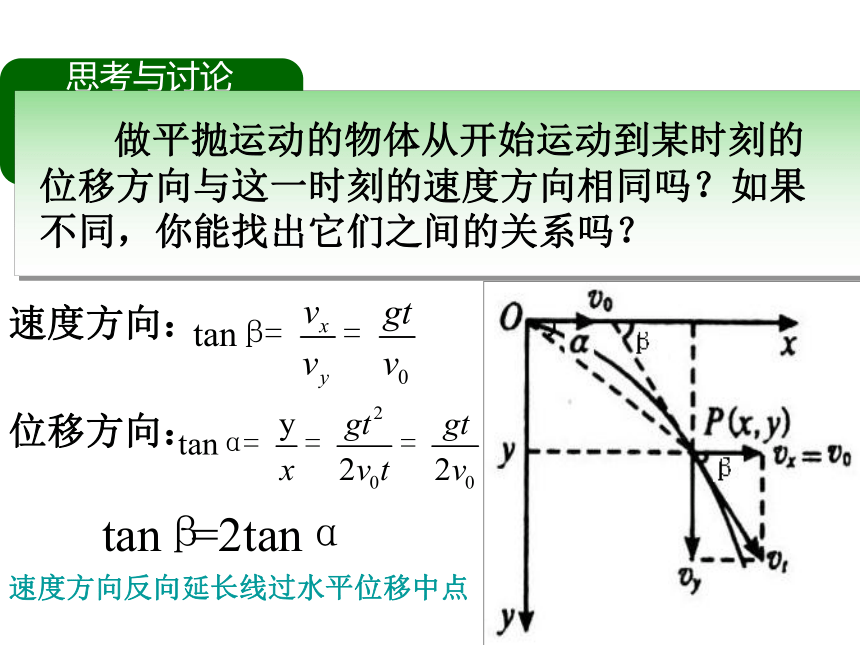
思考与讨论
做平抛运动的物体从开始运动到某时刻的位移方向与这一时刻的速度方向相同吗?如果不同,你能找出它们之间的关系吗?
速度方向:
位移方向:
速度方向反向延长线过水平位移中点
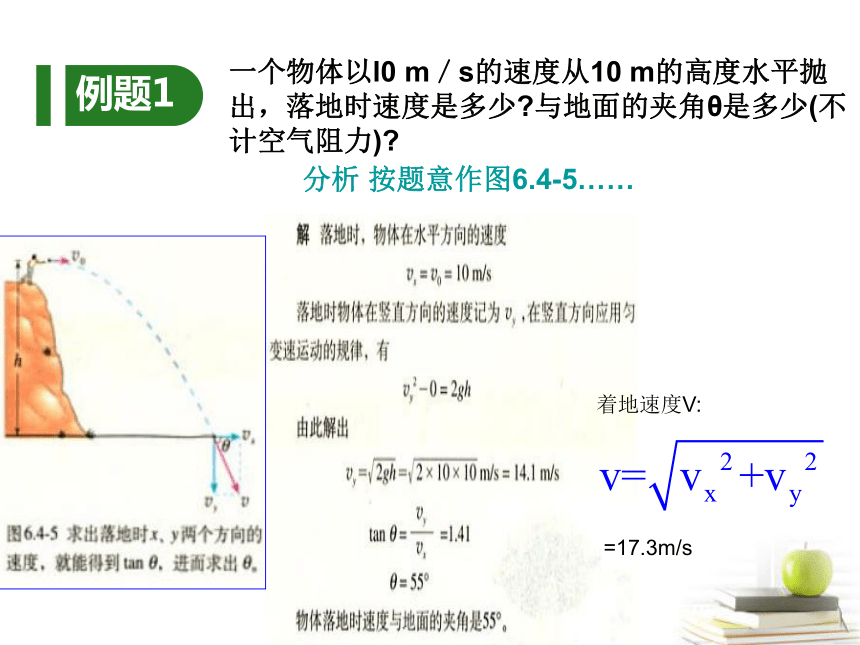
例题1
一个物体以l0 m/s的速度从10 m的高度水平抛出,落地时速度是多少 与地面的夹角θ是多少(不计空气阻力)
分析 按题意作图6.4-5……
着地速度V:
=17.3m/s
例题2
在例题1中如何计算物体在空中运动的时间?以及水平位移是多少?
解
小球在空中运动的时间:
竖直方向:
得:
=1.4s
可见时间是由高度决定的,与初速度无关
水平位移x=v0t=14m
可见水平位移是由初速度和高度共同决定的
四、匀速圆周运动
1、定义:相等时间内弧长相等,指速率等。
2、描述:V=s/t=2πr/T,当n用单位r/s 时, ω=θ/t=2π/Trad/s,n=f=1/T,V=ωr=2πfr
3、同一转动物体各点的ω、T、f、n同,
v不同(含大小),变的是矢量v、a向、F向
4、说明:同一转动物体各点的ω同;
两轮转动时 轮缘的点的V大小同
5、向心加速度:a=v2/r=ω2r=(4π2/T2)r=4π2f2r
6、向心力:F=ma=mv2/r=mω2r=m4π2f2r。
7、两种向心力:F供(F受) ≦>F向(需),离心,
r↓,继续匀速圆周,向心。
8、绳连物体过竖直最高点条件:V≥
v
FN
G
FN>G,即汽车对桥的压力大于其所受重力,处于超重状态。
2、汽车过凹桥时,在最低点时,车对凹桥的压力怎样?
例:过桥问题
1、汽车静止在桥上与通过桥时的状态是否相同?
FN
G
v
FN
v
G
FN
FN 3、汽车过凸桥时,在最高点时,车对凸桥的压力又怎样?
拱形桥
当汽车行驶速度越大,汽车对桥面的压力越小。当 时,压力FN为零。处于完全失重状态。
4、若汽车的运动速度变大,压力如何变化?
拱形桥
得 ,当 时
网兜系着盛有水的碗在竖直平面内做圆周运动,要过最高点,在最高点速度至少多大?
例:水流星
方程变成
实验
研究平抛物体的运动
1、用实验方法描出平抛物体的运动轨迹;
2、从实验轨迹求平抛物体的初速度.
实验目的
实验原理
1、平抛物体的运动的分解:
(1)水平方向的匀速直线运动;
(2)竖直方向的自由落体运动。
2、利用描迹法描出小球的运动轨迹,即小球作平抛运动的曲线,建立直角坐标系,测出曲线上的某一点的坐标(x,y),根据重力加速度g的数值,利用公式y=gt2/2和x=v0t,求出小球的水平速度v0,即为小球做平抛运动的初速度。
实验
实验仪器
平板、重垂线、铅笔、刻度尺、小球、弧形斜槽、白纸、有孔的硬纸片
实验
实验模拟
实验
实验步骤
1、安装调整斜槽,用图钉把白纸钉在竖直板上,在木板的左上角固定斜槽.
平衡法调整斜槽:将小球轻放在斜槽平直部分的末端处,若小球在平直轨道上的任意位置都静止,就表明水平已调好。
2、调整木板:用悬挂在槽口的重垂线把木板调整到竖直方向,并使木板平面与小球下落的竖直面平行。然后把重垂线方向记录到木板的白纸上,固定木板,使在重复实验的过程中,木板与斜槽的相对位置保持不变。
3、确定坐标O:把小球放在槽口处,用铅笔记下球在槽口时球心在图板上的水平投影点O,O点即为坐标原点。
实验
实验步骤
5、计算初速度:以O点为原点画出竖直向下的y轴和水平向右的x轴,并在曲线上选取ABCDEF六个不同的点,用刻度尺和三角板测出它们的坐标(x,y),用公式x=v0t,y=gt2/2,计算出小球的初速度v0,最后计算出v0的平均值,并将有关数据记入表格内。
4、描绘运动轨迹:在木板的平面上用手按住卡片,使卡片上有孔的一面保持水平,调整卡片的位置,使从槽上滚下的小球正好穿过卡片的孔,而不擦碰孔的边缘,然后用铅笔在卡片缺口上点个黑点,这就在白纸上记下了小球穿过孔时球心所对应的位置。保证小球每次从槽上开始滚下的位置都相同,用同样的方法,可找出小球平抛轨迹上的一系列位置。
取下白纸把这些位置连接成光滑的曲线即得小球平抛运动的轨迹。
实验
注意事项
1、实验中必须保证通过斜槽末端点的切线水平,方木板必须处在竖直面内且与小球运动轨迹所在的竖直平面平行,并使小球的运动靠近图板但不接触。
2、小球必须每次从同一位置滚下,即在斜槽上固定一个档板。
3、坐标原点(小球做平抛态度的起点)不是槽口的端点,应是小球在槽口时,球的球心在木板上的水平投影点。
4、要在斜轨上适当高度释放小球,使它以适当的水平初速度抛出,其轨道由图板左上角到达右上角,这样可以减小测量误差。
5、要在平抛轨道上选取距O点远些的点来计算球的初速度,这样可使结果的误差较小。
第五章 曲线运动
知识要点
一、曲线运动
1、条件或原因:F与v夹角θ(0<θ<180°)
2、速度方向:切线方向,时刻变
3、运动性质:变速运动。速度方向时刻变。
4、分析方法:将曲化直,分解为两个方向讨论
(一般互相垂直)
二、运动的合成和分解:类似力
1、合运动和分运动:实际运动为合运动,例:
飞机起飞、船过河、飞机投弹
2、运动的独立性原理:各分运动互不影响
3、说明:
(1)合运动和分运动具有同时性
(2)两匀速时一定是直线;一匀速一匀变速时一定是曲线;两匀变速时可能是直线( a合与v合同向时)
三、平抛
1、定义:(1)只受重力;(2)V0水平
2、轨迹:抛物线
3、分解:水平方向匀速直线和竖直方向自由落体
4、运动规律:
(1)x=V0t,y=gt2/2,
tanα=y/x=gt/2V0;
(2)Vx=V0,Vy=gt,V=
tanθ= Vy/Vx =gt/V0=2tanα;
(3)a=g,匀变速曲线运动
5、说明:
(1)t由y决定;
(2)x由y、V0共同决定;
(3) △t等时,△v=g△t等;
(4)V反向延长过x/2处
x
y
小球的运动就可以看成是水平和竖直两个方向上运动的合成.t时间内小球合位移是多大
s
合位移的方向
水平方向:
vx=v0
竖直方向:
vy=gt
合速度:
方向:
tanβ=v0/gt =2 tanα
β
思考与讨论
做平抛运动的物体从开始运动到某时刻的位移方向与这一时刻的速度方向相同吗?如果不同,你能找出它们之间的关系吗?
速度方向:
位移方向:
速度方向反向延长线过水平位移中点
例题1
一个物体以l0 m/s的速度从10 m的高度水平抛出,落地时速度是多少 与地面的夹角θ是多少(不计空气阻力)
分析 按题意作图6.4-5……
着地速度V:
=17.3m/s
例题2
在例题1中如何计算物体在空中运动的时间?以及水平位移是多少?
解
小球在空中运动的时间:
竖直方向:
得:
=1.4s
可见时间是由高度决定的,与初速度无关
水平位移x=v0t=14m
可见水平位移是由初速度和高度共同决定的
四、匀速圆周运动
1、定义:相等时间内弧长相等,指速率等。
2、描述:V=s/t=2πr/T,当n用单位r/s 时, ω=θ/t=2π/Trad/s,n=f=1/T,V=ωr=2πfr
3、同一转动物体各点的ω、T、f、n同,
v不同(含大小),变的是矢量v、a向、F向
4、说明:同一转动物体各点的ω同;
两轮转动时 轮缘的点的V大小同
5、向心加速度:a=v2/r=ω2r=(4π2/T2)r=4π2f2r
6、向心力:F=ma=mv2/r=mω2r=m4π2f2r。
7、两种向心力:F供(F受) ≦>F向(需),离心,
r↓,继续匀速圆周,向心。
8、绳连物体过竖直最高点条件:V≥
v
FN
G
FN>G,即汽车对桥的压力大于其所受重力,处于超重状态。
2、汽车过凹桥时,在最低点时,车对凹桥的压力怎样?
例:过桥问题
1、汽车静止在桥上与通过桥时的状态是否相同?
FN
G
v
FN
v
G
FN
FN
拱形桥
当汽车行驶速度越大,汽车对桥面的压力越小。当 时,压力FN为零。处于完全失重状态。
4、若汽车的运动速度变大,压力如何变化?
拱形桥
得 ,当 时
网兜系着盛有水的碗在竖直平面内做圆周运动,要过最高点,在最高点速度至少多大?
例:水流星
方程变成
实验
研究平抛物体的运动
1、用实验方法描出平抛物体的运动轨迹;
2、从实验轨迹求平抛物体的初速度.
实验目的
实验原理
1、平抛物体的运动的分解:
(1)水平方向的匀速直线运动;
(2)竖直方向的自由落体运动。
2、利用描迹法描出小球的运动轨迹,即小球作平抛运动的曲线,建立直角坐标系,测出曲线上的某一点的坐标(x,y),根据重力加速度g的数值,利用公式y=gt2/2和x=v0t,求出小球的水平速度v0,即为小球做平抛运动的初速度。
实验
实验仪器
平板、重垂线、铅笔、刻度尺、小球、弧形斜槽、白纸、有孔的硬纸片
实验
实验模拟
实验
实验步骤
1、安装调整斜槽,用图钉把白纸钉在竖直板上,在木板的左上角固定斜槽.
平衡法调整斜槽:将小球轻放在斜槽平直部分的末端处,若小球在平直轨道上的任意位置都静止,就表明水平已调好。
2、调整木板:用悬挂在槽口的重垂线把木板调整到竖直方向,并使木板平面与小球下落的竖直面平行。然后把重垂线方向记录到木板的白纸上,固定木板,使在重复实验的过程中,木板与斜槽的相对位置保持不变。
3、确定坐标O:把小球放在槽口处,用铅笔记下球在槽口时球心在图板上的水平投影点O,O点即为坐标原点。
实验
实验步骤
5、计算初速度:以O点为原点画出竖直向下的y轴和水平向右的x轴,并在曲线上选取ABCDEF六个不同的点,用刻度尺和三角板测出它们的坐标(x,y),用公式x=v0t,y=gt2/2,计算出小球的初速度v0,最后计算出v0的平均值,并将有关数据记入表格内。
4、描绘运动轨迹:在木板的平面上用手按住卡片,使卡片上有孔的一面保持水平,调整卡片的位置,使从槽上滚下的小球正好穿过卡片的孔,而不擦碰孔的边缘,然后用铅笔在卡片缺口上点个黑点,这就在白纸上记下了小球穿过孔时球心所对应的位置。保证小球每次从槽上开始滚下的位置都相同,用同样的方法,可找出小球平抛轨迹上的一系列位置。
取下白纸把这些位置连接成光滑的曲线即得小球平抛运动的轨迹。
实验
注意事项
1、实验中必须保证通过斜槽末端点的切线水平,方木板必须处在竖直面内且与小球运动轨迹所在的竖直平面平行,并使小球的运动靠近图板但不接触。
2、小球必须每次从同一位置滚下,即在斜槽上固定一个档板。
3、坐标原点(小球做平抛态度的起点)不是槽口的端点,应是小球在槽口时,球的球心在木板上的水平投影点。
4、要在斜轨上适当高度释放小球,使它以适当的水平初速度抛出,其轨道由图板左上角到达右上角,这样可以减小测量误差。
5、要在平抛轨道上选取距O点远些的点来计算球的初速度,这样可使结果的误差较小。
