7.3.2 正弦型函数的性质与图像-【新教材】人教B版(2019)高中数学必修第三册练习(Word版,含解析)
文档属性
| 名称 | 7.3.2 正弦型函数的性质与图像-【新教材】人教B版(2019)高中数学必修第三册练习(Word版,含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 90.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 07:31:53 | ||
图片预览




文档简介
7.3.2 正弦型函数的性质与图像
课后篇巩固提升
基础达标练
1.函数y=2sin的单调递增区间是( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
2.(多选)有下列四种变换方式,其中能将正弦曲线y=sin
x的图像变为y=sin2x+的图像的是( )
A.横坐标变为原来的,再向左平移个单位
B.横坐标变为原来的,再向左平移个单位
C.向左平移个单位,再将横坐标变为原来的
D.向左平移个单位,再将横坐标变为原来的
3.已知函数f(x)=Asin(2x+φ)A≠0,|φ|<,若x=是f(x)图像的一条对称轴方程,则下列说法正确的是( )
A.f(x)图像的一个对称中心为,0
B.f(x)在-上单调递减
C.f(x)的图像过点0,
D.f(x)的最大值是A
4.函数y=3-2sin2x-取得最大值时x的取值可能为( )
A.
B.
C.-
D.-
5.若函数y=5sin的周期不大于1,则自然数k的最小值为 .?
6.求函数f(x)=cos2x-sin
x,x∈的最大值.
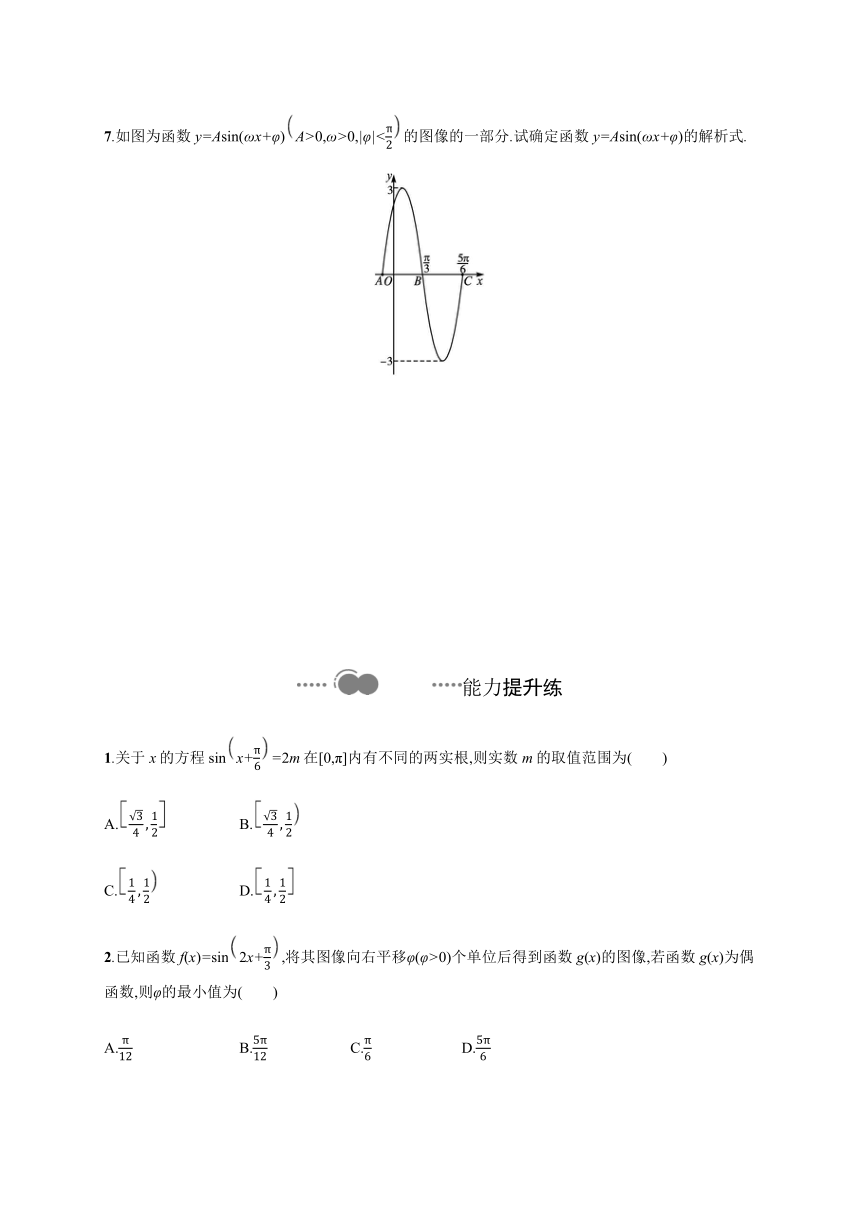
7.如图为函数y=Asin(ωx+φ)A>0,ω>0,|φ|<的图像的一部分.试确定函数y=Asin(ωx+φ)的解析式.
能力提升练
1.关于x的方程sinx+=2m在[0,π]内有不同的两实根,则实数m的取值范围为( )
A.
B.
C.
D.
2.已知函数f(x)=sin2x+,将其图像向右平移φ(φ>0)个单位后得到函数g(x)的图像,若函数g(x)为偶函数,则φ的最小值为( )
A.
B.
C.
D.
3.已知ω>0,函数f(x)=sin上单调递减,则ω的取值范围是 .?
4.函数y=Asin(ωx+φ)的最小值为-2,其图像相邻的最高点与最低点的横坐标之差是3π,又图像过点(0,1),则这个函数解析式是 ,单调递增区间为 .?
5.已知函数f(x)=Asinωx+(A>0,ω>0)的最小正周期为π,且该函数图像上的最低点的纵坐标为-3.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间及对称轴方程.
素养培优练
某景区每年都会接待大批游客,在景区的一家专门为游客提供食宿的客栈中,工作人员发现为游客准备的食物有些月份浪费严重.为了控制经营成本,减少浪费,计划适时调整投入.为此他们统计了每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数呈周期性变化,并且有以下规律:①每年相同的月份,入住客栈的游客人数基本相同;②入住客栈的游客人数在2月份最少,在8月份最多,相差约400;③2月份入住客栈的游客约有100人,随后逐月递增,在8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问客栈在哪几个月份要准备400份以上的食物?
7.3.2 正弦型函数的性质与图像
课后篇巩固提升
基础达标练
1.函数y=2sin的单调递增区间是( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
答案B
2.(多选)有下列四种变换方式,其中能将正弦曲线y=sin
x的图像变为y=sin2x+的图像的是( )
A.横坐标变为原来的,再向左平移个单位
B.横坐标变为原来的,再向左平移个单位
C.向左平移个单位,再将横坐标变为原来的
D.向左平移个单位,再将横坐标变为原来的
解析y=sin
x的图像横坐标变为原来的,再向左平移个单位,得y=sin2x+=sin2x+的图像,故A不正确;
y=sin
x的图像横坐标变为原来的,再向左平移个单位,得y=sin2x+=sin2x+的图像,故B正确;
y=sin
x的图像向左平移个单位,再将横坐标变为原来的,得y=sin2x+个单位,故C正确;
y=sin
x的图像向左平移个单位,再将横坐标变为原来的,得y=sin2x+的图像,故D不正确.
答案BC
3.已知函数f(x)=Asin(2x+φ)A≠0,|φ|<,若x=是f(x)图像的一条对称轴方程,则下列说法正确的是( )
A.f(x)图像的一个对称中心为,0
B.f(x)在-上单调递减
C.f(x)的图像过点0,
D.f(x)的最大值是A
解析∵x=是f(x)图像的一条对称轴方程,
∴2×+φ=+kπ(k∈Z),
又|φ|<,∴φ=,∴f(x)=Asin2x+.
f(x)图像的对称中心为,0(k∈Z),故A正确;由于A的正负未知,所以不能判断f(x)的单调性和最值,故B,D错误;f(0)=,故C错误.故选A.
答案A
4.函数y=3-2sin2x-取得最大值时x的取值可能为( )
A.
B.
C.-
D.-
解析当sin2x-=-1,
即2x-=-+2kπ,k∈Z时函数取得最大值,解得x=-+kπ,k∈Z,故当k=0时,x=-.故选C.
答案C
5.若函数y=5sin的周期不大于1,则自然数k的最小值为 .?
解析∵T=,且|T|≤1,即≤1.
又k为自然数,∴k≥6π,因此kmin=19.
答案19
6.求函数f(x)=cos2x-sin
x,x∈的最大值.
解由题得,f(x)=1-sin2x-sin
x=-sin
x+2+.
因为-≤x≤,所以当x=-,即sin
x=-时,f(x)取得最大值.
7.如图为函数y=Asin(ωx+φ)A>0,ω>0,|φ|<的图像的一部分.试确定函数y=Asin(ωx+φ)的解析式.
解(方法一)由图可知A=3,B,C,
则解得
故y=3sin.
(方法二)由振幅情况知A=3,,
T=π=,解得ω=2.
由B,则3sin=0,又|φ|<,故φ=.故y=3sin.
能力提升练
1.关于x的方程sinx+=2m在[0,π]内有不同的两实根,则实数m的取值范围为( )
A.
B.
C.
D.
解析由于0≤x≤π,所以≤x+,由于关于x的方程sinx+=2m在[0,π]内有不同的两实根,令u=x+,由函数y=sin
u与y=2m的图像可知,≤2m<1,解得≤m<.
答案C
2.已知函数f(x)=sin2x+,将其图像向右平移φ(φ>0)个单位后得到函数g(x)的图像,若函数g(x)为偶函数,则φ的最小值为( )
A.
B.
C.
D.
解析由题意得g(x)=sin2(x-φ)+=sin2x-2φ+(φ>0),因为g(x)为偶函数,所以函数g(x)的图像关于直线x=0对称,所以当x=0时,函数g(x)取得最大值或最小值,所以sin-2φ+=±1,所以-2φ+=kπ+,k∈Z,解得φ=-,k∈Z,因为φ>0,所以当k=-1时,φmin=,故选B.
答案B
3.已知ω>0,函数f(x)=sin上单调递减,则ω的取值范围是 .?
解析结合y=sin
ωx的图像可知y=sin
ωx在上单调递减,而y=sin=sin,可知y=sin
ωx的图像向左平移个单位之后可得y=sin的图像,故y=sin上单调递减,应有,解得≤ω≤.
答案
4.函数y=Asin(ωx+φ)的最小值为-2,其图像相邻的最高点与最低点的横坐标之差是3π,又图像过点(0,1),则这个函数解析式是 ,单调递增区间为 .?
答案y=2sin [6kπ-2π,6kπ+π],k∈Z
5.已知函数f(x)=Asinωx+(A>0,ω>0)的最小正周期为π,且该函数图像上的最低点的纵坐标为-3.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间及对称轴方程.
解(1)∵f(x)的最小正周期为π,
又ω>0,T==π,∴ω==2.
又函数f(x)图像上的最低点纵坐标为-3,且A>0,
∴A=3.∴f(x)=3sin2x+.
(2)由2kπ-≤2x+≤2kπ+,k∈Z,
可得kπ-≤x≤kπ+,k∈Z,
∴函数f(x)的单调递增区间为kπ-,kπ+,k∈Z,由2x++kπ,得x=,k∈Z,
∴函数f(x)的对称轴方程为x=,k∈Z.
素养培优练
某景区每年都会接待大批游客,在景区的一家专门为游客提供食宿的客栈中,工作人员发现为游客准备的食物有些月份浪费严重.为了控制经营成本,减少浪费,计划适时调整投入.为此他们统计了每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数呈周期性变化,并且有以下规律:①每年相同的月份,入住客栈的游客人数基本相同;②入住客栈的游客人数在2月份最少,在8月份最多,相差约400;③2月份入住客栈的游客约有100人,随后逐月递增,在8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问客栈在哪几个月份要准备400份以上的食物?
解(1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π),其中x=1,2,…,12.
根据①,可知这个函数的周期是12;
由②,可知f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200;
由③,可知f(x)在[2,8]上单调递增,且f(2)=100,
所以f(8)=500.
根据上述分析可得=12,故ω=.
又A=200,则B=500-200=300.
当x=2时,f(x)最小,当x=8时,f(x)最大,
故sin2×+φ=-1,且sin8×+φ=1.
又|φ|<π,故φ=-.
所以入住客栈的游客人数与月份之间的函数关系式为f(x)=200sinx-+300(x=1,2,…,12).
(2)由条件,可知200sinx-+300≥400,
化简得sinx-≥,即2kπ+x-≤2kπ+,k∈Z,解得12k+6≤x≤12k+10,k∈Z.
因为x∈N
,且1≤x≤12,故x=6,7,8,9,10.即客栈在6,7,8,9,10这五个月份要准备400份以上的食物.
课后篇巩固提升
基础达标练
1.函数y=2sin的单调递增区间是( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
2.(多选)有下列四种变换方式,其中能将正弦曲线y=sin
x的图像变为y=sin2x+的图像的是( )
A.横坐标变为原来的,再向左平移个单位
B.横坐标变为原来的,再向左平移个单位
C.向左平移个单位,再将横坐标变为原来的
D.向左平移个单位,再将横坐标变为原来的
3.已知函数f(x)=Asin(2x+φ)A≠0,|φ|<,若x=是f(x)图像的一条对称轴方程,则下列说法正确的是( )
A.f(x)图像的一个对称中心为,0
B.f(x)在-上单调递减
C.f(x)的图像过点0,
D.f(x)的最大值是A
4.函数y=3-2sin2x-取得最大值时x的取值可能为( )
A.
B.
C.-
D.-
5.若函数y=5sin的周期不大于1,则自然数k的最小值为 .?
6.求函数f(x)=cos2x-sin
x,x∈的最大值.
7.如图为函数y=Asin(ωx+φ)A>0,ω>0,|φ|<的图像的一部分.试确定函数y=Asin(ωx+φ)的解析式.
能力提升练
1.关于x的方程sinx+=2m在[0,π]内有不同的两实根,则实数m的取值范围为( )
A.
B.
C.
D.
2.已知函数f(x)=sin2x+,将其图像向右平移φ(φ>0)个单位后得到函数g(x)的图像,若函数g(x)为偶函数,则φ的最小值为( )
A.
B.
C.
D.
3.已知ω>0,函数f(x)=sin上单调递减,则ω的取值范围是 .?
4.函数y=Asin(ωx+φ)的最小值为-2,其图像相邻的最高点与最低点的横坐标之差是3π,又图像过点(0,1),则这个函数解析式是 ,单调递增区间为 .?
5.已知函数f(x)=Asinωx+(A>0,ω>0)的最小正周期为π,且该函数图像上的最低点的纵坐标为-3.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间及对称轴方程.
素养培优练
某景区每年都会接待大批游客,在景区的一家专门为游客提供食宿的客栈中,工作人员发现为游客准备的食物有些月份浪费严重.为了控制经营成本,减少浪费,计划适时调整投入.为此他们统计了每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数呈周期性变化,并且有以下规律:①每年相同的月份,入住客栈的游客人数基本相同;②入住客栈的游客人数在2月份最少,在8月份最多,相差约400;③2月份入住客栈的游客约有100人,随后逐月递增,在8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问客栈在哪几个月份要准备400份以上的食物?
7.3.2 正弦型函数的性质与图像
课后篇巩固提升
基础达标练
1.函数y=2sin的单调递增区间是( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
答案B
2.(多选)有下列四种变换方式,其中能将正弦曲线y=sin
x的图像变为y=sin2x+的图像的是( )
A.横坐标变为原来的,再向左平移个单位
B.横坐标变为原来的,再向左平移个单位
C.向左平移个单位,再将横坐标变为原来的
D.向左平移个单位,再将横坐标变为原来的
解析y=sin
x的图像横坐标变为原来的,再向左平移个单位,得y=sin2x+=sin2x+的图像,故A不正确;
y=sin
x的图像横坐标变为原来的,再向左平移个单位,得y=sin2x+=sin2x+的图像,故B正确;
y=sin
x的图像向左平移个单位,再将横坐标变为原来的,得y=sin2x+个单位,故C正确;
y=sin
x的图像向左平移个单位,再将横坐标变为原来的,得y=sin2x+的图像,故D不正确.
答案BC
3.已知函数f(x)=Asin(2x+φ)A≠0,|φ|<,若x=是f(x)图像的一条对称轴方程,则下列说法正确的是( )
A.f(x)图像的一个对称中心为,0
B.f(x)在-上单调递减
C.f(x)的图像过点0,
D.f(x)的最大值是A
解析∵x=是f(x)图像的一条对称轴方程,
∴2×+φ=+kπ(k∈Z),
又|φ|<,∴φ=,∴f(x)=Asin2x+.
f(x)图像的对称中心为,0(k∈Z),故A正确;由于A的正负未知,所以不能判断f(x)的单调性和最值,故B,D错误;f(0)=,故C错误.故选A.
答案A
4.函数y=3-2sin2x-取得最大值时x的取值可能为( )
A.
B.
C.-
D.-
解析当sin2x-=-1,
即2x-=-+2kπ,k∈Z时函数取得最大值,解得x=-+kπ,k∈Z,故当k=0时,x=-.故选C.
答案C
5.若函数y=5sin的周期不大于1,则自然数k的最小值为 .?
解析∵T=,且|T|≤1,即≤1.
又k为自然数,∴k≥6π,因此kmin=19.
答案19
6.求函数f(x)=cos2x-sin
x,x∈的最大值.
解由题得,f(x)=1-sin2x-sin
x=-sin
x+2+.
因为-≤x≤,所以当x=-,即sin
x=-时,f(x)取得最大值.
7.如图为函数y=Asin(ωx+φ)A>0,ω>0,|φ|<的图像的一部分.试确定函数y=Asin(ωx+φ)的解析式.
解(方法一)由图可知A=3,B,C,
则解得
故y=3sin.
(方法二)由振幅情况知A=3,,
T=π=,解得ω=2.
由B,则3sin=0,又|φ|<,故φ=.故y=3sin.
能力提升练
1.关于x的方程sinx+=2m在[0,π]内有不同的两实根,则实数m的取值范围为( )
A.
B.
C.
D.
解析由于0≤x≤π,所以≤x+,由于关于x的方程sinx+=2m在[0,π]内有不同的两实根,令u=x+,由函数y=sin
u与y=2m的图像可知,≤2m<1,解得≤m<.
答案C
2.已知函数f(x)=sin2x+,将其图像向右平移φ(φ>0)个单位后得到函数g(x)的图像,若函数g(x)为偶函数,则φ的最小值为( )
A.
B.
C.
D.
解析由题意得g(x)=sin2(x-φ)+=sin2x-2φ+(φ>0),因为g(x)为偶函数,所以函数g(x)的图像关于直线x=0对称,所以当x=0时,函数g(x)取得最大值或最小值,所以sin-2φ+=±1,所以-2φ+=kπ+,k∈Z,解得φ=-,k∈Z,因为φ>0,所以当k=-1时,φmin=,故选B.
答案B
3.已知ω>0,函数f(x)=sin上单调递减,则ω的取值范围是 .?
解析结合y=sin
ωx的图像可知y=sin
ωx在上单调递减,而y=sin=sin,可知y=sin
ωx的图像向左平移个单位之后可得y=sin的图像,故y=sin上单调递减,应有,解得≤ω≤.
答案
4.函数y=Asin(ωx+φ)的最小值为-2,其图像相邻的最高点与最低点的横坐标之差是3π,又图像过点(0,1),则这个函数解析式是 ,单调递增区间为 .?
答案y=2sin [6kπ-2π,6kπ+π],k∈Z
5.已知函数f(x)=Asinωx+(A>0,ω>0)的最小正周期为π,且该函数图像上的最低点的纵坐标为-3.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间及对称轴方程.
解(1)∵f(x)的最小正周期为π,
又ω>0,T==π,∴ω==2.
又函数f(x)图像上的最低点纵坐标为-3,且A>0,
∴A=3.∴f(x)=3sin2x+.
(2)由2kπ-≤2x+≤2kπ+,k∈Z,
可得kπ-≤x≤kπ+,k∈Z,
∴函数f(x)的单调递增区间为kπ-,kπ+,k∈Z,由2x++kπ,得x=,k∈Z,
∴函数f(x)的对称轴方程为x=,k∈Z.
素养培优练
某景区每年都会接待大批游客,在景区的一家专门为游客提供食宿的客栈中,工作人员发现为游客准备的食物有些月份浪费严重.为了控制经营成本,减少浪费,计划适时调整投入.为此他们统计了每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数呈周期性变化,并且有以下规律:①每年相同的月份,入住客栈的游客人数基本相同;②入住客栈的游客人数在2月份最少,在8月份最多,相差约400;③2月份入住客栈的游客约有100人,随后逐月递增,在8月份达到最多.
(1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系;
(2)请问客栈在哪几个月份要准备400份以上的食物?
解(1)设该函数为f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π),其中x=1,2,…,12.
根据①,可知这个函数的周期是12;
由②,可知f(2)最小,f(8)最大,且f(8)-f(2)=400,故该函数的振幅为200;
由③,可知f(x)在[2,8]上单调递增,且f(2)=100,
所以f(8)=500.
根据上述分析可得=12,故ω=.
又A=200,则B=500-200=300.
当x=2时,f(x)最小,当x=8时,f(x)最大,
故sin2×+φ=-1,且sin8×+φ=1.
又|φ|<π,故φ=-.
所以入住客栈的游客人数与月份之间的函数关系式为f(x)=200sinx-+300(x=1,2,…,12).
(2)由条件,可知200sinx-+300≥400,
化简得sinx-≥,即2kπ+x-≤2kπ+,k∈Z,解得12k+6≤x≤12k+10,k∈Z.
因为x∈N
,且1≤x≤12,故x=6,7,8,9,10.即客栈在6,7,8,9,10这五个月份要准备400份以上的食物.
