八年级数学下册第十九章第一节平行四边形的定义及性质
文档属性
| 名称 | 八年级数学下册第十九章第一节平行四边形的定义及性质 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-11 11:12:02 | ||
图片预览





文档简介
(共36张PPT)
§19.1 .1平行四边形的定义、性质(1)
平行四边形
北京市剑桥中学 姬红喜
1、理解什么是平行四边形及其表示方法;
2、探索平行四边形的性质;
3、能利用平行四边形的性质解决问题。
学习目标:
学习重点:
平行四边形的性质探究.
学习难点:
应用平行四边形的性质解决问题。
2、 平行线的判定方法有哪些?
1、平行线有哪些性质?
知识回忆
(1)两直线平行,同位角相等、内错角相等、同旁内角互补。
(2)平行于同一条直线的两条直线平行。
(3)垂直于同一条直线的两条直线平行。
(2)同位角相等,两直线平行。
(3)内错角相等,两直线平行。
(4)同旁内角互补,两直线平行。
(5)平行于同一条直线的两条直线平行。
(6)垂直于同一条直线的两条直线平行。
(1)根据定义:在同一平面内,不相交的两条直线是平行线(不常用)
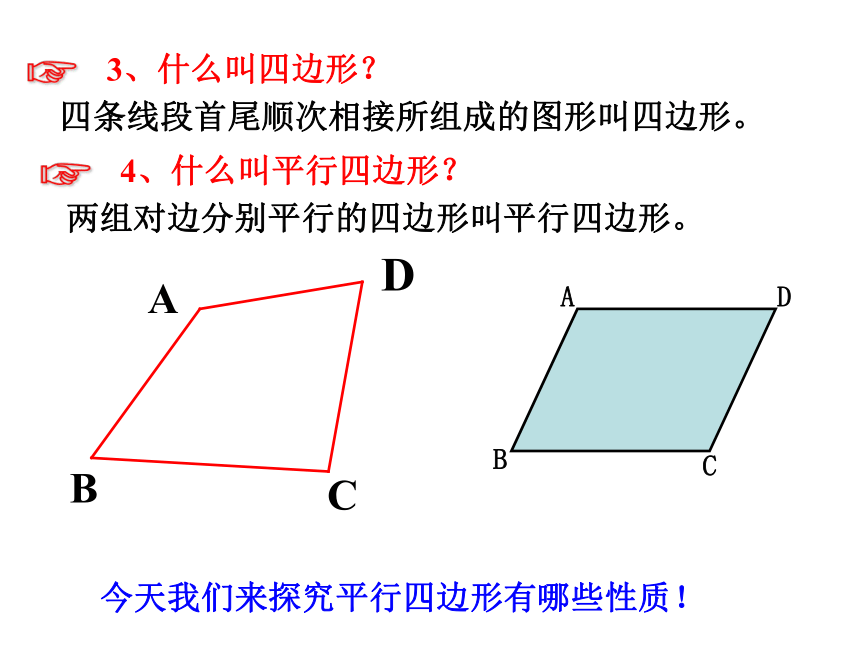
四条线段首尾顺次相接所组成的图形叫四边形。
3、什么叫四边形?
D
C
A
B
4、什么叫平行四边形?
两组对边分别平行的四边形叫平行四边形。
A
B
C
D
今天我们来探究平行四边形有哪些性质!
自学提纲
自学课本P83,讨论解决以下问题:
1、什么是平行四边形?如何表示一个平行四边形?用几何语言描述平行四边形;
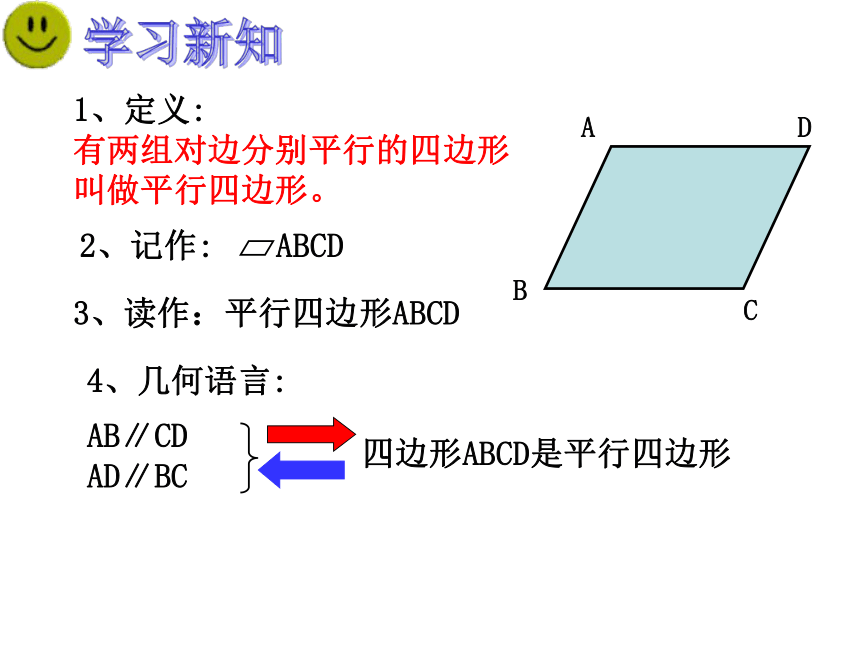
1、定义:
有两组对边分别平行的四边形 叫做平行四边形。
2、记作:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
四边形ABCD是平行四边形
AB∥CD AD∥BC
A
B
C
D
A
B
C
D
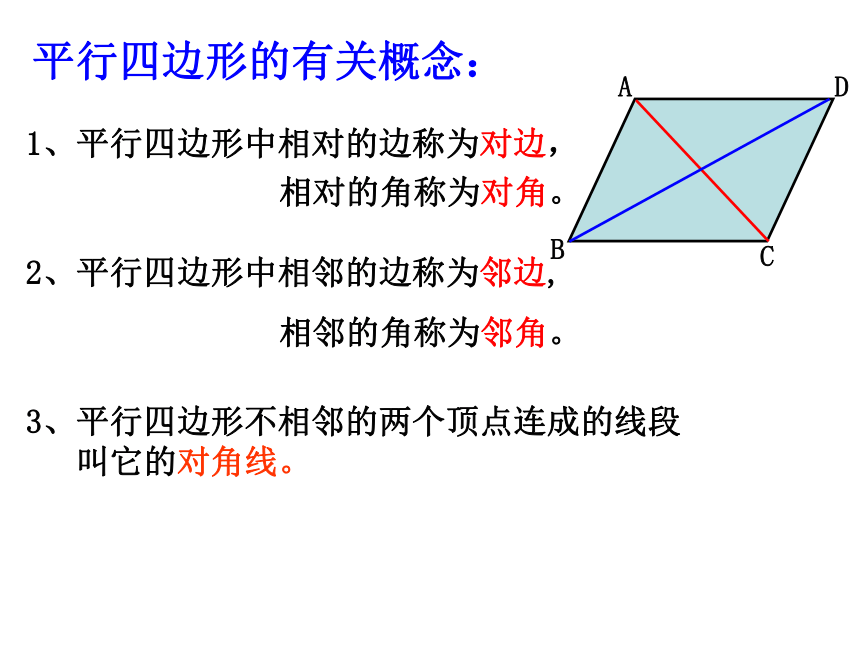
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线。
自学提纲
自学课本P83-85,讨论解决以下问题:
1、什么是平行四边形?如何表示一个平行四边形?用几何语言描述平行四边形;
2、平行四边形有哪些性质?为什么?
3、小组合作:看懂P84例1和 P85例2
●
A
D
O
C
B
D
B
O
C
A
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是中心对称图形,点O叫对称中心。
一个图形绕一个点O旋转180°后与自身重合,这时我们说这个图形是中心对称图形,点O叫对称中心。
O
A
B
C
D
(C)
(A)
(B)
(D)
AD=BC AB=CD
∠BAD=∠DCB
∠ABC=∠CDA
思考:平行四边形的邻角有什么关系呢?
对边相等
对角相等
对角线互相平分
邻角互补
发现了什么?
●
O
A
D
C
B
已知: ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连接AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 △ABC和△CDA中
A
B
C
D
1
2
3
4
猜想:平行四边形的对边相等、对角相等。如何证明?
已知: ABCD中(如图)对角线
AC、BD相交于点O。
求证:OA=OC,OB=OD
证明:
∵AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
又∵ AD=BC,
∴ △AOD≌△BOC(ASA)
(平行四边形的对边相等)
∴OA=OC,OB=OD
A
B
C
D
1
2
3
4
猜想:平行四边形的对角线互相平分。如何证明?
O
即平行四边形对角线互相平分
平行四边形的性质1:
平行四边形的对边平行且相等;
平行四边形的对角相等;邻角互补。
平行四边形的性质2:
∵四边形ABCD是平行四边形
∴AB∥CD AD∥BC
∵四边形ABCD是平行四边形
∴∠A=∠C ∠B=∠D
∠A+∠B=180°∠B+∠C=180°…
平行四边形的对角线互相平分
平行四边形的性质3:
AC=BD吗?
O
D
C
B
A
如图,∵ ABCD
符号语言:
∴
1、已知一个平行四边形的两个内角之比为
1︰2,你能求出平行四边形每个内角的度数吗
A
B
C
D
解:∵四边形ABCD是平行四边形
∴∠A+∠B=180° ∠A=∠C ∠B=∠D
又∵∠A :∠B=1:2
∴∠B= 2∠A
∴∠A+2∠A=180°
∴∠A=60°
∴∠B=120°
∴∠C=∠A=60° ∠D=∠B=60°
2、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
四边形ABCD是平行四边形
3、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长及 ABCD 的面积.
B
D
C
A
O
8
10
解:∵四边形ABCD是平行四边形
∴BC=AD=8 CD=AD=10
又∵AC⊥BC
∴⊿ABC是直角三角形
又∵OA=OC
4、已知如图,在 ABCD中, E、F分别是边BC和AD上的点,且BE=DF。求证:①△ABE≌△CDF
②AE=CF
A
B
C
D
E
F
解:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠B=∠D
∵BE=DF
∴ △ABE≌△CDF(SAS)
∴AE=CF
(全等三角形的对应边相等)
选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm
3、 ABCD中, ∠ A=43 ° ,过点A作BC和CD的垂线,那么这两条垂线的夹角度数为 ( )
A、113° B、115 ° C、137° D、90°
C
A
C
4、已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DF
A
B
C
D
O
E
F
证明:∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )
两直线平行,内错角相等
平行四边形的对角线互相平分
SAS
全等三角形的对应边相等
5、已知 ABCD中,AE⊥BD, AF⊥BD,垂足为E、F,
求证:EB=DF
A
B
C
D
E
F
证明:∵AE⊥BD,CF ⊥ BD
∴∠AEB=90°,∠CFD=90°
∴∠ AEB=∠CFD
又四边形ABCD是平行四边形
∴ AB=CD,∠ABE=∠CDF
∴ ⊿ABE≌⊿CDF
∴ BE=DF
ABCD中,∠A=150°,AB=8cm,BC=10cm,
求:四边形ABCD的面积
A
B
C
D
E
解:过点A作AE ⊥ BC交BC于E。
∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠BAD+∠B=180°
∵ ∠BAD=150 ° ∴∠B=30 °
在Rt⊿ABE中,∠B=30 °
∴AE= AB=4, ∴ S ABCD=4×10=40(cm)
如图,在 ABCD中,AC=4 ㎝ ,CD=3 ㎝ ,BC=5 ㎝ ,则 ABCD的面积
为 ________ .
A
D
C
B
4
5
3
12㎝2
如图,在 ABCD中,BE平分∠ABC交AD于E,BC=8㎝,CD=6㎝, ∠D=60°,则下列说法中错误的是( )
∠C=120° B. AE=6 ㎝
C. AD=8 ㎝ D. ∠BED=140 °
A
B
C
D
E
D
6
8
60°
6
6
小组抢答!
取出两张全等的三角形纸片拼平行四边形,你能拼出几种不同的平行四边形
平行四边形相对的两边有怎样的位置关系?
本课小结
A
D
B
C
定 义
表示方法
性 质
两组对边分别平行的四边形叫做 平 行 四边形。其不
相邻的两个顶点连成的线段叫它的对角线。
平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。
1、边:对边平行且相等;
2、角:对角相等, 邻角互补;
3、对角线:对角线互相平分;
4、对称性:是中心对称图形,对称中心
是对角线的交点。
作 业
1、2
P86练习题
19
四边形
1、2、
P84练习题
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
-------毕达哥拉斯
已知平面上任意三点A、B、C,是否存在一点D,使A、B、C、D四点围成一个平行四边形。若存在,请你作出图形;若不存在,请说明理由。
1、在本子上画一个平行四边形,并把它表示出来。
2、画出平行四边形的两条对角线。
3、用一张半透明的纸复制你刚才画的平行四边形,并将复制后的平行四边形绕对角线的交点旋转180度,你有什么发现?
§19.1 .1平行四边形的定义、性质(1)
平行四边形
北京市剑桥中学 姬红喜
1、理解什么是平行四边形及其表示方法;
2、探索平行四边形的性质;
3、能利用平行四边形的性质解决问题。
学习目标:
学习重点:
平行四边形的性质探究.
学习难点:
应用平行四边形的性质解决问题。
2、 平行线的判定方法有哪些?
1、平行线有哪些性质?
知识回忆
(1)两直线平行,同位角相等、内错角相等、同旁内角互补。
(2)平行于同一条直线的两条直线平行。
(3)垂直于同一条直线的两条直线平行。
(2)同位角相等,两直线平行。
(3)内错角相等,两直线平行。
(4)同旁内角互补,两直线平行。
(5)平行于同一条直线的两条直线平行。
(6)垂直于同一条直线的两条直线平行。
(1)根据定义:在同一平面内,不相交的两条直线是平行线(不常用)
四条线段首尾顺次相接所组成的图形叫四边形。
3、什么叫四边形?
D
C
A
B
4、什么叫平行四边形?
两组对边分别平行的四边形叫平行四边形。
A
B
C
D
今天我们来探究平行四边形有哪些性质!
自学提纲
自学课本P83,讨论解决以下问题:
1、什么是平行四边形?如何表示一个平行四边形?用几何语言描述平行四边形;
1、定义:
有两组对边分别平行的四边形 叫做平行四边形。
2、记作:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
四边形ABCD是平行四边形
AB∥CD AD∥BC
A
B
C
D
A
B
C
D
1、平行四边形中相对的边称为对边,
相对的角称为对角。
2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。
平行四边形的有关概念:
3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线。
自学提纲
自学课本P83-85,讨论解决以下问题:
1、什么是平行四边形?如何表示一个平行四边形?用几何语言描述平行四边形;
2、平行四边形有哪些性质?为什么?
3、小组合作:看懂P84例1和 P85例2
●
A
D
O
C
B
D
B
O
C
A
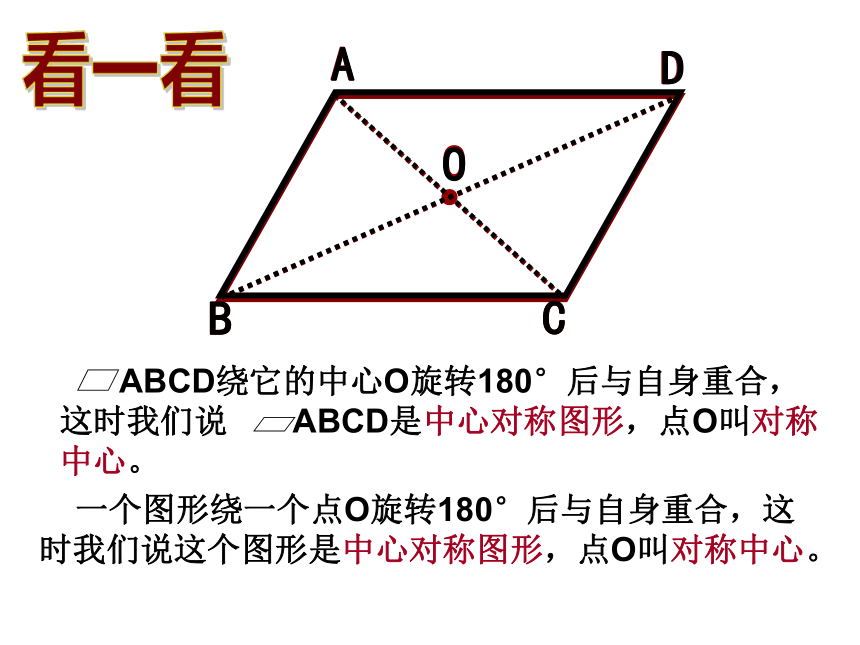
ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是中心对称图形,点O叫对称中心。
一个图形绕一个点O旋转180°后与自身重合,这时我们说这个图形是中心对称图形,点O叫对称中心。
O
A
B
C
D
(C)
(A)
(B)
(D)
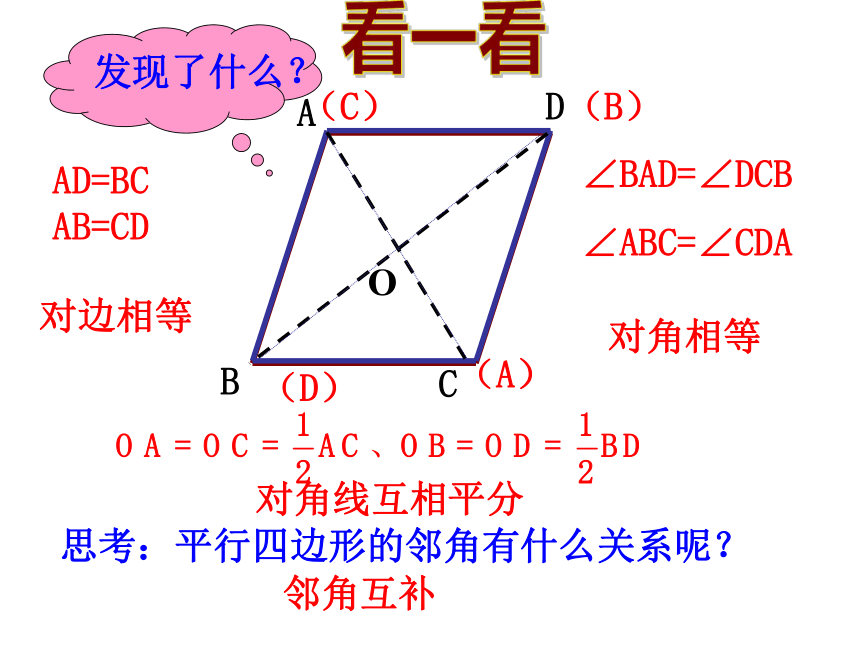
AD=BC AB=CD
∠BAD=∠DCB
∠ABC=∠CDA
思考:平行四边形的邻角有什么关系呢?
对边相等
对角相等
对角线互相平分
邻角互补
发现了什么?
●
O
A
D
C
B
已知: ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连接AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在 △ABC和△CDA中
A
B
C
D
1
2
3
4
猜想:平行四边形的对边相等、对角相等。如何证明?
已知: ABCD中(如图)对角线
AC、BD相交于点O。
求证:OA=OC,OB=OD
证明:
∵AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
又∵ AD=BC,
∴ △AOD≌△BOC(ASA)
(平行四边形的对边相等)
∴OA=OC,OB=OD
A
B
C
D
1
2
3
4
猜想:平行四边形的对角线互相平分。如何证明?
O
即平行四边形对角线互相平分
平行四边形的性质1:
平行四边形的对边平行且相等;
平行四边形的对角相等;邻角互补。
平行四边形的性质2:
∵四边形ABCD是平行四边形
∴AB∥CD AD∥BC
∵四边形ABCD是平行四边形
∴∠A=∠C ∠B=∠D
∠A+∠B=180°∠B+∠C=180°…
平行四边形的对角线互相平分
平行四边形的性质3:
AC=BD吗?
O
D
C
B
A
如图,∵ ABCD
符号语言:
∴
1、已知一个平行四边形的两个内角之比为
1︰2,你能求出平行四边形每个内角的度数吗
A
B
C
D
解:∵四边形ABCD是平行四边形
∴∠A+∠B=180° ∠A=∠C ∠B=∠D
又∵∠A :∠B=1:2
∴∠B= 2∠A
∴∠A+2∠A=180°
∴∠A=60°
∴∠B=120°
∴∠C=∠A=60° ∠D=∠B=60°
2、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
四边形ABCD是平行四边形
3、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长及 ABCD 的面积.
B
D
C
A
O
8
10
解:∵四边形ABCD是平行四边形
∴BC=AD=8 CD=AD=10
又∵AC⊥BC
∴⊿ABC是直角三角形
又∵OA=OC
4、已知如图,在 ABCD中, E、F分别是边BC和AD上的点,且BE=DF。求证:①△ABE≌△CDF
②AE=CF
A
B
C
D
E
F
解:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,∠B=∠D
∵BE=DF
∴ △ABE≌△CDF(SAS)
∴AE=CF
(全等三角形的对应边相等)
选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm
3、 ABCD中, ∠ A=43 ° ,过点A作BC和CD的垂线,那么这两条垂线的夹角度数为 ( )
A、113° B、115 ° C、137° D、90°
C
A
C
4、已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DF
A
B
C
D
O
E
F
证明:∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )
两直线平行,内错角相等
平行四边形的对角线互相平分
SAS
全等三角形的对应边相等
5、已知 ABCD中,AE⊥BD, AF⊥BD,垂足为E、F,
求证:EB=DF
A
B
C
D
E
F
证明:∵AE⊥BD,CF ⊥ BD
∴∠AEB=90°,∠CFD=90°
∴∠ AEB=∠CFD
又四边形ABCD是平行四边形
∴ AB=CD,∠ABE=∠CDF
∴ ⊿ABE≌⊿CDF
∴ BE=DF
ABCD中,∠A=150°,AB=8cm,BC=10cm,
求:四边形ABCD的面积
A
B
C
D
E
解:过点A作AE ⊥ BC交BC于E。
∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠BAD+∠B=180°
∵ ∠BAD=150 ° ∴∠B=30 °
在Rt⊿ABE中,∠B=30 °
∴AE= AB=4, ∴ S ABCD=4×10=40(cm)
如图,在 ABCD中,AC=4 ㎝ ,CD=3 ㎝ ,BC=5 ㎝ ,则 ABCD的面积
为 ________ .
A
D
C
B
4
5
3
12㎝2
如图,在 ABCD中,BE平分∠ABC交AD于E,BC=8㎝,CD=6㎝, ∠D=60°,则下列说法中错误的是( )
∠C=120° B. AE=6 ㎝
C. AD=8 ㎝ D. ∠BED=140 °
A
B
C
D
E
D
6
8
60°
6
6
小组抢答!
取出两张全等的三角形纸片拼平行四边形,你能拼出几种不同的平行四边形
平行四边形相对的两边有怎样的位置关系?
本课小结
A
D
B
C
定 义
表示方法
性 质
两组对边分别平行的四边形叫做 平 行 四边形。其不
相邻的两个顶点连成的线段叫它的对角线。
平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。
1、边:对边平行且相等;
2、角:对角相等, 邻角互补;
3、对角线:对角线互相平分;
4、对称性:是中心对称图形,对称中心
是对角线的交点。
作 业
1、2
P86练习题
19
四边形
1、2、
P84练习题
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
-------毕达哥拉斯
已知平面上任意三点A、B、C,是否存在一点D,使A、B、C、D四点围成一个平行四边形。若存在,请你作出图形;若不存在,请说明理由。
1、在本子上画一个平行四边形,并把它表示出来。
2、画出平行四边形的两条对角线。
3、用一张半透明的纸复制你刚才画的平行四边形,并将复制后的平行四边形绕对角线的交点旋转180度,你有什么发现?
