2021-2022学年人教版八年级数学上册《12.2 三角形全等的判定》同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册《12.2 三角形全等的判定》同步练习(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 308.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 00:00:00 | ||
图片预览

文档简介
12.2
三角形全等的判定
一.选择题
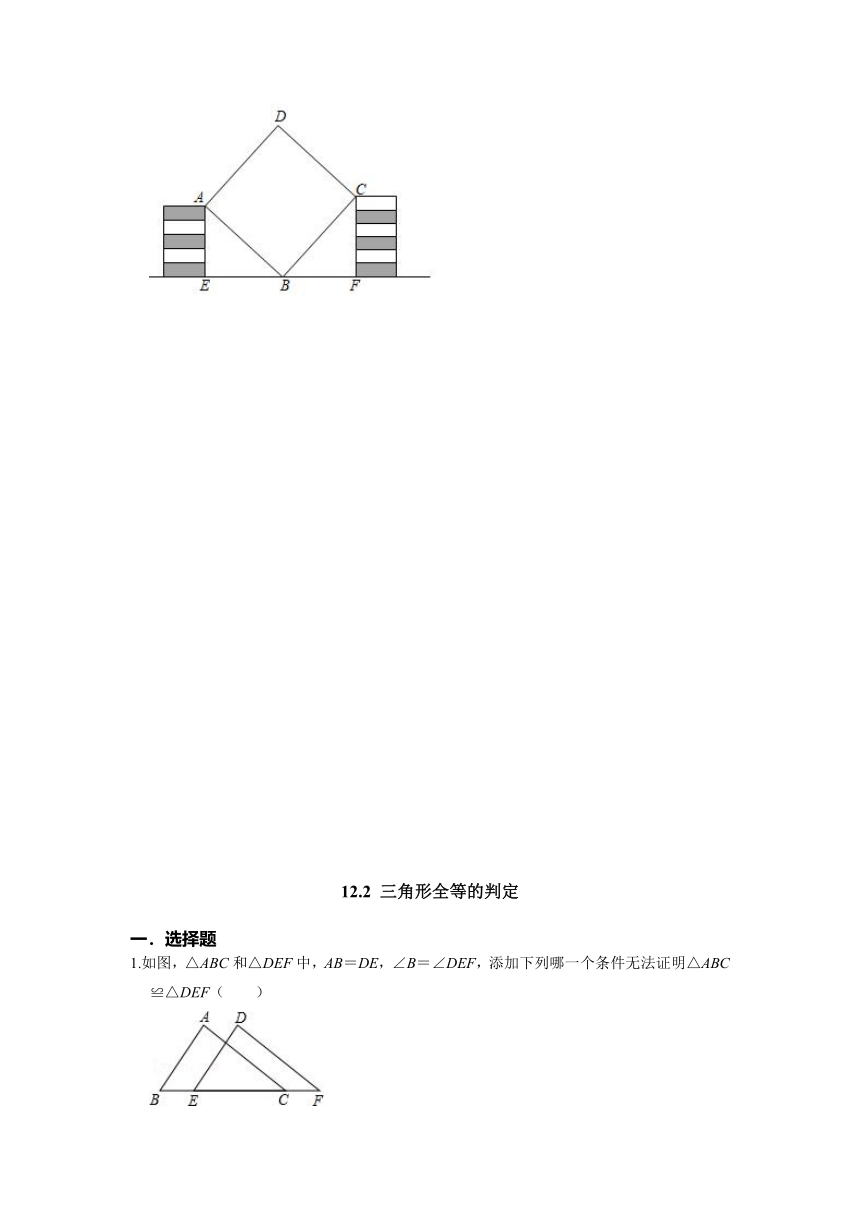
1.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF
B.∠A=∠D
C.AC=DF
D.AC∥DF
2.如图,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE于点D,AE=5cm,BD=2cm,则DE的长是( )
A.8cm
B.5cm
C.3cm
D.2cm
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去
B.带②去
C.带③去
D.①②③都带去
4.如图,AB=AD,DC=BC,E是AC的中点,则图中全等的三角形有( )
A.4对
B.3对
C.2对
D.1对
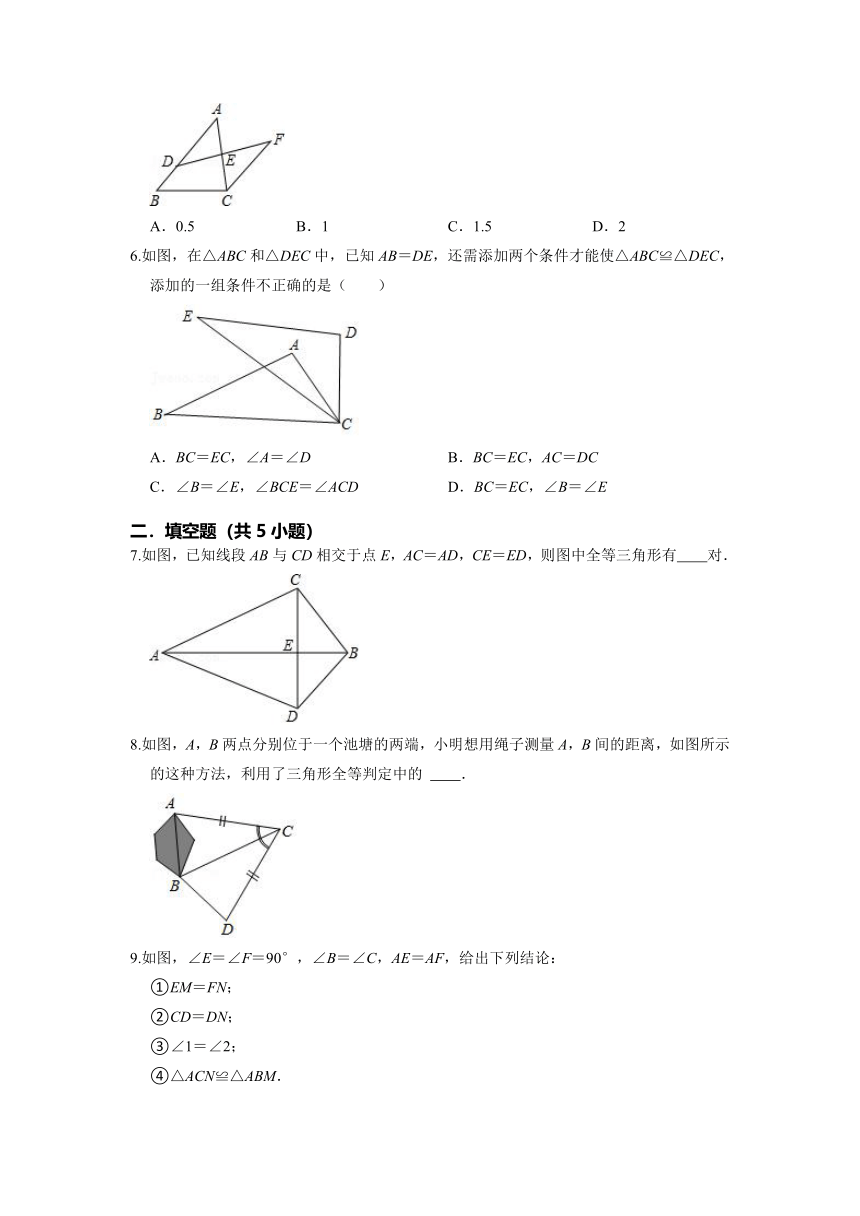
5.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5
B.1
C.1.5
D.2
6.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=EC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
二.填空题(共5小题)
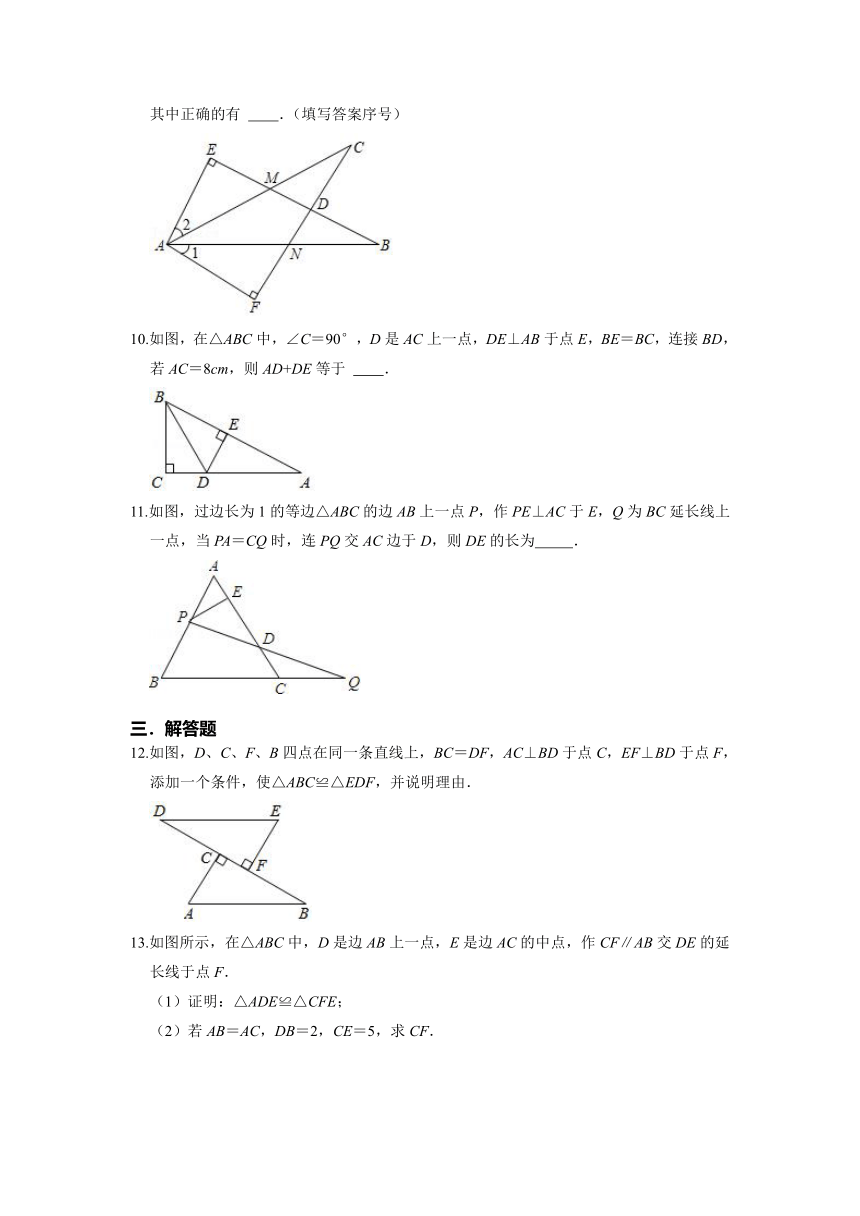
7.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
8.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,利用了三角形全等判定中的
.
9.如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①EM=FN;
②CD=DN;
③∠1=∠2;
④△ACN≌△ABM.
其中正确的有
.(填写答案序号)
10.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,BE=BC,连接BD,若AC=8cm,则AD+DE等于
.
11.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为
.
三.解答题
12.如图,D、C、F、B四点在同一条直线上,BC=DF,AC⊥BD于点C,EF⊥BD于点F,添加一个条件,使△ABC≌△EDF,并说明理由.
13.如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
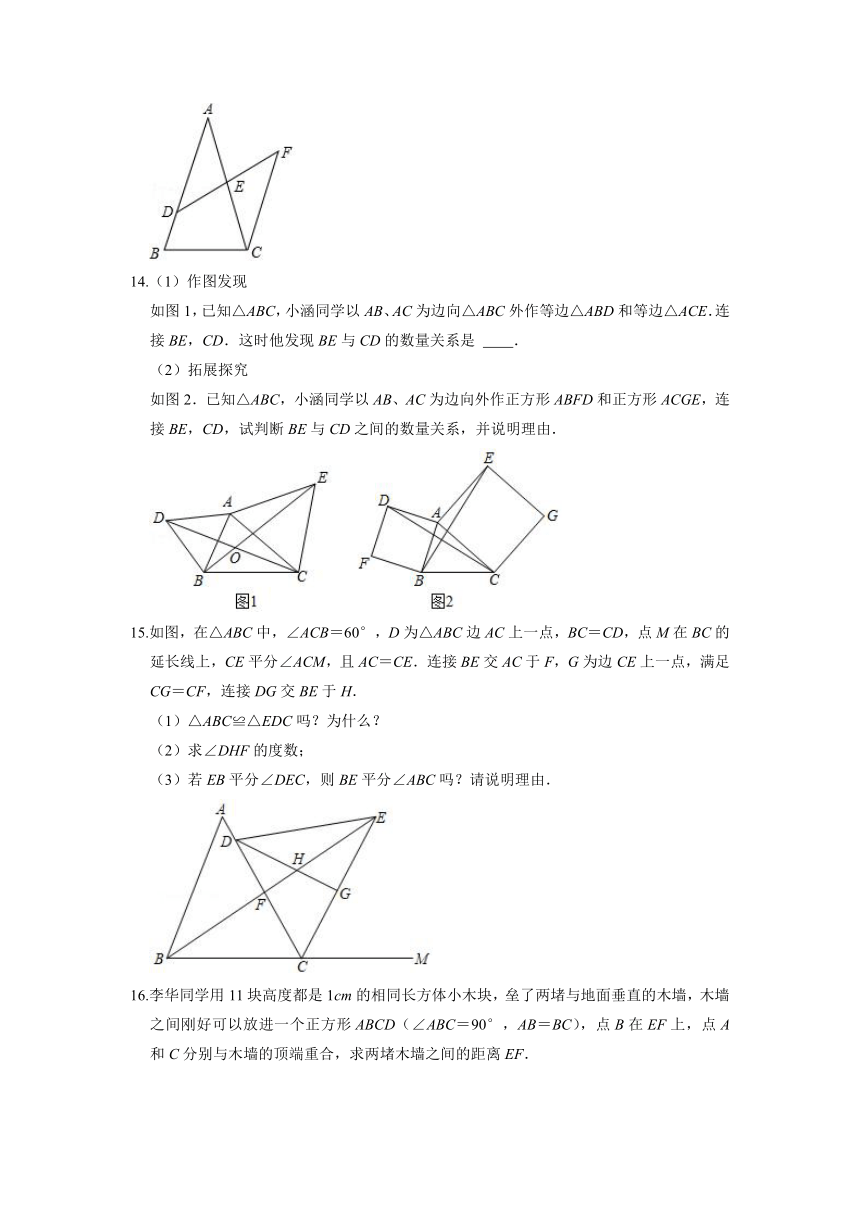
14.(1)作图发现
如图1,已知△ABC,小涵同学以AB、AC为边向△ABC外作等边△ABD和等边△ACE.连接BE,CD.这时他发现BE与CD的数量关系是
.
(2)拓展探究
如图2.已知△ABC,小涵同学以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,试判断BE与CD之间的数量关系,并说明理由.
15.如图,在△ABC中,∠ACB=60°,D为△ABC边AC上一点,BC=CD,点M在BC的延长线上,CE平分∠ACM,且AC=CE.连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
(1)△ABC≌△EDC吗?为什么?
(2)求∠DHF的度数;
(3)若EB平分∠DEC,则BE平分∠ABC吗?请说明理由.
16.李华同学用11块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
12.2
三角形全等的判定
一.选择题
1.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF
B.∠A=∠D
C.AC=DF
D.AC∥DF
【考点】全等三角形的判定.
【答案】C
【分析】根据全等三角形的判定方法对各选项分析判断即可得解.
【解答】解:A、BE=CF可以求出BC=EF,然后利用“SAS”证明△ABC≌△DEF,故本选项错误;
B、∠A=∠D可以利用“ASA”证明△ABC≌△DEF,故本选项错误;
C、AC=DF符合“SSA”,不能证明△ABC≌△DEF,故本选项正确.
D、由AC∥DF可得∠F=∠ACB,然后利用“AAS”证明△ABC≌△DEF,故本选项错误.
故选:C.
2.如图,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE于点D,AE=5cm,BD=2cm,则DE的长是( )
A.8cm
B.5cm
C.3cm
D.2cm
【考点】全等三角形的判定与性质.
【专题】图形的全等.
【答案】C
【分析】根据AAS证明△ACE≌△CBD,可得AE=CD=5cm,CE=BD=2cm,由此即可解决问题;
【解答】解:∵AE⊥CE于点E,BD⊥CE于点D,
∴∠AEC=∠D=∠ACB=90°,
∴∠A+∠ACE=90°,∠ACE+∠BCD=90°,
∴∠A=∠BCD,
∵AC=BC,
∴△ACE≌△CBD(AAS),
∴AE=CD=5cm,CE=BD=2cm,
∴DE=CD﹣CE=5﹣2=3cm.
故选:C.
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去
B.带②去
C.带③去
D.①②③都带去
【考点】全等三角形的应用.
【答案】C
【分析】本题就是已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.
【解答】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
4.如图,AB=AD,DC=BC,E是AC的中点,则图中全等的三角形有( )
A.4对
B.3对
C.2对
D.1对
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形的判定方法,一一判断即可.
【解答】解:有三对全等三角形.
理由:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,∠DCA=∠BCA,
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),
同法可证,△DCE≌△BCE(SAS),
故选:B.
5.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5
B.1
C.1.5
D.2
【考点】全等三角形的判定与性质.
【专题】图形的全等;几何直观;推理能力.
【答案】B
【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=4,CF=3,即可求线段DB的长.
【解答】解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS),
∴AD=CF=3,
∵AB=4,
∴DB=AB﹣AD=4﹣3=1.
故选:B.
6.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=EC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】A
【分析】根据全等三角形的判定定理逐个判断即可.
【解答】解:A.AB=DE,BC=EC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,BC=EC,AB=DE,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
所以∠B=∠E,∠ACB=∠DCE,AB=DE,符合全等三角形的判定定理AAS,能推出△ABC≌△DEC,故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
二.填空题(共5小题)
7.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】3.
【分析】根据全等三角形的判定定理可得出答案.
【解答】解:在△ACE和△ADE中,
,
∴△ACE≌△ADE(SSS),
∴∠CAE=∠DAE,
在△CAB和△DAB中,
∴△CAB≌△DAB(SAS),
∴BC=BD,
在△BCE和△BDE中,
∴△BCE≌△BDE(SSS).
∴图中全等三角形有3对.
故答案为:3.
8.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,利用了三角形全等判定中的
.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】SAS.
【分析】根据SAS证明三角形全等即可.
【解答】解:在△ACB和△DCB中,
,
∴△ACB≌△DCB(SAS),
故答案为:SAS.
9.如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①EM=FN;
②CD=DN;
③∠1=∠2;
④△ACN≌△ABM.
其中正确的有
.(填写答案序号)
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】①③④.
【分析】根据已知条件可以证明在△ABE和△ACF全等,即可得∠1=∠2;
②没有条件可以证明CD=DN,即可判断;
③结合①和已知条件即可得△ACN≌△ABM;
④根据△ABE≌△ACF,可得BE=CF,
【解答】解:在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠EAB=∠FAC,AB=AC,
∴∠EAB﹣∠BAC=∠FAC﹣∠BAC,
∴∠1=∠2.③正确;
在△ACN和△ABM中,
,
∴△ACN≌△ABM(ASA),④正确;
在△AME和△ANF中,
,
∴△AME≌△ANF(ASA),
∴EM=FN,①正确;
没有条件可以证明CD=DN,
∴②错误.
∴其中正确的结论有①③④.
故答案为:①③④.
10.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,BE=BC,连接BD,若AC=8cm,则AD+DE等于
.
【考点】全等三角形的判定与性质.
【专题】三角形;应用意识.
【答案】8cm.
【分析】根据HL证Rt△BCD≌Rt△BED,得出CD=DE,即AD+DE=AD+DC=AC=8cm.
【解答】解:∵∠C=90°,DE⊥AB,
∴∠C=∠BED=90°,
在Rt△BCD和Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴CD=DE,
即AD+DE=AD+DC=AC=8cm,
故答案为:8cm.
11.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为
.
【考点】全等三角形的判定与性质;等边三角形的判定与性质.
【专题】压轴题.
【答案】见试题解答内容
【分析】过P作PF∥BC交AC于F,得出等边三角形APF,推出AP=PF=QC,根据等腰三角形性质求出EF=AE,证△PFD≌△QCD,推出FD=CD,推出DE=AC即可.
【解答】解:过P作PF∥BC交AC于F.
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
∵在△PFD和△QCD中,
,
∴△PFD≌△QCD(AAS),
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,
∴AE+CD=DE=AC,
∵AC=1,
∴DE=.
故答案为:.
三.解答题
12.如图,D、C、F、B四点在同一条直线上,BC=DF,AC⊥BD于点C,EF⊥BD于点F,添加一个条件,使△ABC≌△EDF,并说明理由.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】根据AAS或ASA,可以添加∠D=∠B或∠E=∠A.根据SAS,可以添加EF=AC,根据HL,可以添加DE=AB.
【分析】根据全等三角形的判定方法,解决问题即可.
【解答】解:根据AAS或ASA,可以添加∠D=∠B或∠E=∠A.
理由:∵AC⊥BD于点C,EF⊥BD于点F,
∴∠DFE=∠ACB=90°,
在△DFE和△ACB中,
,
∴△DFE≌△BCA(AAS),
或,
∴△DFE≌△BCA(ASA).
根据SAS,可以添加EF=AC,
理由:在△DFE和△ACB中,
,
∴△DFE≌△BCA(SAS),
根据HL,可以添加DE=AB,
理由:在Rt△DFE和Rt△ACB中,
,
∴△DFE≌△BCA(HL),
13.如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
【考点】全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;图形的全等.
【答案】见试题解答内容
【分析】(1)根据AAS或ASA证明△ADE≌△CFE即可;
(2)由AB=AC,DB=2,CE=5可得AD的长,利用全等三角形的性质求出CF=AD,即可解决问题.
【解答】解:(1)证明:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
∠A=∠ACF,∠ADF=∠F,AE=CE,
∴△ADE≌△CFE(AAS).
(2)∵CE=5,E是边AC的中点,
∴AE=CE=5,
∴AC=10,
∴AB=AC=10,
∴AD=AB﹣BD=10﹣2=8,
∵△ADE≌△CFE,
∴CF=AD=8.
14.(1)作图发现
如图1,已知△ABC,小涵同学以AB、AC为边向△ABC外作等边△ABD和等边△ACE.连接BE,CD.这时他发现BE与CD的数量关系是
.
(2)拓展探究
如图2.已知△ABC,小涵同学以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,试判断BE与CD之间的数量关系,并说明理由.
【考点】四边形综合题.
【专题】图形的全等;推理能力.
【答案】(1)CD=BE;(2)CD=BE,理由见解答过程.
【分析】(1)根据△ABD和△ACE都是等边三角形,可通过SAS证明△ADC≌△ABE,得CD=BE;
(2)根据四边形ABFD和四边形ACGE是正方形,可通过SAS证明△ADC≌△ABE,得CD=BE.
【解答】解:(1)∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∴∠DAC=∠BAE,
在△ADC和△ABE中,
,
∴△ADC≌△ABE(SAS),
∴CD=BE,
故答案为:CD=BE.
(2)BE=CD,理由如下:
∵四边形ABFD和四边形ACGE是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAC=∠BAE,
在△ADC和△ABE中,
,
∴△ADC≌△ABE(SAS),
∴CD=BE.
15.如图,在△ABC中,∠ACB=60°,D为△ABC边AC上一点,BC=CD,点M在BC的延长线上,CE平分∠ACM,且AC=CE.连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
(1)△ABC≌△EDC吗?为什么?
(2)求∠DHF的度数;
(3)若EB平分∠DEC,则BE平分∠ABC吗?请说明理由.
【考点】全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】(1)△ABC≌△EDC,理由见解析;
(2)60°;
(3)BE平分∠ABC.理由见解析.
【分析】(1)由“SAS”可证△ABC≌△EDC;
(2)由“SAS”可证△CDG≌△CBF,可得∠CBF=∠CDG,再利用三角形的内角和定理,得∠CBF+∠BCF=∠CDG+∠DHF,又∠ACB=60°,即可出∠DHF=∠ACB=60°,从而问题得以解决;
(3)由三角形的内角和可得∠DEB+∠EBC=60°,因为∠DEB=∠BEC,只要证出∠DEB+∠ABE=60°,用三角形的外角以及等量代换可以证出,进而得到BE平分∠ABC.
【解答】解:(1)△ABC≌△EDC.
理由:
∵CA平分∠BCE,
∴∠ACB=∠ACE,
∵AC=CE,BC=CD,
∴△ABC≌△EDC(SAS);
(2)在△CDG和△CBF中,
,
∴△CDG≌△CBF(SAS),
∴∠CBF=∠CDG,
∵∠DFH=∠BFC,
∴∠DHF=∠BCF=60°;
(3)BE平分∠ABC.
理由:由(1)得△ABC≌△EDC,
∴∠ABC=∠EDC,
∵∠ACB=∠DCE=60°,
∴∠BEC+∠CBE=60°,
又∵∠DFH=∠A+∠ABE=∠BEC+∠FCG,
∵∠A=∠DEC=2∠DEB=2∠BEC,
∴2∠DEB+∠ABE=∠BEC+60°,
∴∠DEB+∠ABE=60°,
∴∠ABE=∠CBE,
即BE平分∠ABC.
16.李华同学用11块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
【考点】全等三角形的应用.
【专题】图形的全等;应用意识.
【答案】11cm.
【分析】根据∠ABE的余角相等求出∠EAB=∠CBF,然后利用“角角边”证明△ABE和△BCF全等,根据全等三角形对应边相等可得AE=BF,BE=CF,于是得到结论.
【解答】解:∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,
∵∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=5cm,BE=CF=6cm,
∴EF=5+6=11(cm).
三角形全等的判定
一.选择题
1.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF
B.∠A=∠D
C.AC=DF
D.AC∥DF
2.如图,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE于点D,AE=5cm,BD=2cm,则DE的长是( )
A.8cm
B.5cm
C.3cm
D.2cm
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去
B.带②去
C.带③去
D.①②③都带去
4.如图,AB=AD,DC=BC,E是AC的中点,则图中全等的三角形有( )
A.4对
B.3对
C.2对
D.1对
5.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5
B.1
C.1.5
D.2
6.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=EC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
二.填空题(共5小题)
7.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
8.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,利用了三角形全等判定中的
.
9.如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①EM=FN;
②CD=DN;
③∠1=∠2;
④△ACN≌△ABM.
其中正确的有
.(填写答案序号)
10.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,BE=BC,连接BD,若AC=8cm,则AD+DE等于
.
11.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为
.
三.解答题
12.如图,D、C、F、B四点在同一条直线上,BC=DF,AC⊥BD于点C,EF⊥BD于点F,添加一个条件,使△ABC≌△EDF,并说明理由.
13.如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
14.(1)作图发现
如图1,已知△ABC,小涵同学以AB、AC为边向△ABC外作等边△ABD和等边△ACE.连接BE,CD.这时他发现BE与CD的数量关系是
.
(2)拓展探究
如图2.已知△ABC,小涵同学以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,试判断BE与CD之间的数量关系,并说明理由.
15.如图,在△ABC中,∠ACB=60°,D为△ABC边AC上一点,BC=CD,点M在BC的延长线上,CE平分∠ACM,且AC=CE.连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
(1)△ABC≌△EDC吗?为什么?
(2)求∠DHF的度数;
(3)若EB平分∠DEC,则BE平分∠ABC吗?请说明理由.
16.李华同学用11块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
12.2
三角形全等的判定
一.选择题
1.如图,△ABC和△DEF中,AB=DE,∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.BE=CF
B.∠A=∠D
C.AC=DF
D.AC∥DF
【考点】全等三角形的判定.
【答案】C
【分析】根据全等三角形的判定方法对各选项分析判断即可得解.
【解答】解:A、BE=CF可以求出BC=EF,然后利用“SAS”证明△ABC≌△DEF,故本选项错误;
B、∠A=∠D可以利用“ASA”证明△ABC≌△DEF,故本选项错误;
C、AC=DF符合“SSA”,不能证明△ABC≌△DEF,故本选项正确.
D、由AC∥DF可得∠F=∠ACB,然后利用“AAS”证明△ABC≌△DEF,故本选项错误.
故选:C.
2.如图,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE于点D,AE=5cm,BD=2cm,则DE的长是( )
A.8cm
B.5cm
C.3cm
D.2cm
【考点】全等三角形的判定与性质.
【专题】图形的全等.
【答案】C
【分析】根据AAS证明△ACE≌△CBD,可得AE=CD=5cm,CE=BD=2cm,由此即可解决问题;
【解答】解:∵AE⊥CE于点E,BD⊥CE于点D,
∴∠AEC=∠D=∠ACB=90°,
∴∠A+∠ACE=90°,∠ACE+∠BCD=90°,
∴∠A=∠BCD,
∵AC=BC,
∴△ACE≌△CBD(AAS),
∴AE=CD=5cm,CE=BD=2cm,
∴DE=CD﹣CE=5﹣2=3cm.
故选:C.
3.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去
B.带②去
C.带③去
D.①②③都带去
【考点】全等三角形的应用.
【答案】C
【分析】本题就是已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.
【解答】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
4.如图,AB=AD,DC=BC,E是AC的中点,则图中全等的三角形有( )
A.4对
B.3对
C.2对
D.1对
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据全等三角形的判定方法,一一判断即可.
【解答】解:有三对全等三角形.
理由:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,∠DCA=∠BCA,
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),
同法可证,△DCE≌△BCE(SAS),
故选:B.
5.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5
B.1
C.1.5
D.2
【考点】全等三角形的判定与性质.
【专题】图形的全等;几何直观;推理能力.
【答案】B
【分析】根据平行线的性质,得出∠A=∠FCE,∠ADE=∠F,根据全等三角形的判定,得出△ADE≌△CFE,根据全等三角形的性质,得出AD=CF,根据AB=4,CF=3,即可求线段DB的长.
【解答】解:∵CF∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS),
∴AD=CF=3,
∵AB=4,
∴DB=AB﹣AD=4﹣3=1.
故选:B.
6.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件不正确的是( )
A.BC=EC,∠A=∠D
B.BC=EC,AC=DC
C.∠B=∠E,∠BCE=∠ACD
D.BC=EC,∠B=∠E
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】A
【分析】根据全等三角形的判定定理逐个判断即可.
【解答】解:A.AB=DE,BC=EC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,BC=EC,AB=DE,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
所以∠B=∠E,∠ACB=∠DCE,AB=DE,符合全等三角形的判定定理AAS,能推出△ABC≌△DEC,故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故选:A.
二.填空题(共5小题)
7.如图,已知线段AB与CD相交于点E,AC=AD,CE=ED,则图中全等三角形有 对.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】3.
【分析】根据全等三角形的判定定理可得出答案.
【解答】解:在△ACE和△ADE中,
,
∴△ACE≌△ADE(SSS),
∴∠CAE=∠DAE,
在△CAB和△DAB中,
∴△CAB≌△DAB(SAS),
∴BC=BD,
在△BCE和△BDE中,
∴△BCE≌△BDE(SSS).
∴图中全等三角形有3对.
故答案为:3.
8.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,利用了三角形全等判定中的
.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】SAS.
【分析】根据SAS证明三角形全等即可.
【解答】解:在△ACB和△DCB中,
,
∴△ACB≌△DCB(SAS),
故答案为:SAS.
9.如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①EM=FN;
②CD=DN;
③∠1=∠2;
④△ACN≌△ABM.
其中正确的有
.(填写答案序号)
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】①③④.
【分析】根据已知条件可以证明在△ABE和△ACF全等,即可得∠1=∠2;
②没有条件可以证明CD=DN,即可判断;
③结合①和已知条件即可得△ACN≌△ABM;
④根据△ABE≌△ACF,可得BE=CF,
【解答】解:在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS),
∴∠EAB=∠FAC,AB=AC,
∴∠EAB﹣∠BAC=∠FAC﹣∠BAC,
∴∠1=∠2.③正确;
在△ACN和△ABM中,
,
∴△ACN≌△ABM(ASA),④正确;
在△AME和△ANF中,
,
∴△AME≌△ANF(ASA),
∴EM=FN,①正确;
没有条件可以证明CD=DN,
∴②错误.
∴其中正确的结论有①③④.
故答案为:①③④.
10.如图,在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于点E,BE=BC,连接BD,若AC=8cm,则AD+DE等于
.
【考点】全等三角形的判定与性质.
【专题】三角形;应用意识.
【答案】8cm.
【分析】根据HL证Rt△BCD≌Rt△BED,得出CD=DE,即AD+DE=AD+DC=AC=8cm.
【解答】解:∵∠C=90°,DE⊥AB,
∴∠C=∠BED=90°,
在Rt△BCD和Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴CD=DE,
即AD+DE=AD+DC=AC=8cm,
故答案为:8cm.
11.如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为
.
【考点】全等三角形的判定与性质;等边三角形的判定与性质.
【专题】压轴题.
【答案】见试题解答内容
【分析】过P作PF∥BC交AC于F,得出等边三角形APF,推出AP=PF=QC,根据等腰三角形性质求出EF=AE,证△PFD≌△QCD,推出FD=CD,推出DE=AC即可.
【解答】解:过P作PF∥BC交AC于F.
∵PF∥BC,△ABC是等边三角形,
∴∠PFD=∠QCD,△APF是等边三角形,
∴AP=PF=AF,
∵PE⊥AC,
∴AE=EF,
∵AP=PF,AP=CQ,
∴PF=CQ.
∵在△PFD和△QCD中,
,
∴△PFD≌△QCD(AAS),
∴FD=CD,
∵AE=EF,
∴EF+FD=AE+CD,
∴AE+CD=DE=AC,
∵AC=1,
∴DE=.
故答案为:.
三.解答题
12.如图,D、C、F、B四点在同一条直线上,BC=DF,AC⊥BD于点C,EF⊥BD于点F,添加一个条件,使△ABC≌△EDF,并说明理由.
【考点】全等三角形的判定.
【专题】图形的全等;推理能力.
【答案】根据AAS或ASA,可以添加∠D=∠B或∠E=∠A.根据SAS,可以添加EF=AC,根据HL,可以添加DE=AB.
【分析】根据全等三角形的判定方法,解决问题即可.
【解答】解:根据AAS或ASA,可以添加∠D=∠B或∠E=∠A.
理由:∵AC⊥BD于点C,EF⊥BD于点F,
∴∠DFE=∠ACB=90°,
在△DFE和△ACB中,
,
∴△DFE≌△BCA(AAS),
或,
∴△DFE≌△BCA(ASA).
根据SAS,可以添加EF=AC,
理由:在△DFE和△ACB中,
,
∴△DFE≌△BCA(SAS),
根据HL,可以添加DE=AB,
理由:在Rt△DFE和Rt△ACB中,
,
∴△DFE≌△BCA(HL),
13.如图所示,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若AB=AC,DB=2,CE=5,求CF.
【考点】全等三角形的判定与性质.
【专题】线段、角、相交线与平行线;图形的全等.
【答案】见试题解答内容
【分析】(1)根据AAS或ASA证明△ADE≌△CFE即可;
(2)由AB=AC,DB=2,CE=5可得AD的长,利用全等三角形的性质求出CF=AD,即可解决问题.
【解答】解:(1)证明:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
∠A=∠ACF,∠ADF=∠F,AE=CE,
∴△ADE≌△CFE(AAS).
(2)∵CE=5,E是边AC的中点,
∴AE=CE=5,
∴AC=10,
∴AB=AC=10,
∴AD=AB﹣BD=10﹣2=8,
∵△ADE≌△CFE,
∴CF=AD=8.
14.(1)作图发现
如图1,已知△ABC,小涵同学以AB、AC为边向△ABC外作等边△ABD和等边△ACE.连接BE,CD.这时他发现BE与CD的数量关系是
.
(2)拓展探究
如图2.已知△ABC,小涵同学以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,试判断BE与CD之间的数量关系,并说明理由.
【考点】四边形综合题.
【专题】图形的全等;推理能力.
【答案】(1)CD=BE;(2)CD=BE,理由见解答过程.
【分析】(1)根据△ABD和△ACE都是等边三角形,可通过SAS证明△ADC≌△ABE,得CD=BE;
(2)根据四边形ABFD和四边形ACGE是正方形,可通过SAS证明△ADC≌△ABE,得CD=BE.
【解答】解:(1)∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∴∠DAC=∠BAE,
在△ADC和△ABE中,
,
∴△ADC≌△ABE(SAS),
∴CD=BE,
故答案为:CD=BE.
(2)BE=CD,理由如下:
∵四边形ABFD和四边形ACGE是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°,
∴∠DAC=∠BAE,
在△ADC和△ABE中,
,
∴△ADC≌△ABE(SAS),
∴CD=BE.
15.如图,在△ABC中,∠ACB=60°,D为△ABC边AC上一点,BC=CD,点M在BC的延长线上,CE平分∠ACM,且AC=CE.连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
(1)△ABC≌△EDC吗?为什么?
(2)求∠DHF的度数;
(3)若EB平分∠DEC,则BE平分∠ABC吗?请说明理由.
【考点】全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】(1)△ABC≌△EDC,理由见解析;
(2)60°;
(3)BE平分∠ABC.理由见解析.
【分析】(1)由“SAS”可证△ABC≌△EDC;
(2)由“SAS”可证△CDG≌△CBF,可得∠CBF=∠CDG,再利用三角形的内角和定理,得∠CBF+∠BCF=∠CDG+∠DHF,又∠ACB=60°,即可出∠DHF=∠ACB=60°,从而问题得以解决;
(3)由三角形的内角和可得∠DEB+∠EBC=60°,因为∠DEB=∠BEC,只要证出∠DEB+∠ABE=60°,用三角形的外角以及等量代换可以证出,进而得到BE平分∠ABC.
【解答】解:(1)△ABC≌△EDC.
理由:
∵CA平分∠BCE,
∴∠ACB=∠ACE,
∵AC=CE,BC=CD,
∴△ABC≌△EDC(SAS);
(2)在△CDG和△CBF中,
,
∴△CDG≌△CBF(SAS),
∴∠CBF=∠CDG,
∵∠DFH=∠BFC,
∴∠DHF=∠BCF=60°;
(3)BE平分∠ABC.
理由:由(1)得△ABC≌△EDC,
∴∠ABC=∠EDC,
∵∠ACB=∠DCE=60°,
∴∠BEC+∠CBE=60°,
又∵∠DFH=∠A+∠ABE=∠BEC+∠FCG,
∵∠A=∠DEC=2∠DEB=2∠BEC,
∴2∠DEB+∠ABE=∠BEC+60°,
∴∠DEB+∠ABE=60°,
∴∠ABE=∠CBE,
即BE平分∠ABC.
16.李华同学用11块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
【考点】全等三角形的应用.
【专题】图形的全等;应用意识.
【答案】11cm.
【分析】根据∠ABE的余角相等求出∠EAB=∠CBF,然后利用“角角边”证明△ABE和△BCF全等,根据全等三角形对应边相等可得AE=BF,BE=CF,于是得到结论.
【解答】解:∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,
∵∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=5cm,BE=CF=6cm,
∴EF=5+6=11(cm).
