2.1.1用字母表示数同步练习-2021-2022学年七年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 2.1.1用字母表示数同步练习-2021-2022学年七年级数学人教版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 127.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 17:53:01 | ||
图片预览


文档简介
(人教版)-2021-2-22七年级上册教材同步练习
第二章
2.1.1用字母表示数
一、单选题
1.一个两位数,它的十位数字是,个位数字是,那么这个两位数是(
).
A.
B.
C.
D.
2.下列代数式书写正确的是( )
A.
B.
C.
D.
3.下列式子中,符合代数式书写格式的是(
)
A.m÷﹣2n
B.
C.a×5
D.
4.下列式子:,,
,,,其中的代数式有(
)
A.个
B.个
C.个
D.个
5.某商品先在批发价m元的基础上提高10%零售,后又降价10%出售,则按后面的售价每销售一件商品的盈亏情况为(
).
A.亏损了
B.盈利了
C.不亏不盈
D.盈亏不确定
二、填空题
6.有煤3000千克,每天用去x千克,10
天后剩余_______千克.
7.一个两位数,二个数位上数字之和为,若个位上的数字为2,则这个两位数为_______.
8.三个连续奇数,中间一个是n,则它们的积是______.
9.2x+3y可以解释为__________
三、解答题
10.判断下列各式中哪些是代数式,哪些不是代数式?
0,,F=ma,m+2>m,2x2﹣3x+11,,13≠12,,﹣y,6π.
11.植树节期间,某校植树,七年级种棵,八年级种的比七年级种的树的2倍还多4棵,九年级种的比八年级种的树的一半多3棵.
(1)九年级种树多少棵?
(2)三个年级一共种树多少棵?
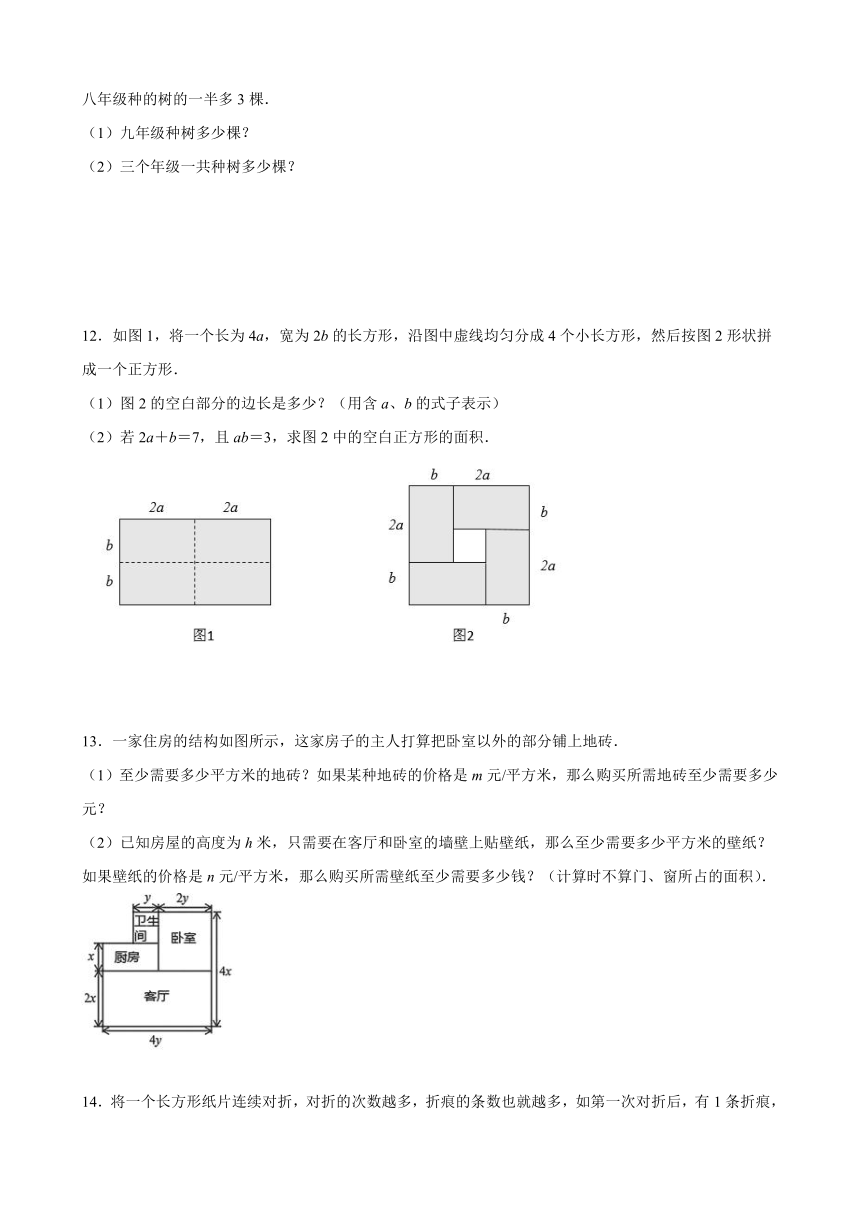
12.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
13.一家住房的结构如图所示,这家房子的主人打算把卧室以外的部分铺上地砖.
(1)至少需要多少平方米的地砖?如果某种地砖的价格是m元/平方米,那么购买所需地砖至少需要多少元?
(2)已知房屋的高度为h米,只需要在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果壁纸的价格是n元/平方米,那么购买所需壁纸至少需要多少钱?(计算时不算门、窗所占的面积).
14.将一个长方形纸片连续对折,对折的次数越多,折痕的条数也就越多,如第一次对折后,有1条折痕,第2次对折后,共有3条折痕.
(1)第3次对折后共有多少条折痕?第4次对折后呢?
(2)对折多少次后折痕会超过100条?
(3)请找出折痕条数与对折次数的对应规律,写出对折n次后,折痕有多少条?
15.某玩具厂出售一种玩具,其成本价每件28元,现有两种方式销售.
方式1:直接由玩具厂的门市部销售,每件产品售价为40元,同时每月还要支出其他费用3600元;
方式2:委托某一商场销售,出厂价定为每件35元.
(1)若每个月销售x件,则方式1可获得利润为
,方式2可获得利润为
;
(2)若每个月销售量达到2000件时,采用哪种销售方式获得利润较多?
(3)请列一元一次方程求解:每个月销售多少件时,两种销售方式所得利润相等?
参考答案
1.D
【解析】解:∵一个两位数,它的十位数是,个位数字是,
∴根据两位数的表示方法,这个两位数表示为:.
故选:
2.D
【解析】解:(A)的正确书写是4a,故A错误;
(B)m÷n的正确书写是
,故B错误;
(C)的正确书写是,故C错误;
(D)书写正确,故D符合题意;
故选:D.
3.B
【解析】A:正确的书写格式是,不符合题意;
B:
符合代数式书写格式,符合题意;
C:
正确的书写格式是5a,不符合题意;
D:正确的书写格式是,不符合题意;
故选:B.
4.C
【解析】解:由代数式的定义可知是代数式的有,,,,共4个,
而因为有等号,是等式,不是代数式,
故选:C.
5.A
【解析】由题意得,后面的售价为:m×(1+10%)×(1-10%)=0.99m元
∵m>0,
∴m>0.99m,
∴按后面的售价每销售一件商品,为亏损情况
故选:A.
6.3000-10x
【解析】解:3000-10x=3000-10x(千克).
故答案为:3000-10x
7.10x-18.
【解析】解:∵二个数位上数字之和为,个位上的数字为2
∴十位上的数为x-2
∴这个两位数是10(x-2)+2=10x-18.
故答案为10x-18.
8.
【解析】解:由中间的数为n知,最小的奇数是,最大的奇数是,那么有:
.
故答案为:.
9.x的2倍与y的3倍的和
【解析】2x+3y可以解释为x的2倍与y的3倍的和
故答案为:x的2倍与y的3倍的和.
10.代数式的有:0,,2x2﹣3x+11,,,﹣y,6π.
不是代数式的有:F=ma,m+2>m,13≠12.
【解析】代数式的有:0,,2x2﹣3x+11,,,﹣y,6π;
不是代数式的有:F=ma,m+2>m,13≠12.
11.(1)(m+5)棵;(2)(4m+9)棵.
【解析】解:(1)∵七年级种棵,八年级种的比七年级种的树的2倍还多4棵
∴八年级种树(2m+4)棵
∵九年级种的比八年级种的树的一半多3棵
∴九年级种树=m+5(棵)
(2)由(1)可知八年级种树(2m+4)棵,九年级种树(m+5)棵
∴三个年级一共种树=
m+2m+4+m+5=4m+9(棵)
12.(1)2a-b;(2)25
【解析】解:(1)图2的空白部分的边长是2a-b;
(2)由图21-2可知,小正方形的面积=大正方形的面积-4个小长方形的面积,
∵大正方形的边长=2a+b=7,
∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a-b)2=49-24=25.
13.(1)11mxy元;(2)(8xhn+12yhn)元
【解析】解:(1)根据题意得:xy+2xy+8xy=11xy(m2),
则把卧室以外的部分都铺上地砖,至少需要11xym2的地砖;购买所需地砖至少需要11mxy元;
(2)根据题意得:(8x+12y)h=(8xh+12yh)m2,
则在客厅和卧室的墙壁上贴壁纸,那么至少需要(8xh+12yh)平方米的壁纸,至少需要(8xhn+12yhn)元.
14.(1)第3次对折后共有7条折痕,第4次对折后有15条折痕;(2)对折7次后折痕会超过100条;(3)对折n次后,折痕有条.
【解析】(1)动手操作可知,第3次对折后的折痕条数为7条,
第4次对折后的折痕条数为15条;
(2)观察可知,第1次对折后的折痕条数为条,
第2次对折后的折痕条数为条,
第3次对折后的折痕条数为条,
第4次对折后的折痕条数为条,
归纳类推得:第n次对折后的折痕条数为条,
因为,
所以对折7次后折痕会超过100条;
(3)由(2)已得:对折n次后的折痕条数为条.
15.(1);;(2)采用方式1直接由厂家门市部出售的利润较多;(3)每月销售720件时,两种销售方式所得利润相等.
【解析】(1)按方式1销售时的利润是:(40?28)x?3600即12x?3600;
按方式2销售时的时利润是(35?28)x即7x,
故答案为:;
(2)当每月销售达2000件时,方式1出售的利润为:(40-28)×2000-3600=20400(元),
方式2销售的利润为:(35-28)×2000=14000(元),
∵20400>14000,
采用方式1直接由厂家门市部出售的利润较多。
(3)设每月销售x件时,所得利润相同,
根据题意可得:12x-3600=7x(或(40-28)x-3600=(35-28)x)
解得:x=720.
答:每月销售720件时,所得利润相同.
第二章
2.1.1用字母表示数
一、单选题
1.一个两位数,它的十位数字是,个位数字是,那么这个两位数是(
).
A.
B.
C.
D.
2.下列代数式书写正确的是( )
A.
B.
C.
D.
3.下列式子中,符合代数式书写格式的是(
)
A.m÷﹣2n
B.
C.a×5
D.
4.下列式子:,,
,,,其中的代数式有(
)
A.个
B.个
C.个
D.个
5.某商品先在批发价m元的基础上提高10%零售,后又降价10%出售,则按后面的售价每销售一件商品的盈亏情况为(
).
A.亏损了
B.盈利了
C.不亏不盈
D.盈亏不确定
二、填空题
6.有煤3000千克,每天用去x千克,10
天后剩余_______千克.
7.一个两位数,二个数位上数字之和为,若个位上的数字为2,则这个两位数为_______.
8.三个连续奇数,中间一个是n,则它们的积是______.
9.2x+3y可以解释为__________
三、解答题
10.判断下列各式中哪些是代数式,哪些不是代数式?
0,,F=ma,m+2>m,2x2﹣3x+11,,13≠12,,﹣y,6π.
11.植树节期间,某校植树,七年级种棵,八年级种的比七年级种的树的2倍还多4棵,九年级种的比八年级种的树的一半多3棵.
(1)九年级种树多少棵?
(2)三个年级一共种树多少棵?
12.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
13.一家住房的结构如图所示,这家房子的主人打算把卧室以外的部分铺上地砖.
(1)至少需要多少平方米的地砖?如果某种地砖的价格是m元/平方米,那么购买所需地砖至少需要多少元?
(2)已知房屋的高度为h米,只需要在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果壁纸的价格是n元/平方米,那么购买所需壁纸至少需要多少钱?(计算时不算门、窗所占的面积).
14.将一个长方形纸片连续对折,对折的次数越多,折痕的条数也就越多,如第一次对折后,有1条折痕,第2次对折后,共有3条折痕.
(1)第3次对折后共有多少条折痕?第4次对折后呢?
(2)对折多少次后折痕会超过100条?
(3)请找出折痕条数与对折次数的对应规律,写出对折n次后,折痕有多少条?
15.某玩具厂出售一种玩具,其成本价每件28元,现有两种方式销售.
方式1:直接由玩具厂的门市部销售,每件产品售价为40元,同时每月还要支出其他费用3600元;
方式2:委托某一商场销售,出厂价定为每件35元.
(1)若每个月销售x件,则方式1可获得利润为
,方式2可获得利润为
;
(2)若每个月销售量达到2000件时,采用哪种销售方式获得利润较多?
(3)请列一元一次方程求解:每个月销售多少件时,两种销售方式所得利润相等?
参考答案
1.D
【解析】解:∵一个两位数,它的十位数是,个位数字是,
∴根据两位数的表示方法,这个两位数表示为:.
故选:
2.D
【解析】解:(A)的正确书写是4a,故A错误;
(B)m÷n的正确书写是
,故B错误;
(C)的正确书写是,故C错误;
(D)书写正确,故D符合题意;
故选:D.
3.B
【解析】A:正确的书写格式是,不符合题意;
B:
符合代数式书写格式,符合题意;
C:
正确的书写格式是5a,不符合题意;
D:正确的书写格式是,不符合题意;
故选:B.
4.C
【解析】解:由代数式的定义可知是代数式的有,,,,共4个,
而因为有等号,是等式,不是代数式,
故选:C.
5.A
【解析】由题意得,后面的售价为:m×(1+10%)×(1-10%)=0.99m元
∵m>0,
∴m>0.99m,
∴按后面的售价每销售一件商品,为亏损情况
故选:A.
6.3000-10x
【解析】解:3000-10x=3000-10x(千克).
故答案为:3000-10x
7.10x-18.
【解析】解:∵二个数位上数字之和为,个位上的数字为2
∴十位上的数为x-2
∴这个两位数是10(x-2)+2=10x-18.
故答案为10x-18.
8.
【解析】解:由中间的数为n知,最小的奇数是,最大的奇数是,那么有:
.
故答案为:.
9.x的2倍与y的3倍的和
【解析】2x+3y可以解释为x的2倍与y的3倍的和
故答案为:x的2倍与y的3倍的和.
10.代数式的有:0,,2x2﹣3x+11,,,﹣y,6π.
不是代数式的有:F=ma,m+2>m,13≠12.
【解析】代数式的有:0,,2x2﹣3x+11,,,﹣y,6π;
不是代数式的有:F=ma,m+2>m,13≠12.
11.(1)(m+5)棵;(2)(4m+9)棵.
【解析】解:(1)∵七年级种棵,八年级种的比七年级种的树的2倍还多4棵
∴八年级种树(2m+4)棵
∵九年级种的比八年级种的树的一半多3棵
∴九年级种树=m+5(棵)
(2)由(1)可知八年级种树(2m+4)棵,九年级种树(m+5)棵
∴三个年级一共种树=
m+2m+4+m+5=4m+9(棵)
12.(1)2a-b;(2)25
【解析】解:(1)图2的空白部分的边长是2a-b;
(2)由图21-2可知,小正方形的面积=大正方形的面积-4个小长方形的面积,
∵大正方形的边长=2a+b=7,
∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a-b)2=49-24=25.
13.(1)11mxy元;(2)(8xhn+12yhn)元
【解析】解:(1)根据题意得:xy+2xy+8xy=11xy(m2),
则把卧室以外的部分都铺上地砖,至少需要11xym2的地砖;购买所需地砖至少需要11mxy元;
(2)根据题意得:(8x+12y)h=(8xh+12yh)m2,
则在客厅和卧室的墙壁上贴壁纸,那么至少需要(8xh+12yh)平方米的壁纸,至少需要(8xhn+12yhn)元.
14.(1)第3次对折后共有7条折痕,第4次对折后有15条折痕;(2)对折7次后折痕会超过100条;(3)对折n次后,折痕有条.
【解析】(1)动手操作可知,第3次对折后的折痕条数为7条,
第4次对折后的折痕条数为15条;
(2)观察可知,第1次对折后的折痕条数为条,
第2次对折后的折痕条数为条,
第3次对折后的折痕条数为条,
第4次对折后的折痕条数为条,
归纳类推得:第n次对折后的折痕条数为条,
因为,
所以对折7次后折痕会超过100条;
(3)由(2)已得:对折n次后的折痕条数为条.
15.(1);;(2)采用方式1直接由厂家门市部出售的利润较多;(3)每月销售720件时,两种销售方式所得利润相等.
【解析】(1)按方式1销售时的利润是:(40?28)x?3600即12x?3600;
按方式2销售时的时利润是(35?28)x即7x,
故答案为:;
(2)当每月销售达2000件时,方式1出售的利润为:(40-28)×2000-3600=20400(元),
方式2销售的利润为:(35-28)×2000=14000(元),
∵20400>14000,
采用方式1直接由厂家门市部出售的利润较多。
(3)设每月销售x件时,所得利润相同,
根据题意可得:12x-3600=7x(或(40-28)x-3600=(35-28)x)
解得:x=720.
答:每月销售720件时,所得利润相同.
