北师大版八年级数学上册4.4一次函数的应用一课一练 (word版含答案)
文档属性
| 名称 | 北师大版八年级数学上册4.4一次函数的应用一课一练 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 104.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 07:45:31 | ||
图片预览


文档简介
4.4《一次函数的应用》习题2
一、选择题
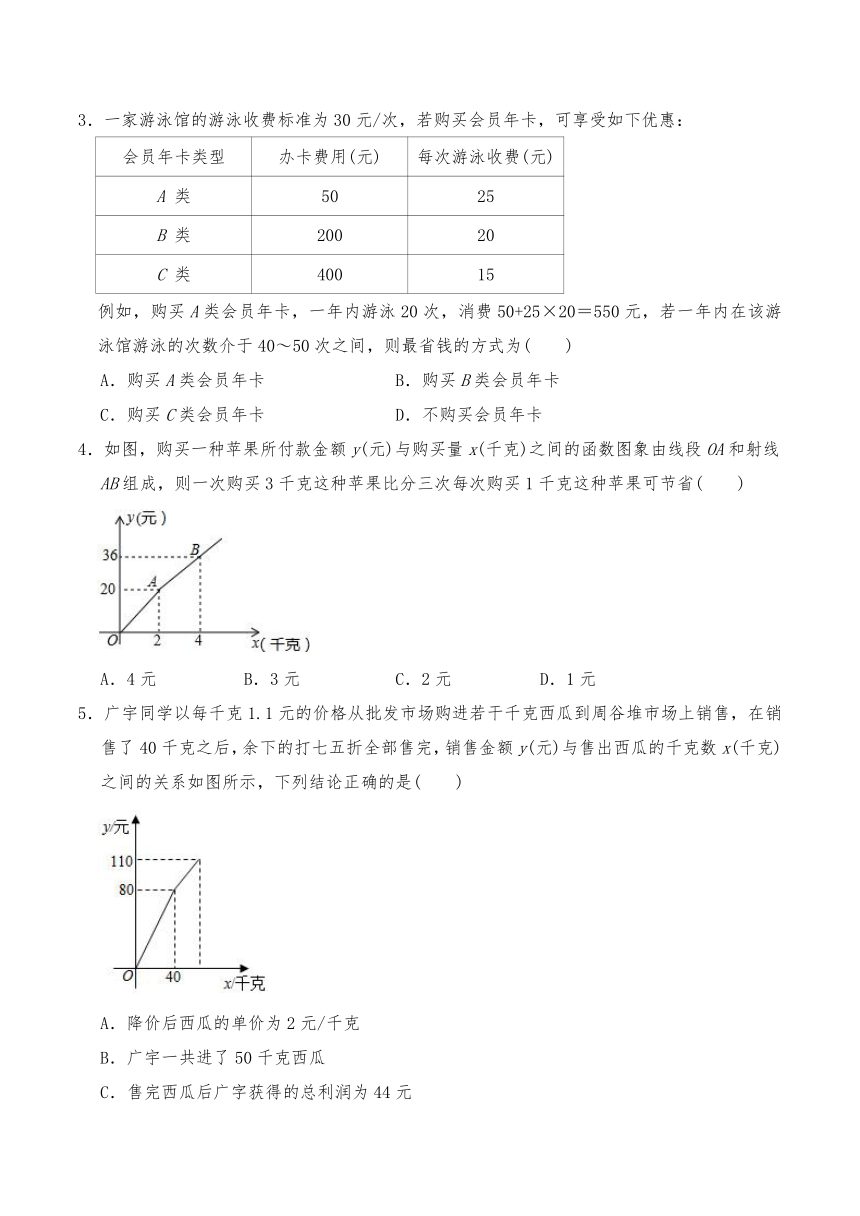
1.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为xkg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5kg后,超过的部分价格优惠是打五折
D.若顾客采摘12kg草莓,那么到甲园或乙园的总费用相同
2.某公司为调动职工工作积极性,向工会代言人提供了两个加薪方案,要求他从中选择:
方案一:是12个月后,在年薪20000元的基础上每年提高500元(第一年年薪20000元);
方案二:是6个月后,在半年薪10000元的基础上每半年提高250元(第6个月末发薪水10000元)
但不管是选哪一种方案,公司都是每半年发一次工资,如果你是工会代言人,认为哪种方案对员工更有利?( )
A.方案一
B.方案二
C.两种方案一样
D.工龄短的选方案一,工龄长的选方案二
3.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用(元)
每次游泳收费(元)
A
类
50
25
B
类
200
20
C
类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为( )
A.购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
4.如图,购买一种苹果所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )
A.4元
B.3元
C.2元
D.1元
5.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示,下列结论正确的是( )
A.降价后西瓜的单价为2元/千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
6.某电信公司有A、B两种计费方案:月通话费用y(元)与通话时间x(分钟)的关系,如图所示,下列说法中正确的是( )
A.月通话时间低于200分钟选B方案划算
B.月通话时间超过300分钟且少于400分钟选A方案划算
C.月通话费用为70元时,A方案比B方案的通话时间长
D.月通话时间在400分钟内,B方案通话费用始终是50元
7.小卖部从批发市场购进一批杨梅,在销售了部分杨梅之后,余下的每千克降价3元,直至全部售完.销售金额y元与杨梅销售量x千克之间的关系如图所示.若销售这批杨梅一共赢利220元,那么这批杨梅的进价是( )
A.10元/千克
B.12元/千克
C.12.5元/千克
D.14.4元/千克
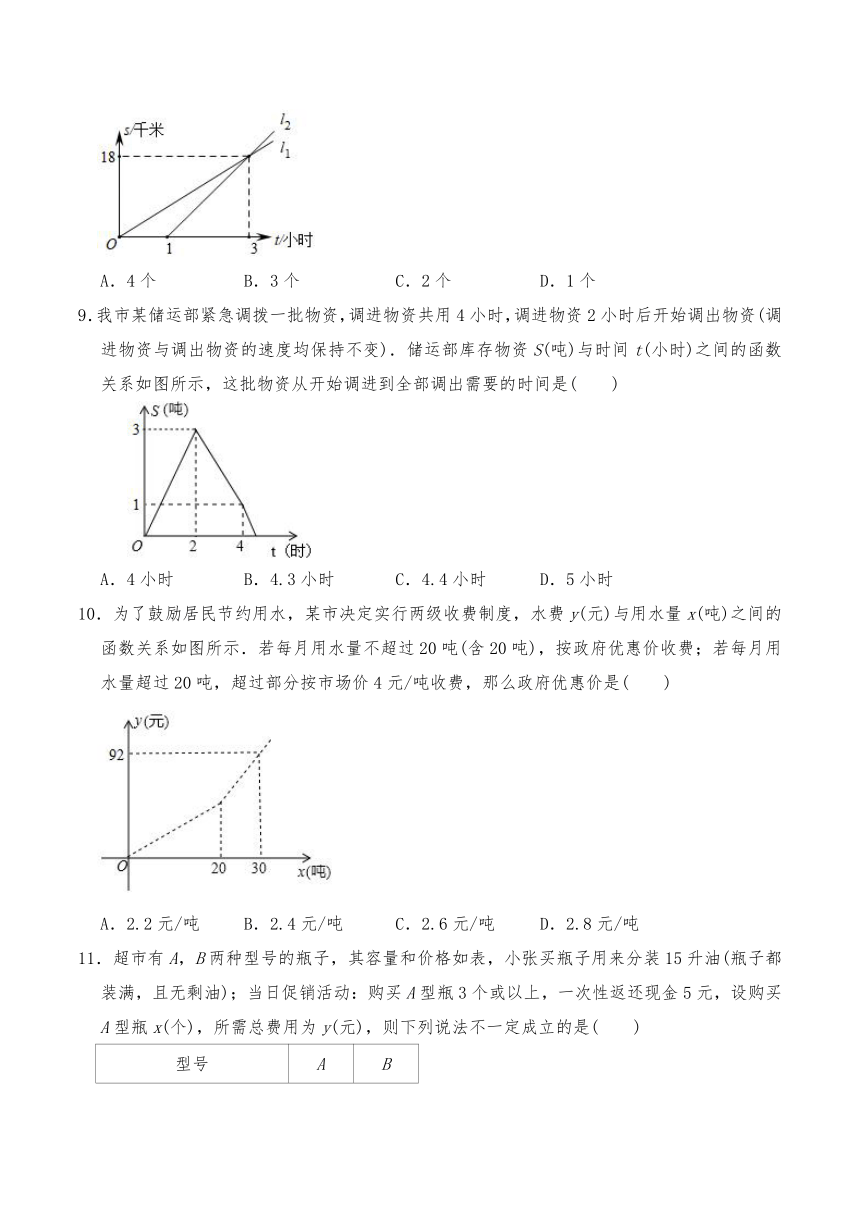
8.A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.对于下列说法:
①乙晚出发1小时:②乙出发3小时后追上甲;
③甲的速度是6千米/小时;④乙先到达B地.其中正确的个数是( )
A.4个
B.3个
C.2个
D.1个
9.我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
A.4小时
B.4.3小时
C.4.4小时
D.5小时
10.为了鼓励居民节约用水,某市决定实行两级收费制度,水费y(元)与用水量x(吨)之间的函数关系如图所示.若每月用水量不超过20吨(含20吨),按政府优惠价收费;若每月用水量超过20吨,超过部分按市场价4元/吨收费,那么政府优惠价是( )
A.2.2元/吨
B.2.4元/吨
C.2.6元/吨
D.2.8元/吨
11.超市有A,B两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买A型瓶3个或以上,一次性返还现金5元,设购买A型瓶x(个),所需总费用为y(元),则下列说法不一定成立的是( )
型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
A.购买B型瓶的个数是(5x)为正整数时的值
B.购买A型瓶最多为6个
C.y与x之间的函数关系式为y=x+30
D.小张买瓶子的最少费用是28元
二、填空题
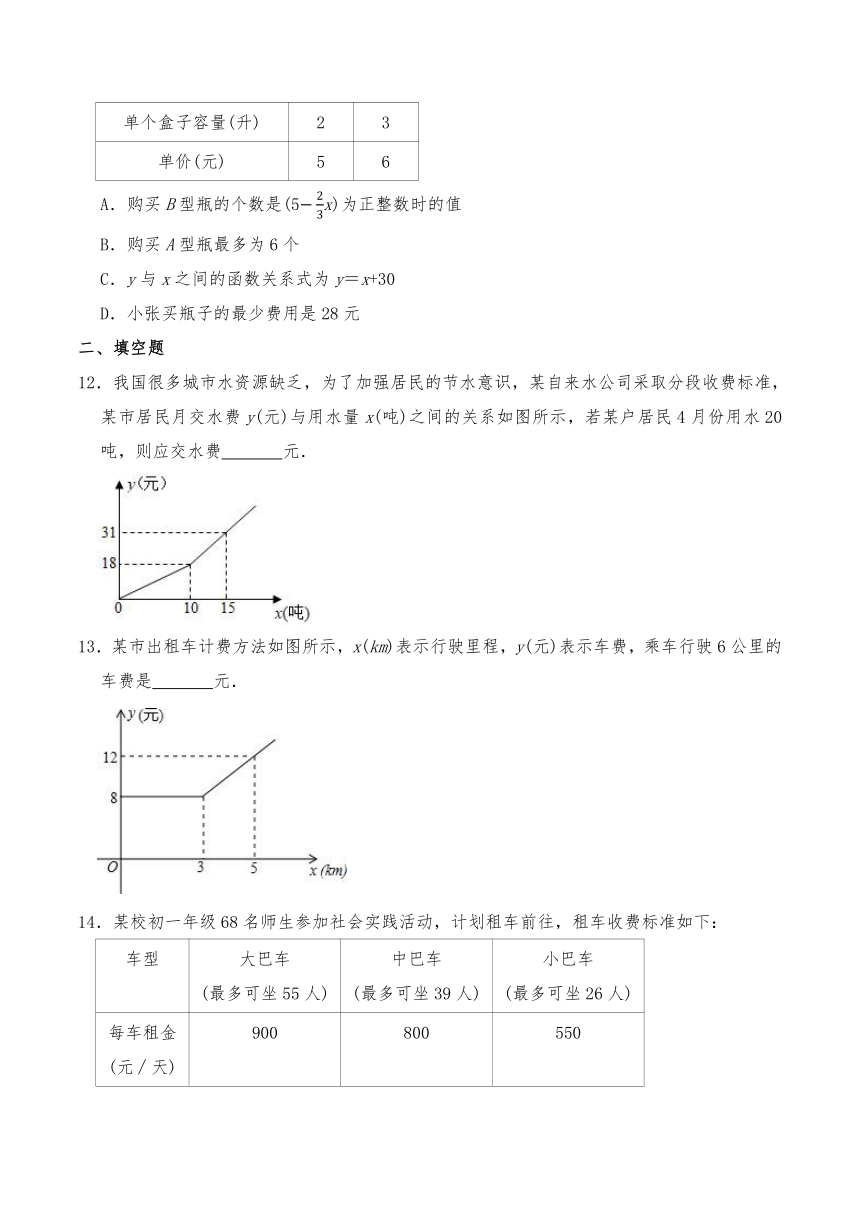
12.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费
元.
13.某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,乘车行驶6公里的车费是
元.
14.某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型
大巴车
(最多可坐55人)
中巴车
(最多可坐39人)
小巴车
(最多可坐26人)
每车租金
(元∕天)
900
800
550
则租车一天的最低费用为
元.
15.如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择
种业务合算.
16.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,如果班级搞一次茶话会,一次购买26千克这种苹果需
元.
17.某市政府大力扶持大学生创业.小甬在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数:y=﹣10x+500.根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果小甬想要每月获得的利润不低于2000元,那么他每月的成本最少需要
元.(成本=进价×销售量)
三、解答题
18.2017年“中国移动”公司提供两种通讯收费方案供客户选择.
根据以上信息,解答下列问题:
(1)设通话时间为x分钟,方案一的通讯费用为y1元,方案二的通讯费用为y2元,分别求出y1、y2关于x的函数表达式.
(2)请你通过计算说明如何选用通讯收费方案更合算.
(3)小明的爸爸每月的通话时间约为500分钟,应选用哪种通讯收费方案.
19.现有下面两种移动电话计费方式:
方式一
方式二
月租费/(元/月)
30
0
本地通话费/(元/min)
0.30
0.40
(1)以x(单位:分钟)表示通话时间,y(单位:元)表示通话费用,分别就两种移动电话计费方式写出y关于x的函数解析式;
(2)何时两种计费方式费用相等;
(3)直接写出如何选择这两种计费方式更省钱.
20.某工厂计划生产A、B两种产品共50件,已知A产品成本2000元/件,售价2300元/件;B种产品成本3000元/件,售价3500元/件,设该厂每天生产A种产品x件,两种产品全部售出后共可获利y元.
(1)求出y与x的函数表达式;
(2)如果该厂每天最多投入成本140000元,那么该厂生产的两种产品全部售出后最多能获利多少元?
21.某单位要印刷一批宣传材料,在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元;一次印刷页数超过20时,超过部分每页收费0.09元.设该单位需要印刷宣传材料的页数为x(x>20,且x为整数),在甲印刷厂实际付费为y1(元),在乙印刷厂实际付费为y2(元).
(1)分别求出y1,y2与x的函数关系式.
(2)你认为选择哪家印刷厂印刷这批宣传材料较好,为什么?
22.福州电信公司开设了A、B两种市内移动通信业务:A种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.1元:B种使用者不缴月租费,每通话1分钟,付话费0.3元,若一个月内通话时间为x分钟,A、B两种的费用分别为y1和y2元.
(1)试分别写出y1、y2与x之间的函数关系式;
(2)每月通话时间为多长时,开通A种业务和B种业务费用一样.
23.甲、乙两个药店销售同一种口罩,在甲药店,不论一次购买数量是多少,价格均为3元/个;在乙药店,一次性购买数量不超过100个时,价格为3.5元/个;一次性购买数量超过100个时,其中100个的价格仍为3.5元/个,超过100个的部分的价格为2.5元/个.
(1)根据题意填表:
一次性购买数量(个)
50
100
150
甲药店花费(元)
300
乙药店花费(元)
350
(2)当一次性购买多少个口罩时,在乙药店购买比在甲药店购买可以节约100元?
24.某图书借阅室提供两种租书方式:一种是零星租书,每册收费1元;另一种是会员租书,会员卡费用为每季度10元,租书费每册0.5元,小亮经常来租书,若每季度租书数量为x册.
(1)写出零星租书方式每季度应付金额y1(元)与租书数量x(册)之间的函数关系式;
(2)写出会员卡租书方式每季度应付金额y2(元)与租书数量x(册)之间的函数关系式;
(3)请分析小亮选取哪种租书方式更合算?
答案
一、选择题
1.D.2.B.3.C.4.C.5.C.6.D.7.A.8.B.9.C.10.C.11.C.
二、填空题
12.44.
13.14.
14.1450.
15.甲.
16..
17.3600.
三、解答题
18.(1)根据题意知,y1.
y2=0.2x(x≥0);
(2)当0≤x≤50时,y1=40>y2,选择方案二合算;
当x>50时:
①y1>y2,即0.1x+45>0.2x,
解得x<450,选择方案二合算;
②y1=y2,即0.1x+40=0.2x,
解得x=400,选择两种方案一样合算;
③y1<y2,即0.1x+40<0.2x,
解得x>450,选择方案一合算.
综上所述,当通话时间小于400分钟,选择方案二合算;当通话时间为400分钟,选择两种方案一样合算;当通话时间大于400分钟,选择方案一合算;
(3)由于500>400,所以小明的爸爸选用通讯收费方案一合算.
19.(1)由题意可得,
方式一中y关于x的函数解析式是y=0.30x+30,
方式二中y关于x的函数解析式是y=0.40x;
(2)令0.30x+30=0.40x,
解得,x=100,
即通话100分钟时两种计费方式费用相等;
(3)由(2)和表格中的数据可知,
当x>100时,选择方式一更省钱,
当x<100时,选择方式二更省钱,
当x=100时,两种方式一样.
20.(1)由题意可得,
y=(2300﹣2000)x+(3500﹣3000)(50﹣x)=﹣200x+25000,
即y与x的函数表达式为y=﹣200x+25000;
(2)∵该厂每天最多投入成本140000元,
∴2000x+3000(50﹣x)≤140000,
解得,x≥10,
∵y=﹣200x+25000,
∴当x=10时,y取得最大值,此时y=23000,
答:该厂生产的两种产品全部售出后最多能获利23000元.
21.(1)由题意得,y1=0.1x,y2=20×0.12+0.09(x﹣20)=0.09x+0.6,
∴y1,y2与x的函数关系式分别为y1=0.1x,y2=0.09x+0.6;
(2)当x>20时,
由y1<y2得,0.1x<0.09x+0.6,解得,x<60,
由y1=y2得,0.1x=0.09x+0.6,解得,x=60,
由y1>y2得
0.1x>0.09x+0.6,解得,x>60,
∴当x=60时,甲、乙两个印刷厂收费相同,当20<x<60时,甲印刷厂费用少,当x>60时,乙印刷厂费用少.
22.(1)由题意可得,
y1=0.1x+18(x≥0),
y2=0.3x(x≥0);
(2)令0.1x+18=0.3x,
解得:x=90,
答:每月通话时间为90分钟时,开通A种业务和B种业务费用一样.
23.(1)
故答案为:150,450,175,475;
(2)设购买x(x>100)个口罩时,在乙药店购买比在甲药店购买可以节约y元,根据题意得:
y=3x﹣[2.5(x﹣100)+3.5×100]=0.5x﹣100,
当y=100时,0.5x﹣100=100,解得x=400.
答:当一次性购买400个口罩时,在乙药店购买比在甲药店购买可以节约100元.
24.(1)∵零星租书每册收费1元,
∴零星租书方式每季度应付金额y1(元)与租书数量x(册)之间的函数关系式为:y1=x;
(2)∵在会员卡租书中,租书费每册0.5元,x册就是0.5x元,加上办卡费10元,
∴会员卡租书方式每季度应付金额y2(元)与租书数量x(册)之间的函数关系式为:y2=0.5x+10;
(3)当y1=y2时,x=10+0.5x,解得:x=20
当y1>y2时,x>10+0.5x,解得x>20
当y1<y2时,x<10+0.5x,解得x<20
综上所述,当小亮每季借书少于20册时,采用零星方式租书合算;当每季租书20册时,两种方式费用一样;当每季租书多于20册时,采用会员租书的方式更合算.
一、选择题
1.甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为xkg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元.y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5kg后,超过的部分价格优惠是打五折
D.若顾客采摘12kg草莓,那么到甲园或乙园的总费用相同
2.某公司为调动职工工作积极性,向工会代言人提供了两个加薪方案,要求他从中选择:
方案一:是12个月后,在年薪20000元的基础上每年提高500元(第一年年薪20000元);
方案二:是6个月后,在半年薪10000元的基础上每半年提高250元(第6个月末发薪水10000元)
但不管是选哪一种方案,公司都是每半年发一次工资,如果你是工会代言人,认为哪种方案对员工更有利?( )
A.方案一
B.方案二
C.两种方案一样
D.工龄短的选方案一,工龄长的选方案二
3.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用(元)
每次游泳收费(元)
A
类
50
25
B
类
200
20
C
类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为( )
A.购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
4.如图,购买一种苹果所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( )
A.4元
B.3元
C.2元
D.1元
5.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示,下列结论正确的是( )
A.降价后西瓜的单价为2元/千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
6.某电信公司有A、B两种计费方案:月通话费用y(元)与通话时间x(分钟)的关系,如图所示,下列说法中正确的是( )
A.月通话时间低于200分钟选B方案划算
B.月通话时间超过300分钟且少于400分钟选A方案划算
C.月通话费用为70元时,A方案比B方案的通话时间长
D.月通话时间在400分钟内,B方案通话费用始终是50元
7.小卖部从批发市场购进一批杨梅,在销售了部分杨梅之后,余下的每千克降价3元,直至全部售完.销售金额y元与杨梅销售量x千克之间的关系如图所示.若销售这批杨梅一共赢利220元,那么这批杨梅的进价是( )
A.10元/千克
B.12元/千克
C.12.5元/千克
D.14.4元/千克
8.A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.对于下列说法:
①乙晚出发1小时:②乙出发3小时后追上甲;
③甲的速度是6千米/小时;④乙先到达B地.其中正确的个数是( )
A.4个
B.3个
C.2个
D.1个
9.我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
A.4小时
B.4.3小时
C.4.4小时
D.5小时
10.为了鼓励居民节约用水,某市决定实行两级收费制度,水费y(元)与用水量x(吨)之间的函数关系如图所示.若每月用水量不超过20吨(含20吨),按政府优惠价收费;若每月用水量超过20吨,超过部分按市场价4元/吨收费,那么政府优惠价是( )
A.2.2元/吨
B.2.4元/吨
C.2.6元/吨
D.2.8元/吨
11.超市有A,B两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买A型瓶3个或以上,一次性返还现金5元,设购买A型瓶x(个),所需总费用为y(元),则下列说法不一定成立的是( )
型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
A.购买B型瓶的个数是(5x)为正整数时的值
B.购买A型瓶最多为6个
C.y与x之间的函数关系式为y=x+30
D.小张买瓶子的最少费用是28元
二、填空题
12.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费
元.
13.某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,乘车行驶6公里的车费是
元.
14.某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型
大巴车
(最多可坐55人)
中巴车
(最多可坐39人)
小巴车
(最多可坐26人)
每车租金
(元∕天)
900
800
550
则租车一天的最低费用为
元.
15.如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择
种业务合算.
16.如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,如果班级搞一次茶话会,一次购买26千克这种苹果需
元.
17.某市政府大力扶持大学生创业.小甬在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数:y=﹣10x+500.根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果小甬想要每月获得的利润不低于2000元,那么他每月的成本最少需要
元.(成本=进价×销售量)
三、解答题
18.2017年“中国移动”公司提供两种通讯收费方案供客户选择.
根据以上信息,解答下列问题:
(1)设通话时间为x分钟,方案一的通讯费用为y1元,方案二的通讯费用为y2元,分别求出y1、y2关于x的函数表达式.
(2)请你通过计算说明如何选用通讯收费方案更合算.
(3)小明的爸爸每月的通话时间约为500分钟,应选用哪种通讯收费方案.
19.现有下面两种移动电话计费方式:
方式一
方式二
月租费/(元/月)
30
0
本地通话费/(元/min)
0.30
0.40
(1)以x(单位:分钟)表示通话时间,y(单位:元)表示通话费用,分别就两种移动电话计费方式写出y关于x的函数解析式;
(2)何时两种计费方式费用相等;
(3)直接写出如何选择这两种计费方式更省钱.
20.某工厂计划生产A、B两种产品共50件,已知A产品成本2000元/件,售价2300元/件;B种产品成本3000元/件,售价3500元/件,设该厂每天生产A种产品x件,两种产品全部售出后共可获利y元.
(1)求出y与x的函数表达式;
(2)如果该厂每天最多投入成本140000元,那么该厂生产的两种产品全部售出后最多能获利多少元?
21.某单位要印刷一批宣传材料,在甲印刷厂不管一次印刷多少页,每页收费0.1元,在乙印刷厂,一次印刷页数不超过20时,每页收费0.12元;一次印刷页数超过20时,超过部分每页收费0.09元.设该单位需要印刷宣传材料的页数为x(x>20,且x为整数),在甲印刷厂实际付费为y1(元),在乙印刷厂实际付费为y2(元).
(1)分别求出y1,y2与x的函数关系式.
(2)你认为选择哪家印刷厂印刷这批宣传材料较好,为什么?
22.福州电信公司开设了A、B两种市内移动通信业务:A种使用者每月需缴18元月租费,然后每通话1分钟,再付话费0.1元:B种使用者不缴月租费,每通话1分钟,付话费0.3元,若一个月内通话时间为x分钟,A、B两种的费用分别为y1和y2元.
(1)试分别写出y1、y2与x之间的函数关系式;
(2)每月通话时间为多长时,开通A种业务和B种业务费用一样.
23.甲、乙两个药店销售同一种口罩,在甲药店,不论一次购买数量是多少,价格均为3元/个;在乙药店,一次性购买数量不超过100个时,价格为3.5元/个;一次性购买数量超过100个时,其中100个的价格仍为3.5元/个,超过100个的部分的价格为2.5元/个.
(1)根据题意填表:
一次性购买数量(个)
50
100
150
甲药店花费(元)
300
乙药店花费(元)
350
(2)当一次性购买多少个口罩时,在乙药店购买比在甲药店购买可以节约100元?
24.某图书借阅室提供两种租书方式:一种是零星租书,每册收费1元;另一种是会员租书,会员卡费用为每季度10元,租书费每册0.5元,小亮经常来租书,若每季度租书数量为x册.
(1)写出零星租书方式每季度应付金额y1(元)与租书数量x(册)之间的函数关系式;
(2)写出会员卡租书方式每季度应付金额y2(元)与租书数量x(册)之间的函数关系式;
(3)请分析小亮选取哪种租书方式更合算?
答案
一、选择题
1.D.2.B.3.C.4.C.5.C.6.D.7.A.8.B.9.C.10.C.11.C.
二、填空题
12.44.
13.14.
14.1450.
15.甲.
16..
17.3600.
三、解答题
18.(1)根据题意知,y1.
y2=0.2x(x≥0);
(2)当0≤x≤50时,y1=40>y2,选择方案二合算;
当x>50时:
①y1>y2,即0.1x+45>0.2x,
解得x<450,选择方案二合算;
②y1=y2,即0.1x+40=0.2x,
解得x=400,选择两种方案一样合算;
③y1<y2,即0.1x+40<0.2x,
解得x>450,选择方案一合算.
综上所述,当通话时间小于400分钟,选择方案二合算;当通话时间为400分钟,选择两种方案一样合算;当通话时间大于400分钟,选择方案一合算;
(3)由于500>400,所以小明的爸爸选用通讯收费方案一合算.
19.(1)由题意可得,
方式一中y关于x的函数解析式是y=0.30x+30,
方式二中y关于x的函数解析式是y=0.40x;
(2)令0.30x+30=0.40x,
解得,x=100,
即通话100分钟时两种计费方式费用相等;
(3)由(2)和表格中的数据可知,
当x>100时,选择方式一更省钱,
当x<100时,选择方式二更省钱,
当x=100时,两种方式一样.
20.(1)由题意可得,
y=(2300﹣2000)x+(3500﹣3000)(50﹣x)=﹣200x+25000,
即y与x的函数表达式为y=﹣200x+25000;
(2)∵该厂每天最多投入成本140000元,
∴2000x+3000(50﹣x)≤140000,
解得,x≥10,
∵y=﹣200x+25000,
∴当x=10时,y取得最大值,此时y=23000,
答:该厂生产的两种产品全部售出后最多能获利23000元.
21.(1)由题意得,y1=0.1x,y2=20×0.12+0.09(x﹣20)=0.09x+0.6,
∴y1,y2与x的函数关系式分别为y1=0.1x,y2=0.09x+0.6;
(2)当x>20时,
由y1<y2得,0.1x<0.09x+0.6,解得,x<60,
由y1=y2得,0.1x=0.09x+0.6,解得,x=60,
由y1>y2得
0.1x>0.09x+0.6,解得,x>60,
∴当x=60时,甲、乙两个印刷厂收费相同,当20<x<60时,甲印刷厂费用少,当x>60时,乙印刷厂费用少.
22.(1)由题意可得,
y1=0.1x+18(x≥0),
y2=0.3x(x≥0);
(2)令0.1x+18=0.3x,
解得:x=90,
答:每月通话时间为90分钟时,开通A种业务和B种业务费用一样.
23.(1)
故答案为:150,450,175,475;
(2)设购买x(x>100)个口罩时,在乙药店购买比在甲药店购买可以节约y元,根据题意得:
y=3x﹣[2.5(x﹣100)+3.5×100]=0.5x﹣100,
当y=100时,0.5x﹣100=100,解得x=400.
答:当一次性购买400个口罩时,在乙药店购买比在甲药店购买可以节约100元.
24.(1)∵零星租书每册收费1元,
∴零星租书方式每季度应付金额y1(元)与租书数量x(册)之间的函数关系式为:y1=x;
(2)∵在会员卡租书中,租书费每册0.5元,x册就是0.5x元,加上办卡费10元,
∴会员卡租书方式每季度应付金额y2(元)与租书数量x(册)之间的函数关系式为:y2=0.5x+10;
(3)当y1=y2时,x=10+0.5x,解得:x=20
当y1>y2时,x>10+0.5x,解得x>20
当y1<y2时,x<10+0.5x,解得x<20
综上所述,当小亮每季借书少于20册时,采用零星方式租书合算;当每季租书20册时,两种方式费用一样;当每季租书多于20册时,采用会员租书的方式更合算.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
