北师大版 八年级数学上册 试题 一课一练 6.4 数据的离散程度 (Word版 含答案)
文档属性
| 名称 | 北师大版 八年级数学上册 试题 一课一练 6.4 数据的离散程度 (Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 74.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-27 07:52:10 | ||
图片预览



文档简介
6.4《数据的离散程度》
一、选择题.
1.甲、乙、丙、丁四位男间学在中考体育前进行10次立定跳远测试,平均成绩都是2.4米.方差分别是S甲2=0.65.S乙2=055.S丙2=0.50.S丁2=0.45,则成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁
2.下列判断正确的是( )
A.数据3、5、4、﹣2、1的中位数为4
B.从初三体考成绩中抽取100名学生的体考成绩,这100名考生是总体的一个样本
C.甲乙两人各射靶5次,已知方差:0.8、0.4,那么乙的射击成绩稳定
D.了解云南省昆明市居民疫情期间的出行方式,应采用全面调查的方式
3.某中学举办了“校园文化节”活动,小颖同学在这次活动中参加了歌唱比赛,比赛由九位评委打分.小颖同学分析九位评委打的分数后,制成如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,那么表格中数据定不发生变化的是( )
A.平均数
B.中位数
C.众数
D.方差
4.在一场排球比赛中,某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.如果用一名身高为190cm的队员替换场上身高为184cm的队员,那么换人后与换人前相比,场上队员身高的平均数和方差大小变化正确的是( )
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
5.甲、乙、丙、丁四位同学五次数学测验的成绩的平均数相同,五次测验的方差如表.如果从四位同学中选出一位状态稳定的同学参加全国数学联赛,那么应选择( )
甲
乙
丙
丁
方差
4
2
55
19
A.甲
B.乙
C.丙
D.丁
6.某校合唱团有90名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁)
13
14
15
16
17
频数(单位:名)
17
29
x
26﹣x
18
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差
7.为了了解某校学生的课外阅读情况,随机抽查了10名学生一周阅读用时数,结果如下表:则关于这10名学生周阅读所用时间,下列说法正确的是( )
周阅读用时数(小时)
4
5
8
12
学生人数(人)
3
4
2
1
A.中位数是6.5
B.众数是12
C.平均数是3.9
D.方差是6
8.有一组统计数据:50、60、70、65、85、80、80.则对数据描述正确的是( )
A.中位数是65
B.平均数80
C.众数是80
D.方差是85
9.甲,乙,丙,丁四位同学本学期5次50米短跑成绩的平均数(秒)及方差S2如下表所示.若从这四位同学中选出一位成绩较好且状态稳定的同学参加学校比赛,则应该选的同学是( )
甲
乙
丙
丁
7
7
7.5
7.5
s2
0.45
0.2
0.2
0.45
A.甲
B.乙
C.丙
D.丁
10.对甲、乙、丙、丁四名选手进行射击比赛,每人射击10次,平均成绩均为9.5环,且他们的方差如下表所示.则在这四个选手中,成绩最稳定的是( )
选手
甲
乙
丙
丁
方差
1.56
0.60
2.50
0.40
A.甲
B.乙
C.丙
D.丁
二、填空题
11.甲、乙两篮球队队员身高的平均数都为2.08米,方差分别是S甲2、S乙2,且S甲2>S乙2,则队员身高比较整齐的球队是
.
12.甲,乙二人参加射击测试,两人10次射击的平均成绩均为8.5环,各自的方差如下表所示,则两人中射击成绩较稳定的是
.
人员
甲
乙
方差
0.6
2.8
13.如表记录了甲、乙、丙、丁四名同学最近五次数学考试成绩的平均分与方差:
甲
乙
丙
丁
平均分
93
96
96
93
方差(s2)
5.1
5.1
1.2
1.2
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择
.
14.若一组数据x1,x2,…,xn的平均数为5,方差为9,则数据2x1+3,2x2+3,…,2xn+3的平均数为
,方差为
.
15.在本学期的五次数学检测中,甲同学的成绩是:92,89,88,87,94,甲同学成绩的方差是
.
16.甲、乙、丙、丁四名运动员参加了射击预选赛,他们的成绩的平均环数及其方差s2如图表所示,如果选出一个成绩较好且状态稳定的人去参赛,那么应选
.
甲
乙
丙
丁
7
8
8
7
S2
1
1
1.2
1.8
17.学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他成绩的平均数及方差如表所示.请你根据上表中的数据选一人参加比赛,最适合的人选是
.
甲
乙
平均数(环)
9.5
9.5
方差
0.018
0.038
18.我们知道,方差是度量数据波动程度的量.此外,统计中还常用标准差来度量数据的波动程度,其中标准差s,已知一组数据x1,x2,x3,x4,x5的方差是3,则另一组新数据2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的标准差为
.
三、解答题
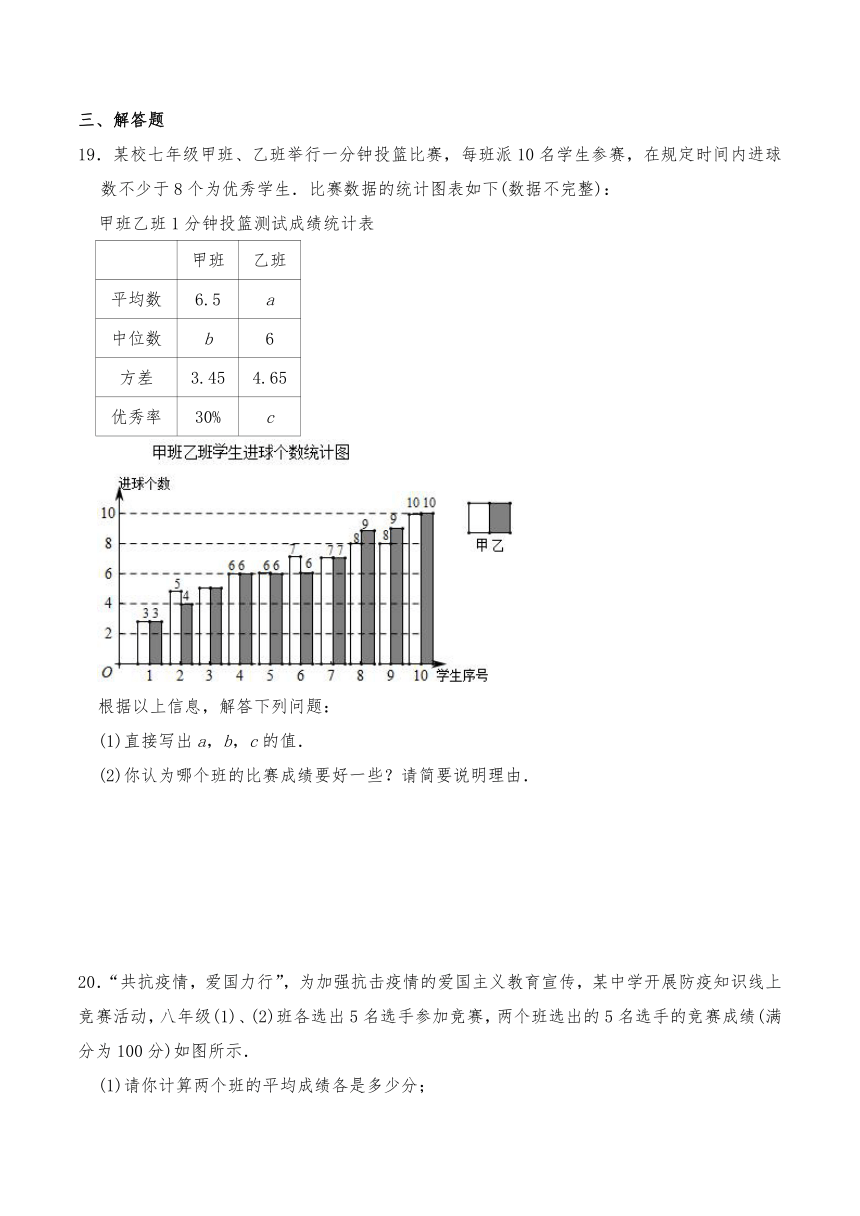
19.某校七年级甲班、乙班举行一分钟投篮比赛,每班派10名学生参赛,在规定时间内进球数不少于8个为优秀学生.比赛数据的统计图表如下(数据不完整):
甲班乙班1分钟投篮测试成绩统计表
甲班
乙班
平均数
6.5
a
中位数
b
6
方差
3.45
4.65
优秀率
30%
c
根据以上信息,解答下列问题:
(1)直接写出a,b,c的值.
(2)你认为哪个班的比赛成绩要好一些?请简要说明理由.
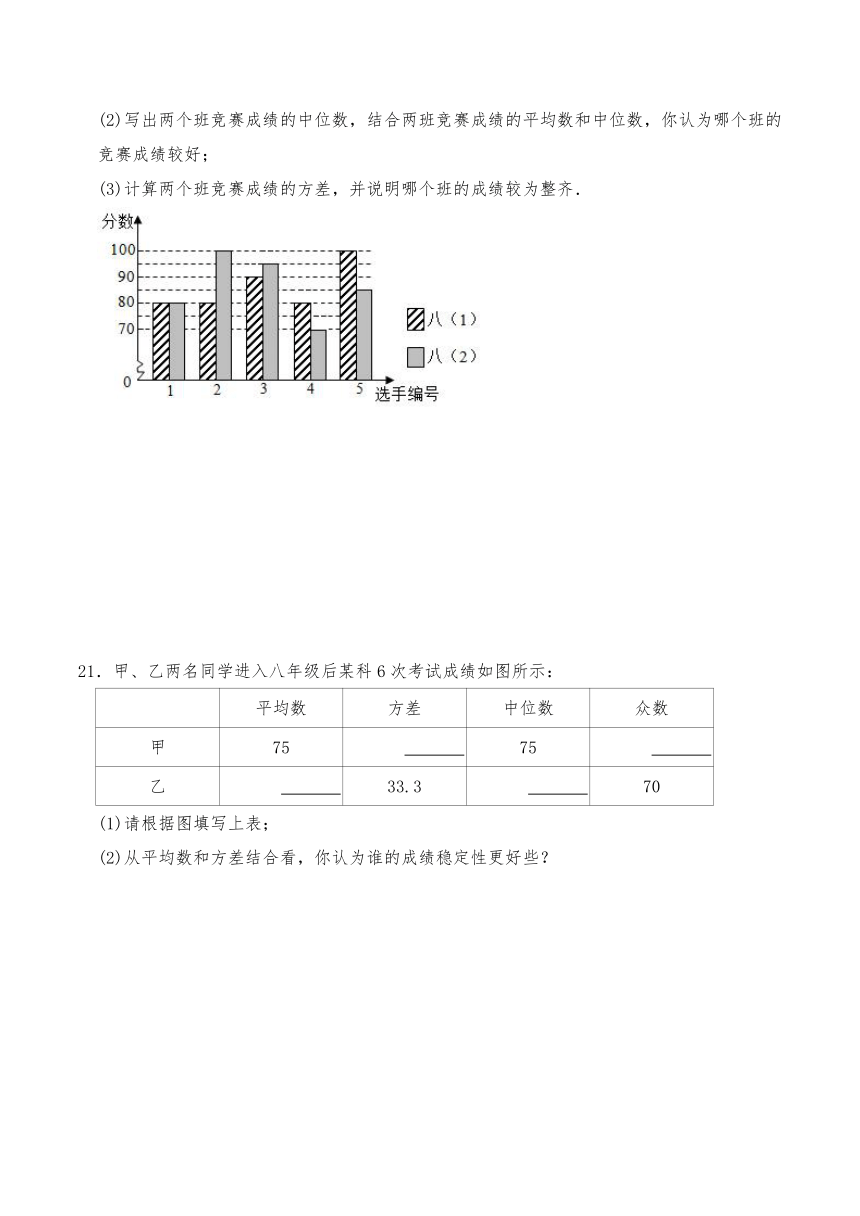
20.“共抗疫情,爱国力行”,为加强抗击疫情的爱国主义教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)请你计算两个班的平均成绩各是多少分;
(2)写出两个班竞赛成绩的中位数,结合两班竞赛成绩的平均数和中位数,你认为哪个班的竞赛成绩较好;
(3)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
21.甲、乙两名同学进入八年级后某科6次考试成绩如图所示:
平均数
方差
中位数
众数
甲
75
75
乙
33.3
70
(1)请根据图填写上表;
(2)从平均数和方差结合看,你认为谁的成绩稳定性更好些?
22.某球队从队员中选拔选手参加3分球大赛,对报名的两名选手进行3分球投篮测试,测试共五组,每组投10次,进球的个数统计结果如表:
队员
进球数(个/组)
一
二
三
四
五
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为8,方差为S甲2=3.2.
(1)求乙进球的平均数和方差S乙2;
(2)现从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
23.学校组织了“我和我的祖国”演讲比赛,甲、乙两队各有10人参加本次比赛,成绩(10分制)如下表所示.
甲
10
8
7
9
8
10
10
9
10
9
乙
7
8
9
7
10
10
9
10
10
10
(1)甲队成绩的众数是
分,乙队成绩的平均数是
分.
(2)问哪个队的成绩较为整齐?
24.2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情,为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传,某校为了了解初一年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试,现随机抽取甲、乙两班各1名同学的测试成绩进行整理分析,过程如下:
【收集数据】
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93
【整理数据】
班级
75≤x<80
80≤x<85
85≤x<90
90≤x<95
95≤x<100
甲
1
1
3
4
6
乙
1
2
3
5
4
【分析数据】
班级
平均数
众数
中位数
方差
甲
92
a
93
47.3
乙
90
87
b
50.2
【应用数据】
(1)根据以上信息,可以求出:a=
分,b=
分;
(2)若规定测试成绩90分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;
(3)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可).
答案
一、选择题
1.D.2.C.3.B.4.C.5.B.6.C.7.D.8.C.9.C.10.D.
二、填空题
11.乙.
12.甲.
13.丙.
14.13,36.
15.6.8.
16.乙.
17.甲.
18.2.
三、解答题
19.(1)甲班的3号同学进球的个数为:6.5×10﹣3﹣5﹣6﹣6﹣7﹣7﹣8﹣8﹣10=5(个),因此乙班3号同学进球个数也是5个,
a(3+4+5+6×3+7+9×2+10)=6.5,
甲班10名同学进球的个数从小到大排列后,处在中间位置的两个数的平均数为6.5,故中位数是6.5,即b=6.5,
c=3÷10=30%,
故a=6.5,b=6.5,c=30%;
(2)甲班的比赛成绩要好一些;
理由:甲班的中位数略高于乙班,方差小于乙班.
20.(1)八(1)班的平均成绩是:(80+80+90+80+100)=86(分);
八(2)班的平均成绩是:(80+100+90+95+85)=90(分);
(2)八(1)班的中位数是80分,八(2)班的中位数是90分,
∵八(1)班的平均成绩是86分,八(2)班的平均成绩是90分,八(1)班的中位数是80分,八(2)班的中位数是90分,
∴八年级(2)班竞赛成绩较好;
(3)八(1)班的成绩比较稳定,
理由:八(1)班的方差是:[(80﹣86)2+(80﹣86)2+(90﹣86)2+(80﹣86)2+(100﹣86)2]=64,
八(2)班的方差是:[(80﹣90)2+(100﹣90)2+(95﹣90)2+(70﹣90)2+(85﹣90)2]=130,
∵八(1)班的方差小于八(2)班的方差,
∴八(1)班的成绩比较稳定.
21.(1)乙的平均数:(85+70+70+75+70+80)=75分,
S[(60﹣75)2+(65﹣75)2+(75﹣75)2+(75﹣75)2+(80﹣75)2+(95﹣75)2]=125,
乙的中位数为:(70+75)÷2=72.5,甲的众数75,乙的众数为70,
填写表格如下::
平均数
方差
中位数
众数
甲
75
125
75
75
乙
75
33.3
72.5
70
故答案为:75,125,72,5,75;
(2)从平均数上看家、乙两人的成绩相同,但乙的方差较小,说明乙的成绩比较稳定,单从是否稳定上看,乙的成绩较稳定.
22.(1)(7+9+7+8+9)÷5=8(个),
S乙2[(7﹣8)2+(9﹣8)2+(7﹣7)2+(8﹣8)2+(9﹣8)2]=0.8;
(2)∵S甲2=3.2,S乙2=0.8,
∴S甲2>S乙2,
∴乙的波动小,投篮更稳定
∴应选乙去参加3分球投篮大赛.
23.(1)甲队成绩中出现次数最多的是10分,因此众数是10,
乙队的平均数为:9,
故答案为:10,9;
(2)甲队的平均数为:9,
甲队的方差为:[(7﹣9)2+2(8﹣9)2+4(10﹣9)2]=1;
乙队的方差为:[(7﹣9)2×2+(8﹣9)2+(10﹣9)2×5]=1.4;
∵1<1.4,
∴甲队比较整齐,
24.(1)∵100出现次数最多,
∴众数是100分,则a=100;
乙组15名学生测试成绩中,中位数是第8个数,
即出现在90≤x<95这一组中,故b=92(分);
故答案为:100,92;
(2)根据题意得:
480304(人),
答:成绩为优秀的学生共304人.
(3)∵甲班方差<乙班方差,即47.3<50.2,
∴甲班学生掌握防疫测试整体水平较好.
一、选择题.
1.甲、乙、丙、丁四位男间学在中考体育前进行10次立定跳远测试,平均成绩都是2.4米.方差分别是S甲2=0.65.S乙2=055.S丙2=0.50.S丁2=0.45,则成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁
2.下列判断正确的是( )
A.数据3、5、4、﹣2、1的中位数为4
B.从初三体考成绩中抽取100名学生的体考成绩,这100名考生是总体的一个样本
C.甲乙两人各射靶5次,已知方差:0.8、0.4,那么乙的射击成绩稳定
D.了解云南省昆明市居民疫情期间的出行方式,应采用全面调查的方式
3.某中学举办了“校园文化节”活动,小颖同学在这次活动中参加了歌唱比赛,比赛由九位评委打分.小颖同学分析九位评委打的分数后,制成如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,那么表格中数据定不发生变化的是( )
A.平均数
B.中位数
C.众数
D.方差
4.在一场排球比赛中,某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.如果用一名身高为190cm的队员替换场上身高为184cm的队员,那么换人后与换人前相比,场上队员身高的平均数和方差大小变化正确的是( )
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
5.甲、乙、丙、丁四位同学五次数学测验的成绩的平均数相同,五次测验的方差如表.如果从四位同学中选出一位状态稳定的同学参加全国数学联赛,那么应选择( )
甲
乙
丙
丁
方差
4
2
55
19
A.甲
B.乙
C.丙
D.丁
6.某校合唱团有90名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁)
13
14
15
16
17
频数(单位:名)
17
29
x
26﹣x
18
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差
7.为了了解某校学生的课外阅读情况,随机抽查了10名学生一周阅读用时数,结果如下表:则关于这10名学生周阅读所用时间,下列说法正确的是( )
周阅读用时数(小时)
4
5
8
12
学生人数(人)
3
4
2
1
A.中位数是6.5
B.众数是12
C.平均数是3.9
D.方差是6
8.有一组统计数据:50、60、70、65、85、80、80.则对数据描述正确的是( )
A.中位数是65
B.平均数80
C.众数是80
D.方差是85
9.甲,乙,丙,丁四位同学本学期5次50米短跑成绩的平均数(秒)及方差S2如下表所示.若从这四位同学中选出一位成绩较好且状态稳定的同学参加学校比赛,则应该选的同学是( )
甲
乙
丙
丁
7
7
7.5
7.5
s2
0.45
0.2
0.2
0.45
A.甲
B.乙
C.丙
D.丁
10.对甲、乙、丙、丁四名选手进行射击比赛,每人射击10次,平均成绩均为9.5环,且他们的方差如下表所示.则在这四个选手中,成绩最稳定的是( )
选手
甲
乙
丙
丁
方差
1.56
0.60
2.50
0.40
A.甲
B.乙
C.丙
D.丁
二、填空题
11.甲、乙两篮球队队员身高的平均数都为2.08米,方差分别是S甲2、S乙2,且S甲2>S乙2,则队员身高比较整齐的球队是
.
12.甲,乙二人参加射击测试,两人10次射击的平均成绩均为8.5环,各自的方差如下表所示,则两人中射击成绩较稳定的是
.
人员
甲
乙
方差
0.6
2.8
13.如表记录了甲、乙、丙、丁四名同学最近五次数学考试成绩的平均分与方差:
甲
乙
丙
丁
平均分
93
96
96
93
方差(s2)
5.1
5.1
1.2
1.2
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择
.
14.若一组数据x1,x2,…,xn的平均数为5,方差为9,则数据2x1+3,2x2+3,…,2xn+3的平均数为
,方差为
.
15.在本学期的五次数学检测中,甲同学的成绩是:92,89,88,87,94,甲同学成绩的方差是
.
16.甲、乙、丙、丁四名运动员参加了射击预选赛,他们的成绩的平均环数及其方差s2如图表所示,如果选出一个成绩较好且状态稳定的人去参赛,那么应选
.
甲
乙
丙
丁
7
8
8
7
S2
1
1
1.2
1.8
17.学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他成绩的平均数及方差如表所示.请你根据上表中的数据选一人参加比赛,最适合的人选是
.
甲
乙
平均数(环)
9.5
9.5
方差
0.018
0.038
18.我们知道,方差是度量数据波动程度的量.此外,统计中还常用标准差来度量数据的波动程度,其中标准差s,已知一组数据x1,x2,x3,x4,x5的方差是3,则另一组新数据2x1+1,2x2+1,2x3+1,2x4+1,2x5+1的标准差为
.
三、解答题
19.某校七年级甲班、乙班举行一分钟投篮比赛,每班派10名学生参赛,在规定时间内进球数不少于8个为优秀学生.比赛数据的统计图表如下(数据不完整):
甲班乙班1分钟投篮测试成绩统计表
甲班
乙班
平均数
6.5
a
中位数
b
6
方差
3.45
4.65
优秀率
30%
c
根据以上信息,解答下列问题:
(1)直接写出a,b,c的值.
(2)你认为哪个班的比赛成绩要好一些?请简要说明理由.
20.“共抗疫情,爱国力行”,为加强抗击疫情的爱国主义教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)请你计算两个班的平均成绩各是多少分;
(2)写出两个班竞赛成绩的中位数,结合两班竞赛成绩的平均数和中位数,你认为哪个班的竞赛成绩较好;
(3)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
21.甲、乙两名同学进入八年级后某科6次考试成绩如图所示:
平均数
方差
中位数
众数
甲
75
75
乙
33.3
70
(1)请根据图填写上表;
(2)从平均数和方差结合看,你认为谁的成绩稳定性更好些?
22.某球队从队员中选拔选手参加3分球大赛,对报名的两名选手进行3分球投篮测试,测试共五组,每组投10次,进球的个数统计结果如表:
队员
进球数(个/组)
一
二
三
四
五
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为8,方差为S甲2=3.2.
(1)求乙进球的平均数和方差S乙2;
(2)现从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
23.学校组织了“我和我的祖国”演讲比赛,甲、乙两队各有10人参加本次比赛,成绩(10分制)如下表所示.
甲
10
8
7
9
8
10
10
9
10
9
乙
7
8
9
7
10
10
9
10
10
10
(1)甲队成绩的众数是
分,乙队成绩的平均数是
分.
(2)问哪个队的成绩较为整齐?
24.2020年注定是不平凡的一年,新年伊始,一场突如其来的疫情席卷全国,全国人民万众一心,抗战疫情,为了早日取得抗疫的胜利,各级政府、各大新闻媒体都加大了对防疫知识的宣传,某校为了了解初一年级共480名同学对防疫知识的掌握情况,对他们进行了防疫知识测试,现随机抽取甲、乙两班各1名同学的测试成绩进行整理分析,过程如下:
【收集数据】
甲班15名学生测试成绩分别为:
78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
乙班15名学生测试成绩中90≤x<95的成绩如下:91,92,94,90,93
【整理数据】
班级
75≤x<80
80≤x<85
85≤x<90
90≤x<95
95≤x<100
甲
1
1
3
4
6
乙
1
2
3
5
4
【分析数据】
班级
平均数
众数
中位数
方差
甲
92
a
93
47.3
乙
90
87
b
50.2
【应用数据】
(1)根据以上信息,可以求出:a=
分,b=
分;
(2)若规定测试成绩90分及其以上为优秀,请估计参加防疫知识测试的480名学生中成绩为优秀的学生共有多少人;
(3)根据以上数据,你认为哪个班的学生防疫测试的整体成绩较好?请说明理由(一条理由即可).
答案
一、选择题
1.D.2.C.3.B.4.C.5.B.6.C.7.D.8.C.9.C.10.D.
二、填空题
11.乙.
12.甲.
13.丙.
14.13,36.
15.6.8.
16.乙.
17.甲.
18.2.
三、解答题
19.(1)甲班的3号同学进球的个数为:6.5×10﹣3﹣5﹣6﹣6﹣7﹣7﹣8﹣8﹣10=5(个),因此乙班3号同学进球个数也是5个,
a(3+4+5+6×3+7+9×2+10)=6.5,
甲班10名同学进球的个数从小到大排列后,处在中间位置的两个数的平均数为6.5,故中位数是6.5,即b=6.5,
c=3÷10=30%,
故a=6.5,b=6.5,c=30%;
(2)甲班的比赛成绩要好一些;
理由:甲班的中位数略高于乙班,方差小于乙班.
20.(1)八(1)班的平均成绩是:(80+80+90+80+100)=86(分);
八(2)班的平均成绩是:(80+100+90+95+85)=90(分);
(2)八(1)班的中位数是80分,八(2)班的中位数是90分,
∵八(1)班的平均成绩是86分,八(2)班的平均成绩是90分,八(1)班的中位数是80分,八(2)班的中位数是90分,
∴八年级(2)班竞赛成绩较好;
(3)八(1)班的成绩比较稳定,
理由:八(1)班的方差是:[(80﹣86)2+(80﹣86)2+(90﹣86)2+(80﹣86)2+(100﹣86)2]=64,
八(2)班的方差是:[(80﹣90)2+(100﹣90)2+(95﹣90)2+(70﹣90)2+(85﹣90)2]=130,
∵八(1)班的方差小于八(2)班的方差,
∴八(1)班的成绩比较稳定.
21.(1)乙的平均数:(85+70+70+75+70+80)=75分,
S[(60﹣75)2+(65﹣75)2+(75﹣75)2+(75﹣75)2+(80﹣75)2+(95﹣75)2]=125,
乙的中位数为:(70+75)÷2=72.5,甲的众数75,乙的众数为70,
填写表格如下::
平均数
方差
中位数
众数
甲
75
125
75
75
乙
75
33.3
72.5
70
故答案为:75,125,72,5,75;
(2)从平均数上看家、乙两人的成绩相同,但乙的方差较小,说明乙的成绩比较稳定,单从是否稳定上看,乙的成绩较稳定.
22.(1)(7+9+7+8+9)÷5=8(个),
S乙2[(7﹣8)2+(9﹣8)2+(7﹣7)2+(8﹣8)2+(9﹣8)2]=0.8;
(2)∵S甲2=3.2,S乙2=0.8,
∴S甲2>S乙2,
∴乙的波动小,投篮更稳定
∴应选乙去参加3分球投篮大赛.
23.(1)甲队成绩中出现次数最多的是10分,因此众数是10,
乙队的平均数为:9,
故答案为:10,9;
(2)甲队的平均数为:9,
甲队的方差为:[(7﹣9)2+2(8﹣9)2+4(10﹣9)2]=1;
乙队的方差为:[(7﹣9)2×2+(8﹣9)2+(10﹣9)2×5]=1.4;
∵1<1.4,
∴甲队比较整齐,
24.(1)∵100出现次数最多,
∴众数是100分,则a=100;
乙组15名学生测试成绩中,中位数是第8个数,
即出现在90≤x<95这一组中,故b=92(分);
故答案为:100,92;
(2)根据题意得:
480304(人),
答:成绩为优秀的学生共304人.
(3)∵甲班方差<乙班方差,即47.3<50.2,
∴甲班学生掌握防疫测试整体水平较好.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
