山东省淄博市临淄区2020-2021学年七年级下学期期中数学试题(Word版 含解析)
文档属性
| 名称 | 山东省淄博市临淄区2020-2021学年七年级下学期期中数学试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 380.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-26 07:42:06 | ||
图片预览



文档简介
山东省淄博市临淄区2020-2021学年七年级下学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法中正确的是(
)
A.通过多次试验得到某事件发生的频率等于这一事件发生的概率
B.某人前次掷出的硬币都是正面朝上,那么第次掷出的硬币反面朝上的概率一定大于正面朝上的概率
C.不确定事件的概率可能等于
D.试验估计结果与理论概率不一定一致
2.下列用消元法解二元一次方程组中,不正确的是(
)
A.由①得:
B.由①②得:
C.由①②得:
D.把①整体代入②得:
3.下列命题是真命题的是(
)
A.同旁内角互补
B.三角形的一个外角大于内角
C.三角形的一个外角等于它的两个内角之和
D.直角三角形的两锐角互余
4.在同一平面直角坐标系中,函数与的图象的交点坐标为(
)
A.
B.
C.
D.
5.若方程组的解满足,则等于( )
A.2018
B.2019
C.2020
D.2021
6.如果一个两位数的十位数字与个位数字之和为6,那么这样的两位数的个数是(
)
A.3
B.6
C.5
D.4
7.下列条件能判定直线l1∥l2的是(
)
A.∠2=∠3
B.∠1=∠3
C.∠4+∠5=180°
D.∠2=∠4
8.若将一副三角板按如图所示的方式放置,则下列结论不正确的是(
)
A.
B.如果,则有
C.如果,则有
D.如果,必有
9.有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是(
?)
A.
B.
C.
D.
10.已知今年甲的年龄比乙的年龄多12岁,4年后甲的年龄恰好是乙的年龄的2倍,则甲今年的年龄是(
)
A.20岁
B.16岁
C.15岁
D.12岁
11.如图,将一张长方形纸条折叠,如果∠1=130°,则,∠2=(
)
A.100°
B.130°
C.150°
D.80°
12.如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是( )
A.∠ABE=3∠D
B.∠ABE+∠D=90°
C.∠ABE+3∠D=180°
D.∠ABE=2∠D
二、填空题
13.请将命题“对顶角相等”改写为“如果……,那么……”的形式:________.
14.某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是__________.
15.若买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买4支圆珠笔、4本日记本需_____元.
16.已知直线,将一块含角的直角三角板按如图方式放置(),其中,两点分别落在直线,上,若,则的度数为_________.
17.已知方程组的解是.则方程组的解是__________.
三、解答题
18.小明准备完成题目:解方程组,发现系数“□”印刷不清楚.
(1)他把“□”猜成3,请你解此时的方程组.
(2)张老师说:你在(1)中猜错了,我看到该题的正确答案里有结论:,互为相反数.依此说法,问原题中的“□”是多少?
19.如图,的2倍与的和是,比大,且,.
(1)求和的度数;
(2)求的度数.
20.一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜.
(1)当x=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
21.在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:?
摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)
按表格数据格式,表中的=
;=
;
(2)
请估计:当次数s很大时,摸到白球的频率将会接近
?(精确到0.1);?
(3)请推算:摸到红球的概率是
?(精确到0.1).
22.如图所示,与相交于点,,与互补.
(1)试说明;
(2)若,,求的度数.
23.阅读材料:
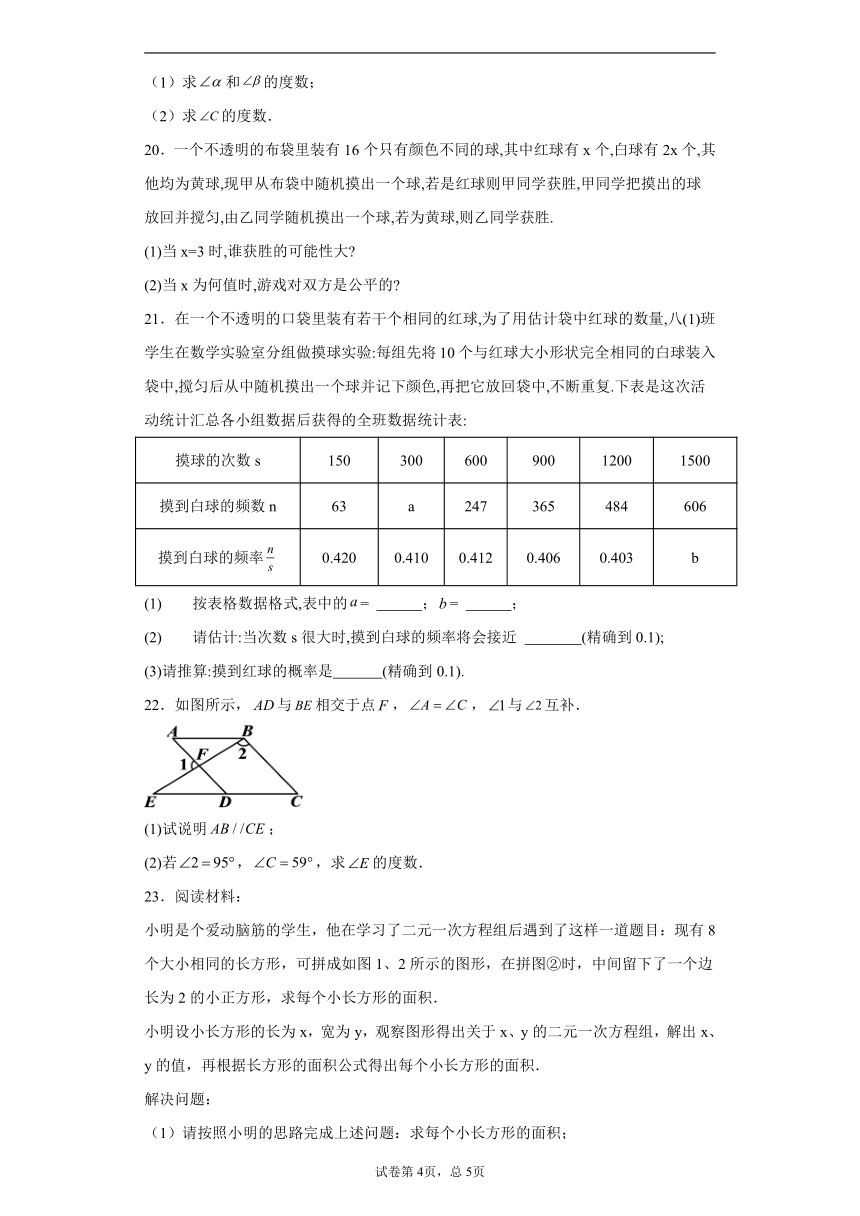
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是
cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
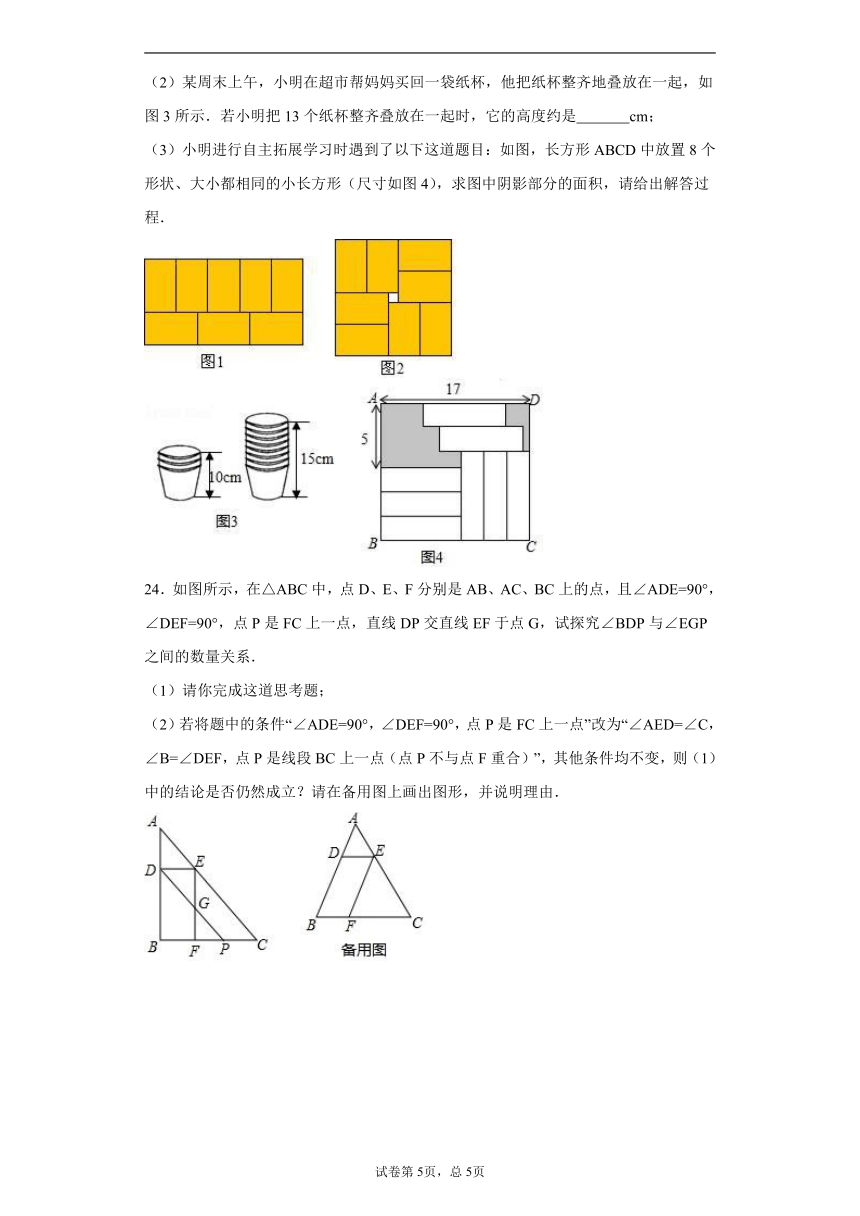
24.如图所示,在△ABC中,点D、E、F分别是AB、AC、BC上的点,且∠ADE=90°,∠DEF=90°,点P是FC上一点,直线DP交直线EF于点G,试探究∠BDP与∠EGP之间的数量关系.
(1)请你完成这道思考题;
(2)若将题中的条件“∠ADE=90°,∠DEF=90°,点P是FC上一点”改为“∠AED=∠C,∠B=∠DEF,点P是线段BC上一点(点P不与点F重合)”,其他条件均不变,则(1)中的结论是否仍然成立?请在备用图上画出图形,并说明理由.
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.D
【分析】
大量反复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值,而不是一种必然的结果,故选D.
【详解】
A.
错,应为:多次试验得到某事件发生的频率可以估计这一事件发生的概率;
B.
错,反面朝上的概率仍为0.5;
C.
错,概率等于1即为必然事件;
D.
正确.
故答案选D.
【点睛】
本题考查了概率的意义,解题的关键是熟练的掌握概率的意义.
2.B
【分析】
观察方程组中x与y的系数特点,利用消元法判断即可.
【详解】
解:A、由①得:,消去x,A正确;
B、由①②得,y=-3,B错误;
C、由①②得:,消去y,C正确;
D、把①整体代入②得:,D正确.
故选B.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
3.D
【分析】
分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【详解】
解:A.错误,两直线平行,同旁内角互补;
B.错误,三角形的一个外角不一定大于内角;
C.错误,三角形的一个外角等于与它不相邻的两个内角之和;
D.正确,直角三角形的两锐角互余,是真命题.
故选D.
【点睛】
主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
4.A
【分析】
令,求出x,代入任一表达式中,求出y值,可得坐标.
【详解】
解:令,
解得:x=-4,代入,
得:y=-4+5=1,
∴函数的交点为(-4,1),
故选A.
【点睛】
本题考查了一次函数的交点问题,解题的关键是令函数解析式相等求出x.
5.D
【分析】
把两个方程相加,可得5x+5y=5k-5,再根据可得到关于k的方程,进而求k即可.
【详解】
解:
①+②得
5x+5y=5k-5,
∴x+y=k-1.
∵,
∴k-1=2020,
∴k=2021.
故选:D.
【点睛】
本题考查了二元一次方程组的特殊解法,依据方程系数特点整体代入是求值的关键.
6.B
【详解】
设两位数的个位数为x,十位为y,根据题意得:
x+y=6,
∵x、y都是整数,
∴当x=0时,y=6,两位数为60;
当x=1时,y=5,两位数为51;
当x=2时,y=4,两位数为42;
当x=3时,y=3,两位数为33;
当x=4时,y=2,两位数为24;
当x=5时,y=1,两位数为15;
则此两位数可以为:60、51、42、33、24、15,共6个,
故选B.
7.B
【分析】
要证明两直线平行,则要找到同位角、内错角相等,同旁内角互补等.
【详解】
解:A、∠2和∠3不是直线l1、l2被第三条直线所截形成的角,故不能判断直线l1∥l2.
B、∵∠1=∠3,∴l1∥l2(同位角相等两直线平行).
C、∠4、∠5是直线l1、l2被第三条直线所截形成的同位角,故∠4+∠5=180°不能判断直线l1∥l2.
D、∠2、∠4是直线l1、l2被第三条直线所截形成的同旁内角,故∠2=∠4不能判断直线l1∥l2.
故选:B.
【点睛】
本题考查了平行线的判定定理,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.
8.C
【分析】
根据两种三角板的各角的度数,利用平行线的判定与性质结合已知条件对各个结论逐一验证,即可得出答案.
【详解】
解:A、∵∠CAB=∠EAD=90°,
∴∠1=∠CAB?∠2,∠3=∠EAD?∠2,
∴∠1=∠3;
故该选项正确,
B、∵∠2=30°,
∴∠1=90°?30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE;
故该选项正确,
C、∵∠2=30°,
∴∠3=90°?30°=60°,
∵∠B=45°,
∴BC不平行于AD;
故该选项错误;
D、由AC∥DE可得∠4=∠C;
故该选项正确,
故选:C.
【点睛】
此题主要考查了学生对平行线判定与性质、余角和补角的理解和掌握,解答此题时要明确两种三角板各角的度数.
9.C
【分析】
数出黑色瓷砖的数目和瓷砖总数,求出二者比值即可.
【详解】
解:根据题意分析可得:钥匙藏在黑色瓷砖下面的概率是黑色瓷砖面积与总面积的比值,进而转化为黑色瓷砖个
数与总数的比值即.
故选C.
【点睛】
本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
10.A
【分析】
设乙今年的年龄是x岁,则甲今年的年龄是(x+12)岁.根据等量关系:4年后甲的年龄恰好是乙的年龄的2倍,列出方程进行求解即可.
【详解】
设乙今年的年龄是x岁,
根据题意得:(x+12)+4=2(x+4),
解得:x=8,
则:x+12=20,
即甲今年的年龄是20岁,
故选A.
【点睛】
本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.
11.A
【详解】
.故选A.
12.D
【分析】
延长CD和BF交于点G,由AB∥CD可得∠CGB=∠ABG,再根据BF∥DE可得∠CGB=∠CDE,则∠CDE=∠ABG,再根据平分,得=2∠ABG,故可得到与∠CDE的关系.
【详解】
延长CD和BF交于点G,
∵AB∥CD
∴∠CGB=∠ABG,
∵BF∥DE
∴∠CGB=∠CDE,
∴∠CDE=∠ABG,
又∵平分,
∴=2∠ABG,
∴=2∠CDE,
故选D.
【点睛】
此题主要考查平行线的性质,解题的关键是根据题意作出辅助线进行解答.
13.如果两个角是对顶角,那么这两个角相等
【分析】
命题中的条件是两个角是对顶角,放在“如果”的后面,结论是这两个角相等,应放在“那么”的后面.
【详解】
解:题设为:两个角是对顶角,结论为:这两个角相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么这两个角相等,
故答案为:如果两个角是对顶角,那么这两个角相等.
【点睛】
本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单.
14.
【详解】
分析:
根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
详解:
∵红灯亮30秒,黄灯亮3秒,绿灯亮42秒,
∴P(红灯亮)=,
故答案为.
点睛:本题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
15.12
【分析】
本题中因为买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买3支圆珠笔、3本日记本共需4+5=9元,即买1支圆珠笔1、1本日记本需9÷3=3元,所以买4支圆珠笔、4本日记本需4×3=12元.
【详解】
解:因为买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元.
所以买3支圆珠笔、3本日记本共需4+5=9元,即买1支圆珠笔1、1本日记本需9÷3=3元,
所以买4支圆珠笔、4本日记本需4×3=12元.
答:买4支圆珠笔、4本日记本需12元.
故答案为12.
【点睛】
此题可说是一道发散性的题目,既可利用方程组解决问题,也可通过适当的推理来解决问题.
16.50
【分析】
根据平行线的性质即可得到结论.
【详解】
解:∵直线m∥n,
∴∠2=∠ABC+∠1=30°+20°=50°,
故答案为:50.
【点睛】
本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
17.
【分析】
两个方程组除未知数不同外其余都相同,所以可用换元法进行解答.
【详解】
解:在方程组中,设x-1=a,y+2=b,
则变形为方程组,
解得,
故答案为:.
【点睛】
本题考查了二元一次方程组的解,这类题目的解题关键是灵活运用二元一次方程组的解法,观察题目特点灵活解题.
18.(1);(2)-3
【分析】
(1)根据加减消元法,即可求解;
(2)把,代入,得,进而求出y的值,即可求出“□”的值.
【详解】
(1),
得:,解得:,
把代入①得:,
∴方程组的解为;
(2)由,互为相反数,得,
∴,解得:,
∴.
设“□”为,则,解得:,
∴“□”为:-3.
【点睛】
本题主要考查解二元一次方程组,掌握加减消元法和代入消元法,是解题的关键.
19.(1)∠α=55°,∠β=125°;(2)35°
【分析】
(1)根据题意得到二元一次方程组,利用加减消元法解方程组即可.
(2)证明AB∥CD,利用平行线的性质即可解决问题.
【详解】
解:(1)由题意可得:,
解得:,
(2)∵∠α+∠β=55°+125°=180°,
∴AB∥CD,
∴∠C+∠CAB=180°,
∵AC⊥AE,
∴∠CAE=90°,
∴∠C=180°-90°-55°=35°.
【点睛】
本题考查平行线的判定和性质,二元一次方程组等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
20.(1)当x=3时,B同学获胜可能性大(2)当x=4时,游戏对双方是公平的
【分析】
(1)比较A、B两位同学的概率解答即可.
(2)根据游戏的公平性,列出方程解答即可.
【详解】
(1)A同学获胜可能性为,B同学获胜可能性为,因为<,当x=3时,B同学获胜可能性大.
(2)游戏对双方公平必须有:,解得x=4,所以当x=4时,游戏对双方是公平的.
【点睛】
本题主要考查随机事件的概率的概念.
21.(1)a=123,b=0.404;(2)0.4;(3)0.6.
【分析】
(1)根据频率=频数÷样本总数分别求得a、b的值即可;
(2)从表中的统计数据可知,摸到白球的频率稳定在0.4左右;
(3)摸到红球的概率为1-0.4=0.6;
【详解】
解:(1)a=300×0.41=123,b=606÷1500=0.404;
(2)当次数s很大时,摸到白球的频率将会接近0.4;
(3)摸到红球的概率是1-0.4=0.6;
【点睛】
此题考查利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.组成整体的几部分的概率之和为1.
22.(1)见解析;(2)∠E=26°
【分析】
(1)先由∠1=∠BFD得出∠BFD+∠2=180°,故可得出AD∥BC,故可得出∠ADE=∠C,据此可得出∠A=∠ADE,进而得出结论;
(2)直接根据三角形内角和的性质即可得出结论.
【详解】
(1)∵∠1=∠BFD,∠1+∠2=180°,
∴∠BFD+∠2=180°,
∴AD∥BC,
∴∠ADE=∠C,
∴∠A=∠ADE,
∴AB∥CE;
(2)∵∠2=95°,∠C=59°,∠E+∠2+∠C=180°
∴∠E=180°?95°?59°=26°.
【点睛】
本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.
23.(1)每个小长方形的面积为60;(2)小明把13个纸杯整齐叠放在一起时,它的高度约是20cm(3)46
【分析】
(1)设小长方形的长为x,宽为y,观察图形即可得出关于x、y的二元一次方程组,解之即可得出x、y的值,再根据长方形的面积公式即可得出每个小正方形的面积;
(2)通过理解题意可知本题存在两个等量关系,即单独一个纸杯的高度+3个纸杯叠放在一起比单独的一个纸杯增高的高度=9,单独一个纸杯的高度+8个纸杯叠放在一起比单独的一个纸杯增高的高度=14.根据这两个等量关系可列出方程组;
(3)设小长方形的面积为x,宽为y,根据长方形ABCD的长为17,宽的两种不同表达方式列出方程组求出小长方形的长和宽,进一步求出图中阴影部分的面积.
【详解】
(1)设小长方形的长为x,宽为y,
根据题意得:,解得:,
∴xy=10×6=60.
故每个小长方形的面积为60;
(2)设每两个纸杯叠放在一起比单独的一个纸杯增高xcm,单独一个纸杯的高度为ycm,
则,解得,
则12x+y=12×1+8=20.
即小明把13个纸杯整齐叠放在一起时,它的高度约是20cm.
(3)设小长方形的长为x,宽为y,
根据题意得,
解得,
∴S阴影=17×14﹣8×8×3=46.
【点睛】
此题考查了二元一次方程组的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
24.(1)∠BDP+∠EGP=180°;理由见解析;(2)结论不变;证明见解析.
【分析】
(1)结论:∠BDP+∠EGP=180°.证明AB∥EF即可.
(2)结论不变,证明AB∥EF即可.
【详解】
(1)结论:∠BDP+∠EGP=180°.
理由:∵∠ADE=∠DEF=90°,
∴AB∥EF,
∴∠BDP=∠DGE,
∵∠DGE+∠EGP=180°,
∴∠BDP+∠EGP=180°.
(2)结论不变.
画出的图形如图所示,
∵∠AED=∠C,
∴DE∥BC,
∴∠ADE=∠B,
∵∠B=∠DEF,
∴∠ADE=∠DEF,
∴AB∥EF,
∴∠BDG=∠DGE,
∵∠DGE+∠EGP=180°,
∴∠BDP+∠EGP=180°.
【点睛】
本题考查了三角形内角和定理,平行线的判定和性质等知识,解题的关键是熟练掌握基本知识.
答案第1页,总2页
答案第1页,总2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法中正确的是(
)
A.通过多次试验得到某事件发生的频率等于这一事件发生的概率
B.某人前次掷出的硬币都是正面朝上,那么第次掷出的硬币反面朝上的概率一定大于正面朝上的概率
C.不确定事件的概率可能等于
D.试验估计结果与理论概率不一定一致
2.下列用消元法解二元一次方程组中,不正确的是(
)
A.由①得:
B.由①②得:
C.由①②得:
D.把①整体代入②得:
3.下列命题是真命题的是(
)
A.同旁内角互补
B.三角形的一个外角大于内角
C.三角形的一个外角等于它的两个内角之和
D.直角三角形的两锐角互余
4.在同一平面直角坐标系中,函数与的图象的交点坐标为(
)
A.
B.
C.
D.
5.若方程组的解满足,则等于( )
A.2018
B.2019
C.2020
D.2021
6.如果一个两位数的十位数字与个位数字之和为6,那么这样的两位数的个数是(
)
A.3
B.6
C.5
D.4
7.下列条件能判定直线l1∥l2的是(
)
A.∠2=∠3
B.∠1=∠3
C.∠4+∠5=180°
D.∠2=∠4
8.若将一副三角板按如图所示的方式放置,则下列结论不正确的是(
)
A.
B.如果,则有
C.如果,则有
D.如果,必有
9.有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是(
?)
A.
B.
C.
D.
10.已知今年甲的年龄比乙的年龄多12岁,4年后甲的年龄恰好是乙的年龄的2倍,则甲今年的年龄是(
)
A.20岁
B.16岁
C.15岁
D.12岁
11.如图,将一张长方形纸条折叠,如果∠1=130°,则,∠2=(
)
A.100°
B.130°
C.150°
D.80°
12.如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是( )
A.∠ABE=3∠D
B.∠ABE+∠D=90°
C.∠ABE+3∠D=180°
D.∠ABE=2∠D
二、填空题
13.请将命题“对顶角相等”改写为“如果……,那么……”的形式:________.
14.某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是__________.
15.若买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买4支圆珠笔、4本日记本需_____元.
16.已知直线,将一块含角的直角三角板按如图方式放置(),其中,两点分别落在直线,上,若,则的度数为_________.
17.已知方程组的解是.则方程组的解是__________.
三、解答题
18.小明准备完成题目:解方程组,发现系数“□”印刷不清楚.
(1)他把“□”猜成3,请你解此时的方程组.
(2)张老师说:你在(1)中猜错了,我看到该题的正确答案里有结论:,互为相反数.依此说法,问原题中的“□”是多少?
19.如图,的2倍与的和是,比大,且,.
(1)求和的度数;
(2)求的度数.
20.一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜.
(1)当x=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
21.在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:?
摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)
按表格数据格式,表中的=
;=
;
(2)
请估计:当次数s很大时,摸到白球的频率将会接近
?(精确到0.1);?
(3)请推算:摸到红球的概率是
?(精确到0.1).
22.如图所示,与相交于点,,与互补.
(1)试说明;
(2)若,,求的度数.
23.阅读材料:
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是
cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
24.如图所示,在△ABC中,点D、E、F分别是AB、AC、BC上的点,且∠ADE=90°,∠DEF=90°,点P是FC上一点,直线DP交直线EF于点G,试探究∠BDP与∠EGP之间的数量关系.
(1)请你完成这道思考题;
(2)若将题中的条件“∠ADE=90°,∠DEF=90°,点P是FC上一点”改为“∠AED=∠C,∠B=∠DEF,点P是线段BC上一点(点P不与点F重合)”,其他条件均不变,则(1)中的结论是否仍然成立?请在备用图上画出图形,并说明理由.
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.D
【分析】
大量反复试验时,某事件发生的频率会稳定在某个常数的附近,这个常数就叫做事件概率的估计值,而不是一种必然的结果,故选D.
【详解】
A.
错,应为:多次试验得到某事件发生的频率可以估计这一事件发生的概率;
B.
错,反面朝上的概率仍为0.5;
C.
错,概率等于1即为必然事件;
D.
正确.
故答案选D.
【点睛】
本题考查了概率的意义,解题的关键是熟练的掌握概率的意义.
2.B
【分析】
观察方程组中x与y的系数特点,利用消元法判断即可.
【详解】
解:A、由①得:,消去x,A正确;
B、由①②得,y=-3,B错误;
C、由①②得:,消去y,C正确;
D、把①整体代入②得:,D正确.
故选B.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
3.D
【分析】
分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
【详解】
解:A.错误,两直线平行,同旁内角互补;
B.错误,三角形的一个外角不一定大于内角;
C.错误,三角形的一个外角等于与它不相邻的两个内角之和;
D.正确,直角三角形的两锐角互余,是真命题.
故选D.
【点睛】
主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
4.A
【分析】
令,求出x,代入任一表达式中,求出y值,可得坐标.
【详解】
解:令,
解得:x=-4,代入,
得:y=-4+5=1,
∴函数的交点为(-4,1),
故选A.
【点睛】
本题考查了一次函数的交点问题,解题的关键是令函数解析式相等求出x.
5.D
【分析】
把两个方程相加,可得5x+5y=5k-5,再根据可得到关于k的方程,进而求k即可.
【详解】
解:
①+②得
5x+5y=5k-5,
∴x+y=k-1.
∵,
∴k-1=2020,
∴k=2021.
故选:D.
【点睛】
本题考查了二元一次方程组的特殊解法,依据方程系数特点整体代入是求值的关键.
6.B
【详解】
设两位数的个位数为x,十位为y,根据题意得:
x+y=6,
∵x、y都是整数,
∴当x=0时,y=6,两位数为60;
当x=1时,y=5,两位数为51;
当x=2时,y=4,两位数为42;
当x=3时,y=3,两位数为33;
当x=4时,y=2,两位数为24;
当x=5时,y=1,两位数为15;
则此两位数可以为:60、51、42、33、24、15,共6个,
故选B.
7.B
【分析】
要证明两直线平行,则要找到同位角、内错角相等,同旁内角互补等.
【详解】
解:A、∠2和∠3不是直线l1、l2被第三条直线所截形成的角,故不能判断直线l1∥l2.
B、∵∠1=∠3,∴l1∥l2(同位角相等两直线平行).
C、∠4、∠5是直线l1、l2被第三条直线所截形成的同位角,故∠4+∠5=180°不能判断直线l1∥l2.
D、∠2、∠4是直线l1、l2被第三条直线所截形成的同旁内角,故∠2=∠4不能判断直线l1∥l2.
故选:B.
【点睛】
本题考查了平行线的判定定理,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.
8.C
【分析】
根据两种三角板的各角的度数,利用平行线的判定与性质结合已知条件对各个结论逐一验证,即可得出答案.
【详解】
解:A、∵∠CAB=∠EAD=90°,
∴∠1=∠CAB?∠2,∠3=∠EAD?∠2,
∴∠1=∠3;
故该选项正确,
B、∵∠2=30°,
∴∠1=90°?30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE;
故该选项正确,
C、∵∠2=30°,
∴∠3=90°?30°=60°,
∵∠B=45°,
∴BC不平行于AD;
故该选项错误;
D、由AC∥DE可得∠4=∠C;
故该选项正确,
故选:C.
【点睛】
此题主要考查了学生对平行线判定与性质、余角和补角的理解和掌握,解答此题时要明确两种三角板各角的度数.
9.C
【分析】
数出黑色瓷砖的数目和瓷砖总数,求出二者比值即可.
【详解】
解:根据题意分析可得:钥匙藏在黑色瓷砖下面的概率是黑色瓷砖面积与总面积的比值,进而转化为黑色瓷砖个
数与总数的比值即.
故选C.
【点睛】
本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
10.A
【分析】
设乙今年的年龄是x岁,则甲今年的年龄是(x+12)岁.根据等量关系:4年后甲的年龄恰好是乙的年龄的2倍,列出方程进行求解即可.
【详解】
设乙今年的年龄是x岁,
根据题意得:(x+12)+4=2(x+4),
解得:x=8,
则:x+12=20,
即甲今年的年龄是20岁,
故选A.
【点睛】
本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.
11.A
【详解】
.故选A.
12.D
【分析】
延长CD和BF交于点G,由AB∥CD可得∠CGB=∠ABG,再根据BF∥DE可得∠CGB=∠CDE,则∠CDE=∠ABG,再根据平分,得=2∠ABG,故可得到与∠CDE的关系.
【详解】
延长CD和BF交于点G,
∵AB∥CD
∴∠CGB=∠ABG,
∵BF∥DE
∴∠CGB=∠CDE,
∴∠CDE=∠ABG,
又∵平分,
∴=2∠ABG,
∴=2∠CDE,
故选D.
【点睛】
此题主要考查平行线的性质,解题的关键是根据题意作出辅助线进行解答.
13.如果两个角是对顶角,那么这两个角相等
【分析】
命题中的条件是两个角是对顶角,放在“如果”的后面,结论是这两个角相等,应放在“那么”的后面.
【详解】
解:题设为:两个角是对顶角,结论为:这两个角相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么这两个角相等,
故答案为:如果两个角是对顶角,那么这两个角相等.
【点睛】
本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单.
14.
【详解】
分析:
根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
详解:
∵红灯亮30秒,黄灯亮3秒,绿灯亮42秒,
∴P(红灯亮)=,
故答案为.
点睛:本题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
15.12
【分析】
本题中因为买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买3支圆珠笔、3本日记本共需4+5=9元,即买1支圆珠笔1、1本日记本需9÷3=3元,所以买4支圆珠笔、4本日记本需4×3=12元.
【详解】
解:因为买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元.
所以买3支圆珠笔、3本日记本共需4+5=9元,即买1支圆珠笔1、1本日记本需9÷3=3元,
所以买4支圆珠笔、4本日记本需4×3=12元.
答:买4支圆珠笔、4本日记本需12元.
故答案为12.
【点睛】
此题可说是一道发散性的题目,既可利用方程组解决问题,也可通过适当的推理来解决问题.
16.50
【分析】
根据平行线的性质即可得到结论.
【详解】
解:∵直线m∥n,
∴∠2=∠ABC+∠1=30°+20°=50°,
故答案为:50.
【点睛】
本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.
17.
【分析】
两个方程组除未知数不同外其余都相同,所以可用换元法进行解答.
【详解】
解:在方程组中,设x-1=a,y+2=b,
则变形为方程组,
解得,
故答案为:.
【点睛】
本题考查了二元一次方程组的解,这类题目的解题关键是灵活运用二元一次方程组的解法,观察题目特点灵活解题.
18.(1);(2)-3
【分析】
(1)根据加减消元法,即可求解;
(2)把,代入,得,进而求出y的值,即可求出“□”的值.
【详解】
(1),
得:,解得:,
把代入①得:,
∴方程组的解为;
(2)由,互为相反数,得,
∴,解得:,
∴.
设“□”为,则,解得:,
∴“□”为:-3.
【点睛】
本题主要考查解二元一次方程组,掌握加减消元法和代入消元法,是解题的关键.
19.(1)∠α=55°,∠β=125°;(2)35°
【分析】
(1)根据题意得到二元一次方程组,利用加减消元法解方程组即可.
(2)证明AB∥CD,利用平行线的性质即可解决问题.
【详解】
解:(1)由题意可得:,
解得:,
(2)∵∠α+∠β=55°+125°=180°,
∴AB∥CD,
∴∠C+∠CAB=180°,
∵AC⊥AE,
∴∠CAE=90°,
∴∠C=180°-90°-55°=35°.
【点睛】
本题考查平行线的判定和性质,二元一次方程组等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
20.(1)当x=3时,B同学获胜可能性大(2)当x=4时,游戏对双方是公平的
【分析】
(1)比较A、B两位同学的概率解答即可.
(2)根据游戏的公平性,列出方程解答即可.
【详解】
(1)A同学获胜可能性为,B同学获胜可能性为,因为<,当x=3时,B同学获胜可能性大.
(2)游戏对双方公平必须有:,解得x=4,所以当x=4时,游戏对双方是公平的.
【点睛】
本题主要考查随机事件的概率的概念.
21.(1)a=123,b=0.404;(2)0.4;(3)0.6.
【分析】
(1)根据频率=频数÷样本总数分别求得a、b的值即可;
(2)从表中的统计数据可知,摸到白球的频率稳定在0.4左右;
(3)摸到红球的概率为1-0.4=0.6;
【详解】
解:(1)a=300×0.41=123,b=606÷1500=0.404;
(2)当次数s很大时,摸到白球的频率将会接近0.4;
(3)摸到红球的概率是1-0.4=0.6;
【点睛】
此题考查利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.组成整体的几部分的概率之和为1.
22.(1)见解析;(2)∠E=26°
【分析】
(1)先由∠1=∠BFD得出∠BFD+∠2=180°,故可得出AD∥BC,故可得出∠ADE=∠C,据此可得出∠A=∠ADE,进而得出结论;
(2)直接根据三角形内角和的性质即可得出结论.
【详解】
(1)∵∠1=∠BFD,∠1+∠2=180°,
∴∠BFD+∠2=180°,
∴AD∥BC,
∴∠ADE=∠C,
∴∠A=∠ADE,
∴AB∥CE;
(2)∵∠2=95°,∠C=59°,∠E+∠2+∠C=180°
∴∠E=180°?95°?59°=26°.
【点睛】
本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.
23.(1)每个小长方形的面积为60;(2)小明把13个纸杯整齐叠放在一起时,它的高度约是20cm(3)46
【分析】
(1)设小长方形的长为x,宽为y,观察图形即可得出关于x、y的二元一次方程组,解之即可得出x、y的值,再根据长方形的面积公式即可得出每个小正方形的面积;
(2)通过理解题意可知本题存在两个等量关系,即单独一个纸杯的高度+3个纸杯叠放在一起比单独的一个纸杯增高的高度=9,单独一个纸杯的高度+8个纸杯叠放在一起比单独的一个纸杯增高的高度=14.根据这两个等量关系可列出方程组;
(3)设小长方形的面积为x,宽为y,根据长方形ABCD的长为17,宽的两种不同表达方式列出方程组求出小长方形的长和宽,进一步求出图中阴影部分的面积.
【详解】
(1)设小长方形的长为x,宽为y,
根据题意得:,解得:,
∴xy=10×6=60.
故每个小长方形的面积为60;
(2)设每两个纸杯叠放在一起比单独的一个纸杯增高xcm,单独一个纸杯的高度为ycm,
则,解得,
则12x+y=12×1+8=20.
即小明把13个纸杯整齐叠放在一起时,它的高度约是20cm.
(3)设小长方形的长为x,宽为y,
根据题意得,
解得,
∴S阴影=17×14﹣8×8×3=46.
【点睛】
此题考查了二元一次方程组的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.
24.(1)∠BDP+∠EGP=180°;理由见解析;(2)结论不变;证明见解析.
【分析】
(1)结论:∠BDP+∠EGP=180°.证明AB∥EF即可.
(2)结论不变,证明AB∥EF即可.
【详解】
(1)结论:∠BDP+∠EGP=180°.
理由:∵∠ADE=∠DEF=90°,
∴AB∥EF,
∴∠BDP=∠DGE,
∵∠DGE+∠EGP=180°,
∴∠BDP+∠EGP=180°.
(2)结论不变.
画出的图形如图所示,
∵∠AED=∠C,
∴DE∥BC,
∴∠ADE=∠B,
∵∠B=∠DEF,
∴∠ADE=∠DEF,
∴AB∥EF,
∴∠BDG=∠DGE,
∵∠DGE+∠EGP=180°,
∴∠BDP+∠EGP=180°.
【点睛】
本题考查了三角形内角和定理,平行线的判定和性质等知识,解题的关键是熟练掌握基本知识.
答案第1页,总2页
答案第1页,总2页
同课章节目录
